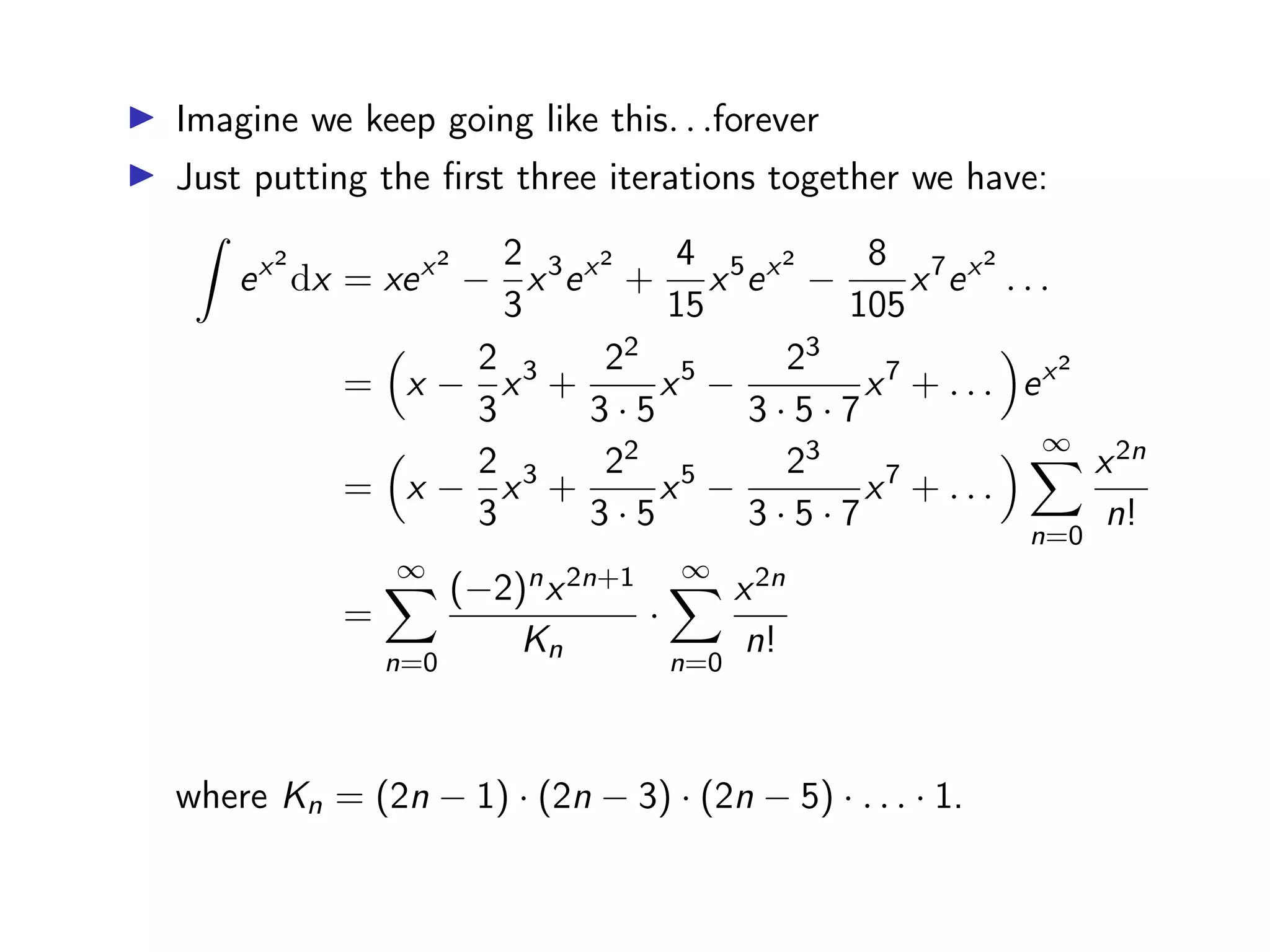This document provides definitions and examples of Taylor and Maclaurin series. It defines Taylor series as the power series representation of a function f(x) centered at a, and Maclaurin series as the special case where a = 0. It describes how to compute the coefficients of the series by taking derivatives of f(x) and evaluating them at the center point a. Examples show how to derive Taylor/Maclaurin series for common functions like ex, sinx, and ln(x+1). The document also discusses when a function is equal to its Taylor series based on the limit of the remainder terms.

1. Chapter 11: Sequences, Series, and Power Series
Section 11.10: Taylor and Maclaurin Series
Alea Wittig
SUNY Albany

2. Outline
Definitions of Taylor and Maclaurin Series
Examples
When is a Function Represented by its Taylor Series?
New Taylor Series from Old

3. Definitions of Taylor and Maclaurin Series

4. ▶ Suppose that we know that a given function f (x) has a power
series representation
f (x) =
∞
X
n=0
cn(x − a)n
|x − a| < R
but we don’t know the coefficients cn.
▶ How do we compute cn?
▶ f (x) = c0 + c1(x − a) + c2(x − a)2
+ . . . so if we plug in x = a
then we can find c0:
f (a) = c0 + c1(a − a) + c2(a − a)2
+ . . .
= c0 + 0 + 0 + . . .
= c0
ie, c0 = f (a).

5. ▶ In general, to find coefficient cn we can find a formula for the
nth derivative of the function using the theorem from 11.9:
f (x) = c0 + c1(x − a) + c2(x − a)2
+ . . .
f ′
(x) = c1 + 2c2(x − a) + 3c3(x − a)2
+ . . .
f ′′
(x) = 2c2 + 3 · 2c3(x − a) + 4 · 3c4(x − a)2
+ . . .
f ′′′
(x) = 3 · 2c3 + 4 · 3 · 2c4(x − a) + 5 · 4 · 3 · c5(x − a)2
. . .
.
.
.
f (n)
(x) = n!cn + (n + 1)!cn+1(x − a) + (n + 2)!cn+2(x − a)2
+ . . .
for |x − a| < R.
▶ And then plug in x = a

6. ▶ Plugging x = a into the formula:
f (n)
(x) = n!cn + (n + 1)!cn+1(x − a) + (n + 2)!cn+2(x − a)2
+ . . .
f (n)
(a) = n!cn
▶ Solving for cn then we have
cn =
f (n)(a)
n!

7. Theorem 5
▶ Theorem 5: If f has a power series expansion at a, that is
f (x) =
∞
X
n=0
cn(x − a)n
|x − a| < R
then its coefficients are given by
cn =
f (n)(a)
n!
▶ In other words, if f has a power series expansion at a then it
must have the following form:
f (x) =
∞
X
n=0
f (n)(a)
n!
(x − a)n
|x − a| < R
= f (a) +
f ′(a)
1!
(x − a) +
f ′′(a)
2!
(x − a)2
+ . . . |x − a| < R

8. Definition of Taylor Series and Maclaurin Series
▶ The series
∞
X
n=0
f (n)(a)
n!
(x − a)n
is called the Taylor series
of f at a.
▶ The special case when a = 0 is called the
Maclaurin series of f :
∞
X
n=0
f (n)(0)
n!
xn
= f (0) +
f ′(0)
1!
x +
f ′′(0)
2!
x2
+ . . .

9. Remark
▶ It is not always guaranteed that f (x) is equal to the sum of its
Taylor series because not all functions have a power series
representation at a.
▶ Nonetheless, we can compute the Taylor series of any
differentiable function by using the theorem and formula above.

10. Examples

11. Example 1
1/
Find the Maclaurin series for the function
f (x) =
1
1 − x

12. Example 1
2/

13. Example 2
1/
Find the Maclaurin series and radius of convergence for the function
f (x) = ex

14. Example 2
2/
f ′
(x) = ex
f ′′
(x) = ex
.
.
.
f (n)
(x) = ex
=⇒
f (n)
(x) = e0
= 1 =⇒
∞
X
n=0
f (n)(0)
n!
xn
=
∞
X
n=0
xn
n!
Radius of convergence:
lim
n→∞

17. an+1
an

20. = lim
n→∞

23. xn+1
(n + 1)!
n!
xn

26. = lim
n→∞
x
n + 1
= 0

27. When is a Function Represented by its Taylor
Series?

28. Partial Sum of a Functions Taylor Series
nth
Degree Taylor Polynomial of f
▶ Recall that the sum of a series is equal to the limit of its
partial sums:
∞
X
n=0
an = lim
n→∞
n
X
i=1
ai
▶ We can use the nth partial sum as an estimate for the value of
the sum.
▶ We call the nth partial sum of the Taylor series the
nth-Degree Taylor polynomial of f at a:
Tn(x) =
n
X
i=0
f (i)(a)
i!
(x − a)i
lim
n→∞
Tn(x) =
∞
X
n=0
f (n)(a)
n!
(x − a)n

29. Partial Sum of a Functions Taylor Series
▶ When we use the nth-Degree Taylor polynomial of f at a
to approximate the value of f (x), we have remainder:
Rn(x)
| {z }
Remainder
= f (x) −
n
X
i=1
f (i)(a)
i!
(x − a)i
| {z }
nth Partial Sum
= f (x) − Tn(x)
lim
n→∞
Rn(x) = f (x) − lim
n→∞
Tn(x)
= f (x) −
∞
X
n=0
f (n)(a)
n!
(x − a)n
▶ Therefore, if lim
n→∞
Rn(x) = 0, then f (x) =
∞
X
n=0
f (n)(a)
n!
(x − a)n
,
ie, f (x) is equal to its Taylor series.

30. Theorem 8
When is a function equal to its Taylor series?
▶ If the limit of the remainder Rn(x) is zero, then the function is
equal to its Taylor Series.
▶ In notation:
lim
n→∞
Rn(x) = 0 for |x − a| < R =⇒
f (x) =
∞
X
n=0
f (n)(a)
n!
(x − a)n
for |x − a| < R

31. Taylors Inequality
To show that lim
n→∞
Rn(x) = 0, we often use the following theorem:
Taylor’s Inequality
If |f (n+1)(x)| ≤ M for |x − a| ≤ d, then the remainder Rn(x) of the
Taylor series satisfies the inequality
Rn(x) ≤
M
(n + 1)!
|x − a|n+1
for |x − a| ≤ d

32. Theorem 10
▶ And we may also use the following theorem:
lim
n→∞
xn
n!
= 0 for every real number x (10)
▶ Sketch of Proof:
▶ Show that the series
P∞
n=0
xn
n! converges for all x using the
ratio test.
▶ Theorem 6 of 11.2, ie, the test for divergence, then implies the
sequence xn
n! must go to 0 as n → ∞.

33. Example 3
1/4
Prove that f (x) = ex is equal to its Maclaurin series.

34. Example 3
2/4
▶ First let’s write the Maclaurin series
∞
X
n=0
f (n)(0)
n!
xn
of ex .
▶ We need to find a formula for f (n)(0):
f (x) = ex
f ′
(x) = ex
f ′′
(x) = ex
.
.
.
f (n)
(x) = ex
=⇒
f n
(0) = e0
= 1
▶ So the Maclaurin series of ex is
∞
X
n=0
xn
n!

35. Example 3
3/4
▶ To show that ex is equal to its Maclaurin series, we need to
show that the limit of the remainder is 0:
lim
n→∞
Rn(x) = 0
▶ We will use Taylor’s Inequality to get a bound on Rn(x):
▶ Let d be any positive number.
|x| ≤ d =⇒ e|x|
≤ ed
=⇒ ex
≤ ed
▶ So since |f (n+1)
(x)| = ex
, letting M = ed
,
|f (n+1)(x)
| ≤ M for |x| ≤ d
▶ Taylor’s Inequality then tells us
Rn(x) ≤
ed
(n + 1)!
|x|n+1
for |x| ≤ d

36. Example 3
4/4
lim
n→∞
ed
(n + 1)!
|x|n+1
= ed
lim
n→∞
|x|n
n!
= 0 by theorem 10 above
▶ Now since 0 ≤ |Rn(x)| ≤
ed
(n + 1)!
|x|n+1
, we have
lim
n→∞
|Rn(x)| = 0 by squeeze theorem
▶ Which implies
lim
n→∞
Rn(x) = 0 by theorem 6 of 11.1 lecture notes
lim |an| = 0 =⇒ lim an = 0
▶ So we conclude that ex is equal to its Maclaurin series, ie,
ex
=
∞
X
n=0
xn
n!
for all x

38. ▶ Using Taylor’s inequality and theorem 10 we can prove that
sin x, cos x, ln (x + 1), 1
1−x , and tan−1 x are equal to their
Maclaurin series as well.
▶ Notice that for ex , sin x, cos x, ln (x + 1), and 1
1−x we can
write a formula for f (n)(0) fairly easily using the cyclical or
predictable nature of their derivatives.
sin x → cos x → − sin x → − cos x → sin x
cos x → − sin x → − cos x → sin x → cos x
ex
→ ex
→ ex
→ ex
→ . . .
ln (x + 1) →
1
x + 1
→ −
1
(x + 1)2
→
2
(x + 1)3
→ −
3 · 2
(x + 1)4
→ . . .
1
1 − x
→
1
(1 − x)2
→
2
(1 − x)3
→
3 · 2
(1 − x)4
→ . . .

39. Table of Important MacLaurin Series
1
1 − x
∞
X
n=0
xn
1 + x2 + x3 + . . . R = 1
ex
∞
X
n=0
xn
n!
1 +
x
1!
+
x2
2!
+
x3
3!
+ . . . R = ∞
sin x
∞
X
n=0
(−1)n x2n+1
(2n + 1)!
x −
x3
3!
+
x5
5!
−
x7
6!
+ . . . R = ∞
cos x
∞
X
n=0
(−1)n x2n
(2n)!
1 −
x2
2!
+
x4
4!
−
x6
6!
+ . . . R = ∞
tan−1 x
∞
X
n=0
(−1)n x2n+1
2n + 1
x −
x3
3
+
x5
5
−
x7
7
+ . . . R = 1
ln(x + 1)
∞
X
n=1
(−1)n−1 xn
n
x −
x2
2
+
x3
3
−
x4
4
+ . . . R = 1

40. New Taylor Series from Old

41. Example 5
1/3
Find the Maclaurin series for
(a) f (x) = x cos x
(b) f (x) = ln(1 + 3x2)

42. Example 5
2/3
(a) We know
cos x =
∞
X
n=0
(−1)n x2n
(2n)!
for all values of x. So multiplying both sides by x we have
x cos x = x
∞
X
n=0
(−1)n x2n
(2n)!
=
∞
X
n=0
(−1)n x2n+1
(2n)!
for all x

43. Example 5
3/3
(b) We know that
ln (1 + x) =
∞
X
n=0
(−1)n−1 xn
n
for |x| < 1
So plugging 3x2 in for x on both sides we get
ln(1 + 3x2
) =
∞
X
n=0
(−1)n−1 (3x2)n
n
=
∞
X
n=0
(−1)n−1 3n
n
x2n
for |3x2| < 1, ie, |x| < 1
√
3
.

44. Example 6
1/2
Find the function represented by the power series
∞
X
n=0
2nxn
n!

45. Example 6
2/2
▶ We can write
∞
X
n=0
2nxn
n!
=
∞
X
n=0
(2x)n
n!
▶ This looks like
ex
=
∞
X
n=0
xn
n!
but with 2x plugged in for x:
e2x
=
X
n=0
(2x)n
n!

46. Example 7
1/4
Find the sum of the series
1
1 · 2
−
1
2 · 22
+
1
3 · 23
−
1
4 · 24
+ . . .

47. Example 7
2/4
1
1 · 2
−
1
2 · 22
+
1
3 · 23
−
1
4 · 24
+ . . .
▶ Starting at n = 0 we have
a0 =
1
1 · 21
=
(−1)0
(0 + 1) · 20+1
a1 = −
1
2 · 22
=
(−1)1
(1 + 1) · 21+1
a2 =
1
3 · 23
=
(−1)2
(2 + 1) · 22+1
a3 =
1
4 · 24
=
(−1)3
(3 + 1) · 23+1
▶ So it appears that the pattern is an = (−1)n
(n+1)·2n+1

48. Example 7
3/4
▶ Let’s see if we can match this up with a known Maclaurin
series evaluated at some value of x.
∞
X
n=0
(−1)n
(n + 1) · 2n+1
=
∞
X
n=0
(−1)n
n + 1
1
2
n+1
=
∞
X
n=0
(−1)n
n + 1
xn+1
where x =
1
2

49. Example 7
4/4
▶
∞
X
n=0
(−1)n
n + 1
xn+1
looks similar to
ln (x + 1) =
∞
X
n=1
(−1)n−1 xn
n
for |x| 1
▶ Starting the index at n = 1 we can write
∞
X
n=0
(−1)n
n + 1
xn+1
=
∞
X
n=1
(−1)n−1
n
xn
= ln (x + 1)
=⇒
1
1 · 2
−
1
2 · 22
+
1
3 · 23
−
1
4 · 24
+. . . = ln (
1
2
+ 1) = ln
3
2

50. Example 8
1/3
Evaluate Z
ex2
dx

51. Example 8
2/3
▶ It was mentioned at the end of Chapter 7 that not all
elementary functions have elementary derivatives.
▶ The function f (x) = ex2
is an elementary function, as it is
made up of elementary functions ex and x2.
▶ Trying to integrate f (x) though is not possible without using
its power series.
ex
=
∞
X
n=0
xn
n!
for all x =⇒
ex2
=
∞
X
n=0
(x2)n
n!
for all x
=
∞
X
n=0
x2n
n!

52. Example 8
3/3
Z
ex2
dx =
Z ∞
X
n=0
x2n
n!
dx
= C +
∞
X
n=0
x2n+1
(2n + 1)n!
for all x
= C + x +
x3
3 · 1!
+
x5
5 · 2!
+ . . .

53. Just for Fun
▶ What if we had tried to use substitution?
s = x2, ds = 2xdx =⇒ dx = ds
2x = ds
2
√
s
Z
ex2
dx =
Z
es
2
√
s
ds
▶ Now use integration by parts
u = es dv = 1
2
√
s
ds
du = esds v =
√
s
#
Z
es
2
√
s
ds = es√
s −
Z
√
ses
ds

54. ▶ Integration by parts again:
u = es dv =
√
sds
du = esds v = 2s3/2
3
#
Z
√
ses
ds =
2ess3/2
3
−
Z
2s3/2
3
es
ds
▶ Again
u = es dv = 2s3/2
3 ds
du = esds v = 4s5/2
15
#
Z
2s3/2
3
es
ds =
4ess5/2
15
−
Z
4s5/2
15
es
ds

55. ▶ Imagine we keep going like this. . .forever
▶ Just putting the first three iterations together we have:
Z
ex2
dx = xex2
−
2
3
x3
ex2
+
4
15
x5
ex2
−
8
105
x7
ex2
. . .
=
x −
2
3
x3
+
22
3 · 5
x5
−
23
3 · 5 · 7
x7
+ . . .
ex2
=
x −
2
3
x3
+
22
3 · 5
x5
−
23
3 · 5 · 7
x7
+ . . .
∞
X
n=0
x2n
n!
=
∞
X
n=0
(−2)nx2n+1
Kn
·
∞
X
n=0
x2n
n!
where Kn = (2n − 1) · (2n − 3) · (2n − 5) · . . . · 1.