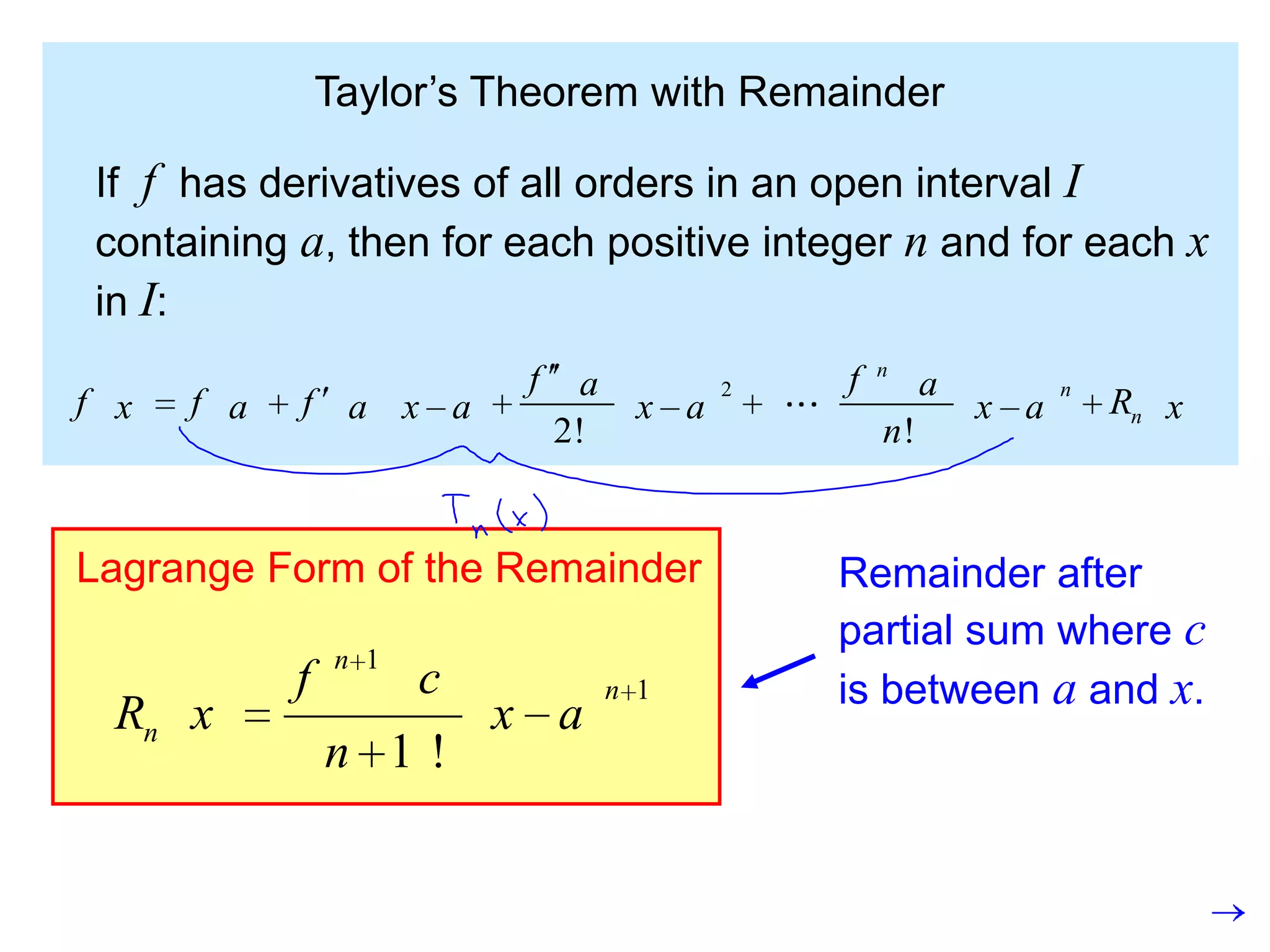
The document discusses using Taylor series to estimate the value of functions and introduces the Lagrange form of the remainder to determine the accuracy of estimates based on partial sums. It defines the Lagrange form of the remainder as the next term in the Taylor series with "a" replaced by a value "c" between the point "a" and the point "x" being estimated. The document also introduces the Remainder Estimation Theorem, which uses the maximum value of the derivative in the interval to bound the size of the remainder term.

1. Error Analysis for Series – Lagrange Form
Taylor series are used to estimate the value of functions (at
least theoretically - we can usually use the calculator or
computer to calculate directly.)
An estimate is only useful if we have an idea of how
accurate the estimate is.
When we use part of a Taylor series to estimate the value
of a function, the end of the series that we do not use is
called the remainder. If we know the size of the
remainder, then we know how close our estimate is.

2. Taylor’s Theorem with Remainder
If f has derivatives of all orders in an open interval I
containing a, then for each positive integer n and for each x
in I:
n
f a 2 f a n
f x f a f a x a x a x a Rn x
2! n!
Lagrange Form of the Remainder Remainder after
partial sum where c
n 1
f c n 1 is between a and x.
Rn x x a
n 1!

3. Lagrange Form of the Remainder Remainder after
partial sum Sn
n 1
f c n 1 where c is between
Rn x x a
n 1! a and x.
This is also called the remainder of order n or the error term.
Note that this looks just like the next term in the series, but
n 1
“a” has been replaced by the number “c” in f c .
This seems kind of vague, since we don’t know the value of
c, but we can sometimes find a maximum value for n 1
f c
.

4. Lagrange Form of the Remainder Note that some
n 1
books call this
f c n 1 Taylor’s Inequality
Rn x x a
n 1!
n 1
If K is the maximum value of f x on the interval
between a and x, then:
Remainder Estimation Theorem
We will call this the
K n 1 Remainder Estimation
Rn x x a
n 1! Theorem.

5. ex. 1: Find the Lagrange Error Bound for
where Tn(x) is the Taylor poly for ln 1 x at a = 0
f x ln 1 x x2
f x 0 x R2 x
2
1
f x 1 x 2
On the interval 0,.1 , 3 decreases, so
1 x
2 its maximum value occurs at the left end-point.
f x 1 x
2 2
K 3 3 2
3
1 0 1
f x 21 x
f 0 f 0 2
f x f 0 x x R2 x
1 2!
Remainder after 2nd order term

6. ex. 1: Find the Lagrange Error Bound for
where Tn(x) is the Taylor poly for ln 1 x at a = 0
Remainder Estimation Theorem
K x an 1
Tn ( x) f ( x) Rn x
n 1!
2
On the interval 0,.1 , 3 decreases, so
1 x
its maximum value occurs at the left end-point.
2 2
2.1 3 K 3 3 2
Rn x 1 0 1
3!
x2
x ln 1 x x error
Rn x 0.000333 2 Error is
.1 .0953102 .095 .000310 less than
Lagrange Error Bound error
bound.

7. Example: What is the maximum error in estimating cos
2.4 using the first 4 terms of the MacLaurin series
expansion of cosx?

8. Example: Find the value of n that would be needed to
estimate cos 2.4 to within 0.0000001 using the
MacLaurin series for f(x) = cosx?

9. Look at p. 510: #33, 36
Homerwork – p. 510: #29,30, 32,36, 38,39