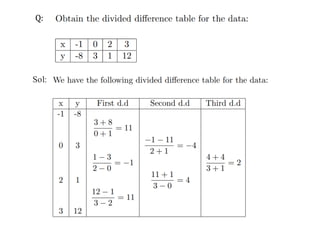
The document discusses interpolation and divided differences. It defines interpolation as finding the value of a dependent variable y for an independent variable x within the range of known x-values. Extrapolation is finding the value of y for an x outside this range. Lagrange interpolation uses a polynomial to find values that match the known (x,y) points. The error of interpolation is defined. Divided differences are introduced as a way to define polynomials used in Newton's interpolation formula. The relations between divided differences and forward differences are also covered.

2. Finding the value of y for an x between different
x - values x0,x1,...,xn is called problem of
Interpolation.
Finding the value of y for an x which falls outside
the range of x (x < x0 or x > xn) is called the
problem of Extrapolation.
MANIKANTA SATYALA

3. MANIKANTA SATYALA

4. MANIKANTA SATYALA
Let y = f(x) be continuous and differentiable in the
interval (a, b).
Given the set of (n + 1 ) values (x0, y0),(x1, y1), . . .
,(xn, yn) of x and y, where the values of x need not
necessarily be equally spaced.
It is required to find Pn(x), a polynomial of degree n
such that y and Pn(x) agree at the tabulated points.

5. MANIKANTA SATYALA
n
nnnn
n
n
n
n
n
y
xxxxxx
xxxxxx
y
xxxxxx
xxxxxx
y
xxxxxx
xxxxxx
))...()((
))...()((
...
))...()((
))...()((
))...()((
))...()((
110
110
1
12101
20
0
02010
21










 )()( xPnxfy
Here y is treated as dependent variable and expressed as
function of independent variable x

6. MANIKANTA SATYALA
n
nnnn
n
n
n
n
n
x
yyyyyy
yyyyyy
x
yyyyyy
yyyyyy
x
yyyyyy
yyyyyy
))...()((
))...()((
...
))...()((
))...()((
))...()((
))...()((
110
110
1
12101
20
0
02010
21









 )()( yPnygx
Here x is treated as dependent variable and expressed as
function of independent variable y

7. MANIKANTA SATYALA
Let x0, x1, x2, ....., xn be the ( n + 1 ) values of x which are not
necessarily equally spaced. Let y0, y1, y2, ....., yn be the ( n + 1 )
values of y = f( x ).
Let the polynomial of degree n for the function y = f( x ) passing
throughthe ( n + 1 ) points (x0, f (x0)), (x1, f (x1)), (x2, f (x2)),...,
(xn, f (xn)) be in the following form
y=f(x)= a0(x–x1)(x–x2) ... (x–xn)+a1(x–x0)(x–x2) ... (x–xn)+
a2(x–x0)(x–x1)(x–x3) ... (x–xn)+ --- +an(x–x0)(x–x1)…(x–xn-1)
....................... (1)
wherea0, a1, a2, ....., an are constants

8. MANIKANTA SATYALA
Since the polynomial passes through(x0, f(x0)),(x1, f(x1)),
(x2, f(x2)),...,(xn, f(xn)), the constants can be determined by
substituting one of the values of x0, x1, x2, ....., xn for x in the
above equation (1).
Putting x = x0 in (1) we get,
))...()(()( 0201000 nxxxxxxaxf 
))...()((
)(
02010
0
0
nxxxxxx
xf
a



9. MANIKANTA SATYALA
Putting x = x1 in (1) we get,
))...()(()( 1210111 nxxxxxxaxf 
))...()((
)(
12101
1
0
nxxxxxx
xf
a


Continuing in this manner and Putting x = xn in (1) we get,
))...()(()( 120  nnnnnn xxxxxxaxf
))...()((
)(
120 

nnnn
n
n
xxxxxx
xf
a

10. MANIKANTA SATYALA
Substituting these values of a0, a1, a2, ....., an in (1) , we get
n
nnnn
n
n
n
n
n
y
xxxxxx
xxxxxx
y
xxxxxx
xxxxxx
y
xxxxxx
xxxxxx
))...()((
))...()((
...
))...()((
))...()((
))...()((
))...()((
110
110
1
12101
20
0
02010
21










 )()( xPnxfy
This is known as Lagrange’s Interpolation Formula.

11. MANIKANTA SATYALA
Lagrange’s Interpolation Formula can be expressed


 


n
k
n
kj
j jk
j
k
xx
xx
xfxf
0 0 )(
)(
)()( 

12. MANIKANTA SATYALA
The values of x and y are given as below
x 5 6 9 11
F(x)=y 12 13 14 16
Find the values of y at x = 10
Here the values of x are not evenly spaced.
We have, x0=5, x1=6, x2=9, x3=11
And y0=12, y1=13, y2=14, y3=16
13
)116)(96)(56(
)1110)(910)(510(
12
)115)(95)(65(
)1110)(910)(610(
10 





y
67.1433.567.1133.42
16
)911)(611)(511(
)910)(610)(510(
14
)119)(69)(59(
)1110)(610)(510(









13. MANIKANTA SATYALA
Error in Interpolation: We assume that f(x) has continuous derivatives
of order unto (n+1) for all x ∈ (a, b). Since, f(x) is approximated by Pn(x),
the results contains errors. We define the error of interpolation or
truncation error as
Where
since, ξ is an unknown, it is difficult to find the value of error. However, we can find
a bound of the error. The bound of the error is obtained as
)(
)!1(
))...()((
)()(),( )1(10



 nn
n f
n
xxxxxx
xPxfxfE
),,...,,min(),,...,,min( 1010 xxxxxxxx nn  
)(max
)!1(
))...()((
),( )1(10





 n
ba
n
f
n
xxxxxx
xfE

14. MANIKANTA SATYALA
)(),...,(),( 10 nxfxfxfLet be the values of corresponding
To the arguments where the intervals
are not necessarily even spaced
f
nxxx ,...,, 10
11201 ,...,,  nn xxxxxx
Thenthe first divided difference of for the arguments
are defined by,nxxx ,...,, 10
f
12
12
21
01
01
10
)()(
),(
)()(
),(
xx
xfxf
xxf
xx
xfxf
xxf







15. MANIKANTA SATYALA
Thenthe Second divided difference of for the arguments
are defined by,nxxx ,...,, 10
f
02
1021
210
),(),(
),,(
xx
xxfxxf
xxxf



Thenthe nth divideddifference of for the arguments
are defined by,nxxx ,...,, 10
f
0
11021
10
),...,,(),...,,(
),...,,(
xx
xxxfxxxf
xxxf
n
nn
n


 
Note:-
The value of any divided difference is independent of the
order of the arguments.

16. MANIKANTA SATYALA
),,...,,(),...,,(
),,(),,(
),(),(
01110
012210
0110
xxxxfxxxf
xxxfxxxf
xxfxxf
nnn 


The divided differences are symmetrical with respect
to their arguments
The divided difference operator is linear.
The nth order divided differences of a polynomial of
degree n are constant, equal to the coefficient of xn

18. Q:
Sol:

19. ...),,())((),()()()( 2110100  xxxfxxxxxxfxxxfxf oo
),...,,,())...()()(( 211210 non xxxxfxxxxxxxx 
MANIKANTA SATYALA
An interpolation formula which has the property that a
polynomial of higher degree may be derived from it by simply
adding new terms
Let be the values of corresponding
To the arguments where the intervals
are not necessarily even spaced
The Newton’s divided difference interpolation formula is
nxxx ,...,, 10
11201 ,...,,  nn xxxxxx
f)(),...,(),( 10 nxfxfxf

20. MANIKANTA SATYALA
 1),()()()( 000  xxfxxxfxf
Let be the values of corresponding
To the arguments where the intervals
are not necessarily even spaced
nxxx ,...,, 10
11201 ,...,,  nn xxxxxx
f)(),...,(),( 10 nxfxfxf
0
0
0
)()(
),(
xx
xfxf
xxf


By the first order divided difference
Further by 2nd order difference
1
100
10
),(),(
),,(
xx
xxfxxf
xxxf



 2),,()(),(),( 101100  xxxfxxxxfxxf

21. MANIKANTA SATYALA
),,())((),()()()( 10101000 xxxfxxxxxxfxxxfxf 
Substituting (2) in (1) we get
Similarly by 3rd order difference and above equation we have
By proceeding in the same way, get
),,())((),()()()( 210101000 xxxfxxxxxxfxxxfxf 
),,,())()(( 210210 xxxxfxxxxxx 
),,())((),()()()( 210101000 xxxfxxxxxxfxxxfxf 
...),,,())()(( 3210210  xxxxfxxxxxx
),..,,,())...()()((... 2101210 nn xxxxfxxxxxxxx 
),..,,,())...()()((... 1210210  nn xxxxfxxxxxxxx

22. MANIKANTA SATYALA
Since the function is a polynomial of degree n, therefore
Hence we get
This is know as Newton’s Divided Difference formula.
),,())((),()()()( 210101000 xxxfxxxxxxfxxxfxf 
...),,,())()(( 3210210  xxxxfxxxxxx
),..,,,())...()()((... 2101210 nn xxxxfxxxxxxxx 
)(xf
0),..,,,( 1210  nxxxxf

23. Note :- Relation between forward and divided differences exits at equal intervals
1st order :-
h
y
h
yy
xxfxxf
h
y
h
yy
xx
xfxf
xxf
h
y
h
yy
xx
xfxf
xxf
kkk
kkkk
11
11
112
12
12
21
001
01
01
10
),(),(
)()(
),(
)()(
),(




















2nd order :- 2
0
2
01
02
1021
210
22
),(),(
),,(
h
y
h
h
y
h
y
xx
xxfxxf
xxxf









3rd order :- 3
0
3
3
0
32
0
2
2
1
2
02
210321
3210
!363
22),,(),,(
),,,(
h
y
h
y
h
h
y
h
y
xx
xxxfxxxf
xxxxf











MANIKANTA SATYALA

24. h
y
xxfxxf k
kkkk

  ),(),( 111st order :-
2nd order :-
3rd order :-
2
2
21
!2
),,(
h
y
xxxf k
kkk


...
...
...
!3
),,,( 3
3
321
h
y
xxxxf k
kkkk


kth order :- k
k
kkk
hk
y
xxxxfxxxf
!
),,...,,(),...,,( 0
01110

 
MANIKANTA SATYALA

25. MANIKANTA SATYALA
Note :- Relation between backward and divided differences exits at equal intervals
1st order :-
h
y
h
yy
xxfxxf
h
y
h
yy
xx
xfxf
xxf
h
y
h
yy
xx
xfxf
xxf
kkk
kkkk




















1
11
212
12
12
21
101
01
01
10
),(),(
)()(
),(
)()(
),(
2nd order :-
2
2
2
12
02
1021
210
22
),(),(
),,(
h
y
h
h
y
h
y
xx
xxfxxf
xxxf









3rd order :-
3
3
3
3
3
32
2
2
2
3
2
02
210321
3210
!363
22),,(),,(
),,,(
h
y
h
y
h
h
y
h
y
xx
xxxfxxxf
xxxxf












26. MANIKANTA SATYALA
h
y
xxfxxf k
kkkk

  ),(),( 111st order :-
2nd order :-
3rd order :-
2
2
2
21
!2
),,(
h
y
xxxf k
kkk




...
...
...
!3
),,,( 3
3
3
321
h
y
xxxxf k
kkkk




kth order :- k
k
k
kkk
hk
y
xxxxfxxxf
!
),,...,,(),...,,( 01110

 