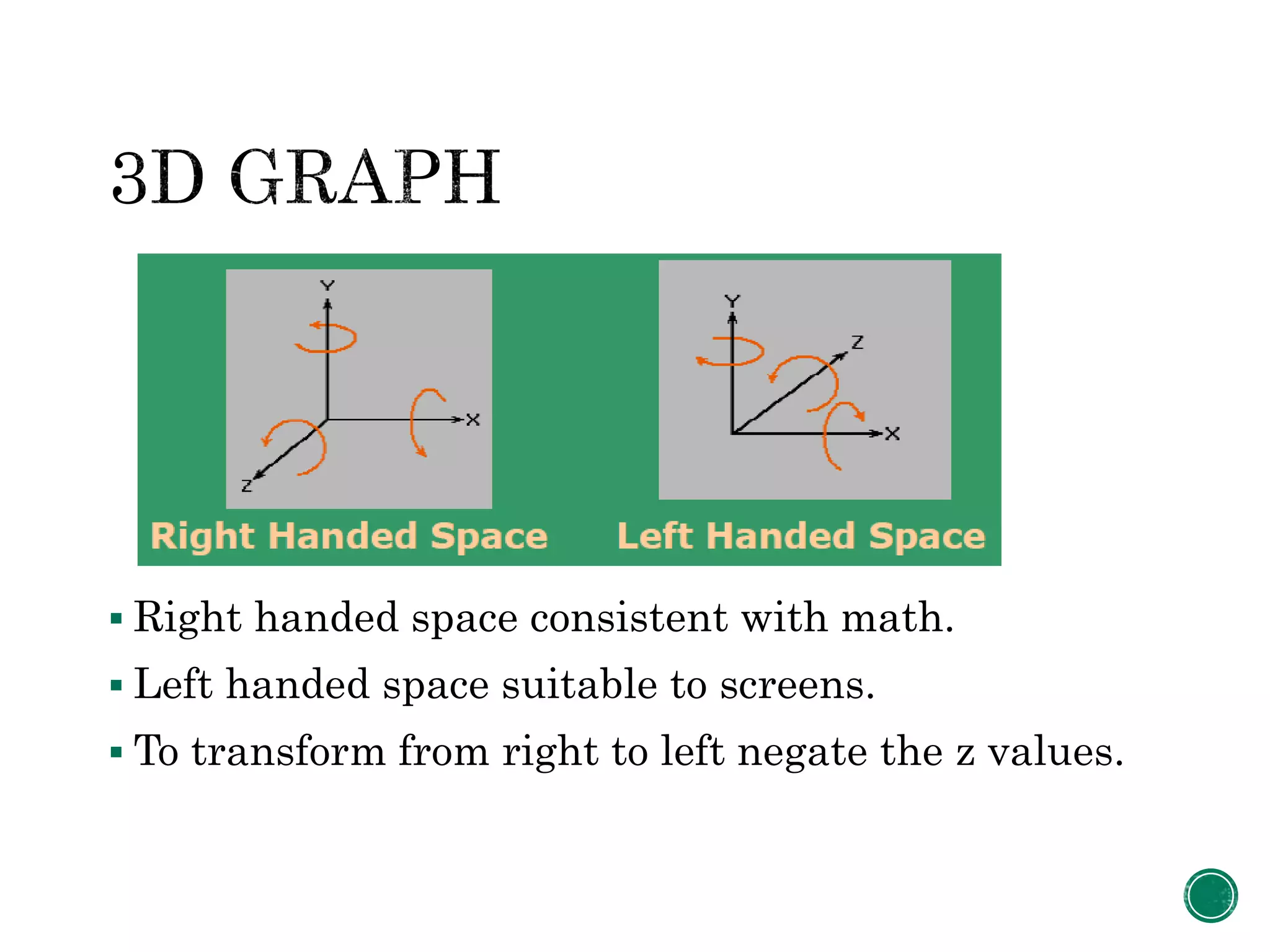
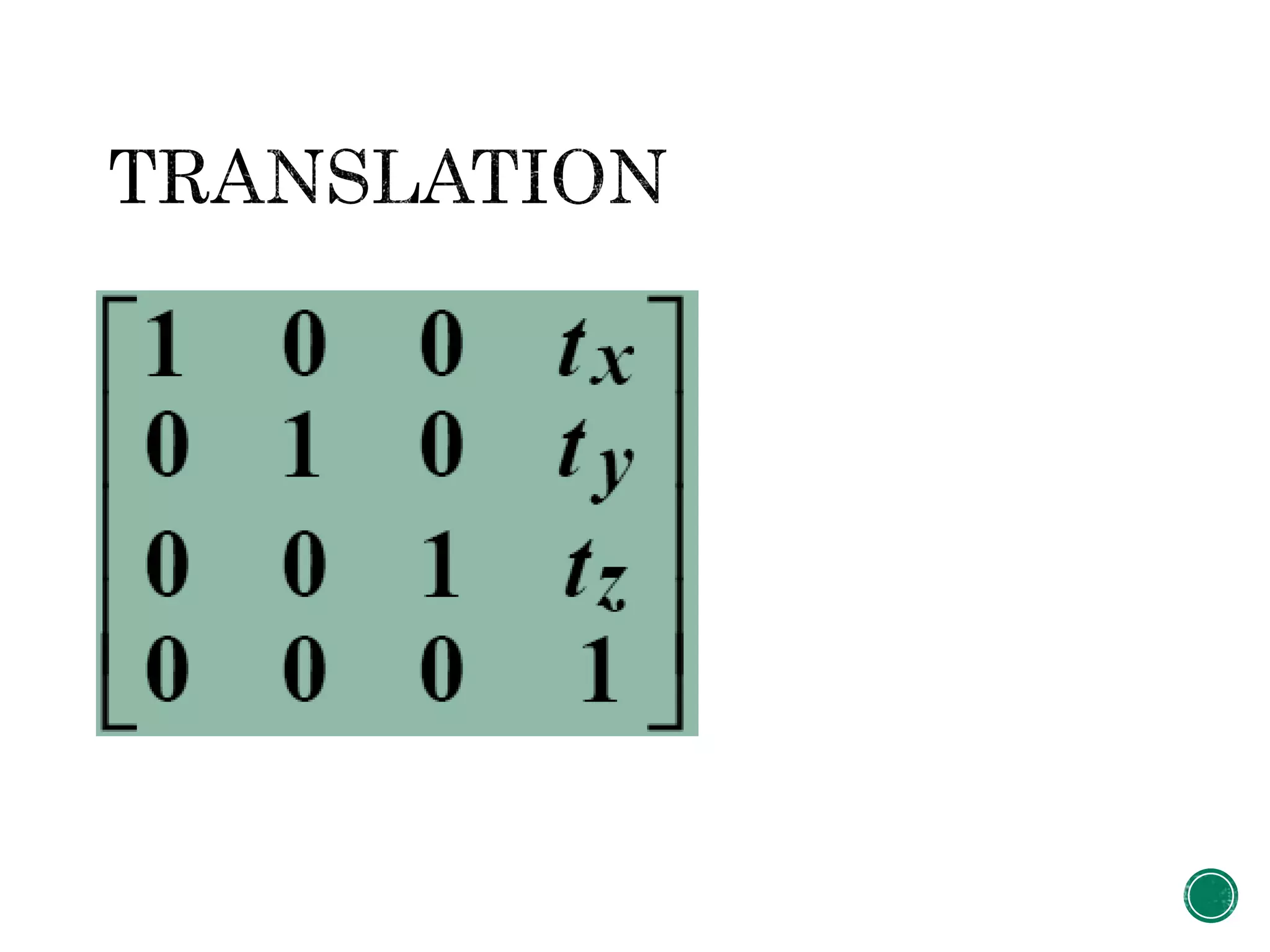
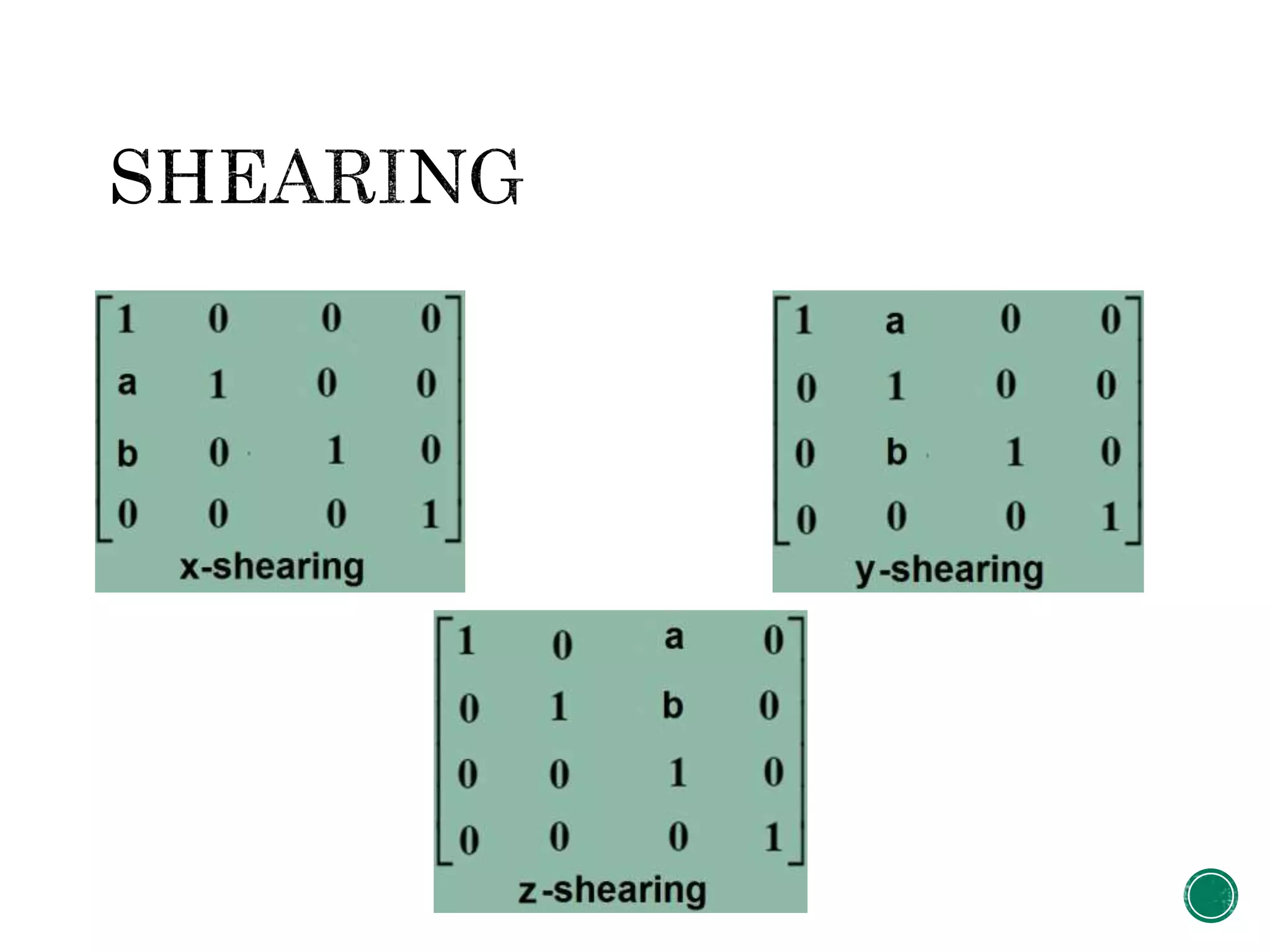
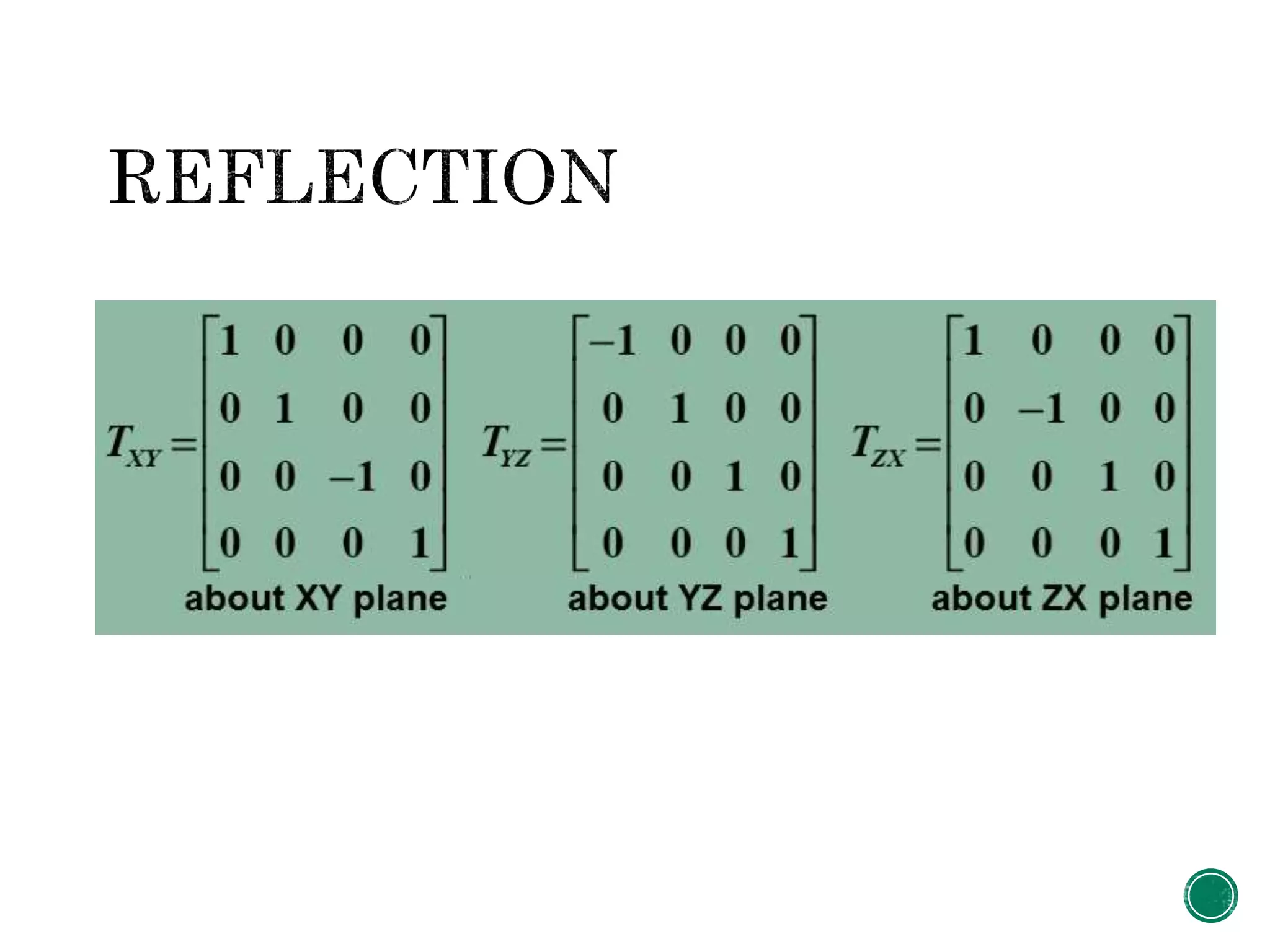
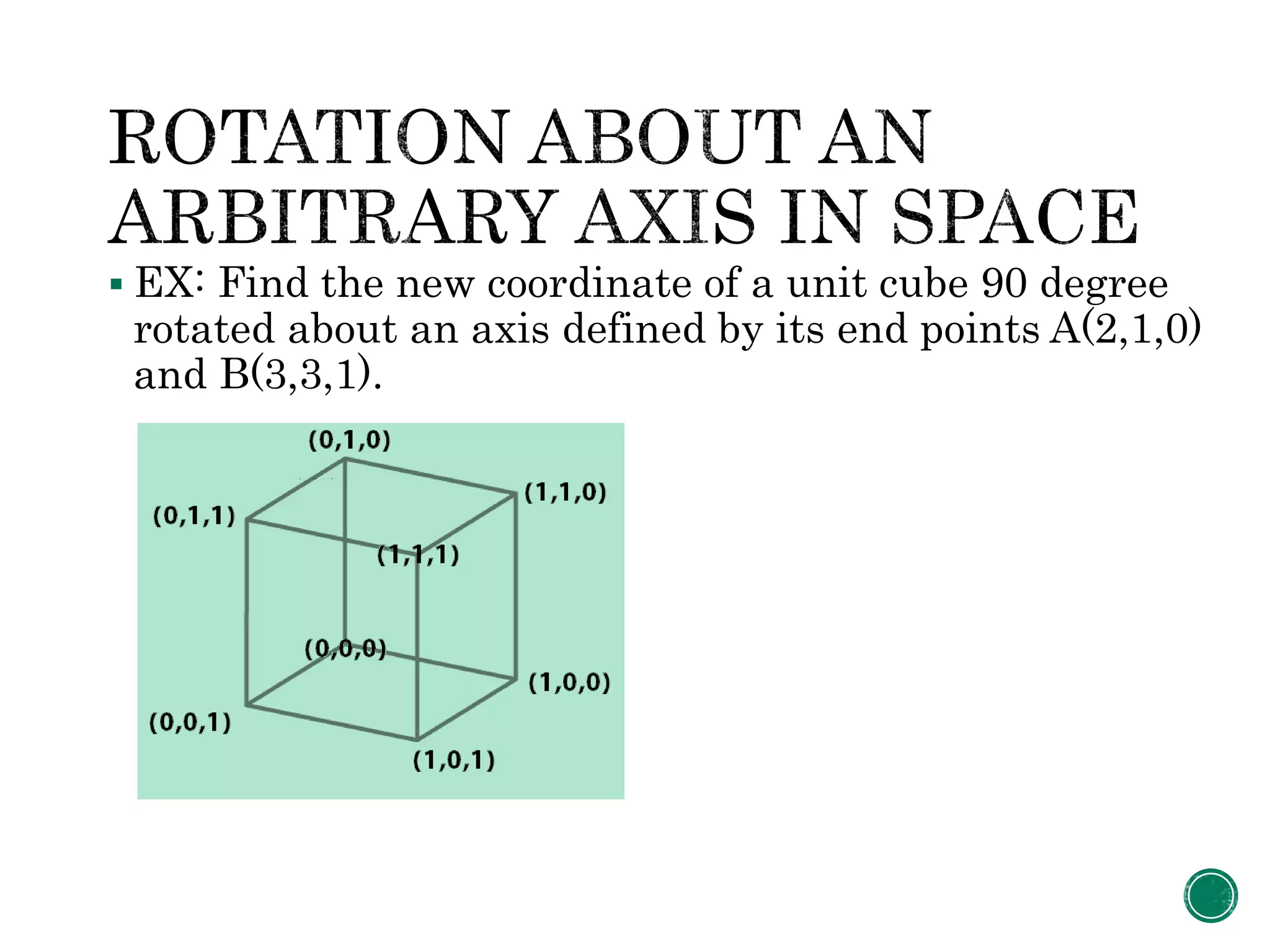
1. The document describes the steps to perform a rotation of an object in 3D space about an arbitrary point or axis. 2. It provides an example of rotating a unit cube 90 degrees about an axis defined by two points and calculating the new coordinates. 3. It also gives an example of rotating the point (1,2,1) 90 degrees and showing the resulting point (1,2,3) transformed to (4,6,7).

2.  Right handed space consistent with math.
 Left handed space suitable to screens.
 To transform from right to left negate the z values.

8.  There are five steps for reflection about an arbitrary
point in space:
1. Translate to the origin by –(x0,y0,z0).
2. Rotate (x’,y’,z’) about x-axis.
3. Rotate (x’,y’,z’) about y-axis.
4. Rotate about z-axis.
5. Inverse step 2 By changing the sin sign.
6. Inverse step 3 By changing the sin sign.
7. Inverse step 1 By changing the tx, ty and tz sign.

9.  EX: Find the new coordinate of a unit cube 90 degree
rotated about an axis defined by its end points A(2,1,0)
and B(3,3,1).

10.  Step 1: Translate to origin
 a= 3-2= 1
 b= 3-1= 2
 c= 1-0= 1
1 0 0 -2
0 1 0 -1
0 0 1 0
0 0 0 1

11.  Step 2: Rotation about x-axis
 D= 𝑏2 + 𝑐2 = 22 + 12 = 5
 Sin= b/d= 2/ 5
 Cos= c/d= 1/ 5
1 0 0
0
0 1/ 5 -2/ 5
1
0 2/ 5 1/ 5
1
0 0 0
1

12.  Step 3: Rotation about y-axis
 L= 𝑎2 + 𝑏2 + 𝑐2 = 6
 Sin= a/L= 1/ 6
 Cos= d/L= 5/ 6
5/ 6 0 -1/ 6 0
0 1 0 0
1/ 6 0 5/ 6 0
0 0 0 1

13.  Step 4: Rotation about z-axis by 90 degree
0 -1 0 0
1 0 0 0
0 0 1 0
0 0 0 1

14.  Step 5: Inverse Rotation about x-axis
1 0 0
0
0 1/ 5 2/ 5
1
0 -2/ 5 1/ 5
1
0 0 0
1

15.  Step 6: Inverse Rotation about y-axis
5/ 6 0 1/ 6 0
0 1 0 0
−1/ 6 0 5/ 6 0
0 0 0 1

16.  Step 7: Inverse of Translation
 Then we multiply all the matrices with each other.
1 0 0 2
0 1 0 1
0 0 1 0
0 0 0 1

17.  EX: Find the rotation for the point (1,2,1) by 90 degree
(1,2,3)
(4,6,7)

18.  Step 1: Translate to origin
 A= 4-1= 3
 B= 6-2= 4
 C= 7-3= 4
1 0 0 -1
0 1 0 -2
0 0 1 -3
0 0 0 1

19.  Step 2: Rotation about x-axis
 D= 𝑏2 + 𝑐2 = 42 + 42 = 32
 Sin= b/d= 4/ 32
 Cos= c/d= 4/ 321 0 0
0
0 4/ 32 -4/ 32 1
0 4/ 32 4/ 32
1
0 0 0
1

20.  Step 3: Rotation about y-axis
 L= 𝑎2 + 𝑏2 + 𝑐2 = 41
 Sin= a/L= 3/ 41
 Cos= d/L= 32/ 6
32/ 41 0 -3/41 0
0 1 0 0
3/ 41 0 32/ 41 0
0 0 0 1

21.  Step 4: Rotation about z-axis by 90 degree
0 -1 0 0
1 0 0 0
0 0 1 0
0 0 0 1

22.  Step 5: Inverse step 2
1 0 0
0
0 4/ 32 4/ 32 1
0 -4/ 32 4/ 32 1
0 0 0
1

23.  Step 6: Inverse step 3
32/ 41 0 3/ 41 0
0 1 0 0
-3/ 41 0 32/ 41 0
0 0 0 1

24.  Step 1: Inverse step 1
 Then we multiply all the matrices with each other and
with the point (1,2,1).
1 0 0 1
0 1 0 2
0 0 1 3
0 0 0 1