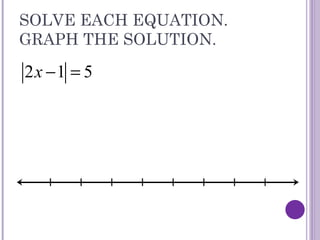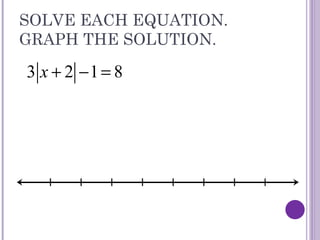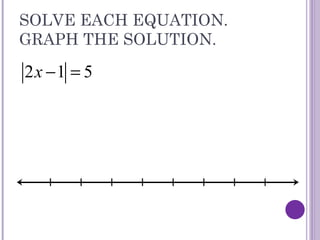
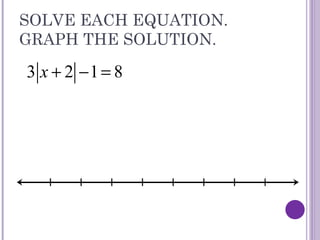
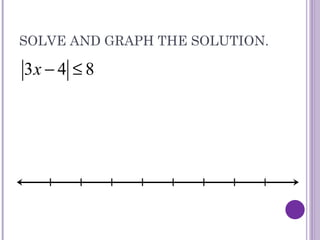
This document discusses absolute value equations and inequalities. It explains that absolute value equations can have two solutions because opposites have the same absolute value. It provides steps for solving absolute value equations which include isolating the absolute value and removing the absolute value signs. Solutions then need to be checked for extraneous solutions, which are solutions that do not satisfy the original equation. The document also covers absolute value inequalities and how to write them as compound inequalities without absolute value symbols in order to solve and graph the solutions.

1. 1.6 ABSOLUTE VALUE EQUATIONS AND INEQUALITIES

2. ABSOLUTE VALUE The absolute value of a real number x , written | x |, is its distance from zero on the number line Example: |5| = 5 |-5| = 5

3. ABSOLUTE VALUES EQUATION An absolute value equation is an equation that has a variable inside the absolute value sign Absolute value equations can have two answers because opposites have the same absolute value.

4. SOLVING ABSOLUTE VALUE EQUATIONS To solve an absolute value equation: Isolate the absolute value remove the absolute value signs and set up as shown:

5. SOLVE EACH EQUATION. GRAPH THE SOLUTION.

6. SOLVE EACH EQUATION. GRAPH THE SOLUTION.

7. SOLVE EACH EQUATION. GRAPH THE SOLUTION.

8. SOLVE EACH EQUATION. GRAPH THE SOLUTION.

9. EXTRANEOUS SOLUTIONS An extraneous solution is a solution derived from an original equation that is not a solution of the original equation. Remember that the absolute value measures the distance from zero on a number line. Distance can never be negative. Therefore, we must check our answers when working with absolute values.

10. SOLVE AND CHECK FOR EXTRANEOUS SOLUTIONS.

11. SOLVE AND CHECK FOR EXTRANEOUS SOLUTIONS.

12. SOLVE AND CHECK FOR EXTRANEOUS SOLUTIONS.

13. ABSOLUTE VALUE INEQUALITIES An absolute value inequality is an inequality that has a variable inside the absolute value sign.

14. SOLVING ABSOLUTE VALUE INEQUALITIES Write the absolute value inequality as a compound inequality without absolute value symbols

16. SOLVE AND GRAPH THE SOLUTION.

17. SOLVE AND GRAPH THE SOLUTION.

18. SOLVE AND GRAPH THE SOLUTION.