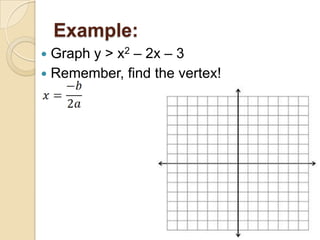
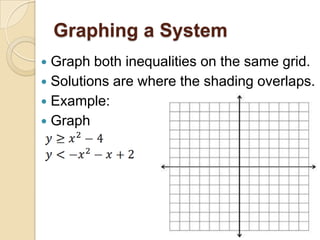
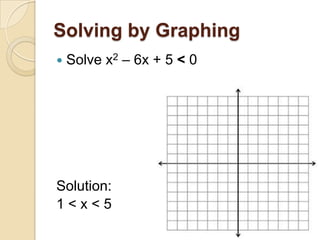
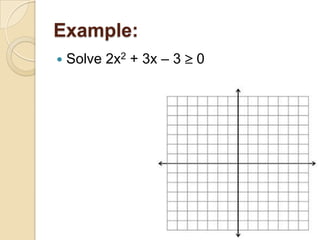
This document discusses how to graph and solve quadratic inequalities in one and two variables. It provides examples of graphing quadratic inequalities by drawing the parabola, choosing a test point, and shading the appropriate region. Systems of quadratic inequalities can be graphed on the same grid, with the shared shaded region representing the solutions. Quadratic inequalities in one variable can also be solved by graphing the parabola and identifying the x-values where it lies above or below the x-axis, or algebraically by solving the inequality as an equation and testing values between the solutions.

1. 5.7 Graphing and Solving
Quadratic Inequalities

2. Quadratic Inequalities in Two
Variables
 Four types:
 To graph:
1. Draw the parabola.
>,< : dashed line , : solid line
2. Choose a point from the inside and
plug it in
3. If true, shade inside. If false, shade
outside.

3. Example:
 Graph y > x2 – 2x – 3
 Remember, find the vertex!

4. Your Turn!
 Graph y 2x2 - 5x – 3

5. Graphing a System
 Graph both inequalities on the same grid.
 Solutions are where the shading overlaps.
 Example:
 Graph

6. Quadratic Inequalities in One
Variable
 Can be solved using a graph.
 To solve ax2 + bx + c < 0 (or 0), graph the
parabola and identify on which x-values the
graph lies below the x-axis.
 To solve ax2 + bx + c > 0 (or 0), identify
on which x-values the graph lies above the
x-axis.
 Find the intercepts by solving for x.
(Remember: solutions = zeros = x-intercepts)

7. Solving by Graphing
 Solve x2 – 6x + 5 < 0
Solution:
1<x<5

8. Example:
 Solve 2x2 + 3x – 3 0

9. Your Turn!
 Solve -x2 – 9x + 36 > 0

10. Solving Algebraically
1. Write as an equation and solve.
2. Plot the solutions (called critical x-values)
on a number line.
3. Test an x-value in between the critical
values.
If it is true, solution is an “and”
If it is not true, solution is an “or”

11. Example:
 Solve x2 + 2x 8

12. Your Turn!
 Solve 2x2 – x > 3