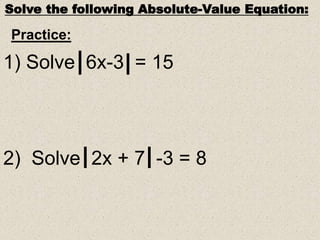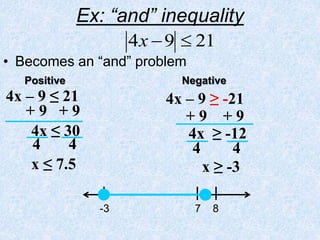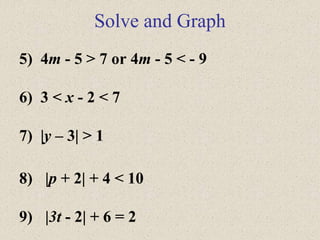This document provides information and examples for solving absolute value equations and inequalities. It begins with definitions of absolute value and discusses how absolute value equations can have two solutions since the expression inside the absolute value can be positive or negative. Examples are provided for solving absolute value equations by setting the expression equal to both its positive and negative values. The document also discusses how to solve absolute value inequalities by splitting them into "and" or "or" statements and provides examples of solving and graphing various absolute value inequalities.

1. Warm-Up:
Describe the similarities and differences between
equations and inequalities.
Name:
Date:
Period:
Topic: Solving Absolute Value Equations & Inequalities
Essential Question: What is the process needed to solve
absolute value equations and inequalities?

2. Home-Learning #2 Review

3. Quiz #7:

4. Recall :
Absolute value | x | : is the distance
between x and 0. If | x | = 8, then
– 8 and 8 is a solution of the
equation ; or | x |  8, then any
number between 8 and 8 is a
solution of the inequality.

5. Absolute Value (of x)
• Symbol lxl
• The distance x is from 0 on the number line.
• Always positive
• Ex: l-3l=3
-4 -3 -2 -1 0 1 2
You can solve some absolute-value
equations using mental math. For
instance, you learned that the equation
| x | 3 has two solutions: 3 and 3.
To solve absolute-value equations, you
can use the fact that the expression inside
the absolute value symbols can be either
positive or negative.
Recall:

6. Solving an Absolute-Value Equation:
Solve | x  2 |  5 Solve | 2x  7 |  5  4

7. Solving an Absolute-Value Equation
| 7  2 |  | 5 |  5 | 3  2 |  | 5 |  5
Solve | x  2 |  5
The expression x  2 can be equal to 5 or 5.
x  2 IS POSITIVE
| x  2 |  5
x  2  5
x  7 x  3
x  2 IS NEGATIVE
| x  2 |  5
x  2  5
The equation has two solutions: 7 and –3.
CHECK
Answer ::

8. Solve | 2x  7 |  5  4
2x  7 IS POSITIVE
| 2x  7 |  5  4
| 2x  7 |  9
2x  7  +9
2x  16
2x  7 IS NEGATIVE
| 2x  7 |  5  4
| 2x  7 |  9
2x  7  9
2x  2
x  1
Isolate the absolute value expression on one side of the equation.
Isolate the absolute value expression on one side of the equation.
SOLUTION
2x  7 IS POSITIVE
2x  7  +9
2x  7 IS NEGATIVE
2x  7  9
2x  7 IS POSITIVE
| 2x  7 |  5  4
| 2x  7 |  9
2x  7  +9
2x  16
2x  7 IS NEGATIVE
| 2x  7 |  5  4
| 2x  7 |  9
2x  7  9
2x  2
TWO SOLUTIONS
x  8
x  1
Answer ::

9. Solve the following Absolute-Value Equation:
Practice:
1) Solve 6x-3 = 15
2) Solve 2x + 7 -3 = 8

10. 1) Solve 6x-3 = 15
6x-3 = 15 or 6x-3 = -15
6x = 18 or 6x = -12
x = 3 or x = -2
* Plug in answers to check your solutions!
Answer ::

11. 2) Solve 2x + 7 -3 = 8
Get the abs. value part by itself first!
2x+7 = 11
Now split into 2 parts.
2x+7 = 11 or 2x+7 = -11
2x = 4 or 2x = -18
x = 2 or x = -9
Check the solutions.
Answer ::

12. ***Important NOTE***
3 2x + 9 +12 = 10
- 12 - 12
3 2x + 9 = - 2
3 3
2x + 9 = - 2
3
What about this absolute value equation? 3x – 6 – 5 = – 7

14. Solving an Absolute Value Inequality:
● Step 1: Rewrite the inequality as a conjunction or a
disjunction.
● If you have a you are working with a
conjunction or an ‘and’ statement.
Remember: “Less thand”
● If you have a you are working with a
disjunction or an ‘or’ statement.
Remember: “Greator”
● Step 2: In the second equation you must negate the
right hand side and reverse the direction of the
inequality sign.
● Solve as a compound inequality.
or
 
or
 

15. Ex: “and” inequality
• Becomes an “and” problem
21
9
4 

x
-3 7 8
4x – 9 ≤ 21
+ 9 + 9
4x ≤ 30
x ≤ 7.5
4 4
4x – 9 ≥ -21
+ 9 + 9
4x ≥ -12
x ≥ -3
4 4
Positive Negative

16. |2x + 1| > 7
This is an ‘or’
statement.
(Greator).
3
-4
Ex: “or” inequality
2x + 1 > 7 or 2x + 1 < - 7
– 1 - 1 – 1 - 1
2x > 6 2x < - 8
2 2 2 2
x > 3
In the 2nd
inequality, reverse
the inequality sign
and negate the
right side value.

17. Solve | x  4 | < 3 and graph the solution.
Solving Absolute Value Inequalities:
Solve | 2x  1 | 3  6 and graph the solution.

18. Solve | x  4 | < 3
x  4 IS POSITIVE x  4 IS NEGATIVE
| x  4 |  3
x  4  3
x  7
| x  4 |  3
x  4  3
x  1
Reverse
inequality symbol.

This can be written as 1  x  7.
The solution is all real numbers greater than 1 and less than 7.
Answer ::

19. Solve | 2x  1 | 3  6 and graph the solution.
| 2x  1 |  3  6
| 2x  1 |  9
2x  1  +9
x  4
2x  8
| 2x  1 | 3  6
| 2x  1 |  9
2x  1  9
2x  10
x  5
2x + 1 IS POSITIVE 2x + 1 IS NEGATIVE
 6  5  4  3  2  1 0 1 2 3 4 5 6
The solution is all real numbers greater than or equal
to 4 or less than or equal to  5. This can be written as the
compound inequality x   5 or x  4.
Reverse
inequality
symbol.
Answer ::

20. 11
3
2
3 


x
3)
Solve and graph the following
Absolute-Value Inequalities:
4) |x -5| < 3

21. Solve & graph.
• Get absolute value by itself first.
• Becomes an “or” problem
11
3
2
3 


x
8
2
3 

x
8
2
3
or
8
2
3 



 x
x
6
3
or
10
3 

 x
x
2
or
3
10


 x
x
-2 3 4
Answer ::
3)

22. 4) |x -5|< 3
x -5< 3 and x -5< 3
x -5< 3 and x -5> -3
x < 8 and x > 2
2 < x < 8
This is an ‘and’ statement.
(Less thand).
Rewrite.
In the 2nd inequality, reverse the
inequality sign and negate the
right side value.
Solve each inequality.
Graph the solution.
8
2
Answer ::

23. Solve and Graph
5) 4m - 5 > 7 or 4m - 5 < - 9
6) 3 < x - 2 < 7
7) |y – 3| > 1
8) |p + 2| + 4 < 10
9) |3t - 2| + 6 = 2

24. Home-Learning #3:
• Page 211 - 212 (18, 26,36, 40, 64)