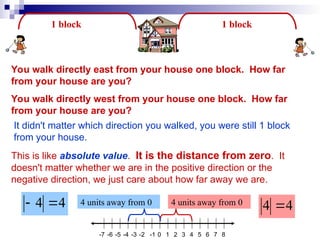
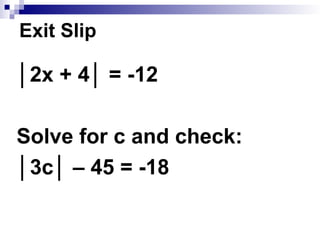The document outlines a lesson plan focused on solving absolute value equations, including definitions and problem-solving techniques. It provides a structured agenda with specific tasks and examples, highlighting the importance of isolating absolute values and checking solutions. Additionally, it emphasizes real-life applications of absolute value and establishes a timeline for upcoming tests and assignments.

1. Tues, 3/5
SWBAT… solve absolute value equations
Agenda
1. WU (5 min)
2. Binder check (10 min)
3. 5 Examples: absolute value equations (25 min)
Warm-Up:
1. Place your test corrections and get ready for the next unit on your desk.
2. Take out your binder.
3. Set-up notes. Topic = “Solving Absolute Value Equations.”
HW#1: Absolute value equations

2. New unit on Absolute Value & Inequalities
(3 weeks) Daily HW, WU, exit slips, weekly quizzes
SWBAT…
1. Solve absolute value equations.
2. Solve and graph one-step inequalities involving addition,
subtraction, multiplication, and division.
3. Solve and graph multi-step inequalities.
4. Write inequalities in interval notation.
5. Solve and graph compound inequalities.
6. Graph inequalities with two variables.
7. Graph system of inequalities.
Unit test on Friday, March 22 (before Spring Break)

3. Solving Absolute Value Equations

4. You walk directly east from your house one block. How far
from your house are you?
1 block
1 block
You walk directly west from your house one block. How far
from your house are you?
It didn't matter which direction you walked, you were still 1 block
from your house.
This is like absolute value. It is the distance from zero. It
doesn't matter whether we are in the positive direction or the
negative direction, we just care about how far away we are.
2
-7 -6 -5 -4 -3 -2 -1 1 5 7
3
0 4 6 8
4
4 
4 units away from 0
4
4 
 4 units away from 0

5. Using Absolute Value in Real Life
Using Absolute Value in Real Life
The graph shows the position of
a diver relative to sea level. Use
absolute value to find the diver’s
distance from the surface.

6. Definition of Absolute Value
 The distance from any number to zero on
the number line.
 The value is always positive. Why?
Because absolute value is a distance and
distance is always positive.

7. Ex. #1
|x| = 6
x = 6 or x = -6
Check:
|x | = 6 or |x| = 6
| 6 | = 6 | -6 | = 6
6 = 6 6 = 6
To solve an absolute value equation:
1. Isolate the absolute value on one side of the equal
sign.
2. Case 1: Set the inside of the absolute value equal to
a positive of the other given expression. Solve.
3. Case 2 : Set the inside the absolute value equal to
the negative of the other given expression. Solve.
4. Check both solutions.

8. 6

x
What we are after here are values of x such
that they are 6 away from 0.
2
-7 -6 -5 -4 -3 -2 -1 1 5 7
3
0 4 6 8
6 and -6 are both 6 units away from 0
6
or
6 

 x
x

9. Ex. #2
|x + 3| = 7
x + 3 = 7 or x + 3 = -7 Subtract 3 from both sides
x = 4 or x = -10
Check:
|x + 3| = 7 or |x + 3| = 7
| 4 + 3| = 7 | -10 + 3| = 7
|7| = 7 |-7| = 7
7 = 7 7 = 7
To solve an absolute value equation:
1. Isolate the absolute value on one side of the equal
sign.
2. Case 1: Set the inside of the absolute value equal to
a positive of the other given expression. Solve.
3. Case 2 : Set the inside the absolute value equal to
the negative of the other given expression. Solve.
4. Check both solutions.

10. Ex. #3
|15 – 3x| = 6
15 – 3x = 6 or 15 – 3x = -6 .
-3x = -9 -3x = -21 Subtract 15 from both sides.
x = 3 or x = 7 Divide both sides by –3.
Check:
|15 – 3x| = 6 |15 – 3x| = 6
|15 – 3(3)| = 6 |15 – 3(7)| = 6
|6| = 6 |–6| = 6
6 = 6 6 = 6

11. Ex. #4
| x | – 6 = -3
| x | = 3 Add 6 to both sides
x = 3 or x = -3
Check:
|x | - 6 = -3 or |x| - 6 = -3
| 3 | = 3 | -3 | = 3
3 = 3 3 = 3

12. Ex. #5
│-3c│ – 10 = -4
│-3c│ = 6 Add 10 to both sides
-3c = 6 or -3c = -6 Divide both sides by -3
c = -2 or c = 2

13. Ex. #6
2| x | = -10
| x | = -5
No Solution

14. Absolute Value and No Solutions
 Absolute value is always positive (or zero). An
equation such as │x │= -5 or │x – 4│= -6 is
never true.
 It has NO Solution.
 │x │= -5 has no solution
And this is negative
This is a distance
Ever heard of a negative distance?

15. OYO (On Your Own)
Solve:
1.) │2x + 4│ = 12
2.) 3│x│= 6
3.) │2x + 4│ – 12 = -12

16. │2x + 4│ = -12
Solve for c and check:
│3c│ – 45 = -18
Exit Slip