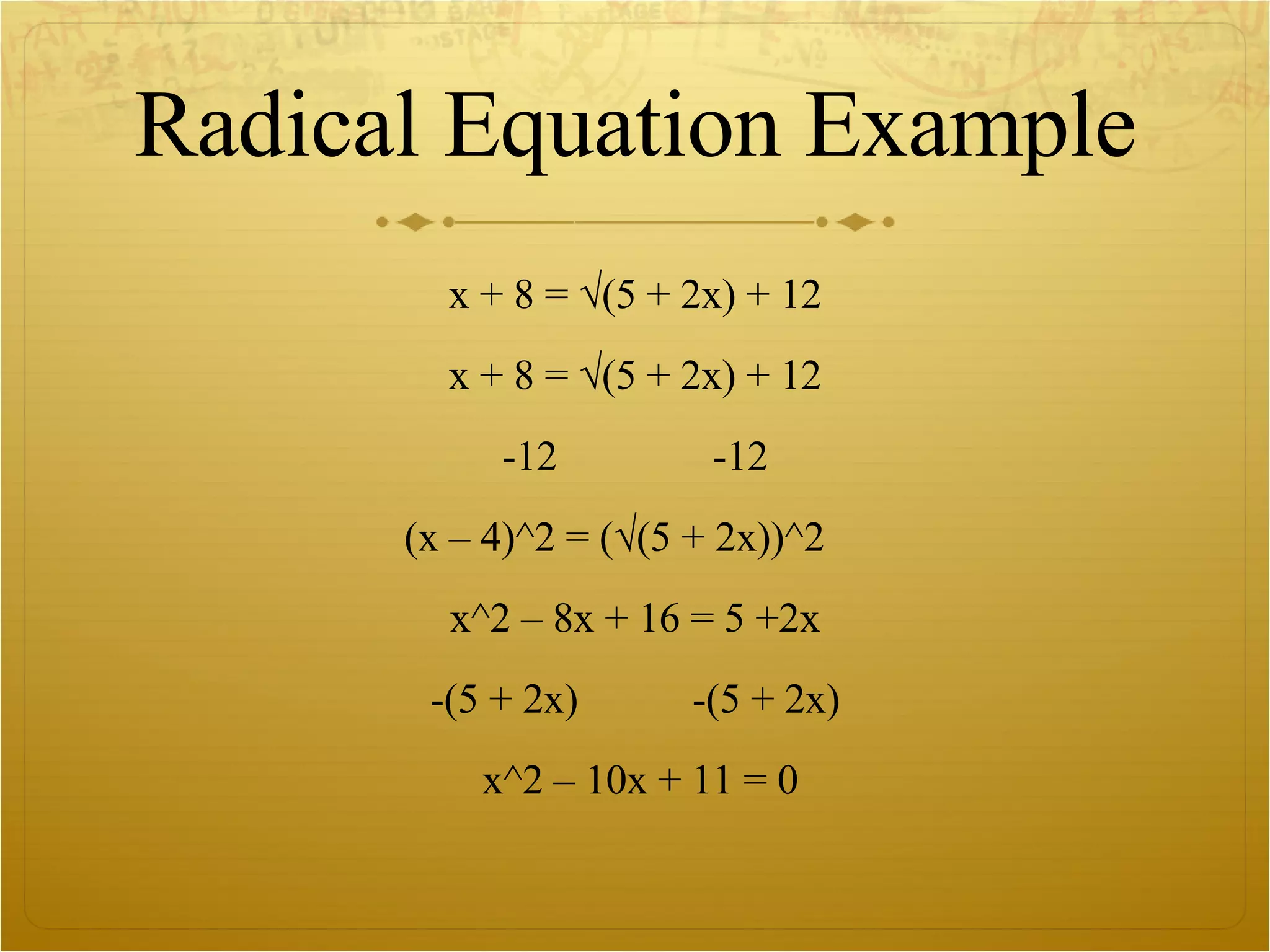This document provides an overview of solving different types of equations and inequalities, including linear equations, quadratic equations, rational equations, radical equations, linear inequalities, quadratic inequalities, and graphing methods. Key methods discussed are factoring, the quadratic formula, completing the square, manipulating fractions to get a common denominator, squaring both sides of an equation to eliminate radicals, and determining shading regions for inequalities based on a test point.

1. Solving Equations and Inequalities Lindsay Lehman And Dana Bailey

2. Linear Equations 5x + 3 = 28 -3 -3 5x = 25 ÷ 5 ÷5 x = 5

3. Quadratic Equations There are multiple ways to solve quadratic equations. These include: Factoring The quadratic formula Completing the square

4. Factoring x^2 + 8x = -15 +15 +15 x^2 + 8x + 15 = 0 (x + 3)(x + 5) = 0 x + 3 = 0 x + 5 = 0 x = -3 and x = -5 Always plug your solutions back into the original equation to check for extraneous solutions.

5. Using the Quadratic Formula The quadratic formula is: (-b) ± √(b^2)-4(a)(c) 2(a) When trying to solve quadratic equations and factoring doesn’t work, the alternative is to use the quadratic formula. It always works. Simply take the parts of the equation and plug them into the formula. Then solve.

6. Quadratic Formula Example x^2 + 4x – 7 = 0 This equation does not factor, or at least not easily. Simply identify a, b, and c and plug them in to the quadratic formula. For this equation: A = 1 B = 4 C = -7

7. Quadratic Example Continued X = (-4)± √4^2 – 4(1)(-7) 2(1) Now just solve (-4) + 2√11 = X (-4) – 2√11 = X 2 2

8. Completing the Square Another alternative to use when a quadratic equation may not be factored easily is completing the square. When you have an equation: Ax^2 + Bx + C = 0 Just pull C to the opposite side (by subtracting or adding it). Then, to make Ax^2 + Bx a perfect square, just add (b/2)^2 to both sides of the equation. Once this is completed, write the equation in factored form, (x + b/2)^2 = c + (b/2)^2, then solve.

9. Completing the Square Example x^2 + 2x - 4 = 0 x^2 + 2x + __ = 4 x^2 + 2x + 1 = 4 + 1 (x + 1)^2 = 5 x + 1 = ± √5 x = -1 ± √5

10. Rational Equations Rational equations are basically fractions set equal to each other with variables in them. All you have to do is get a common denominator (so that you can cancel them out), then solve the two expressions set equal to each other. Or, if there is only a denominator on one side, you can multiply both sides by the common denominator to get rid of it, then solve.

11. Rational Equation Example 2x + 5 = 15 4 2x + 5 = (15x)4 2x + 5 = 60 2x = 55 x = 27.5

12. Radical Equations Radical Equations are equations that have radicals in them. They look tricky to deal with, but when you know how to handle them it’s not so bad.

13. How to Solve Radical Equations Solving radical is actually very simple. Just follow these steps: First, one must get the radical by itself on one side of the equation. Then, one must square both sides (in order to eliminate the square root). Once the square root is gone, simply solve the equation. Finally, NEVER forget to check all solutions to weed out any extraneous ones.

14. Radical Equation Example x + 8 = √(5 + 2x) + 12 x + 8 = √(5 + 2x) + 12 -12 -12 (x – 4)^2 = (√(5 + 2x))^2 x^2 – 8x + 16 = 5 +2x -(5 + 2x) -(5 + 2x) x^2 – 10x + 11 = 0

15. Radical Equation Ex. Continued x = -(-10) ± √( 100 – 4(1)(11)) 2(1) x = 10 ± √(56) 2 2 = 5 ± √(14) Solutions: x ≈ 8.74, x ≈ 1.26

16. Inequalities Inequalities are equations with symbols in place of where the equals sign would be in a regular equation. There are four different signs, they are: > - Greater than < - Less than ≤ - Less than or equal to ≥ - Greater than or equal to

17. Linear Inequalities Solving a linear inequality is basically like solving a linear equation. The only difference is that when you divide or multiply by a negative, you have to flip the symbol around. For example: -2x + 5 > 15 -2x > 10 x < 5

18. Quadratic Inequalities Quadratic inequalities are basically solved the same way quadratic equations are solved. For example: x^2 + 5x + 6 > 0 (x + 2)(x + 3) > 0 x + 2 > 0 x + 3 > 0 Solutions: x > -2 x > -3

19. Solving by Graphing Another way to solve any type of equation is to graph it. Generally, the easiest way to graph an equation/function is to first make a table. Then, just plot the points.

20. Solving by Graphing Continued Linear equations: Just make a table to gather a few points, then graph them. It should look like a straight line. From the graph you can find both the x and y intercepts. Quadratic equations: Just like for linear equations, make a table and plot a few points. It would also be beneficial to find the vertex. By looking at the graph you can find the x and y intercepts and if it is a maximum or a minimum. Solving a quadratic equation by graphing means looking for the zeros.

21. Solving by Graphing Continued Radical Equations: You can either make a table to gather several values or you can go from what you know about radical functions and just graph from there. (ie- √(x+5) just move to the left 5, and start curve on x-axis). Rational Equations: Again, you can either make a table or go off of what you already know about rational equations.

22. Solving by Graphing Continued Linear and Quadratic Inequalities: First make a table and graph the line/parabola as you would for a linear/quadratic equation. To decide where to shade plug in the point (0, 0). If the point works in the equation then shade on the side of the line/parabola that the point is on. If it does not work when you plug it in, shade on the opposite side where that point is not.