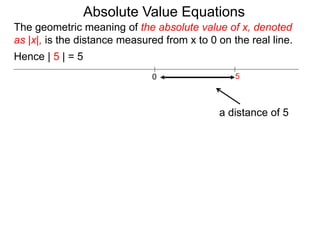
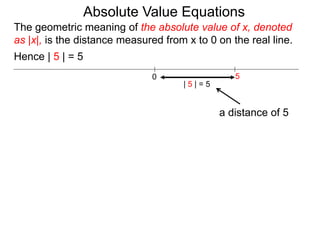
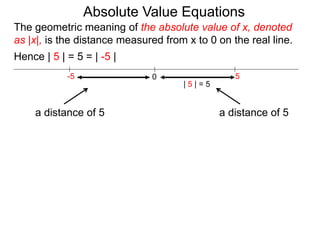
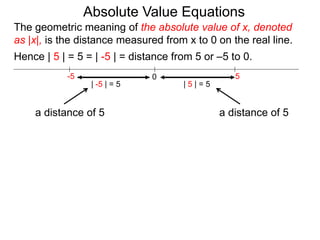
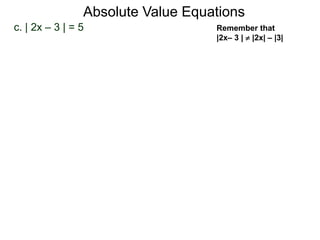The document discusses the definition and properties of absolute value equations. It defines absolute value as the distance from a number to zero on the real number line. It presents rules for solving absolute value equations, including rewriting an absolute value equation as two separate equations without the absolute value signs, and the property that if the absolute value of an expression is equal to a positive number a, then the expression must equal -a or a. Examples are provided to demonstrate solving absolute value equations using these rules and properties.

1. Absolute Value Equations

2. The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations

3. 0 5
Hence | 5 | = 5
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
a distance of 5
Absolute Value Equations

4. 0 5
Hence | 5 | = 5
| 5 | = 5
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
a distance of 5
Absolute Value Equations

5. The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
0 5-5
Hence | 5 | = 5 = | -5 |
| 5 | = 5
a distance of 5
Absolute Value Equations
a distance of 5

6. 0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
a distance of 5a distance of 5
Absolute Value Equations

7. 0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations

8. 0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations

9. |x|=
x if x is positive or 0.
{
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations

10. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations

11. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | =
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations

12. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5)
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.

13. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.

14. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.

15. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.

16. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|. For example, |–2*3 | = |–2|*|3| = 6.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.
Absolute Value Equations

17. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|. For example, |–2*3 | = |–2|*|3| = 6.
Warning: In general |x ± y|  |x| ± |y|.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.

18. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|. For example, |–2*3 | = |–2|*|3| = 6.
Warning: In general |x ± y|  |x| ± |y|.
For instance, |2 – 3 |  |2| – |3|  |2| + |3|.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
Absolute Value Equations
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.

19. |x|=
x if x is positive or 0.
–x (opposite of x) if x is negative.{
Hence | –5 | = –(–5) = 5.
Since the absolute value is never negative, an equation
such as |x14 – 3x9 + 1 | = –2 doesn't have any solution.
Fact I. |x*y| = |x|*|y|. For example, |–2*3 | = |–2|*|3| = 6.
Warning: In general |x ± y|  |x| ± |y|.
For instance, |2 – 3 |  |2| – |3|  |2| + |3|.
0 5-5
Hence | 5 | = 5 = | -5 | = distance from 5 or –5 to 0.
| -5 | = 5 | 5 | = 5
Because it is a distance measurement, |x| is nonnegative.
Algebraic definition of absolute value
The geometric meaning of the absolute value of x, denoted
as |x|, is the distance measured from x to 0 on the real line.
A “| |” can not be split
into two | |’s when
adding or subtracting.
Absolute Value Equations
Because –5 is negative,
use the 2nd part of the
rule and take its
opposite to obtain
its abs. value.

20. Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations.
Absolute Value Equations

21. Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
Absolute Value Equations

22. Fact II: If |#| = a, a >0, (where # is any expression)
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
Absolute Value Equations

23. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

24. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

25. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

26. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
–2x = –5 or –2x = 5
x = 5/2
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Dropping the “| |” and set the formula to 5 and –5.
Absolute Value Equations

27. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

28. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

29. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

30. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Dropping the “| |” and set the formula to 5 and –5.
Absolute Value Equations

31. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
–2x = –5 or –2x = 5
In picture, if | x | = 3 then
0 x = 3x = –3
Dropping the “| |” and set the formula to 5 and –5.
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Absolute Value Equations

32. Fact II: If |#| = a, a >0, (where # is any expression) then
# = –a or # = a.
Example A. Solve for x.
a. | x | = 3 then x = –3 or x = 3
b. | –2x | = 5
–2x = –5 or –2x = 5
x = –5/2So x = 5/2
In picture, if | x | = 3 then
0 x = 3x = –3
Because |x±y|  |x|±|y|, many steps for solving regular
equations are not valid for | |-equations. We have to solve an
| |-equation by rephrasing it into two equations without the | |.
0 a–a
Dropping the “| |” and set the formula to 5 and –5.
Absolute Value Equations

33. c. | 2x – 3 | = 5
Absolute Value Equations

34. c. | 2x – 3 | = 5
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|

35. c. | 2x – 3 | = 5
Drop the “| |”.
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|

36. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
Drop the “| |”. Settings
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|

37. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = –2
Drop the “| |”. Settings
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|

38. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = –2
x = –1
Drop the “| |”. Settings
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

39. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 82x = –2
x = –1
Drop the “| |”. Settings
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

40. c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

41. d. | 2 – 3x | + 2 = 4
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

42. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

43. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

44. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

45. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

46. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |.
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

47. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |. Settings
2 – 3x = 22 – 3x = –2 or
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

48. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |. Settings
2 – 3x = 22 – 3x = –2
–3x = –4
or
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So

49. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |. Settings
2 – 3x = 22 – 3x = –2
–3x = –4
or
x = 4/3
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So
So

50. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |. Settings
2 – 3x = 22 – 3x = –2
–3x = 0–3x = –4
or
x = 4/3
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
So
So

51. d. | 2 – 3x | + 2 = 4
We have to isolate the | |-term before the dropping the “| |”.
| 2 – 3x | + 2 = 4
| 2 – 3x | = 2
Drop the | |. Settings
2 – 3x = 22 – 3x = –2
–3x = 0–3x = –4
or
x = 4/3
c. | 2x – 3 | = 5
2x – 3 = –5 or 2x – 3 = 5
2x = 8
x = 4
2x = –2
x = –1
Drop the “| |”. Settings
Incorrect versions:
2–3x+2=–4 or 2–3x+2=4
Absolute Value Equations
Remember that
|2x– 3 |  |2x| – |3|
x = 0So
So

52. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|.
Absolute Value Equations

53. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”.
Absolute Value Equations
yx |x – y| = |y – x|

54. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
yx
same distance
|x – y| = |y – x|

55. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9|
yx
same distance
|x – y| = |y – x|

56. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
yx
same distance
|x – y| = |y – x|

57. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance
|x – y| = |y – x|

58. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
Example B. Solve for x geometrically if |x – 7| = 12.
yx
same distance
|x – y| = |y – x|

59. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
Example B. Solve for x geometrically if |x – 7| = 12.
We want the locations of x's that are 12 units away from 7.
yx
same distance
|x – y| = |y – x|

60. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
Example B. Solve for x geometrically if |x – 7| = 12.
We want the locations of x's that are 12 units away from 7.
7
1212
x x
yx
same distance
|x – y| = |y – x|

61. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance
Example B. Solve for x geometrically if |x – 7| = 12.
We want the locations of x's that are 12 units away from 7.
7
1212
x = – 5 x
So to the left x = 7 – 12 = – 5,
|x – y| = |y – x|

62. The geometric meaning of | x | as “distance from 0 and x” may
be extended to the meaning for |x – y|. The geometric meaning
of |x – y| = |y – x| = “distance between x and y”. Note the two
versions reflect that “distance” is always mutual in the sense
that “going from x to y” is as much as “going from y to x”.
Absolute Value Equations
|9 – 3| = 6 = |3 – 9| and |(–8) – (–1)| = 7.
We can solve for x using this method.
yx
same distance
Example B. Solve for x geometrically if |x – 7| = 12.
We want the locations of x's that are 12 units away from 7.
7
1212
x = 19
So to the left x = 7 – 12 = – 5, and to the right x = 7 + 12 = 19.
|x – y| = |y – x|
x = – 5

63. The rule for dropping the | | extends to the following setups.
Absolute Value Equations

64. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
The rule for dropping the | | extends to the following setups.
Absolute Value Equations

65. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Absolute Value Equations
The rule for dropping the | | extends to the following setups.

66. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
a. |2x – 3| = |3x + 1|
Absolute Value Equations
The rule for dropping the | | extends to the following setups.

67. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
a. |2x – 3| = |3x + 1|
Absolute Value Equations
The rule for dropping the | | extends to the following setups.

68. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
Absolute Value Equations
The rule for dropping the | | extends to the following setups.

69. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
–1 – 3 = 3x – 2x
Absolute Value Equations
The rule for dropping the | | extends to the following setups.

70. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
–1 – 3 = 3x – 2x
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

71. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
2x – 3 = –3x – 1–1 – 3 = 3x – 2x
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

72. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
2x – 3 = –3x – 1–1 – 3 = 3x – 2x
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

73. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
2x – 3 = –3x – 1
x = 2/5
–1 – 3 = 3x – 2x
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

74. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
b. |x – 1| = |x + 1|
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
2x – 3 = –3x – 1
x = 2/5
–1 – 3 = 3x – 2x
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

75. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
b. |x – 1| = |x + 1|
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
2x – 3 = –3x – 1
x = 2/5
Dropping the “| |” and set
–1 – 3 = 3x – 2x
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

76. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
b. |x – 1| = |x + 1|
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
2x – 3 = –3x – 1
x = 2/5
Dropping the “| |” and set
x – 1 = x + 1
–1 – 3 = 3x – 2x
x – 1 = –(x + 1)or
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

77. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
b. |x – 1| = |x + 1|
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
2x – 3 = –3x – 1
x = 2/5
Dropping the “| |” and set
x – 1 = x + 1
0 = 2
–1 – 3 = 3x – 2x
x – 1 = –(x + 1)or
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

78. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
b. |x – 1| = |x + 1|
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
x – 1 = –(x + 1)
2x – 3 = –3x – 1
x = 2/5
Dropping the “| |” and set
orx – 1 = x + 1
0 = 2
–1 – 3 = 3x – 2x
Impossible!
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

79. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
b. |x – 1| = |x + 1|
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
x – 1 = –(x + 1)
2x – 3 = –3x – 1
x = 2/5
Dropping the “| |” and set
orx – 1 = x + 1
x – 1 = –x – 10 = 2
–1 – 3 = 3x – 2x
Impossible!
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

80. Fact III: If |E1| = |E2| where E1, E2 are two expressions,
then E1 = E2 or E1 = –(E2).
Example C. Solve for x.
Dropping the “| |” and set
–4 = x 5x = 2
b. |x – 1| = |x + 1|
a. |2x – 3| = |3x + 1|
2x – 3 = 3x + 1 or 2x – 3 = –(3x + 1)
x – 1 = –(x + 1)
2x – 3 = –3x – 1
x = 2/5
Dropping the “| |” and set
orx – 1 = x + 1
x – 1 = –x – 1
2x = 0 x = 0
0 = 2
–1 – 3 = 3x – 2x
Impossible!
Absolute Value Equations
The rule for dropping the | | extends to the following setups.
So

81. Ex. A.
1. Is it always true that I+x| = x? Give reason for your answer.
2. Is it always true that |–x| = x? Give reason for your answer.
Absolute Value Equations
Ex. B. Drop the | | and write the problem into two equations
then solve for x (if any) and label the answer(s) on the real
line.
3. |x| = 2 4. |x| = 5 5. |–x| = 2 6. |–x| = 5
7. |x| = –2 8. |–2x| = 6 9. |–3x| = 6 10. |–x| = –5
11. |3 – x| = –5 12. |3 + x| = 7 13. |x – 9| = 5
14. |5 – x| = 5 15. |4 + x| = 9 16. |2x + 1| = 3
17. |4 – 5x| = 3 18. |3 + 2x| = 7 19. |–2x + 3| = 5
20. |4 – 5x| = –3 21. |2x + 1| – 1= 5 21. 3|2x + 1| – 1= 5

82. Absolute Value Equations
Ex. C. Solve for x by using the geometric method.
28. |4 – 5x| = |3 + 2x|
30. |4 – 5x| = |2x + 1| 31. |3x + 1| = |5 – x|
22. |x – 2| = 1 23. |3 – x| = 5 24. |x – 5| = 5
25. |7 – x| = 3 26. |8 + x| = 9 27. |x + 1| = 3
Ex. D. Drop the | | then solve for x.
29. |–2x + 3|= |3 – 2x|
32. |3 – 2x| = |2x + 1| 33. |3x + 1| = |–3x – 1|