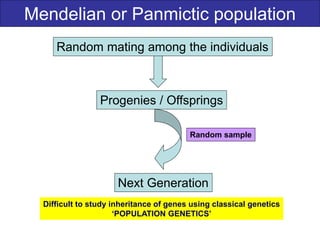
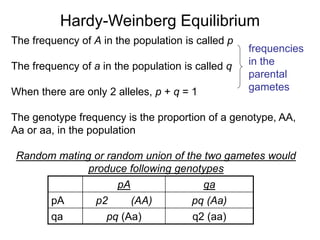
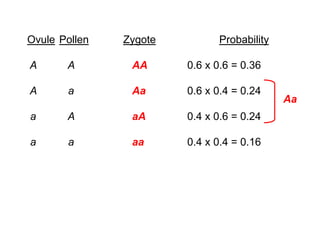
1) The document discusses Hardy-Weinberg equilibrium, which states that allele and genotype frequencies in a population remain constant from generation to generation if the population is large, randomly mating, and not experiencing selection, migration, mutation or genetic drift. 2) It provides an example showing how the frequencies of genotypes AA, Aa and aa are calculated based on the allele frequencies p and q in the parental generation. 3) The document explains that under Hardy-Weinberg equilibrium, the allele frequencies p and q will remain the same in subsequent generations, even as the specific genotype frequencies may change during mating.

1. Dr. NAVEENKUMAR K.L
Assistant Professor
Dept. Genetics and Plant Breeding
Breeding of Cross Pollinated Crops

2. Genetic composition of cross pollinated crops
• Highly heterozygous – Random mating population
Random mating – Each individual of the population
has equal chance of mating with any other
individual of that population
Population – individuals that share the same gene pool
Gene pool – The sum total of all the genes present in
a population

3. Mendelian or Panmictic population
Random mating among the individuals
Progenies / Offsprings
Random sample
Next Generation
Difficult to study inheritance of genes using classical genetics
‘POPULATION GENETICS’

4. Hardy-Weinberg Law
• Independently developed by Hardy (1908)
in England and Weinberg (1909) in
Germany.
The law states that,
“In a large random mating population gene and
genotypic frequency remains constant generation after
generation in absence of selection, mutation, migration
or random drift”

5. Assume a population where there are two alleles of a gene,
A and a
- frequency of allele A in the gene pool is 60%, or 0.6
- in other words, 60% of gametes produced by plants in this
population carry the A allele
- frequency of allele a in the gene pool is 40%, or 0.4
There would be three genotypes AA, Aa & aa possible for this
gene in the population
Population Genetics

6. What will be the frequencies of the various genotypes
(AA, Aa, aa) after one round of random mating?
Chance that an A pollen will fertilize an A ovule:
(frequency of X (frequency of = frequency of
A pollen) A ovule) AA zygote
0.6 X 0.6 = 0.36

7. Ovule Pollen Zygote Probability
A A AA 0.6 x 0.6 = 0.36
A a Aa 0.6 x 0.4 = 0.24
a A aA 0.4 x 0.6 = 0.24
a a aa 0.4 x 0.4 = 0.16
Aa

8. 0.36 + 0.48 + 0.16 = 1 These probabilities are the genotype
AA Aa aa frequencies of the next generation
So what will the allele frequencies be after this generation
reproduces? (will the frequencies change?)
Calculate new gamete frequencies, as before:
AA is 36% of the population (0.36), so 36% of gametes are A
Aa is 48% of the population, so 24% of gametes are A and
24% are a
aa is 16% of the population, so 16% of gametes are a
New allele frequencies:
A: 0.36 + 0.24 = 0.6
a: 0.24 + 0.16 = 0.4

9. The allele frequencies for the A and a alleles do not change
from generation to generation
- they are in equilibrium 0.6 (A) + 0.4 (a) = 1
- hence, the population does not evolve
This illustrates an example that is true in general:
allele frequencies do not change from generation to
generation
Gene frequency is the proportion of an allele A or a, in a
random mating population
i.e., gametes carrying A or a is known as gene frequency
Hardy-Weinberg Equilibrium

10. The frequency of A in the population is called p
The frequency of a in the population is called q
When there are only 2 alleles, p + q = 1
The genotype frequency is the proportion of a genotype, AA,
Aa or aa, in the population
Random mating or random union of the two gametes would
produce following genotypes
frequencies
in the
parental
gametes
Hardy-Weinberg Equilibrium
pA qa
pA p2 (AA) pq (Aa)
qa pq (Aa) q2 (aa)

11. AA Aa aa
p x p (p x q) + (q x p) q x q
p2 2pq q2
so, we’ve gone from allele frequencies in the parental gene pool
to genotype frequencies among the offspring
What happens when these offspring reproduce?…
Calculate new gamete frequencies, as before:
AA has frequency = p2, so p2 gametes will carry the A allele
Aa has frequency = 2pq, so ½ (2pq) or pq gametes will carry A
Hardy-Weinberg Equilibrium

12. Aa has a frequency = 2pq, so ½ (2pq) or pq gametes will carry A
Aa has a frequency = 2pq, so ½ (2pq) or pq gametes will carry a
New allele frequency:
A: p2+ pq
The frequency of A can be re-stated as:
p2 + pq = p(p + q) Since p + q = 1
= p(1)
= p
Hardy-Weinberg Equilibrium

13. Thus, we can draw 2 conclusions from the Hardy-Weinberg
equilibrium principle:
#1) frequency of an allele stays the same over generations
- it doesn’t matter what the particular allele frequencies are
- it doesn’t matter how many alleles there are for a gene
#2) when allele frequencies are given as p and q,
the genotype frequencies will be:
p2 + 2pq + q2
The Hardy-Weinberg principle predicts that evolution will not
happen in a population -- unless one of the underlying
4 assumptions is violated
Hardy-Weinberg Equilibrium

14. Factors affecting equilibrium
1) Selection
- all individuals survive and reproduce equally
- if individuals of some genotypes survive and reproduce
more than others, then allele frequencies may change
from one generation to the next
2) Mutation
- It may produce a new allele not present in the population
or may change the frequencies of existing allele
Hardy-Weinberg Assumptions

15. Factors affecting equilibrium
3) Migration
- Movement of individuals into a population from a
different population
- if individuals with certain genotypes leave the
population, then the allele frequencies may change
4) Random drift
- is a random change in gene frequency due to
sampling error
- commonly happens in small populations
- genetic drift causes evolution by changing allele
frequencies
Hardy-Weinberg Assumptions