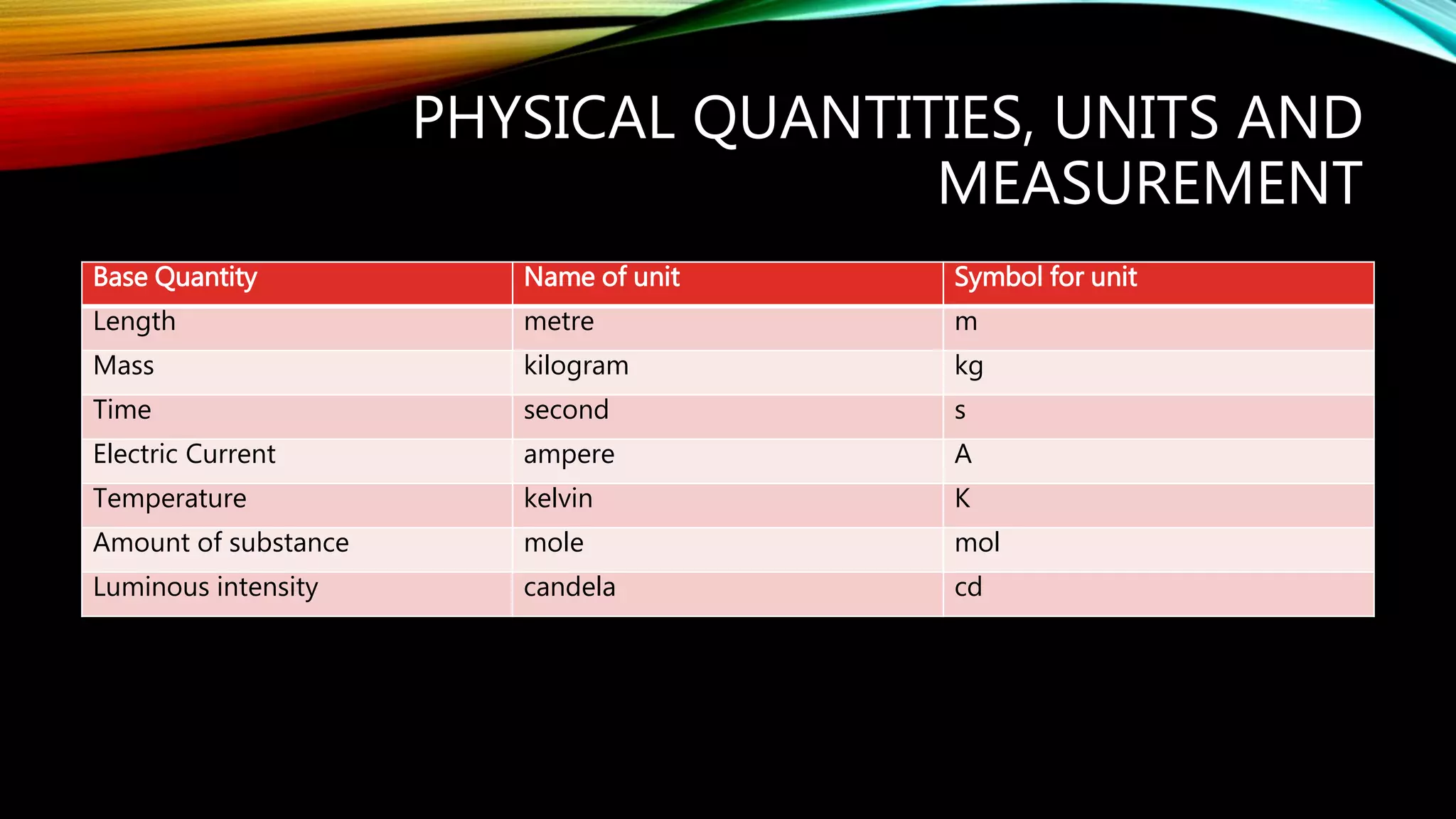
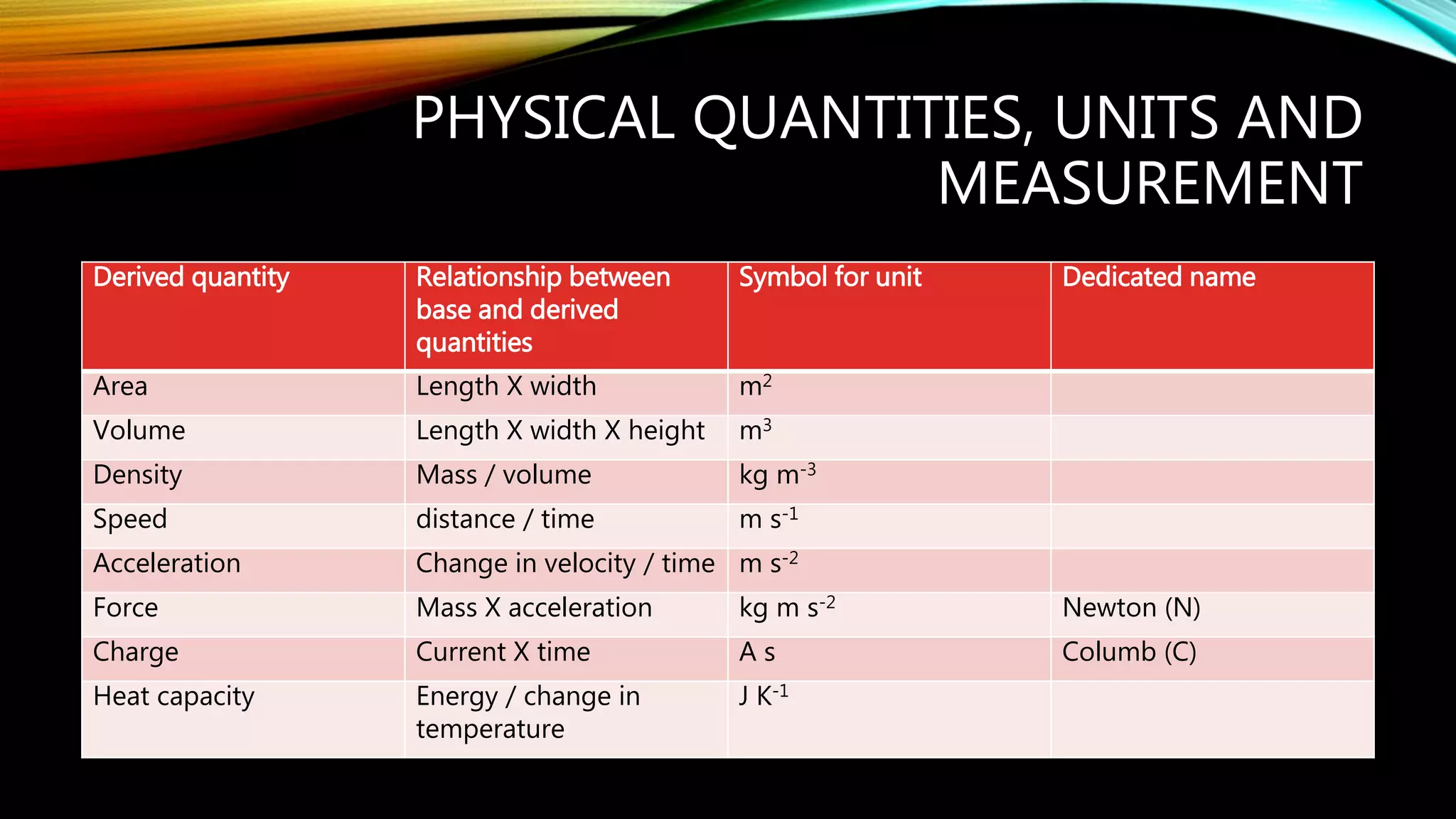
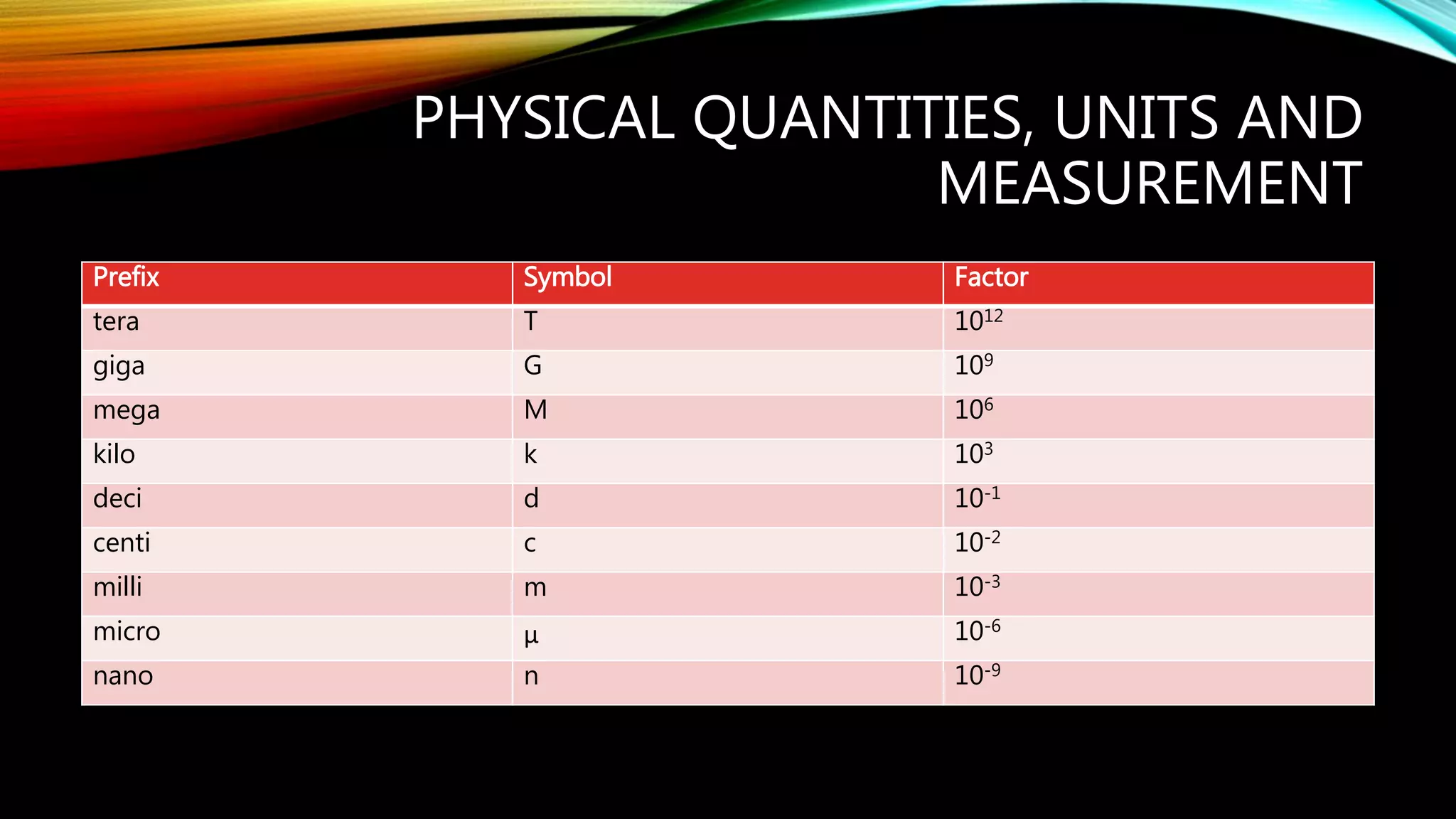
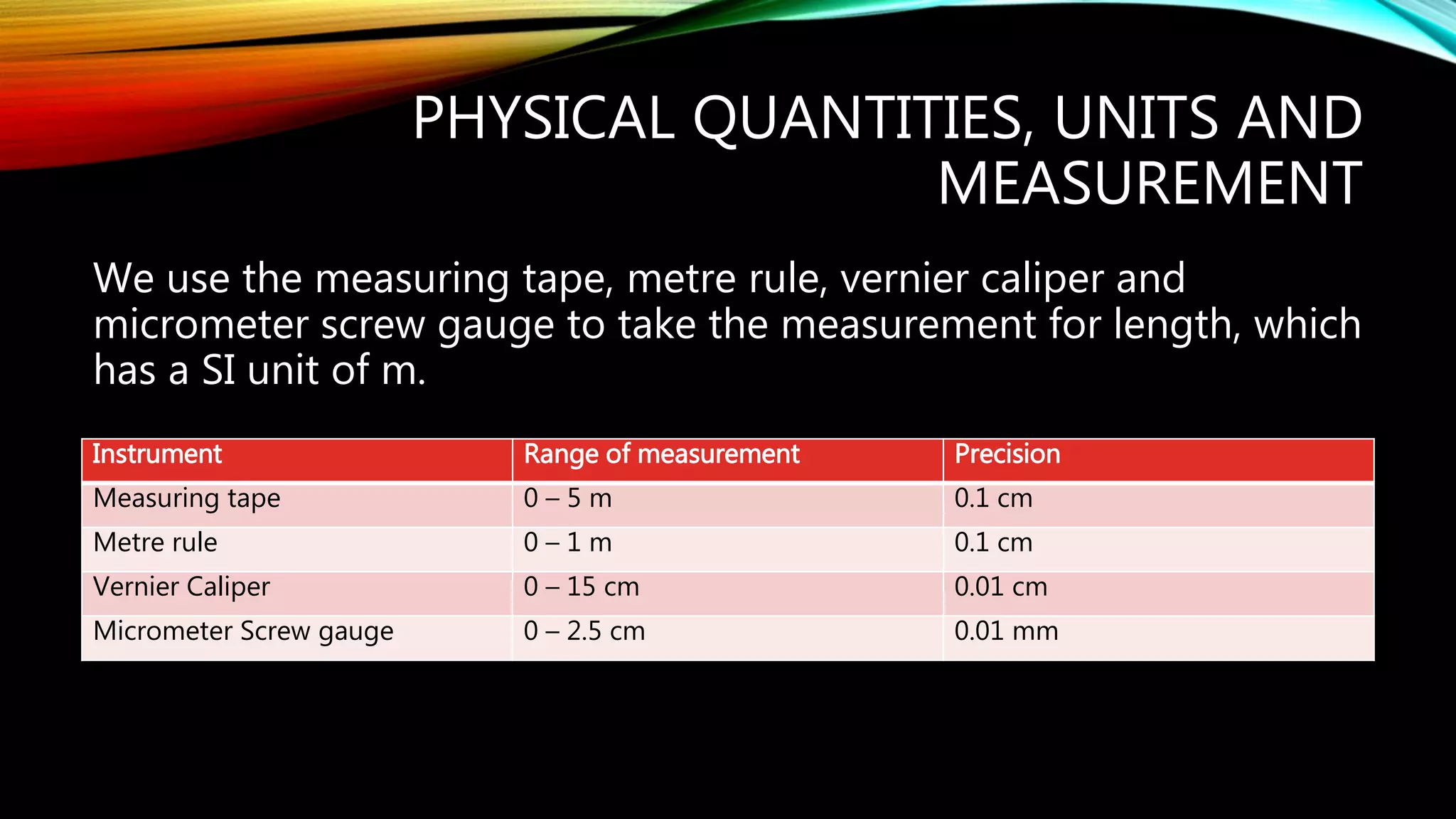
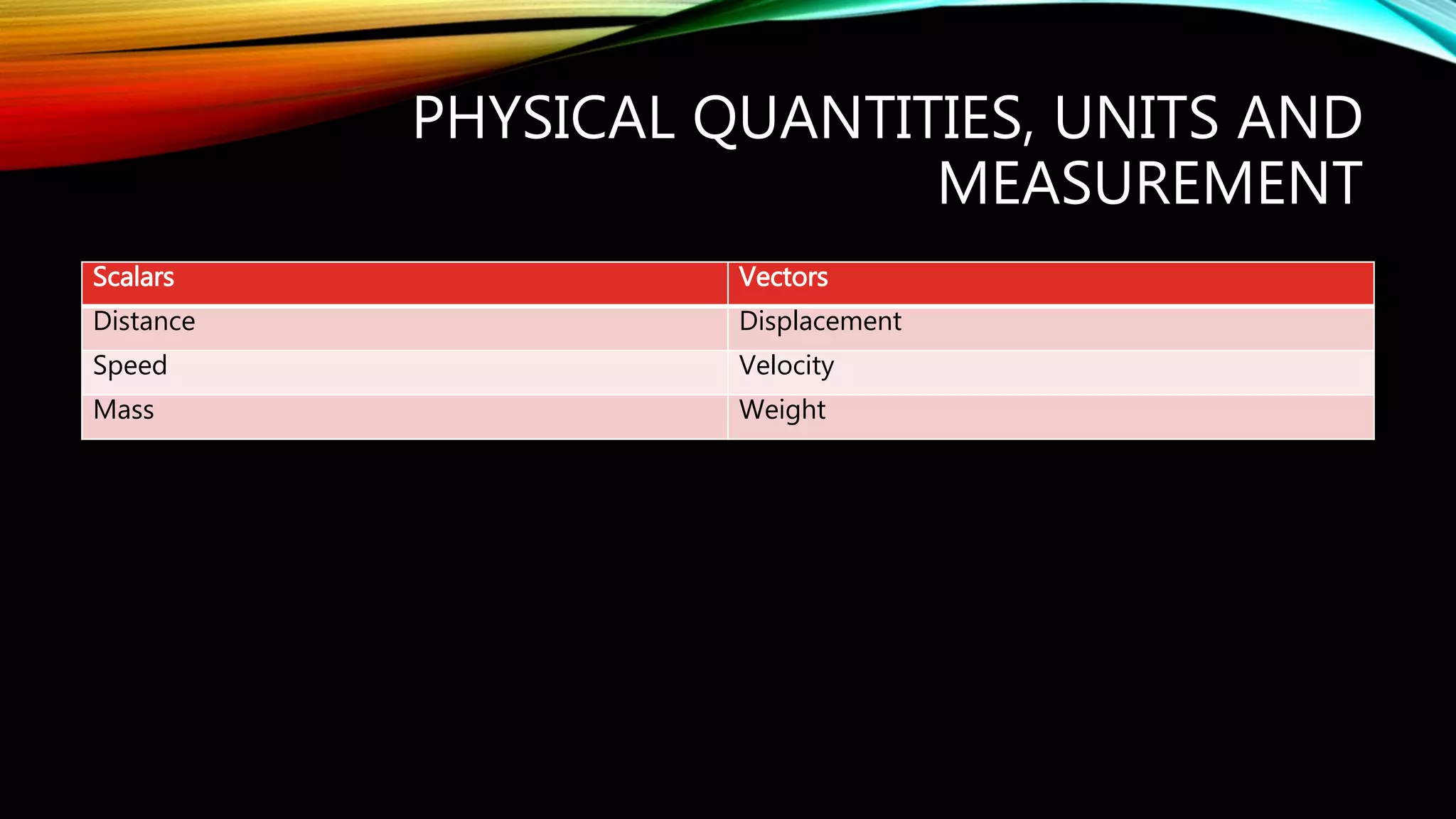
The document describes physical quantities and their measurement, outlining base and derived units, common instruments for measurement, and types of errors that can occur. It distinguishes between scalar and vector quantities and explains how to correctly add them while considering direction. Additionally, it provides examples of adjustments needed for zero errors in measurements.

1. PHYSICAL QUANTITIES, UNITS
AND MEASUREMENT

2. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
A physical quantity is a quantity that can be measured and consists
of a numerical magnitude and unit.

3. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Base Quantity Name of unit Symbol for unit
Length metre m
Mass kilogram kg
Time second s
Electric Current ampere A
Temperature kelvin K
Amount of substance mole mol
Luminous intensity candela cd

4. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
The units of any particular physical quantity can be derived
according to base units involved.

5. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Derived quantity Relationship between
base and derived
quantities
Symbol for unit Dedicated name
Area Length X width m2
Volume Length X width X height m3
Density Mass / volume kg m-3
Speed distance / time m s-1
Acceleration Change in velocity / time m s-2
Force Mass X acceleration kg m s-2 Newton (N)
Charge Current X time A s Columb (C)
Heat capacity Energy / change in
temperature
J K-1

6. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
To handle huge numbers easily, we use prefixes to simplify the
writing of such numbers.

7. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Prefix Symbol Factor
tera T 1012
giga G 109
mega M 106
kilo k 103
deci d 10-1
centi c 10-2
milli m 10-3
micro μ 10-6
nano n 10-9

8. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
When taking measurements using tools and apparatus, it is quite
common to experience errors. There are two kinds of errors:
Random error
Systematic error

9. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Random errors arises when observers estimate the last figure of a
reading on an instrument. Usually affected due to reaction time,
background noises or vibrations.
To reduce such errors, we usually take a large number of readings
and obtain the average. Any distinct abnormally is usually excluded
in the calculation of the average.

10. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Systematic errors are constant errors in taking measurements. This
will usually cause consistent underestimate or overestimate of a
reading. Systematic errors can be due to faulty equipment or
apparatus such as zero error.
Unlike random errors, systematic errors cannot be reduced by using
the averaging method, but instead eliminate the sources of the
errors or doing some adjustments to the measurements.

11. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
We use the measuring tape, metre rule, vernier caliper and
micrometer screw gauge to take the measurement for length, which
has a SI unit of m.
Instrument Range of measurement Precision
Measuring tape 0 – 5 m 0.1 cm
Metre rule 0 – 1 m 0.1 cm
Vernier Caliper 0 – 15 cm 0.01 cm
Micrometer Screw gauge 0 – 2.5 cm 0.01 mm

12. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
When using the measuring tape and metre rule, we should be
careful to avoid parallax error by positioning our eye so that the
line of sight is at right angle to the scale.
When using the vernier caliper and micrometer screw gauge, we
should be careful to avoid zero error by ensuring the initial
readings starts at zero.

13. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
You have a positive zero error when the instrument measures a
certain positive length before taking measurements. We will make
adjustments by taking the final length to minus the initial length.
Conversely, you have a negative zero error when the instrument
measures a certain negative length before taking measurements.
We will make adjustments by taking the final length to minus the
initial negative length.

14. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Positive error example:
The vernier caliper measures 0.1 cm when closed.
We measure the diameter of a nut and the observed reading is 3.25
cm
Adjustment: 3.25 cm – 0.1 cm = 3.15cm
Diameter of the nut = 3.15 cm

15. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Negative zero error example:
The micrometer screw gauge measures -0.04mm when closed.
We measure the the diameter of a screw and the observed reading
is 4.16 mm
Adjustment: 4.16 – (- 0.04) = 4.20 mm
Diameter of the screw = 4.20 mm

16. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
We use the stopwatch to measure short intervals of time. The
digital stopwatches are more common these days and have a
accuracy to 0.01s.
One possible reason for errors in time taking using the stopwatch is
due to our reaction time.

17. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Scalar quantities are quantities that have magnitude only.
Vector quantities are quantities that have both magnitude and
direction

18. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Scalars Vectors
Distance Displacement
Speed Velocity
Mass Weight

19. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Addition of scalars are straightforward. Just simply add up the
numbers.
Addition of vectors are slightly different, as we need to consider the
direction of the vectors.

20. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
5N
5N
Resultant force = 5N + 5N = 10N to the right

21. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
5N 5N
Resultant force = 5N - 5N = 0

22. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
5N
Resultant force = 10N + 5N = 15N to the right
10N

23. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
5N
Resultant force = 10N - 5N = 5N to the left
10N

24. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
We can also solve forces at an angle to each other using the
parallelogram method.

25. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
A
B
Resultant force

26. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Alternatively, we can use the vector triangle method (tail to head,
head to tail method).

27. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
Resultant force

28. PHYSICAL QUANTITIES, UNITS AND
MEASUREMENT
The End