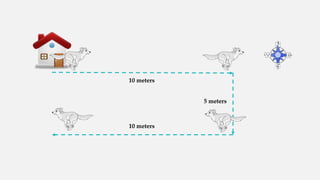
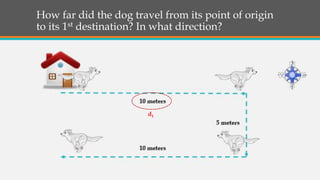
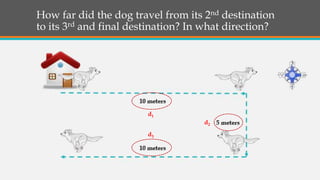
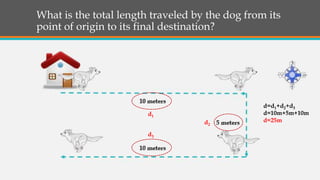
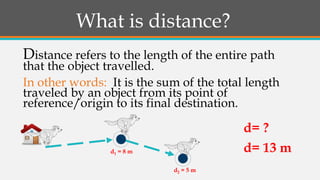
The document discusses the differences between distance and displacement in motion. Distance refers to the total length traveled between two points, regardless of path, while displacement is the shortest distance between the initial and final positions. Several examples are given to demonstrate how to calculate total distance and displacement. The key difference is that displacement considers direction, making it a vector quantity, while distance does not and is simply a magnitude. 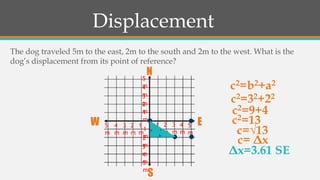The document then provides a quiz to test understanding of distance vs displacement. Examples are worked out to find the total distance traveled and displacement in different scenarios involving an object moving in various directions. The Pythagorean theorem is applied to solve for displacement.

1. Distance &
Displacement
Measures of Motion

2. 10 meters
10 meters
5 meters

3. How far did the dog travel from its point of origin
to its 1st destination? In what direction?
d1

4. How far did the dog travel from its 1st destination to
its 2nd destination? In what direction?
d1
d2

5. How far did the dog travel from its 2nd destination
to its 3rd and final destination? In what direction?
d1
d2
d3

6. What is the total length traveled by the dog from its
point of origin to its final destination?
d1
d2
d3
d=d1+d2+d3
d=10m+5m+10m
d=25m

7. What is the shortest distance of the dog relative to
its points of origin?
d1
d2
d3
d=d1+d2+d3
d=10m+5m+10m
d=25m
Δx=5m South

8. What is distance?
Distance refers to the length of the entire path
that the object travelled.
In other words: It is the sum of the total length
traveled by an object from its point of
reference/origin to its final destination.
d1 = 8 m
d2 = 5 m
d= ?
d= 13 m

9. What is displacement?
Displacement refers to the shortest
distance between the object’s two
positions, like the distance between its
point of origin and its point of
destination, no matter what path it
took to get to that destination.

10. Displacement
d1
d2
d3
d=d1+d2+d3
d=10m+5m+10m
d=25m
Δx=5m South

11. Displacement
5 meters
2 meters
2 meters
Δx=?

12. Displacement
Δx=?
PYTHAGOREAN THEOREM
FOR ANY RIGHT TRIANGLE, THE SQUARE OF
THE HYPOTENUSE IS EQUAL TO THE SUM OF
THE SQUARES OF THE OTHER TWO SIDES
c2=b2+a2

13. PYTHAGOREAN THEOREM
FOR ANY RIGHT TRIANGLE, THE SQUARE OF THE HYPOTENUSE IS
EQUAL TO THE SUM OF THE SQUARES OF THE OTHER TWO SIDES
c2=b2+a2
90°
a
b
c

14. Displacement
5 meters
2 meters
2 meters
What is the dog’s
displacement from its
point of reference?

15. Displacement
The dog traveled 5m to the east, 2m to the south and 2m to the west. What is the
dog’s displacement from its point of reference?
N
S
E
W 4
m
5
m
1
m
2
m
3
m
5
m
4
m
3
m
2
m
1
m
1
m
3
m
2
m
4
m
5
m
5
m
3
m
4
m
2
m
1
m
c2=b2+a2
a
b
c
c2=32+22
c2=9+4
c2=13
c=√13
Δx=3.61 SE
c= Δx

16. Distance & Displacement
The dog traveled 3m west, 4m to the north and 4m to the east. What is the dog’s
displacement from its point of reference? What is the total distance traveled?
N
S
E
W 4
m
5
m
1
m
2
m
3
m
5
m
4
m
3
m
2
m
1
m
1
m
3
m
2
m
4
m
5
m
5
m
3
m
4
m
2
m
1
m
c2=b2+a2
a
b
c
c2=12+42
c2=1+16
c2=17
c=√17
Δx=4.12m NE
c= Δx
d= d1+d2+d3
d= 3+4+4
d= 11 m

17. COMPARISON
DISTANCE DISPLACEMENT
Distance is the length of the path
travelled by an object from an initial
position to the final position.
Displacement is the shortest distance
between the point of reference to the
final position of the body regardless of
the path it took to get to that final path.
It is a scalar quantity containing
magnitude only. Ex. 30 m
It is a vector quantity containing both
magnitude and direction. Ex. 30m East
There is always distance covered
whenever there is motion.
Displacement will be zero if the object
comes back to its initial position.
Distance is always greater than
displacement.
Displacement is always lesser than or
equal to distance.

18. Why do we study distance and displacement?

19. Now you are ready
for a short quiz! 

20. 1. Distance is a vector quantity.
a.True
b.False
c. Partially true
d.None of the above.

21. 2. Can displacement be greater
than distance?
a.No, it can be shorter but it
cannot be greater than distance.
b.Yes, it can be greater than
distance.
c. It depends on the given
parameters.
d. None of the above.

22. 3. “Displacement is equal to zero if the
object traveled back to its initial point of
origin.” The statement is…
a.False
b.Partially false
c. True
d.None of the above

23. 4-5. A student walks 2 m east, 4 m north
and 6 m west. Solve for distance and
displacement.

24. 1. Distance is a vector quantity.
a.True
b.False
c. Partially true
d.None of the above.

25. 2. Can displacement be greater
than distance?
a.No, it can be shorter but it
cannot be greater than distance.
b.Yes, it can be greater than
distance.
c. It depends on the given
parameters.
d. None of the above.

26. 3. “Displacement is equal to zero if the
object traveled back to its initial point of
origin.” The statement is…
a.False
b.Partially false
c. True
d.None of the above

27. 4-5. A student walks 2 m east, 4 m
north and 6 m west. Solve for distance
and displacement.
d=d1+d2+d3
d=2+4+6
d=12 m
c2=b2 + a2
c2=42+42
c2=16+16
c2=32
c=√32
Δx=5.66m NW

28. Distance & Displacement
4-5. A student walks 2 m east, 4 m north and 6 m west. Solve for distance and
displacement.
N
S
E
W 4
m
5
m
1
m
2
m
3
m
5
m
4
m
3
m
2
m
1
m
1
m
3
m
2
m
4
m
5
m
5
m
3
m
4
m
2
m
1
m
c2=b2+a2
a
b
c
c2=42+42
c2=16+16
c2=32
c=√32
Δx=5.66m NW
c= Δx
d= d1+d2+d3
d= 2+4+6
d= 12 m

29. HOMEWORK:
In your assignment notebook, define the
following:
1.Speed
2.Velocity