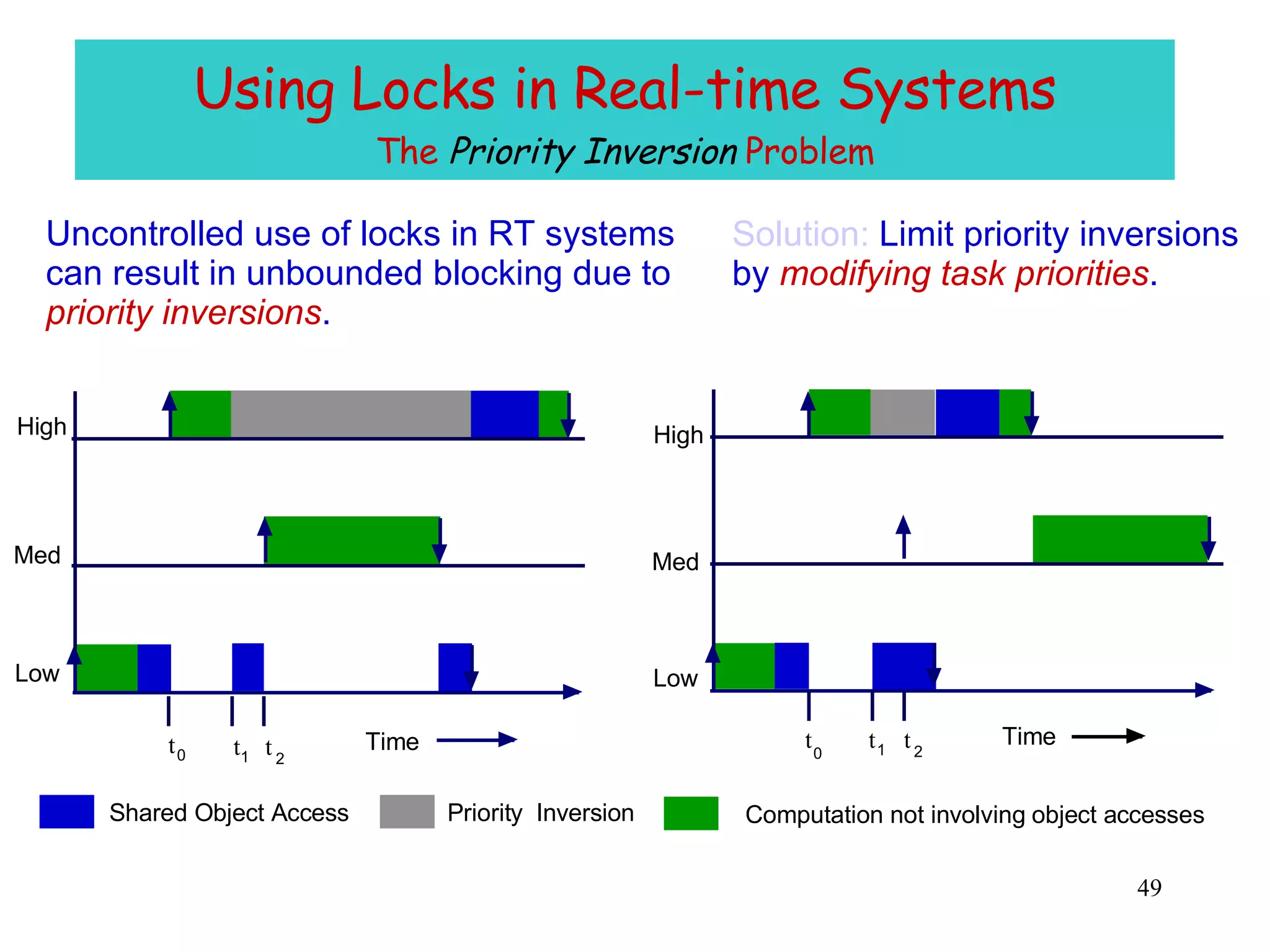
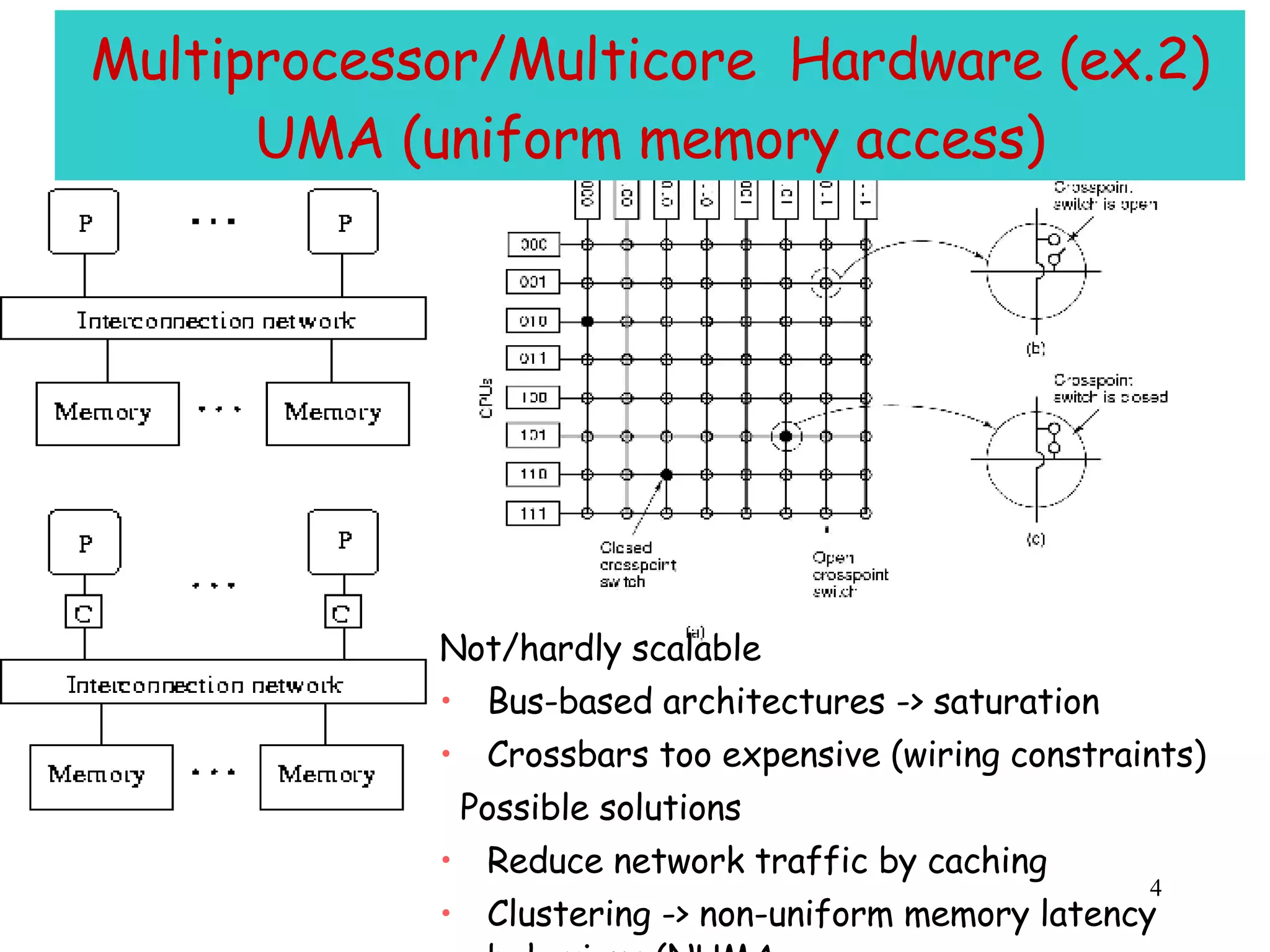
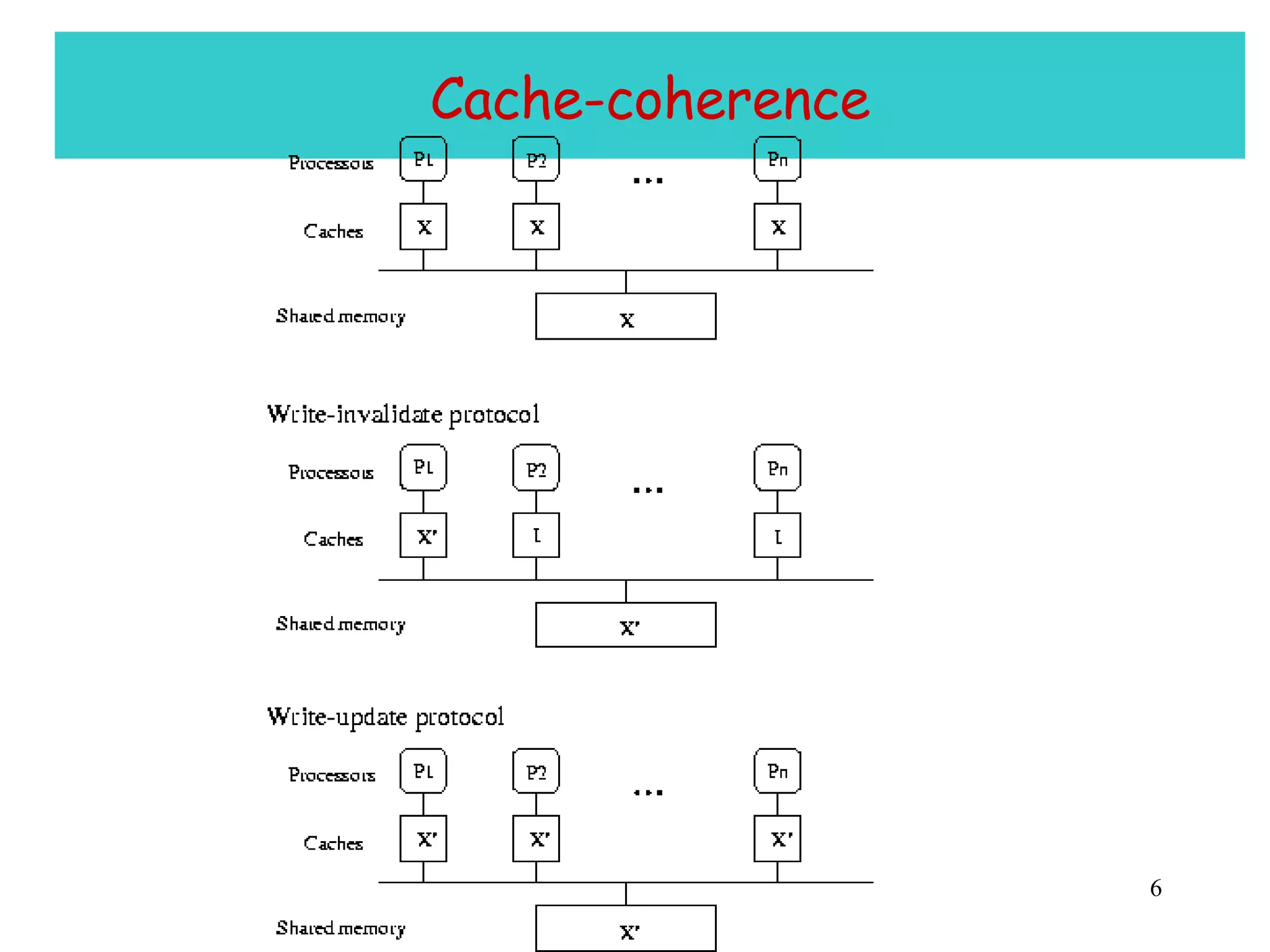
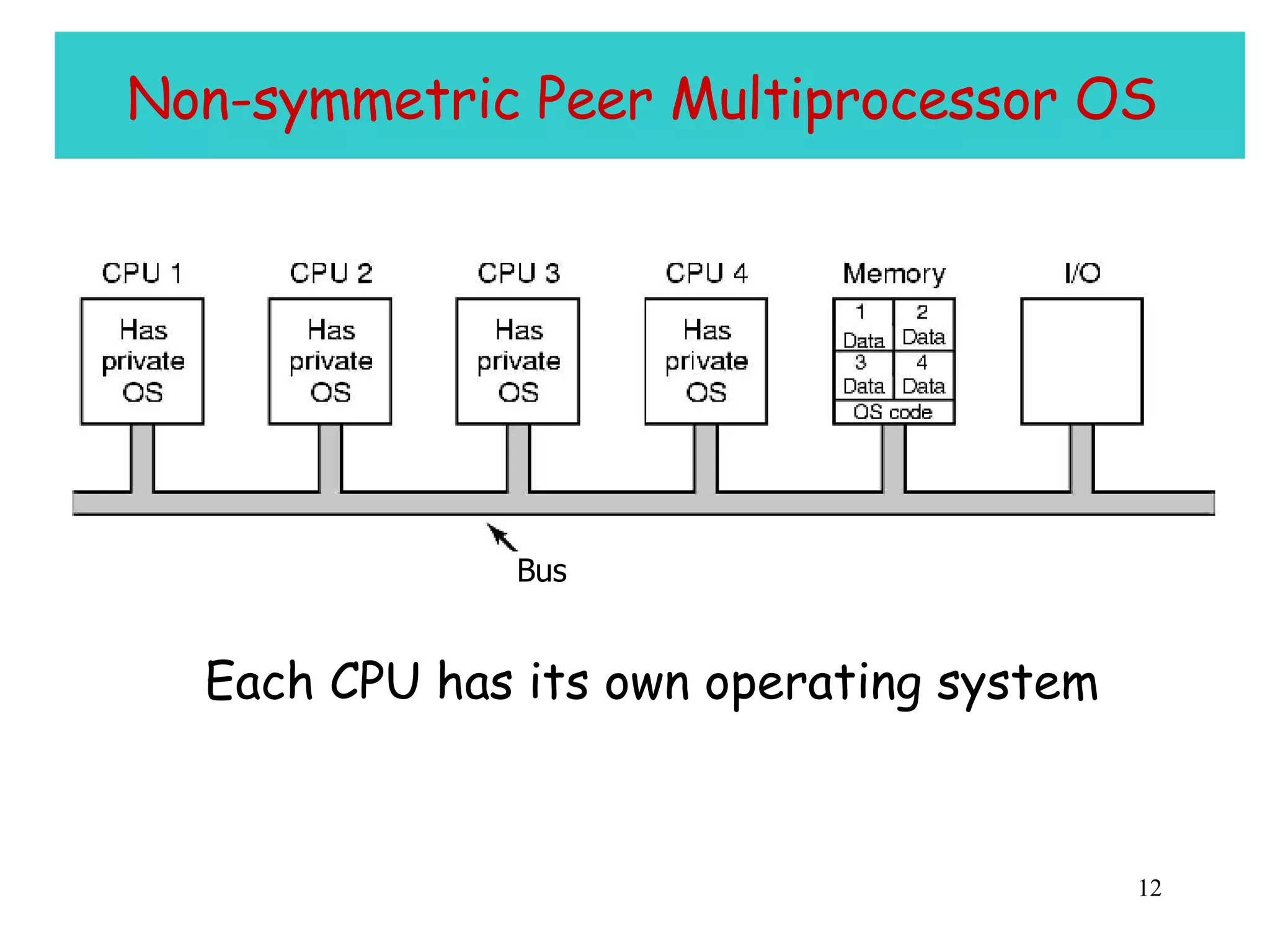
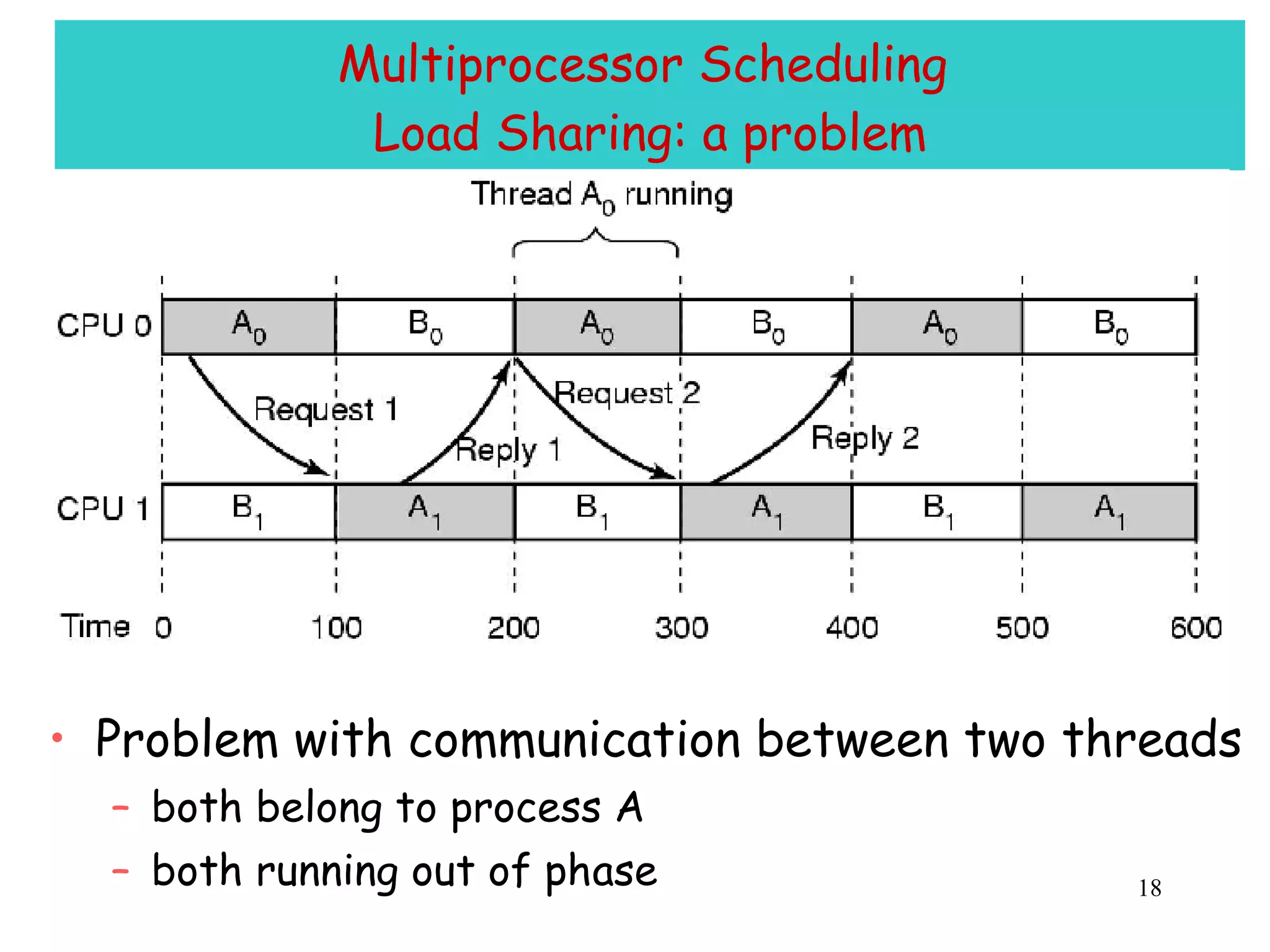
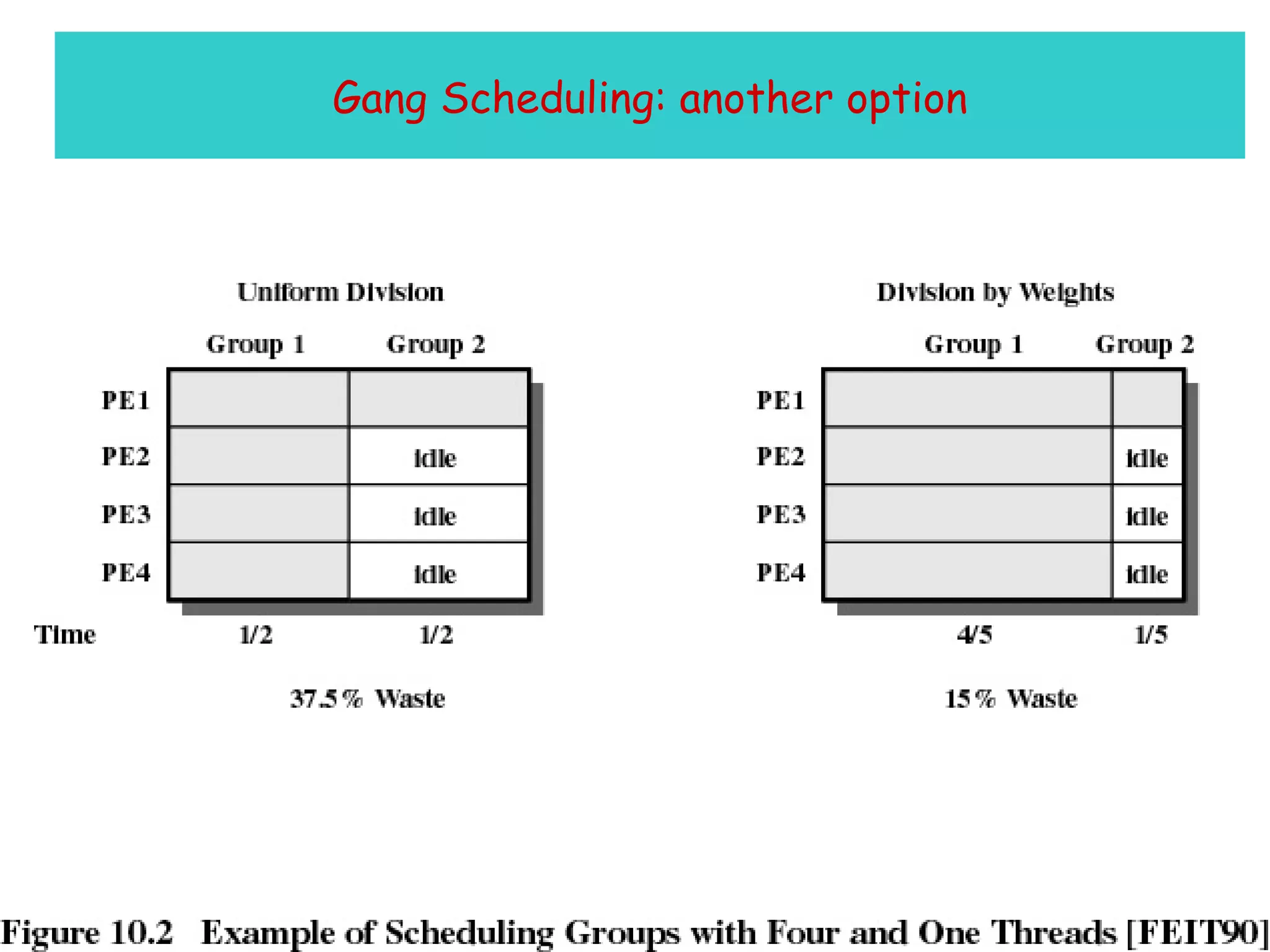
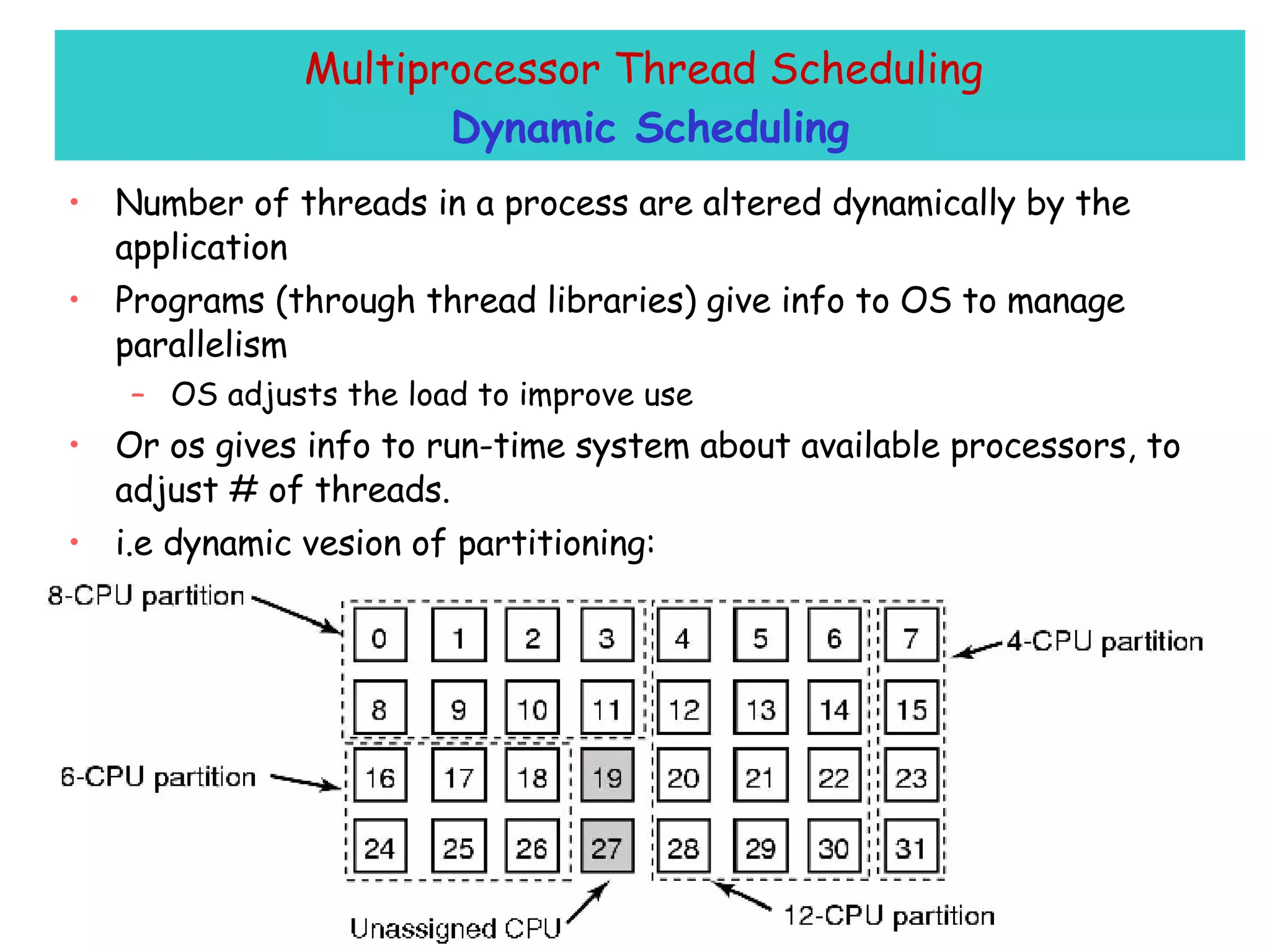
The document discusses multiprocessor and multicore systems. It defines multiprocessors as systems with two or more CPUs sharing full access to common RAM. It describes different hardware architectures for multiprocessors like bus-based, UMA, and NUMA systems. It discusses cache coherence protocols and issues like false sharing. It also covers scheduling and synchronization challenges in multiprocessor systems like load balancing, task assignment, and avoiding priority inversions.

1. Multiprocessor/Multicore Systems Scheduling, Synchronization

2. Multiprocessors Definition: A computer system in which two or more CPUs share full access to a common RAM

3. Multiprocessor/Multicore Hardware (ex.1) Bus-based multiprocessors

4. Multiprocessor/Multicore Hardware (ex.2) UMA (uniform memory access) Not/hardly scalable Bus-based architectures -> saturation Crossbars too expensive (wiring constraints) Possible solutions Reduce network traffic by caching Clustering -> non-uniform memory latency behaviour (NUMA.

5. Multiprocessor/Multicore Hardware (ex.3) NUMA (non-uniform memory access) Single address space visible to all CPUs Access to remote memory slower than to local Cache-controller/MMU determines whether a reference is local or remote When caching is involved, it's called CC-NUMA (cache coherent NUMA) Typically Read Replication (write invalidation)

6. Cache-coherence

7. Cache coherence (cont) cache coherency protocols are based on a set of (cache block) states and state transitions : 2 types of protocols write-update write-invalidate (suffers from false sharing) Some invalidations are not necessary for correct program execution: Processor 1: Processor 2: while (true) do while (true) do A = A + 1 B = B + 1 If A and B are located in the same cache block, a cache miss occurs in each loop-iteration due to a ping-pong of invalidations

8. On multicores Reason for multicores : physical limitations can cause significant heat dissipation and data synchronization problems In addition to operating system (OS) support, adjustments to existing software are required to maximize utilization of the computing resources provided by multi-core processors. Virtual machine approach again in focus . Intel Core 2 dual core processor, with CPU-local Level 1 caches+ shared, on-die Level 2 cache.

9. On multicores (cont) Also possible (figure from www.microsoft.com/licensing/highlights/multicore.mspx)

10. OS Design issues (1): Who executes the OS/scheduler(s)? Master/slave architecture: Key kernel functions always run on a particular processor Master is responsible for scheduling; slave sends service request to the master Disadvantages Failure of master brings down whole system Master can become a performance bottleneck Peer architecture: Operating system can execute on any processor Each processor does self-scheduling New issues for the operating system Make sure two processors do not choose the same process

11. Master-Slave multiprocessor OS Bus

12. Non-symmetric Peer Multiprocessor OS Each CPU has its own operating system Bus

13. Symmetric Peer Multiprocessor OS Symmetric Multiprocessors SMP multiprocessor model Bus

14. Scheduling in Multiprocessors Recall: Tightly coupled multiprocessing ( SMPs ) Processors share main memory Controlled by operating system Different degrees of parallelism Independent and Coarse-Grained Parallelism no or very limited synchronization can by supported on a multiprocessor with little change (and a bit of salt  ) Medium-Grained Parallelism collection of threads; usually interact frequently Fine-Grained Parallelism Highly parallel applications; specialized and fragmented area

15. Design issues 2: Assignment of Processes to Processors Per-processor ready-queues vs global ready-queue Permanently assign process to a processor; Less overhead A processor could be idle while another processor has a backlog Have a global ready queue and s chedule to any available processor can become a bottleneck Task migration not cheap

16. Multiprocessor Scheduling: per partition RQ Space sharing multiple threads at same time across multiple CPUs

17. Multiprocessor Scheduling: Load sharing / Global ready queue Timesharing note use of single data structure for scheduling

18. Multiprocessor Scheduling Load Sharing: a problem Problem with communication between two threads both belong to process A both running out of phase

19. Design issues 3: Multiprogramming on processors? Experience shows: Threads running on separate processors (to the extend of dedicating a processor to a thread) yields dramatic gains in performance Allocating processors to threads ~ allocating pages to processes (can use working set model?) Specific scheduling discipline is less important with more than on processor; the decision of “distributing” tasks is more important

20. Gang Scheduling Approach to address the prev. problem : Groups of related threads scheduled as a unit (a gang) All members of gang run simultaneously on different timeshared CPUs All gang members start and end time slices together

21. Gang Scheduling: another option

22. Multiprocessor Thread Scheduling Dynamic Scheduling Number of threads in a process are altered dynamically by the application Programs (through thread libraries) give info to OS to manage parallelism OS adjusts the load to improve use Or os gives info to run-time system about available processors, to adjust # of threads. i.e dynamic vesion of partitioning:

23. Summary: Multiprocessor Thread Scheduling Load sharing : processors/threads not assigned to particular processors load is distributed evenly across the processors; needs c entral queue ; may be a bottleneck preemptive threads are unlikely to resume execution on the same processor; c ache use is less efficient Gang scheduling : Assigns threads to particular processors (simultaneous scheduling of threads that make up a process) Useful where performance severely degrades when any part of the application is not running (due to synchronization) Extreme version: Dedicated processor assignment (no multiprogramming of processors)

24. Multiprocessor Scheduling and Synchronization Priorities + blocking synchronization may result in: priority inversion : low-priority process P holds a lock, high-priority process waits, medium priority processes do not allow P to complete and release the lock fast (scheduling less efficient). To cope/avoid this: use priority inheritance use non-blocking synchronization (wait-free, lock-free, optimistic synchronization) convoy effect : processes need a resource for short time, the process holding it may block them for long time (hence, poor utilization) non-blocking synchronization is good here, too

25. Readers-Writers non-blocking synchronization (some slides are adapted from J. Anderson’s slides on same topic)

26. The Mutual Exclusion Problem Locking Synchronization N processes, each with this structure: while true do Noncritical Section; Entry Section; Critical Section; Exit Section od Basic Requirements: Exclusion: Invariant(# in CS  1). Starvation-freedom: (process i in Entry) leads-to (process i in CS). Can implement by “busy waiting” ( spin locks ) or using kernel calls .

27. Non-blocking Synchronization The problem: Implement a shared object without mutual exclusion . Shared Object: A data structure ( e.g ., queue) shared by concurrent processes. Why? To avoid performance problems that result when a lock-holding task is delayed . To avoid priority inversions (more on this later). Locking

28. Non-blocking Synchronization Two variants: Lock-free: Only system-wide progress is guaranteed. Usually implemented using “retry loops.” Wait-free: Individual progress is guaranteed. Code for object invocations is purely sequential.

29. Readers/Writers Problem [Courtois, et al. 1971.] Similar to mutual exclusion, but several readers can execute critical section at once . If a writer is in its critical section, then no other process can be in its critical section . + no starvation, fairness

30. Solution 1 Readers have “priority”… Reader:: P( mutex ); rc := rc + 1; if rc = 1 then P( w ) fi; V( mutex ); CS; P( mutex ); rc := rc  1; if rc = 0 then V( w ) fi; V( mutex ) Writer:: P( w ); CS; V( w ) “ First” reader executes P(w). “Last” one executes V(w).

31. Solution 2 Writers have “priority” … readers should not build long queue on r, so that writers can overtake => mutex3 Reader:: P( mutex3 ); P( r ); P( mutex1 ); rc := rc + 1; if rc = 1 then P( w ) fi; V( mutex1 ); V( r ); V( mutex3 ); CS; P( mutex1 ); rc := rc  1; if rc = 0 then V( w ) fi; V( mutex1 ) Writer:: P( mutex2 ); wc := wc + 1; if wc = 1 then P( r ) fi; V( mutex2 ); P( w ); CS; V( w ); P( mutex2 ); wc := wc  1; if wc = 0 then V( r ) fi; V( mutex2 )

32. Properties If several writers try to enter their critical sections, one will execute P( r ), blocking readers. Works assuming V( r ) has the effect of picking a process waiting to execute P( r ) to proceed. Due to mutex3 , if a reader executes V( r ) and a writer is at P( r ), then the writer is picked to proceed.

33. Concurrent Reading and Writing [Lamport ‘77] Previous solutions to the readers/writers problem use some form of mutual exclusion . Lamport considers solutions in which readers and writers access a shared object concurrently . Motivation: Don’t want writers to wait for readers. Readers/writers solution may be needed to implement mutual exclusion (circularity problem).

34. Interesting Factoids This is the first ever lock-free algorithm: guarantees consistency without locks An algorithm very similar to this is implemented within an embedded controller in Mercedes automobiles!!

35. The Problem Let v be a data item, consisting of one or more digits. For example, v = 256 consists of three digits, “2”, “5”, and “6”. Underlying model: Digits can be read and written atomically. Objective: Simulate atomic reads and writes of the data item v .

36. Preliminaries Definition: v [ i ] , where i  0, denotes the i th value written to v. (v [0] is v ’s initial value.) Note: No concurrent writing of v . Partitioning of v : v 1  v m . v i may consist of multiple digits . To read v : Read each v i (in some order). To write v : Write each v i (in some order).

37. More Preliminaries We say: r reads v [ k,l ] . Value is consistent if k = l . write: k write: k + i write: l        read v 3 read v 2 read v m -1 read v 1 read v m read r: 

38. Theorem 1 If v is always written from right to left, then a read from left to right obtains a value v 1 [ k 1 , l 1 ] v 2 [ k 2 , l 2 ] … v m [ k m , l m ] where k 1  l 1  k 2  l 2  …  k m  l m . Example: v = v 1 v 2 v 3 = d 1 d 2 d 3 Read reads v 1 [0,0] v 2 [1,1] v 3 [2,2] . read :  read v 1 read d 1  read v 2 read d 2  read v 3 read d 3 write:1    w v 3 w v 2 w v 1 w d 3 w d 2 w d 1 write:0    w v 3 w v 2 w v 1 w d 3 w d 2 w d 1 write:2    w v 3 w v 2 w v 1 w d 3 w d 2 w d 1

39. Another Example read : write:0    w v 2 w v 1 w d 3 w d 4 w d 1  w d 2 write:1    w v 2 w v 1 w d 3 w d 4 w d 1  w d 2  read v 1 r d 1  r d 2  read v 2 r d 4  r d 3 v = v 1 v 2 d 1 d 2 d 3 d 4 Read reads v 1 [0,1] v 2 [1,2] . write:2    w v 2 w v 1 w d 3 w d 4 w d 1  w d 2

40. Theorem 2 Assume that i  j implies that v [ i ]  v [ j ] , where v = d 1 … d m . (a) If v is always written from right to left, then a read from left to right obtains a value v [ k , l ]  v [ l ] . (b) If v is always written from left to right, then a read from right to left obtains a value v [ k , l ]  v [ k ] .

41. Example of (a) v = d 1 d 2 d 3 Read obtains v [0,2] = 390 < 400 = v [2] . read :  read d 1  read d 2  read d 3 write:1(399)    w d 3 w d 2 w d 1 9 9 3 write:0(398)    w d 3 w d 2 w d 1 8 9 3 write:2(400)    w d 3 w d 2 w d 1 0 0 4

42. Example of (b) v = d 1 d 2 d 3 Read obtains v [0,2] = 498 > 398 = v [0] . read :  read d 3  read d 2  read d 1 write:1(399)    w d 1 w d 2 w d 3 3 9 9 write:0(398)    w d 1 w d 2 w d 3 3 9 8 write:2(400)    w d 1 w d 2 w d 3 4 0 0

43. Readers/Writers Solution :> means assign larger value.  V1 means “left to right”.  V2 means “right to left”. Writer::  V1 :> V1; write D;  V2 := V1 Reader::  repeat temp := V2 read D  until V1 = temp

44. Proof Obligation Assume reader reads V2 [ k 1 , l 1 ] D [ k 2 , l 2 ] V1 [ k 3 , l 3 ] . Proof Obligation: V2 [ k 1 , l 1 ] = V1 [ k 3 , l 3 ]  k 2 = l 2 .

45. Proof By Theorem 2, V2 [ k 1 , l 1 ]  V2 [ l 1 ] and V1 [ k 3 ]  V1 [ k 3 , l 3 ] . (1) Applying Theorem 1 to V2 D V1, k 1  l 1  k 2  l 2  k 3  l 3 . (2) By the writer program, l 1  k 3  V2 [ l 1 ]  V1 [ k 3 ] . (3) (1), (2), and (3) imply V2 [ k 1 , l 1 ]  V2 [ l 1 ]  V1 [ k 3 ]  V1 [ k 3 , l 3 ] . Hence, V2 [ k 1 , l 1 ] = V1 [ k 3 , l 3 ]  V2 [ l 1 ] = V1 [ k 3 ]  l 1 = k 3 , by the writer’s program.  k 2 = l 2 by (2).

46. Supplemental Reading check: G.L. Peterson, “Concurrent Reading While Writing”, ACM TOPLAS, Vol. 5, No. 1, 1983, pp. 46-55. Solves the same problem in a wait-free manner: guarantees consistency without locks and the unbounded reader loop is eliminated. First paper on wait-free synchronization. Now, very rich literature on the topic. Check also: PhD thesis A. Gidenstam, 2006, CTH PhD Thesis H. Sundell, 2005, CTH

47. Useful Synchronization Primitives Usually Necessary in Nonblocking Algorithms CAS2 extends this CAS(var, old, new)  if var  old then return false fi; var := new; return true  LL(var)  establish “link” to var; return var  SC(var, val)  if “link” to var still exists then break all current links of all processes; var := val; return true else return false fi 

48. Another Lock-free Example Shared Queue type Qtype = record v: valtype; next: pointer to Qtype end shared var Tail: pointer to Qtype; local var old, new: pointer to Qtype procedure Enqueue (input: valtype) new := (input, NIL); repeat old := Tail until CAS2(Tail, old->next, old, NIL, new, new) Tail old Tail old new new retry loop

49. Using Locks in Real-time Systems The Priority Inversion Problem Uncontrolled use of locks in RT systems can result in unbounded blocking due to priority inversions . Time Low Med High t t t 0 1 2 Shared Object Access Priority Inversion Computation not involving object accesses Solution: Limit priority inversions by modifying task priorities . Time Low Med High t 0 t 1 t 2

50. Dealing with Priority Inversions Common Approach: Use lock-based schemes that bound their duration (as shown). Examples: Priority-inheritance and -ceiling protocols. Disadvantages: Kernel support, very inefficient on multiprocessors. Alternative: Use non-blocking objects. No priority inversions or kernel support. Wait-free algorithms are clearly applicable here. What about lock-free algorithms? Advantage: Usually simpler than wait-free algorithms. Disadvantage: Access times are potentially unbounded . But for periodic task sets access times are also predictable!! (check further-reading-pointers)