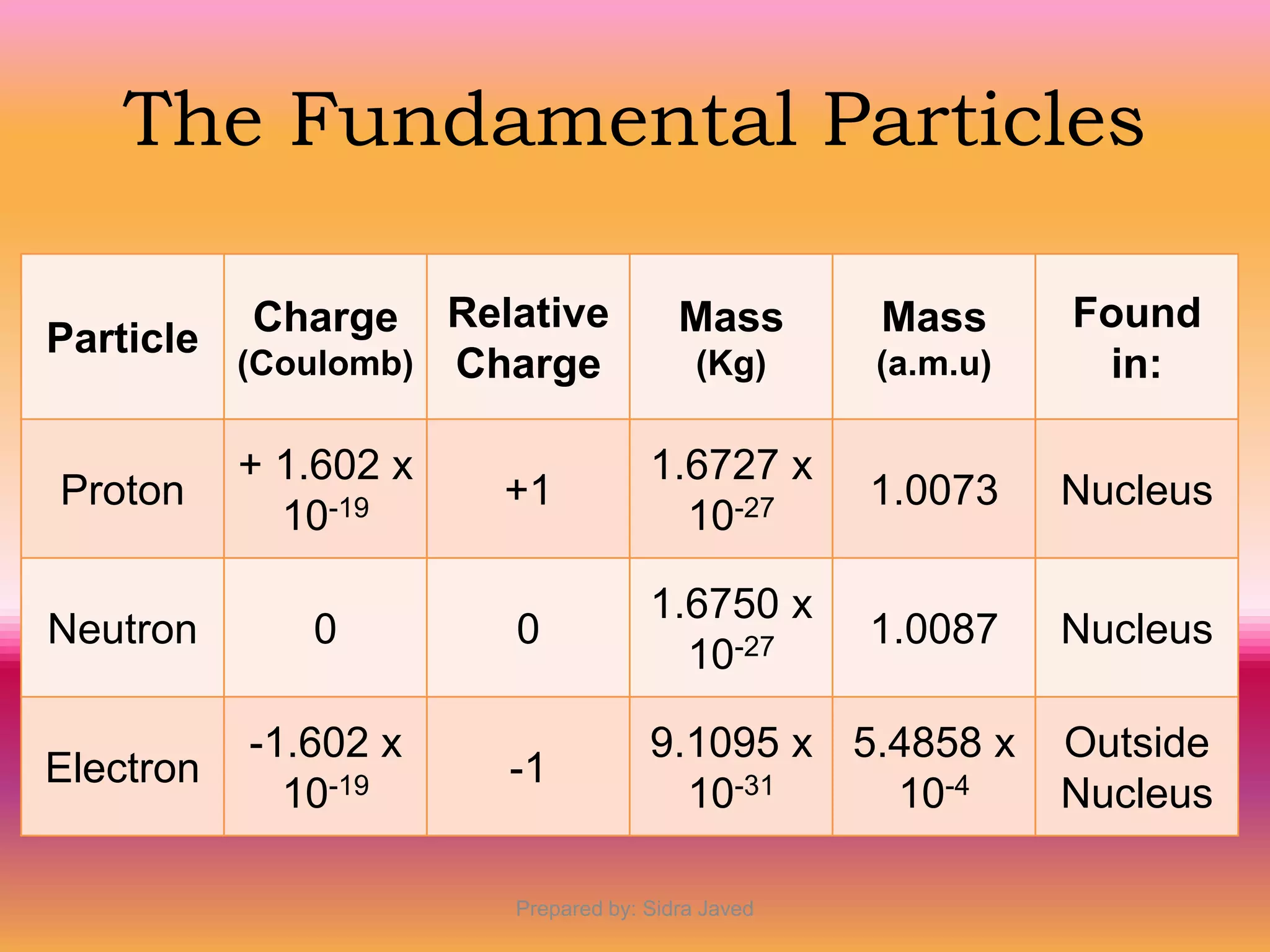
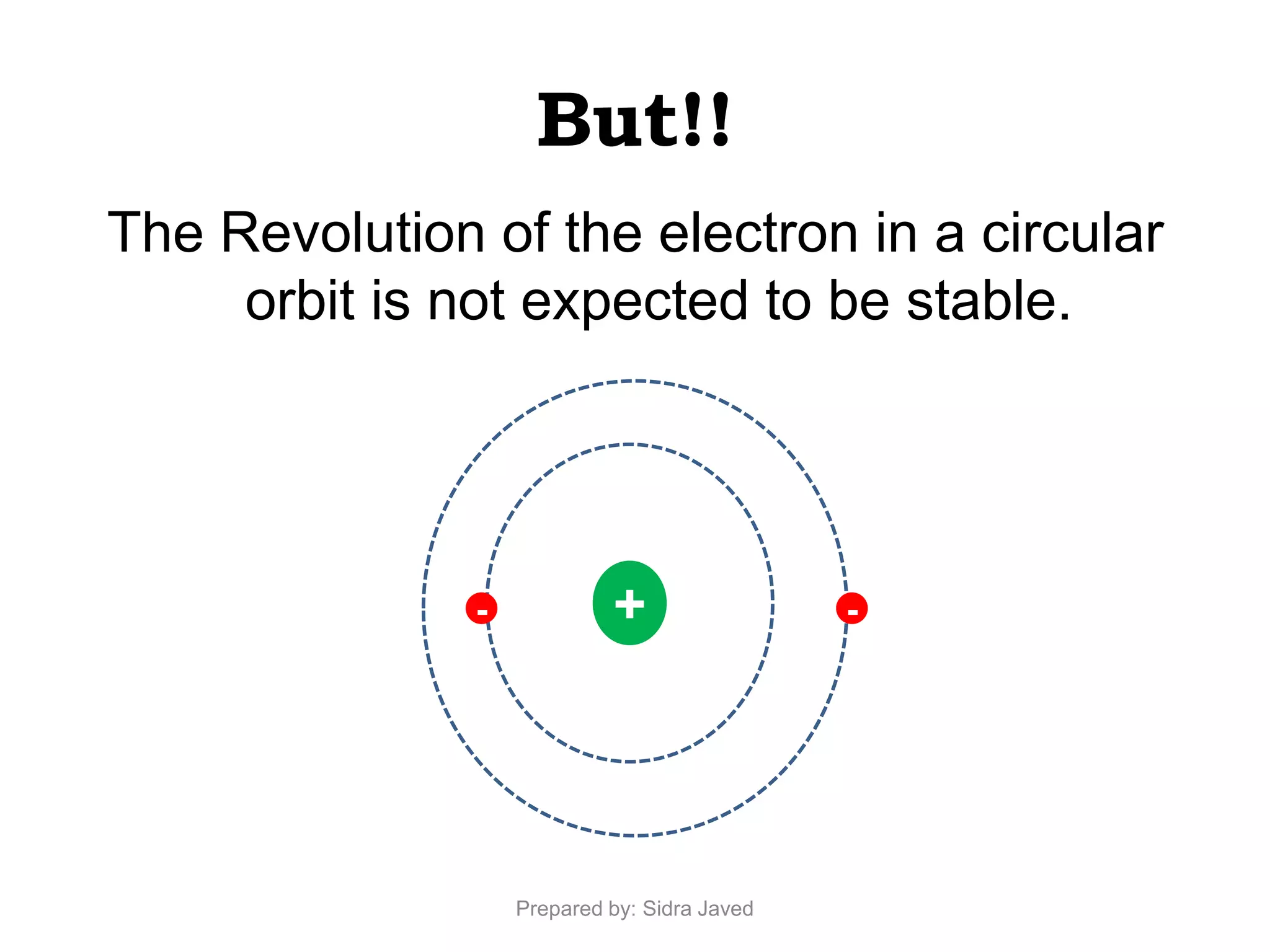
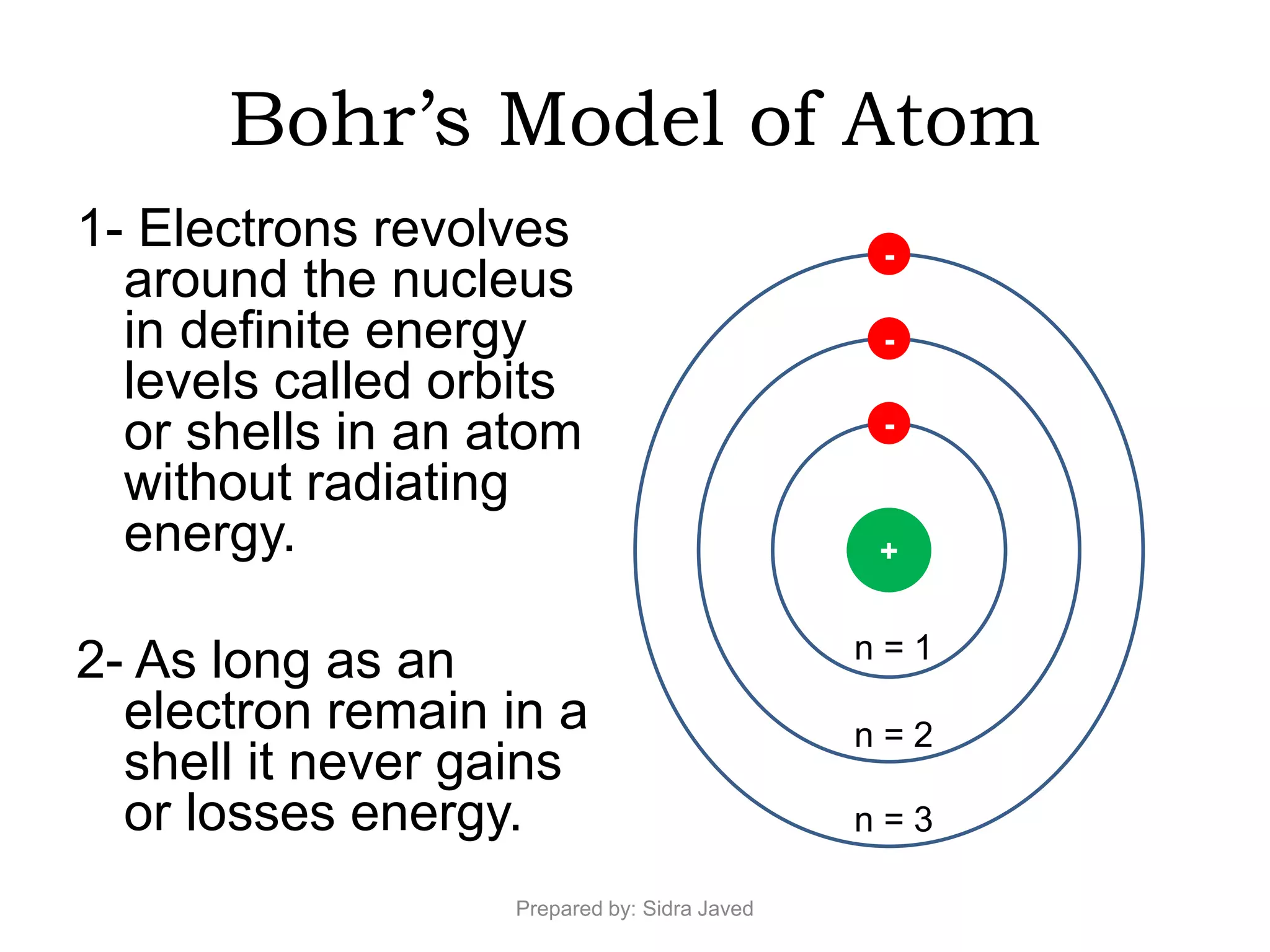
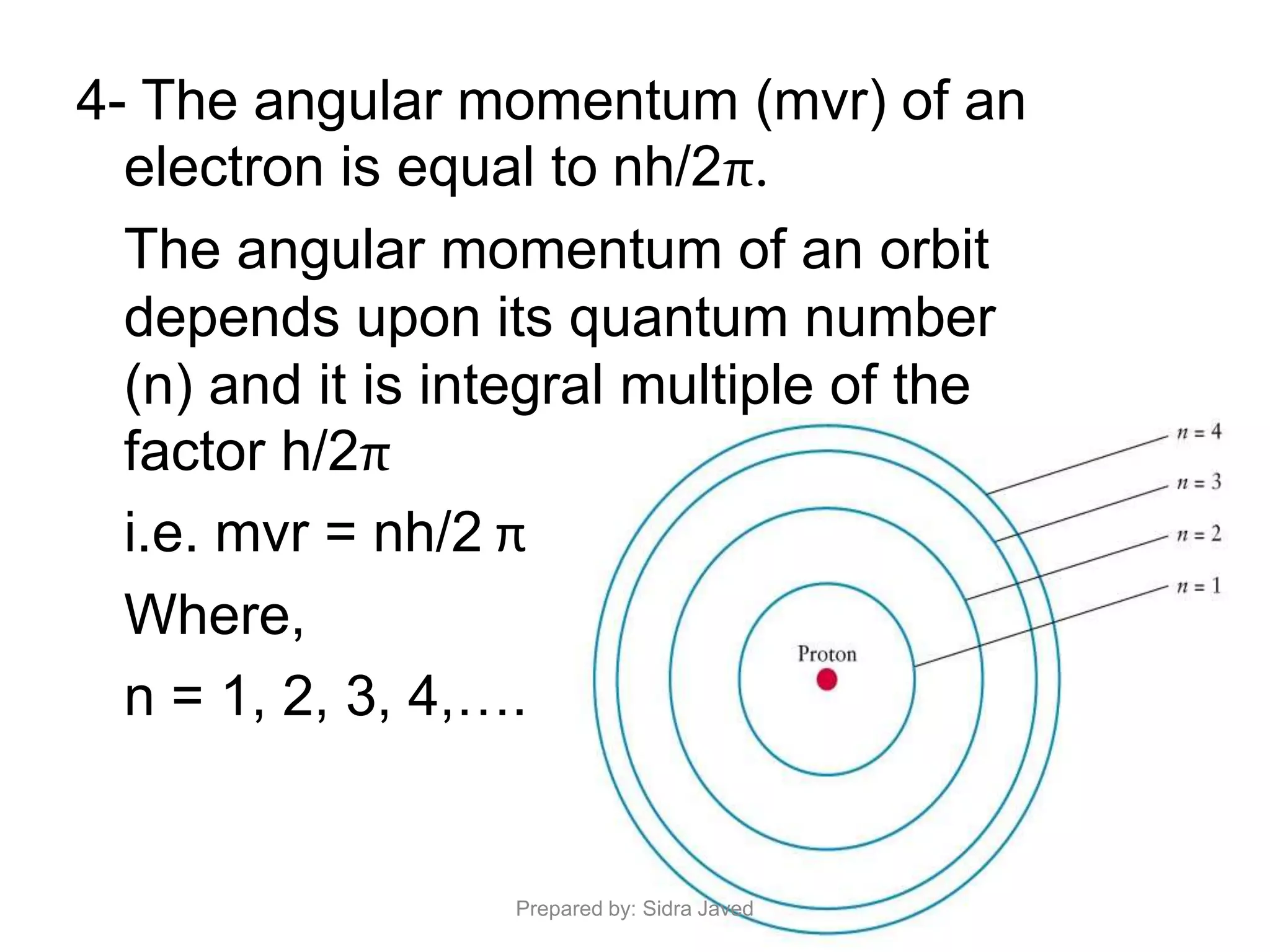
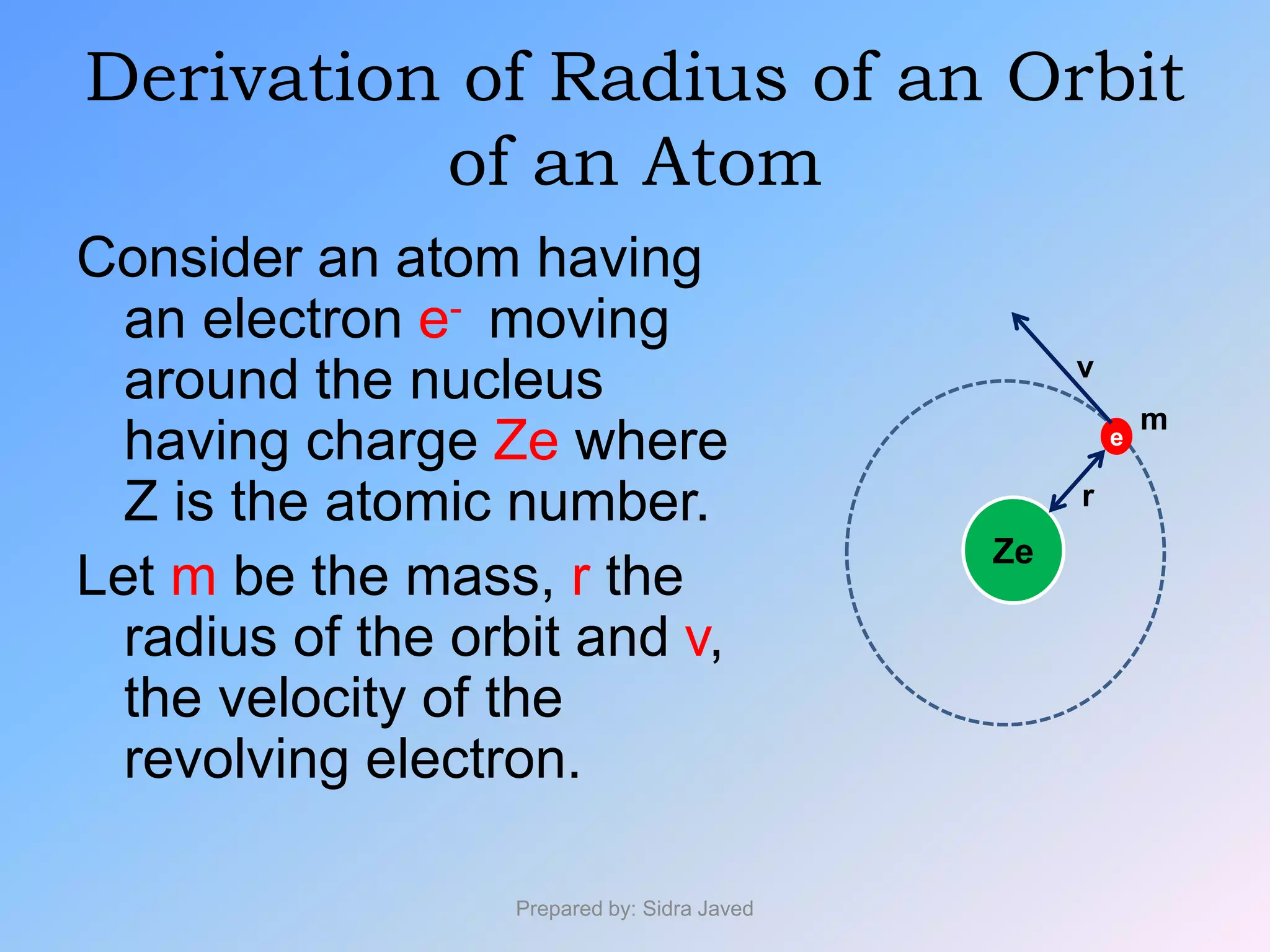
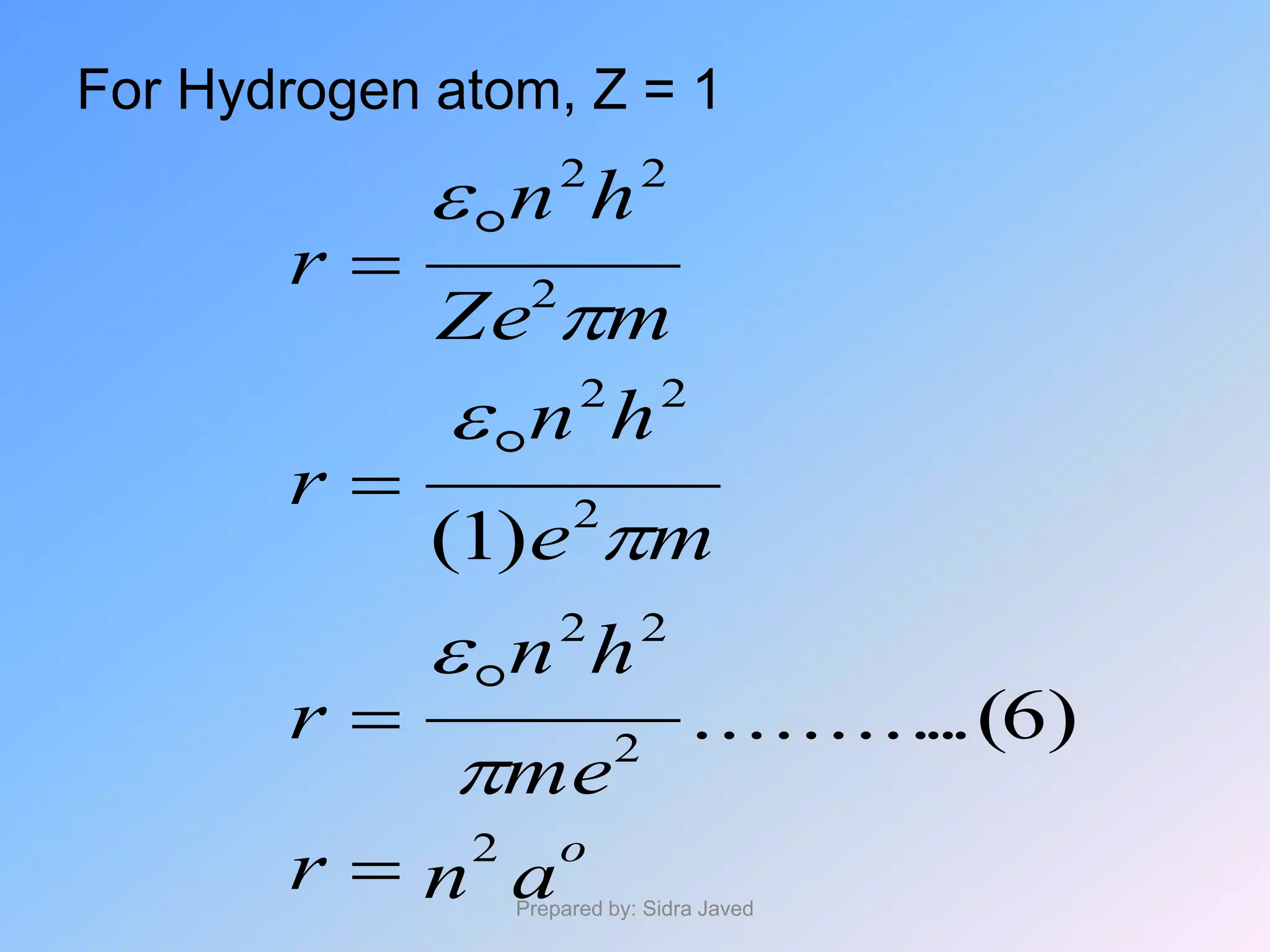1) Bohr's atomic model successfully explained the hydrogen spectrum by postulating that electrons revolve in definite orbits called energy levels without radiating energy.
2) The radius, energy, and frequency of radiation emitted by electrons in different orbits were derived based on Bohr's model.
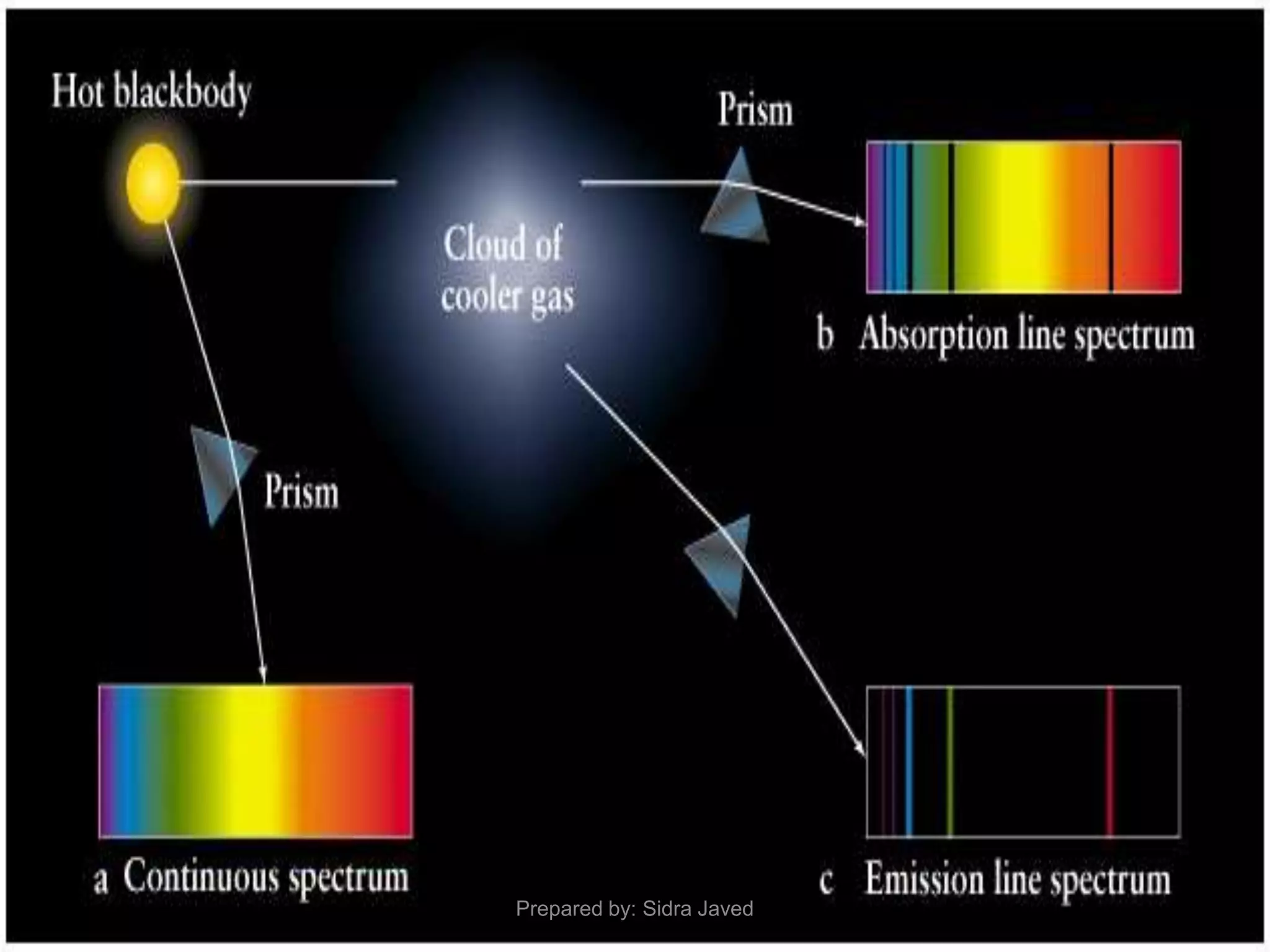
3) Bohr's model showed that electrons can jump between discrete energy levels, emitting or absorbing photons of specific frequencies corresponding to the energy differences between levels.