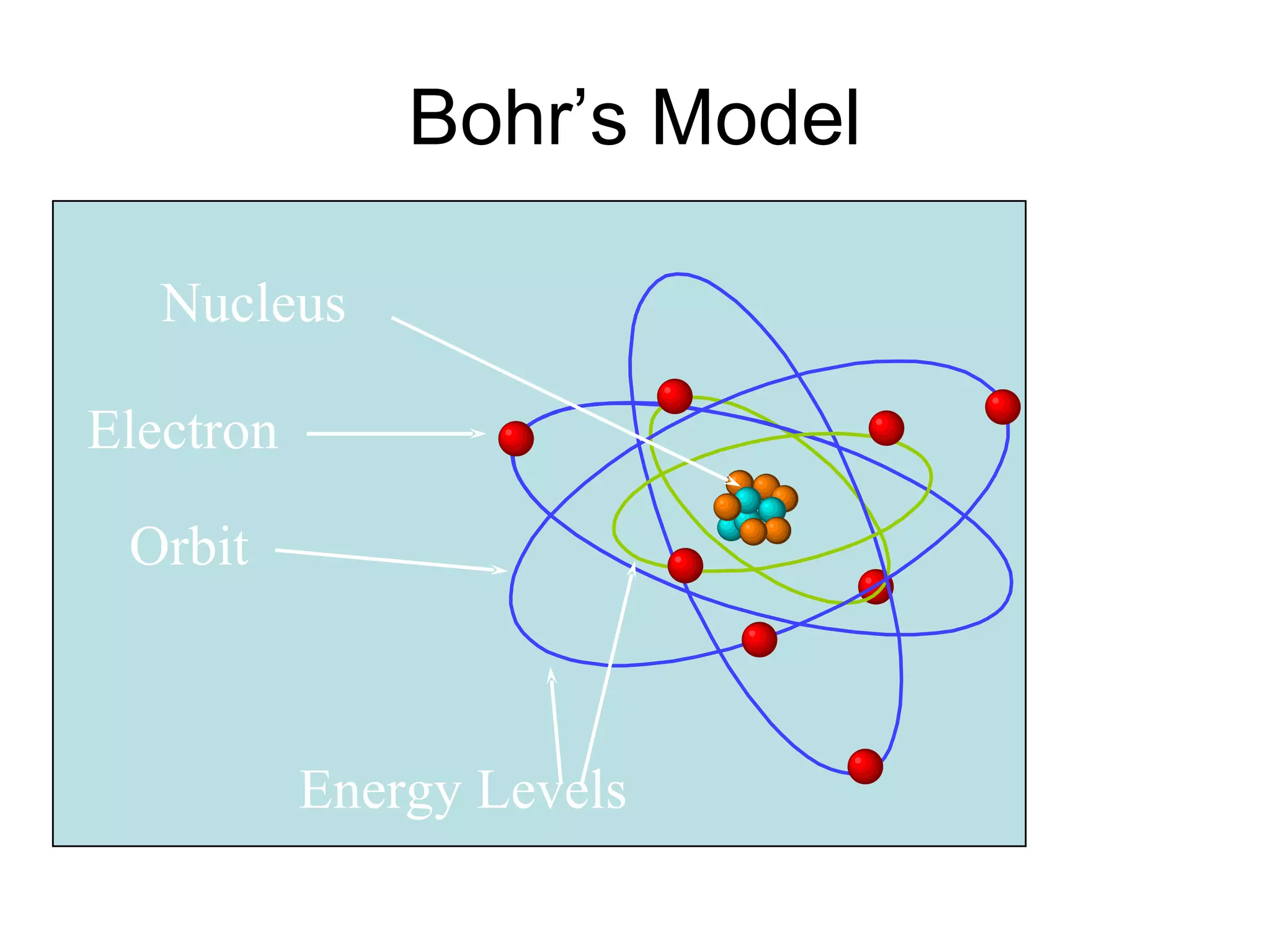
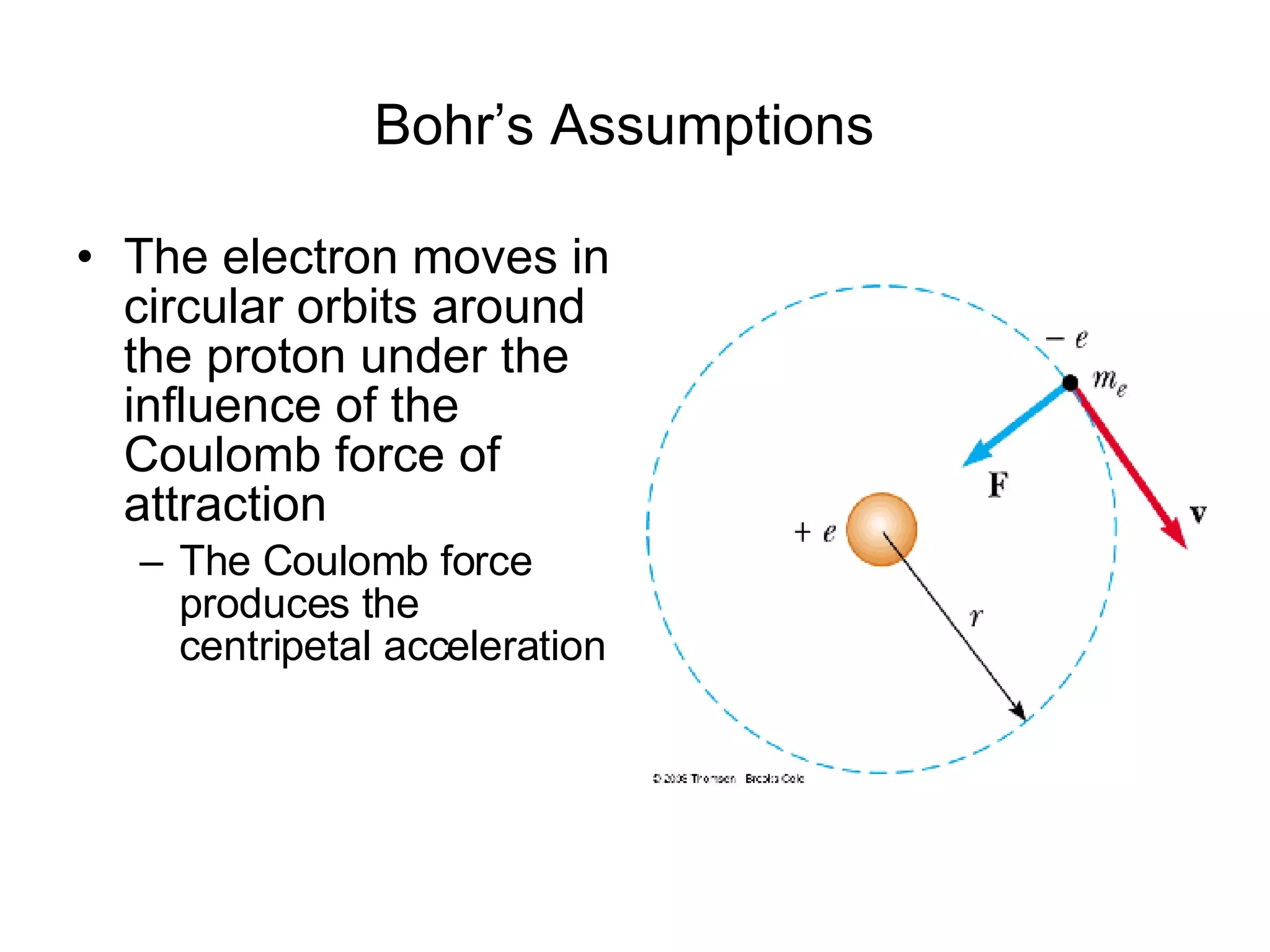
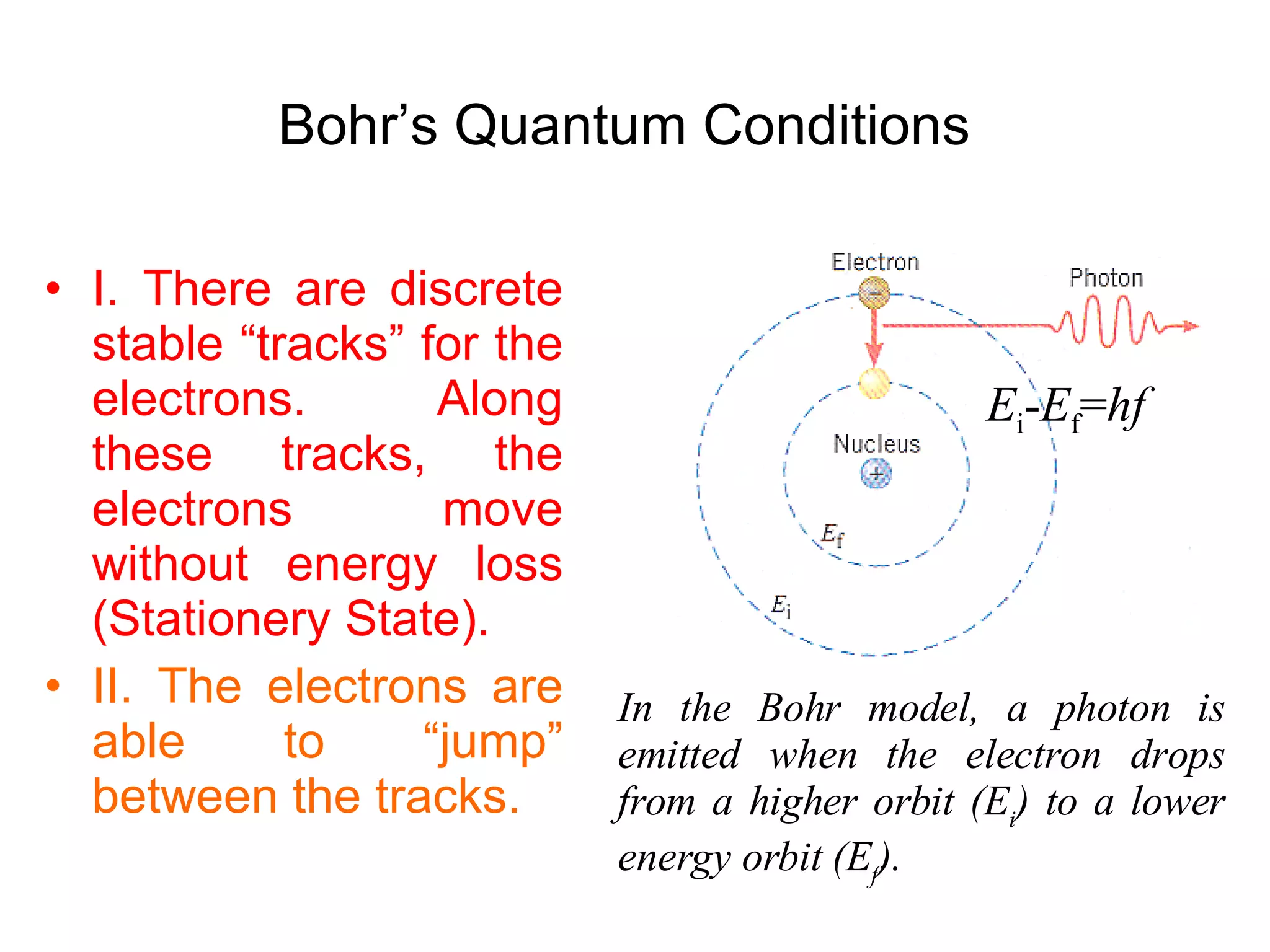
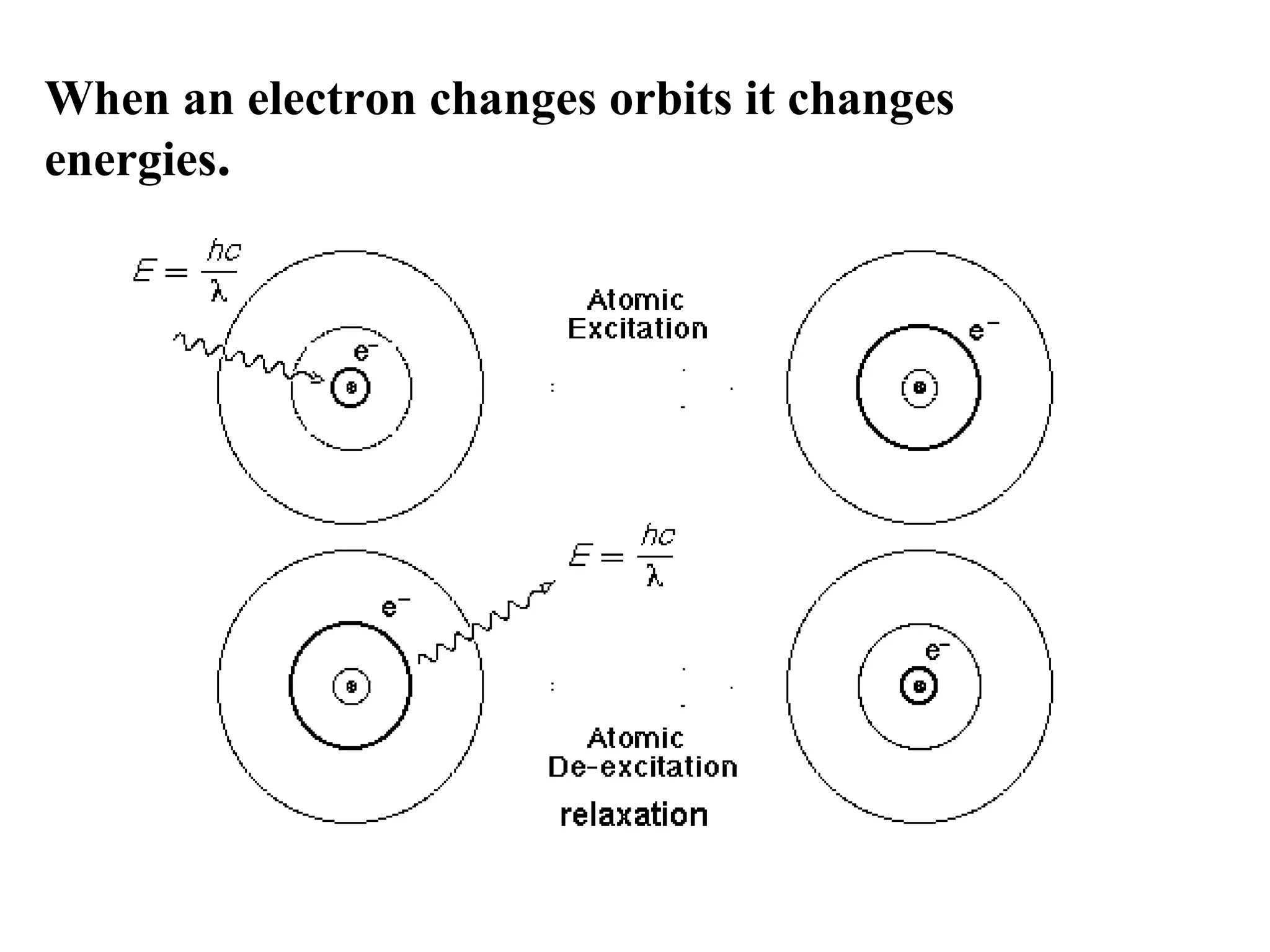
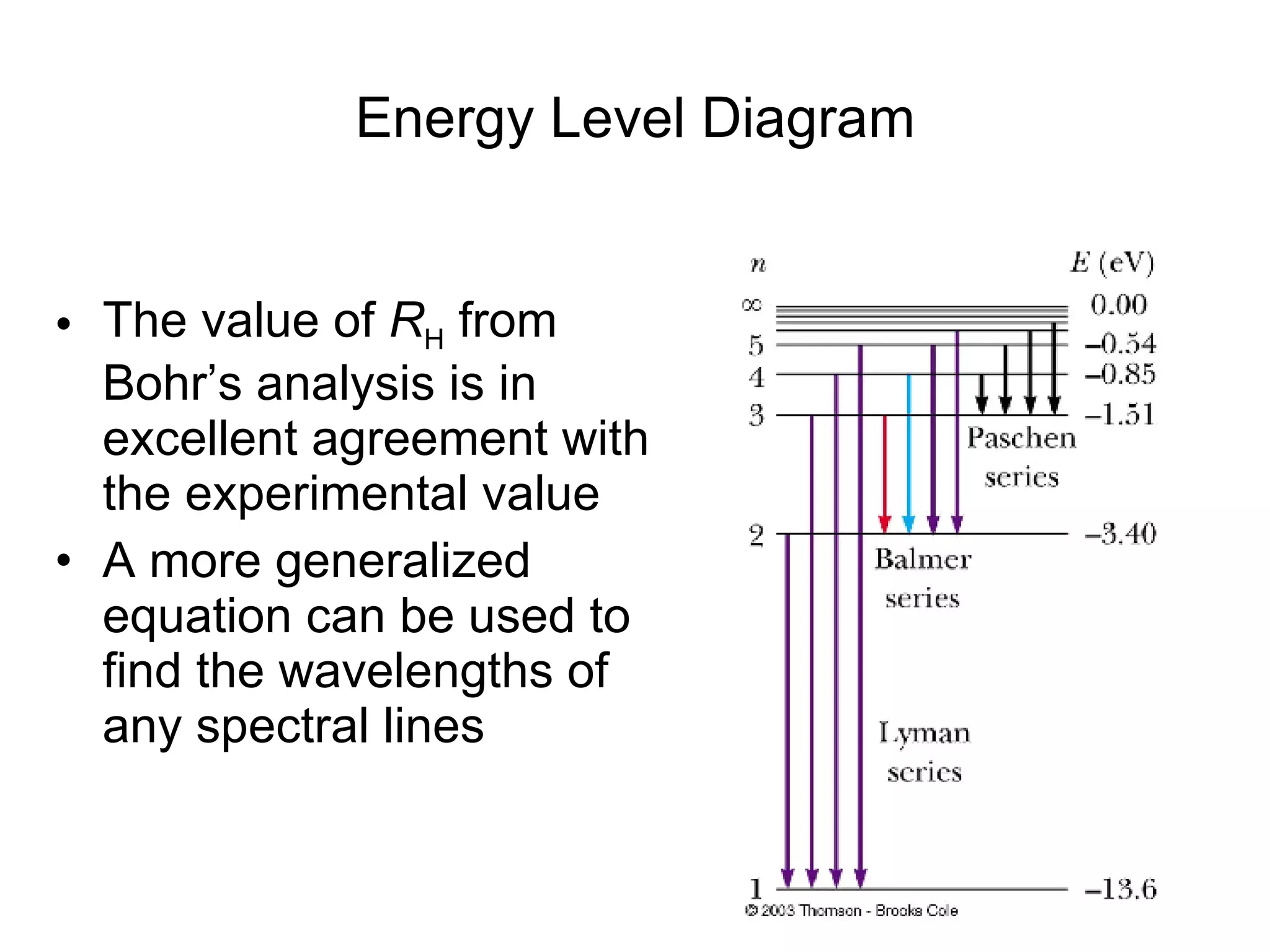
The document summarizes Niels Bohr's model of the atom from 1913. Bohr proposed that electrons orbit the nucleus in discrete, quantized energy levels. Electrons can jump between these energy levels, absorbing or emitting photons of light. The energy of the photons depends on the energy difference between the initial and final orbit. Bohr's model could only explain the hydrogen atom and failed to account for effects like the Zeeman and Stark effects seen in other atoms. Later developments in quantum mechanics disproved Bohr's idea of electrons having definite orbits.

1. Bohr’s Model Nucleus Electron Orbit Energy Levels Nucleus Electron Orbit Energy Levels

2. The Bohr Model In 1913 Bohr provided an explanation of atomic spectra His model includes both classical and non-classical ideas His model included an attempt to explain why the atom was stable

3. Bohr said classical view is wrong. Need a new theory — now called QUANTUM or WAVE MECHANICS . Bohr Model

4. Bohr’s Assumptions The electron moves in circular orbits around the proton under the influence of the Coulomb force of attraction The Coulomb force produces the centripetal acceleration

5. Bohr’s Quantum Conditions I. There are discrete stable “tracks” for the electrons. Along these tracks, the electrons move without energy loss (Stationery State). II. The electrons are able to “jump” between the tracks. In the Bohr model, a photon is emitted when the electron drops from a higher orbit (E i ) to a lower energy orbit (E f ). E i - E f = hf

6. Bohr Model: Orbit Radius Bohr assumed that the angular momentum of the electron was quantized and could have only discrete values that were integral multiples of h /2  , where h is Plank’s constant m e vr = nh /(2  ); n =1, 2, 3,… v = nh /(2  m e r )

7. Bohr Model: Energy of electron in orbit In each orbit, the energy of the electron is restricted to a certain value - E = - R H /n 2 R H is a constant in energy units: = 2.179 X 10 -18 J/atom = 13.6eV/atom = 1312 KJ/mole Number of orbit = n = 1, 2, 3, etc.

8. When an electron changes orbits it changes energies .

9. Energy is emitted in the form of light (electromagnetic radiation as the electron moves from a higher orbit to a lower one (from a higher energy level to a lower one). Energy is absorbed as electricity or heat as the electron moves from a lower to a higher orbit (energy level).

10. Specific Energy Levels The lowest energy state is called the ground state This corresponds to n = 1 Energy is –13.6 eV The next energy level has an energy of –3.40 eV The energies can be compiled in an energy level diagram The ionization energy is the energy needed to completely remove the electron from the atom The ionization energy for hydrogen is 13.6 eV

11. Energy Level Diagram The value of R H from Bohr’s analysis is in excellent agreement with the experimental value A more generalized equation can be used to find the wavelengths of any spectral lines

12. Orbit Radii and Energies r n =0.0529  n 2 (nm) E n =-13.6/ n 2 (eV) Energy difference between the levels  E =13.6(1/ n f 2 -1/ n i 2 ) For example, between n =1 and n =2 (as drawn in the picture)  E =13.6(1/ n f 2 -1/ n i 2 )=13.6(1/1 2 -1/2 2 )=10.2 eV  E= 10.2 eV Final state, n f Initial State, n i

13. PROBLEMS WITH THE BOHR ATOM A) It is only successful with the Hydrogen atom B) It could not account for extra lines in the H emission spectrum when a magnetic field was applied to the gas: Zeeman Effect : Splitting of Spectral lines under the external magnetic fields Stark Effect : Splitting of Spectral lines under the external electric field

14. C) PARTICLE-WAVE DUALISM 1923-24 - The French physicist de Broglie says that if light waves exhibit particle properties, under certain circumstances, then particles of matter should show wave characteristics under certain circumstances. h = 6.63 X 10-34 kg m2/sec if m is large and the speed is small, then  is so small as to be meaningless- 10 -34 m.

15. D) The idea of circular orbits and knowing where the electron is located is impossible: In 1927 Werner Heisenberg showed from quantum mechanics that it is impossible to know simultaneously, with absolute precision, both the position and the momentum of a particle such as an electron. The Heisenberg Uncertainty Principle! ▲ x * m ▲ v ≥ h/4 