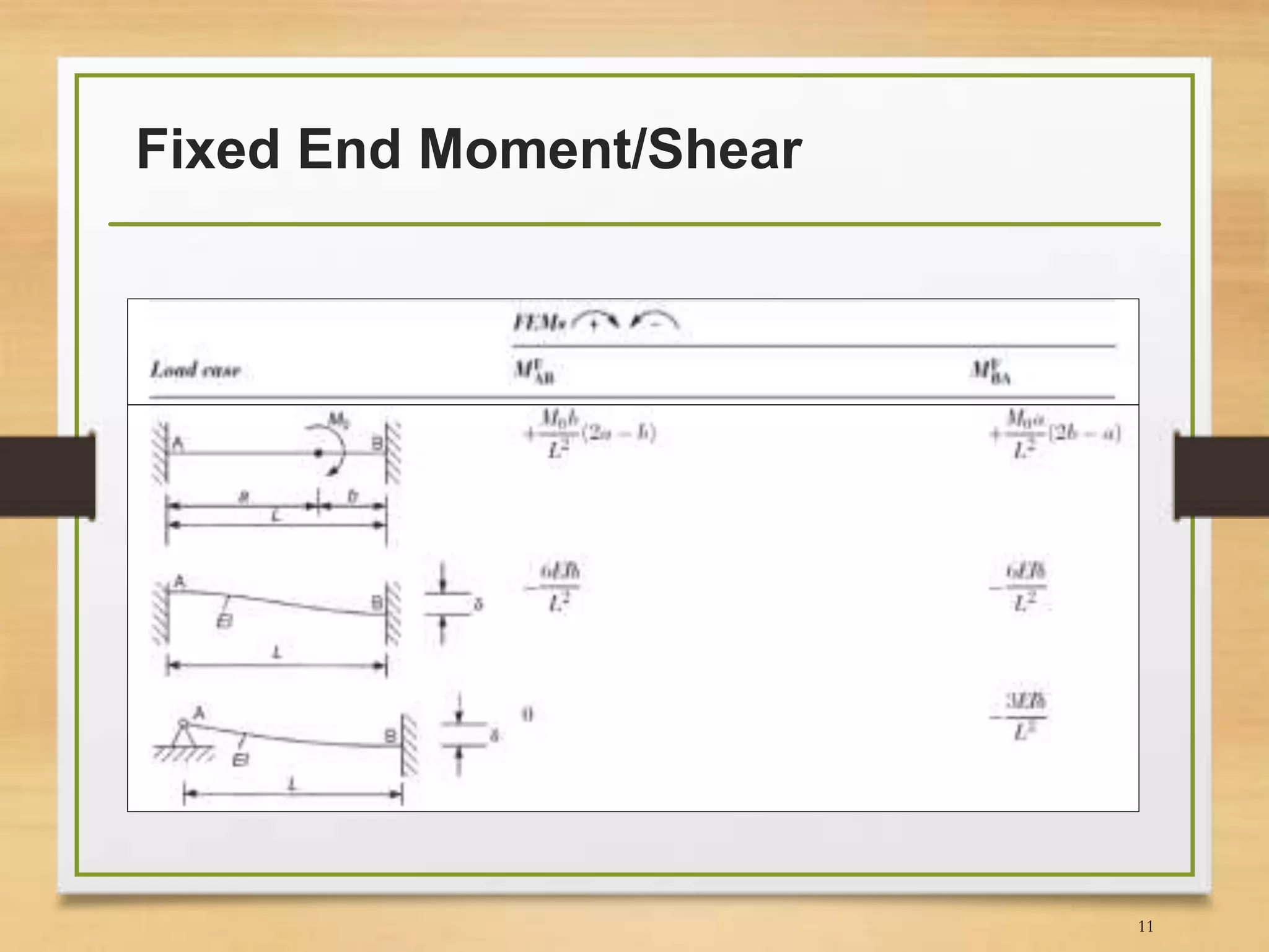
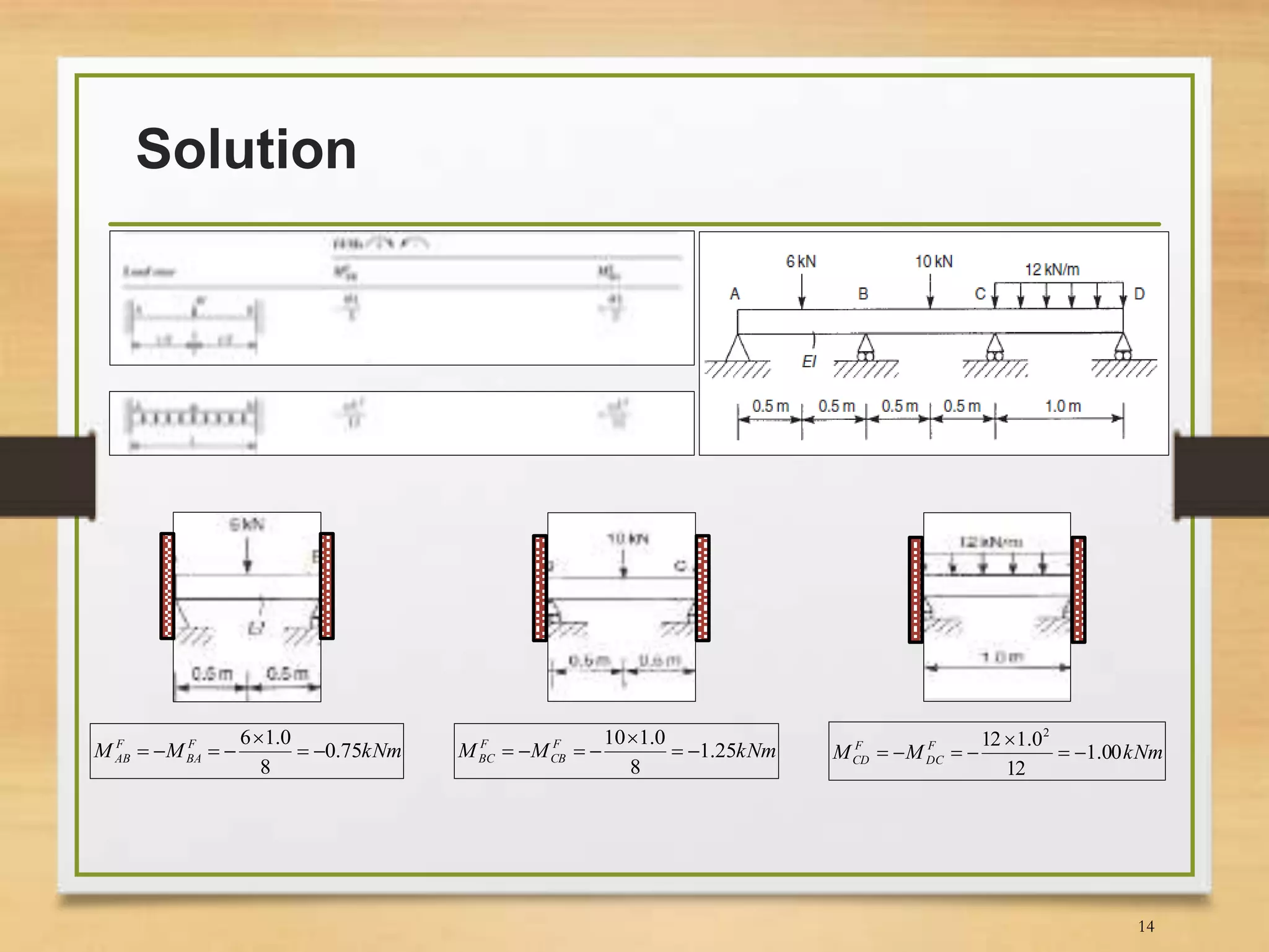
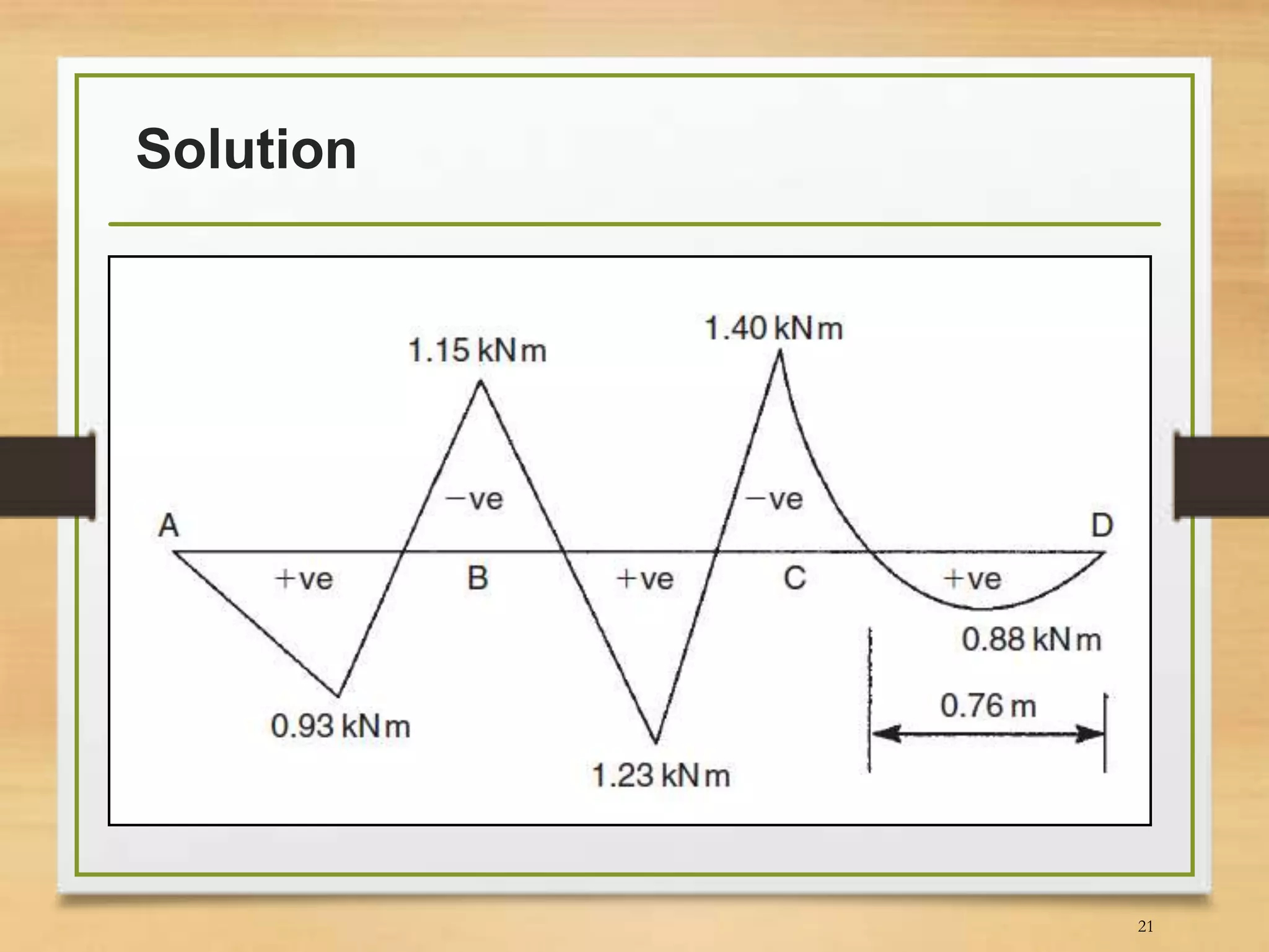
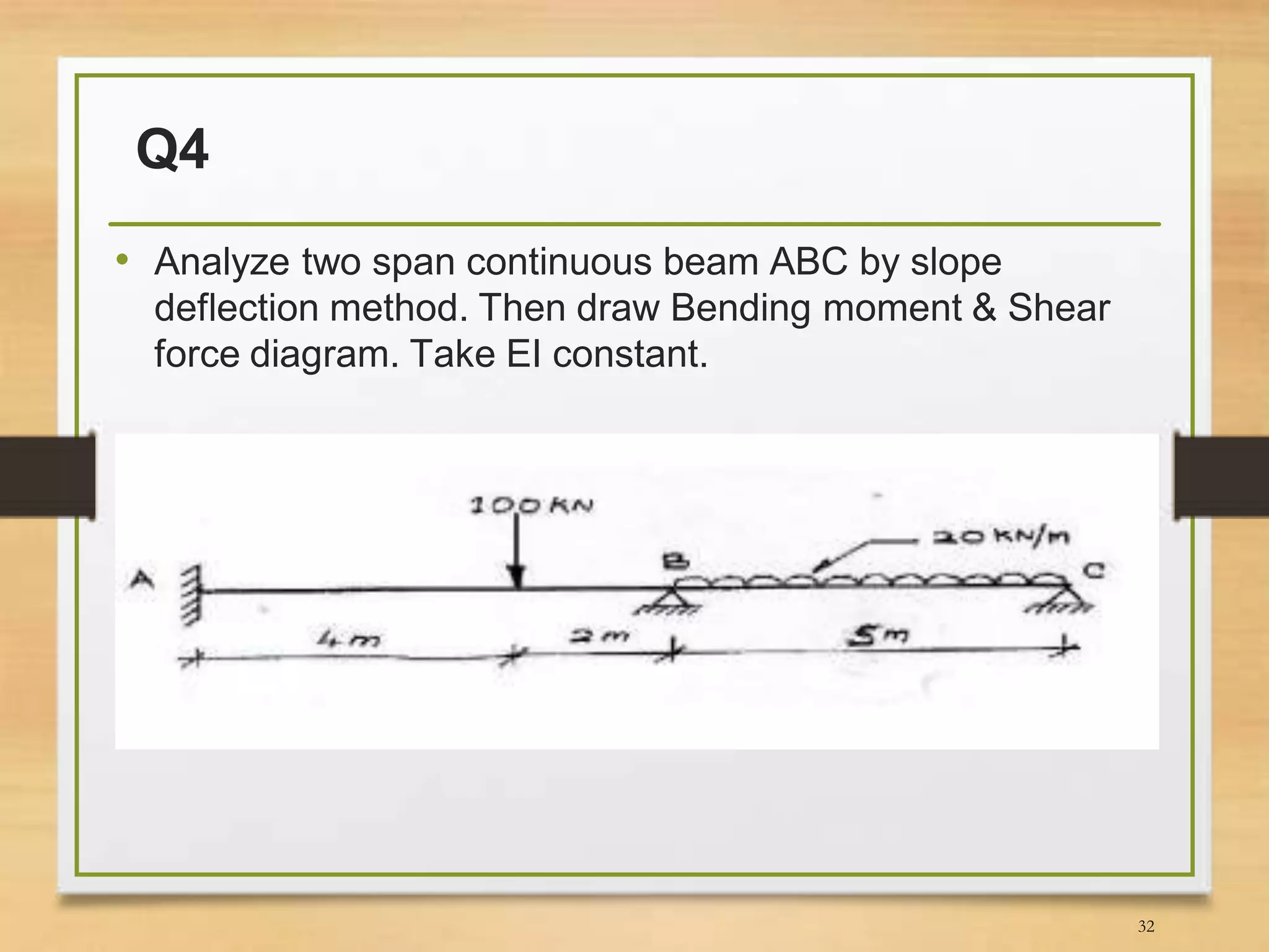
This document discusses the slope-deflection method for analyzing beams and frames. It provides the theory and equations of the slope-deflection method. Examples are included to demonstrate how to use the method to determine support reactions, member end moments, and draw bending moment and shear force diagrams.

1. Structural Design and Inspection-
Deflection and Slope of Beams
By
Dr. Mahdi Damghani
2016-2017
1

2. Suggested Readings
Reference 1
Chapter 16
2

3. Objective
• To obtain slope and deflection of beam and frame
structures using slope-deflection method
3

4. Introduction
• Structural analysis method for beams and frames
introduced in 1914 by George A. Maney
• This method was later replaced by moment
distribution method which is more advanced and
useful (students are encouraged) to study this
separately
4

5. Slope-Deflection Method
• Sign convention:
• Moments, slopes,
displacements,
shear are all in
positive direction as
shown
5
• Axial forces are
ignored
 xSM
dx
vd
EI ABAB2
2









21
32
1
2
62
2
CxC
x
S
x
MEIv
C
x
SxM
dx
dv
EI
ABAB
ABAB

6. Slope-Deflection Method
6
 AA vv
dx
dv
x ,0@  








AAABAB
AABAB
EIvxEI
x
S
x
MEIv
EI
x
SxM
dx
dv
EI


62
2
32
2
 BB vv
dx
dv
Lx ,@  








AAABABB
AABABB
EIvLEI
L
S
L
MEIv
EI
L
SLMEI


62
2
32
2
Solving for MAB and SAB
 



 BABAAB vv
LL
EI
M
3
2
2
  



 BABAAB vv
LL
EI
S
26
2

 



 BABABA vv
LL
EI
M
3
2
2
  



 BABABA vv
LL
EI
S
26
2


7. Slope-Deflection Method
• Last 4 equations obtained in previous slide are called
slope-deflection equations
• They establish force-displacement relationship
• This method can find exact solution to indeterminate
structures
7

8. Slope-Deflection Method
• The beam we considered
so far did not have any
external loading from A to B
8
• In the presence of mid-span loading (common engineering
problems) the equations become:
  F
ABBABAAB Mvv
LL
EI
M 




3
2
2
   F
ABBABAAB Svv
LL
EI
S 




26
2

  F
BABABABA Mvv
LL
EI
M 




3
2
2
   F
BABABABA Svv
LL
EI
S 




26
2


9. Fixed End Moment/Shear
• MAB
F, MBA
F are fixed end moments at nodes A and B,
respectively.
• Moments at two ends of beam when beam is clamped at
both ends under external loading (see next slides)
• SAB
F, SBA
F are fixed end shears at nodes A and B,
respectively.
• Shears at two ends of beam when beam is clamped at both
ends under external loading (see next slides)
9

10. Fixed End Moment/Shear
10

11. Fixed End Moment/Shear
11

12. Example
• Find support reactions.
12

13. Solution
• This beam has 2 degrees
of indeterminacy
13
1- Assume all beams
are fixed & calculate
FEM
2- Establish Slope-
Deflection equations
3- Enforce boundary
conditions &
equilibrium conditions
at joints
4- Solve simultaneous
equations to get
slopes/deflections

14. Solution
14
kNmMM F
BA
F
AB 75.0
8
0.16


 kNmMM F
CB
F
BC 25.1
8
0.110


 kNmMM F
DC
F
CD 00.1
12
0.112 2




15. Solution
15
  F
ijjijiij Mvv
LL
EI
M 




3
2
2

  F
jijijiji Mvv
LL
EI
M 




3
2
2

vi=0 and vj=0 for all
cases

16. Solution
• Equilibrium moments at the joints
16
MBA MBC
MCB MCD
0ABM
0
0


BCBA
B
MM
M
0
0


CDCB
C
MM
M 0DCM

17. Solution
• Substitution into slope deflection equations gives 4
equations and 4 unknown slopes.
• By simultaneously solving the equations
17

18. Solution
• Simply operation of substitution:
18

19. Solution
• Now support reactions can easily be calculated as
19
15.485.16
85.1
0.1
15.15.06




BA
AB
R
R
6 10
25.575.410
75.4
0.1
4.115.15.010




CB
BC
R
R
12
6.44.712
4.7
0.1
4.15.012




DC
CD
R
R

20. Solution
20
1.85 4.15 4.75 5.25 7.4 4.6
1.85 8.9 12.65 4.60

21. Solution
21

22. Example 2
• Obtain moment reaction at the clamped
support B for 6m long beam if support A settles
down by 5mm. EI=17×1012 Nmm2
22
A
4kN/m
B

23. Solution
23
  F
ijjijiij Mvv
LL
EI
M 




3
2
2
   F
jijijiji Mvv
LL
EI
M 




3
2
2

A
4kN/m
5mm
B
  



 F
ABBABAAB Mvv
LL
EI
M
3
2
2

  






12
4000
0005.0
3
02
2
0
2
L
LL
EI
M AAB 
radL
L
EI
A
4
3
1033.9
2
0015.0
24
4000











24. Solution
24
A
4kN/m
5mm
B
  F
ijjijiij Mvv
LL
EI
M 




3
2
2
   F
jijijiji Mvv
LL
EI
M 




3
2
2

radA
4
1033.9 

  



 F
BABAABBA Mvv
LL
EI
M
3
2
2

  





 
12
4000
0005.0
3
1033.90
2 2
4 L
LL
EI
MBA
mNMBA .3.18705

25. Case study
25

26. Case study
26
t=3.552 mm
b=7.792 mm
  F
ijjijiij Mvv
LL
EI
M 




3
2
2


27. Case study
27
Rotation and displacement
can be obtained from the
FEM
Wire in composite beam

28. Case study
28
Rotation and displacement
can be obtained from the
FEM

29. Q1
• Determine the support reactions in the beam shown
below.
29

30. Q2
• Calculate the support reactions in the beam shown
below.
30

31. Q3
• Determine the end moments in the members of the
portal frame shown. The second moment of area of
the vertical members is 2.5I while that of the
horizontal members is I.
31

32. Q4
• Analyze two span continuous beam ABC by slope
deflection method. Then draw Bending moment & Shear
force diagram. Take EI constant.
32