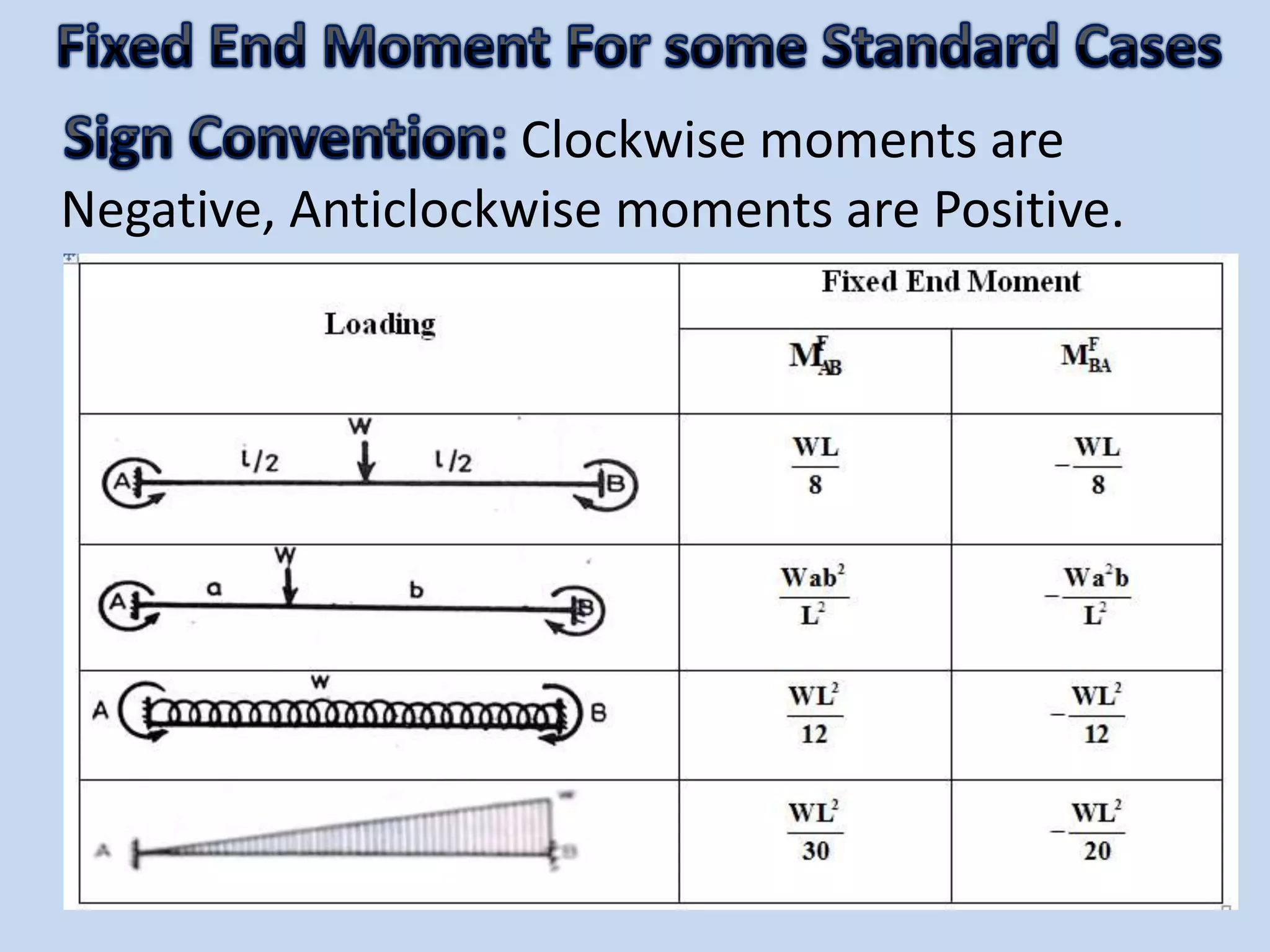
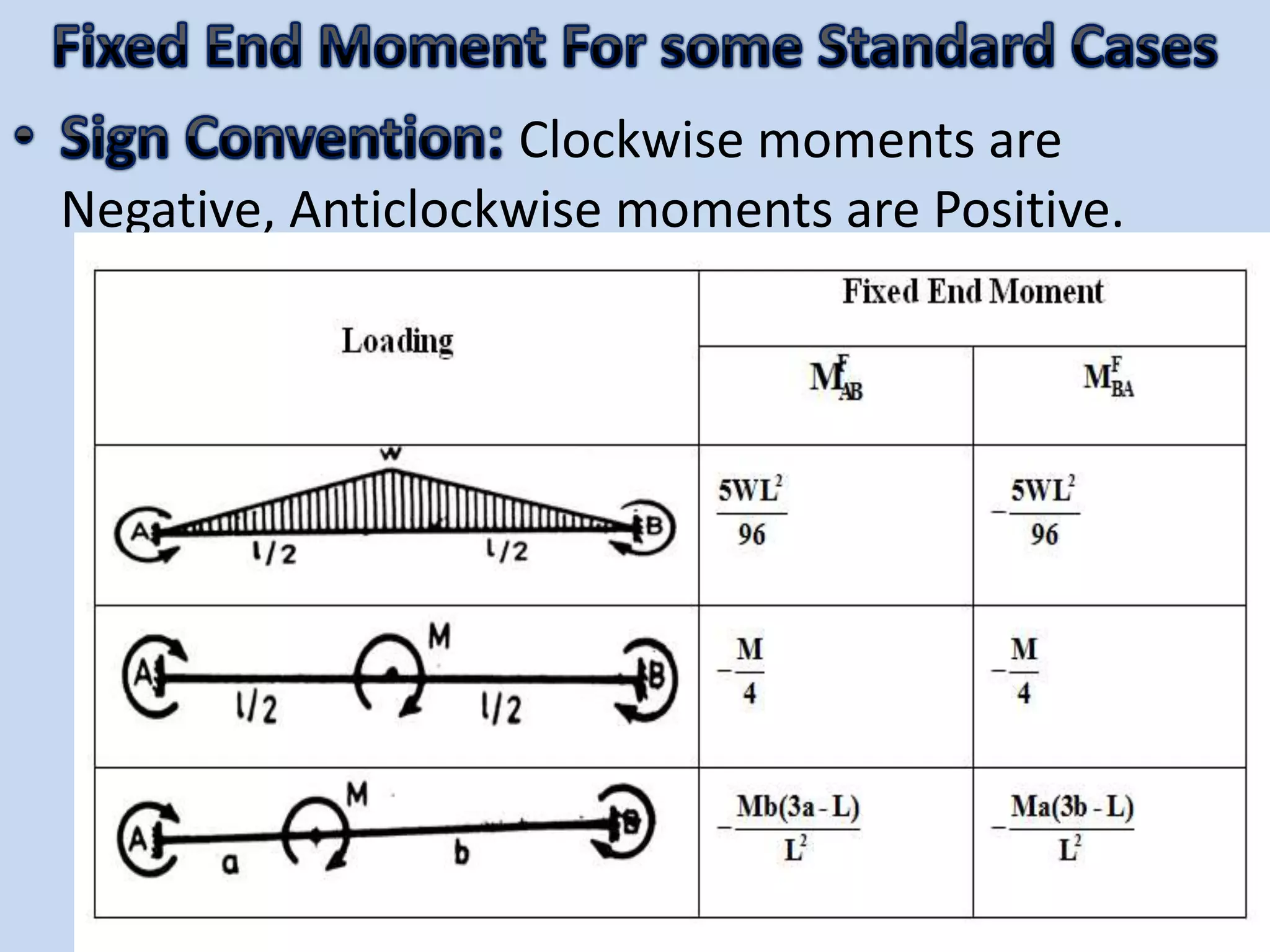
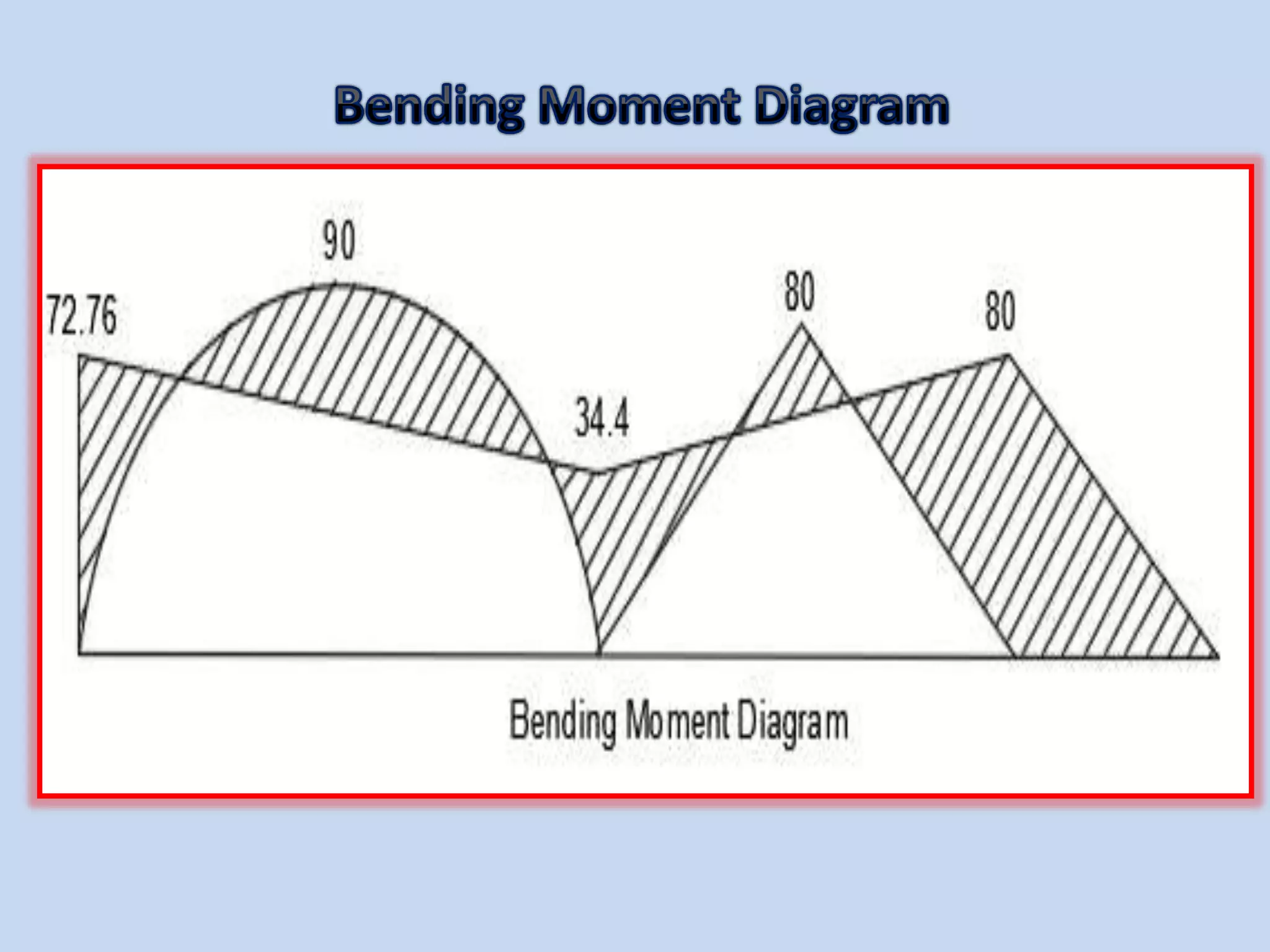
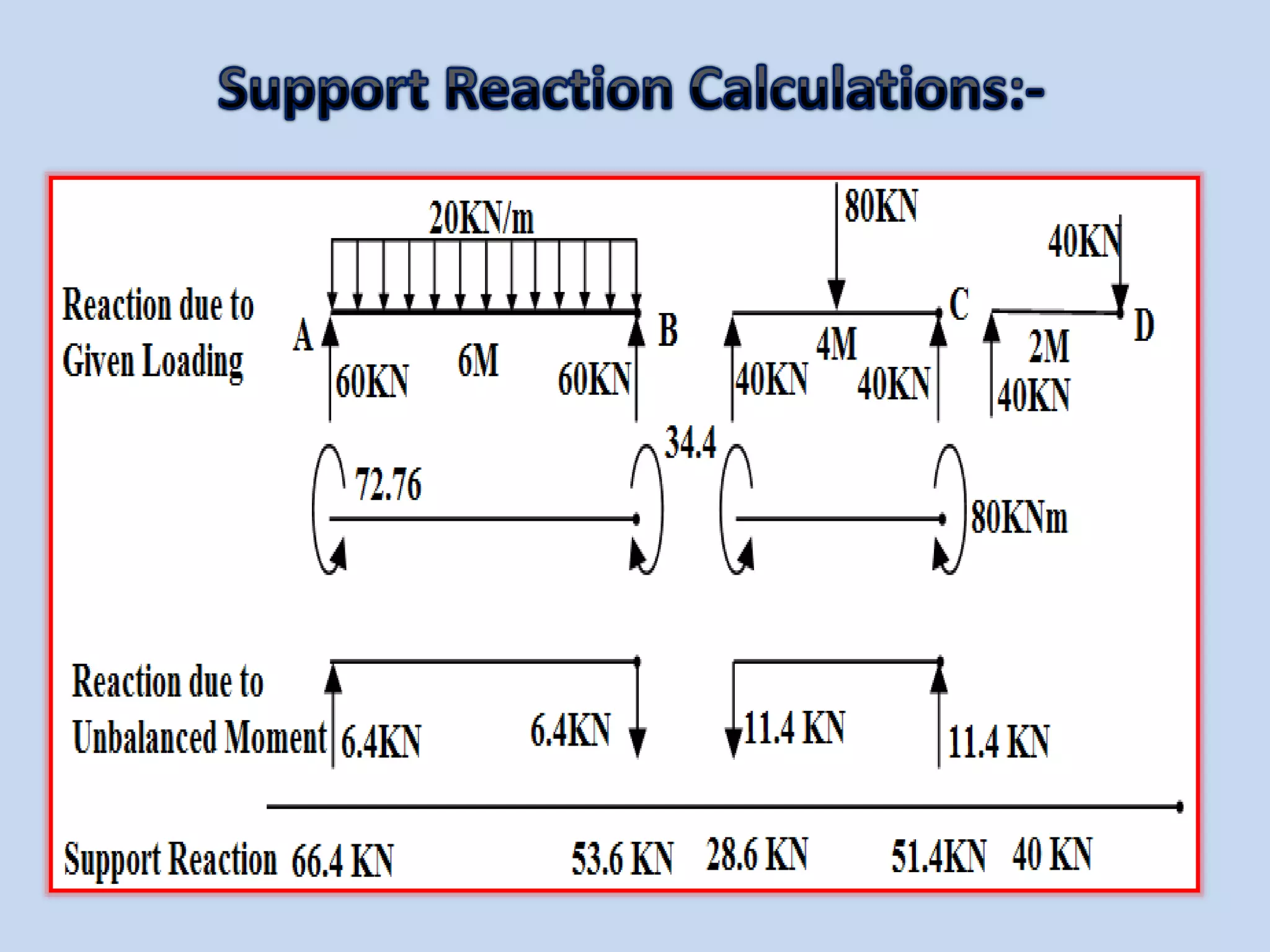
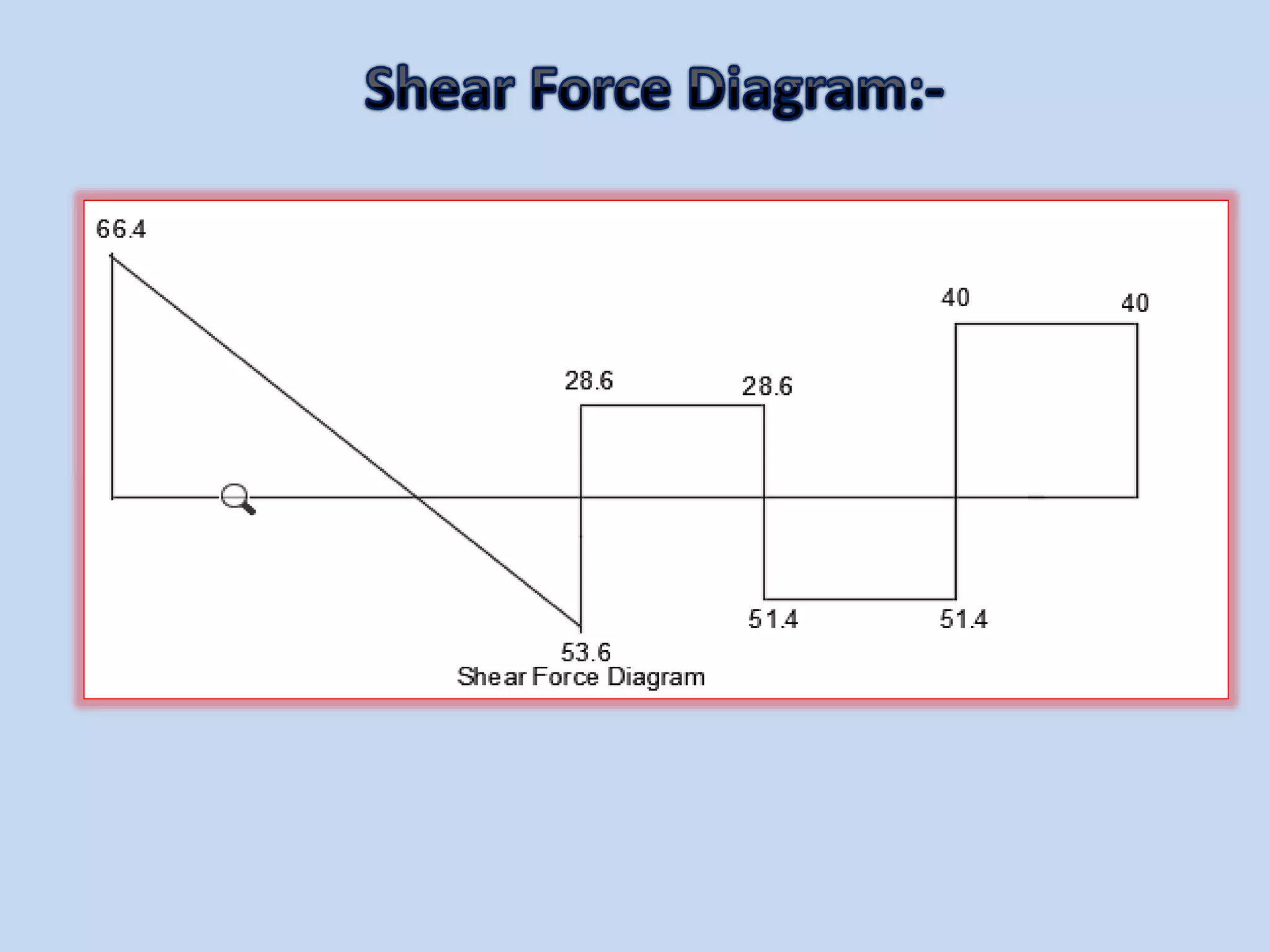
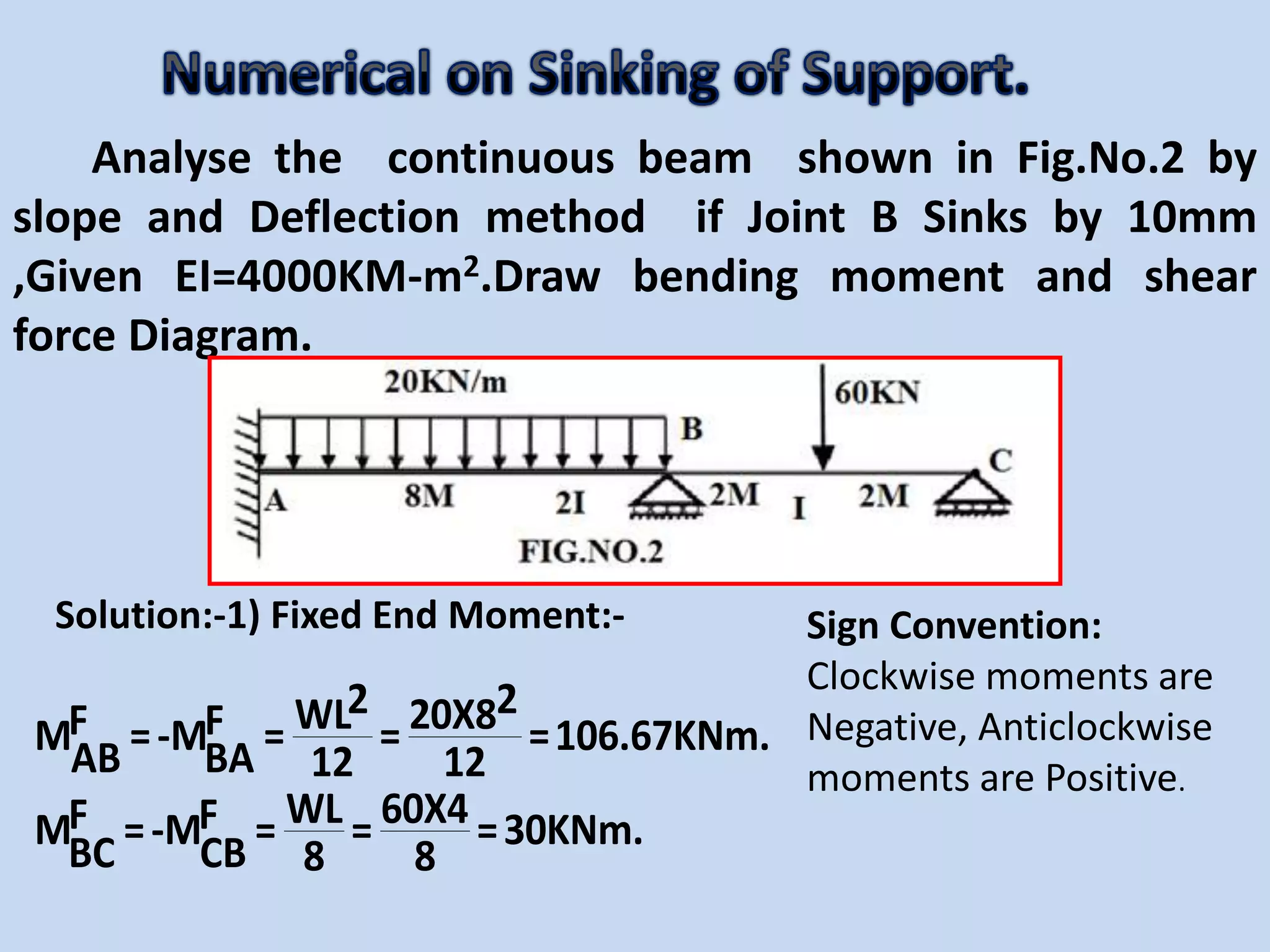
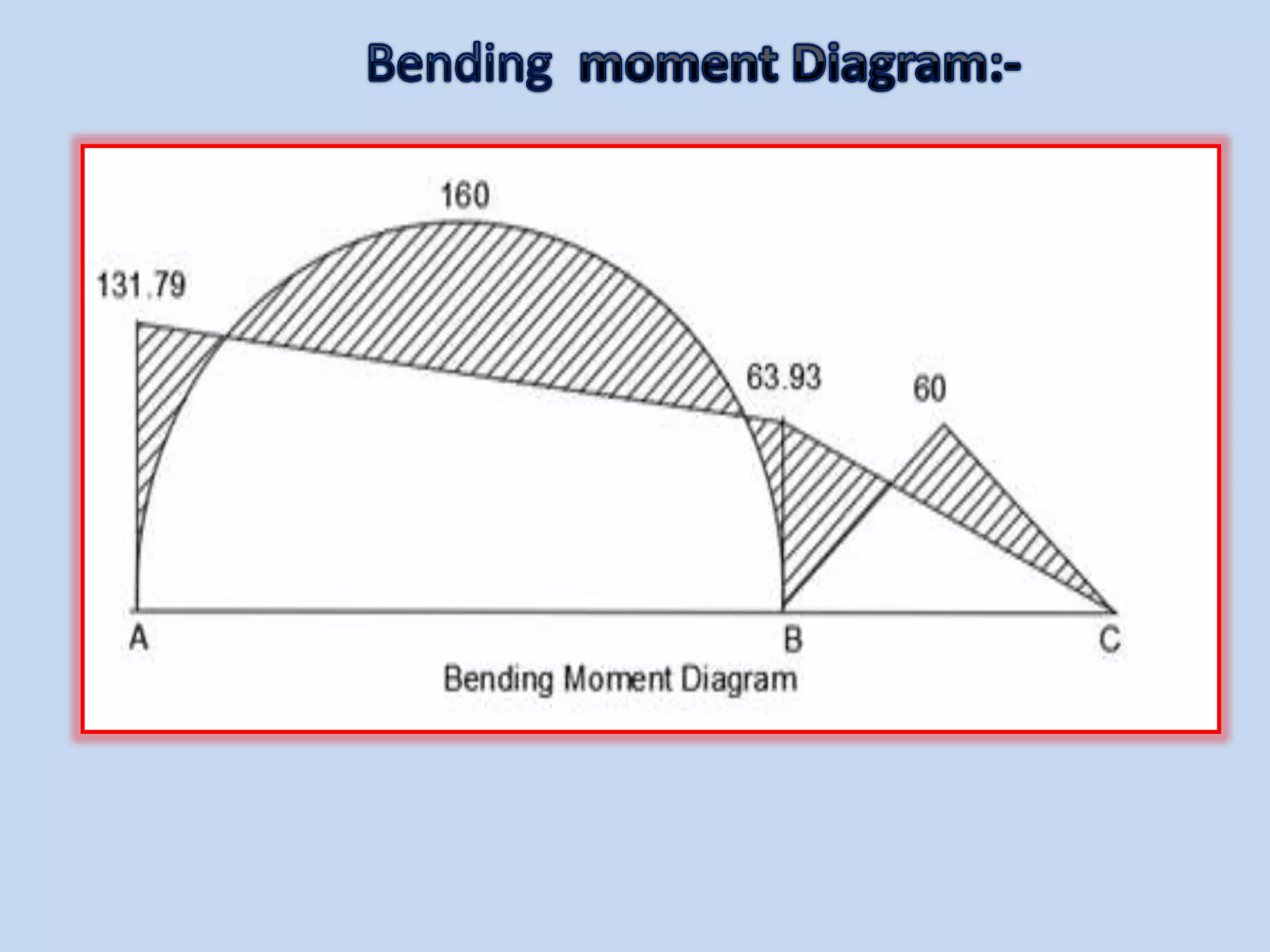
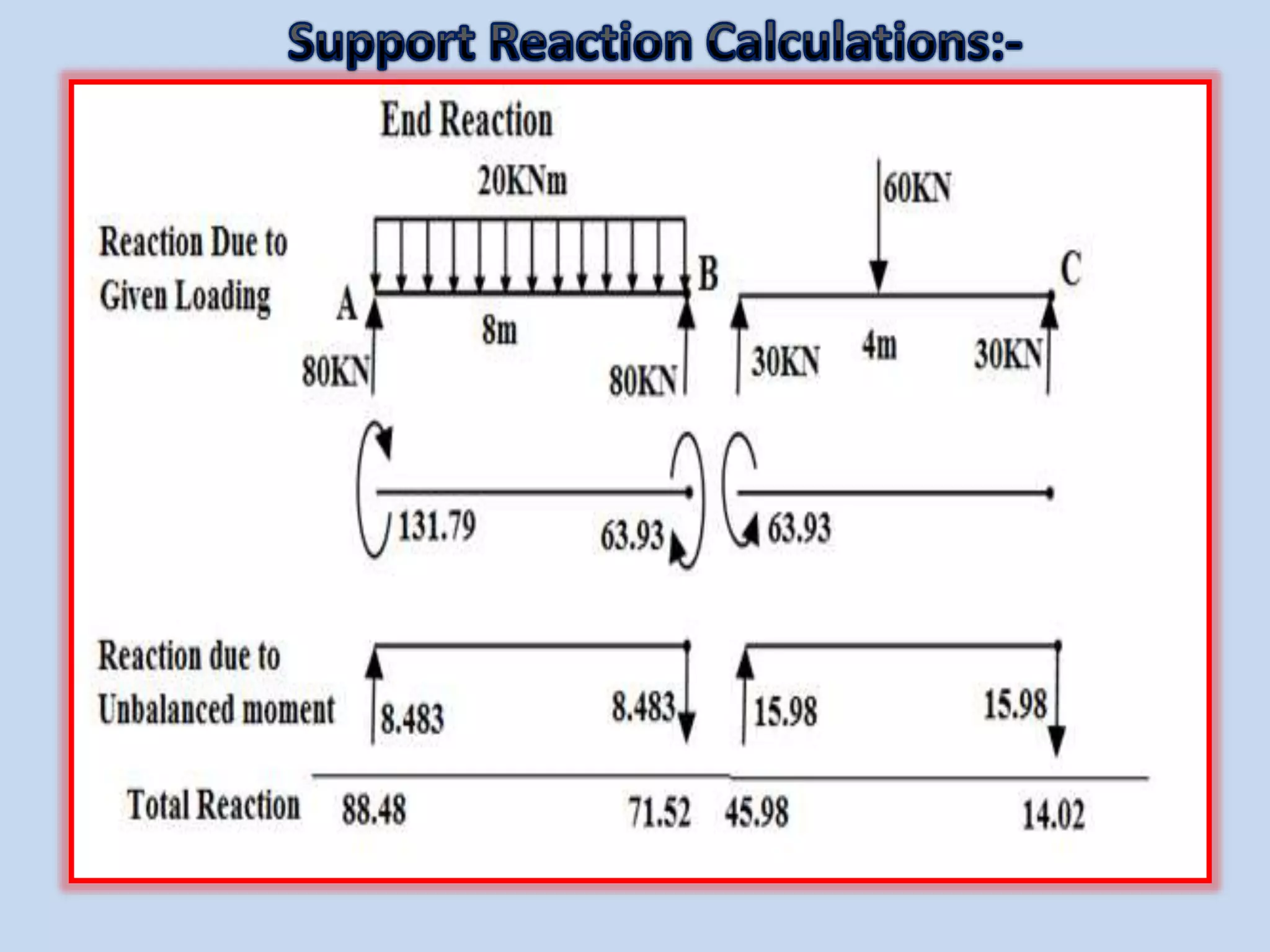
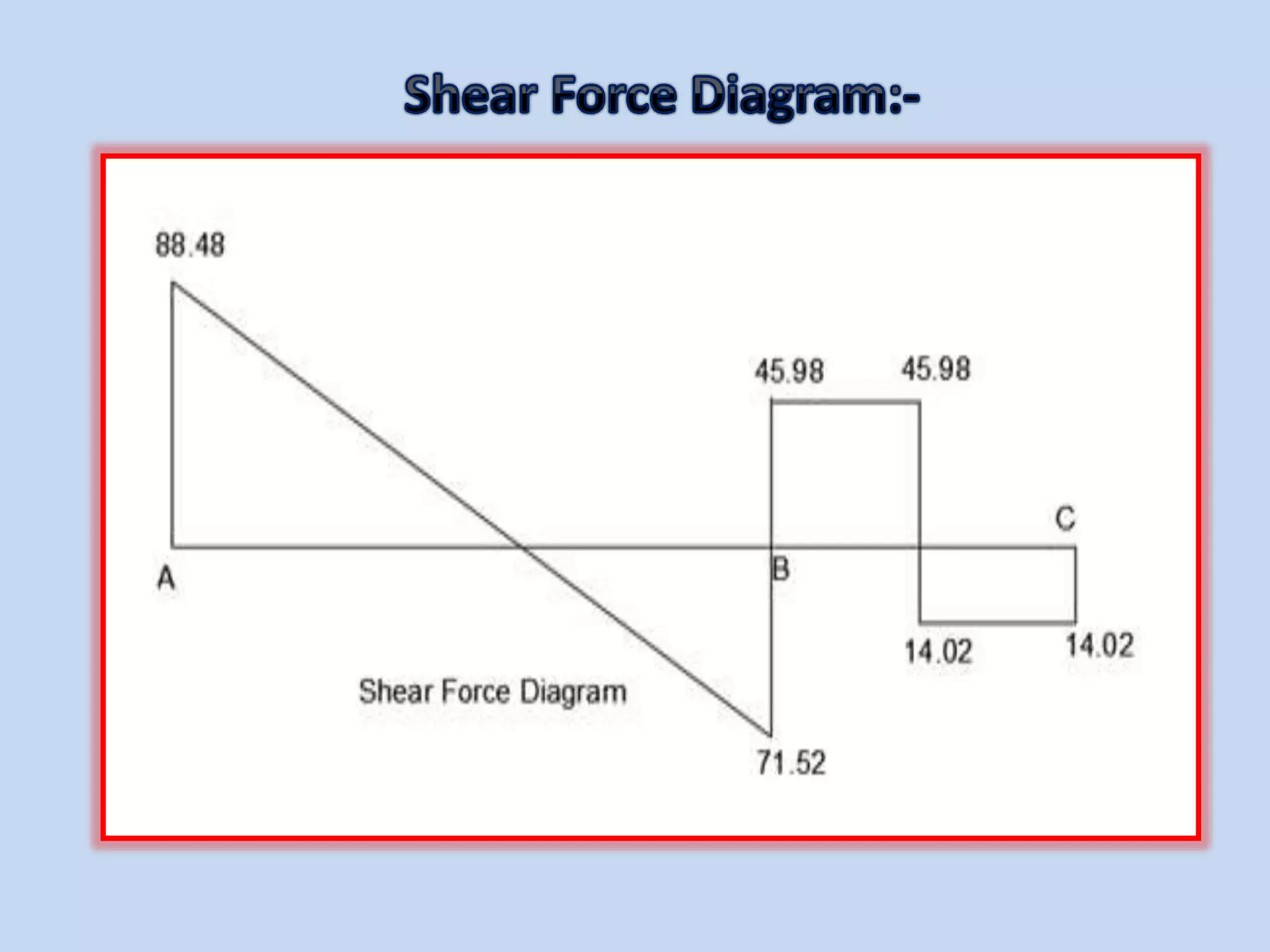
The slope deflection method, introduced by George A. Money in 1815, is utilized for analyzing statically indeterminate beams and frames, focusing on the slopes and deflections at joints. The method involves determining joint displacements to find fixed end moments and applying equations relating to these members. Example problems illustrate the application of this method for continuous beams, demonstrating the calculation of bending moments and shear forces.

2. • Slope Deflection Method was presented by George A
Money in 1815.
• Use to Analyse Statically Indeterminate Beams and
Frames.
• Slope Deflection method is a Displacement method i.e.
Equation Method.
• This Method mainly involves slope and Deflection of
the member at it’s joint and hence the named as Slope
deflection method.
• The Basic unknown in slope Deflection method are the
non zero joint displacement of a structure. i.e.., Degree
of Kinematic Indeterminacy (Degree of freedom).

3. Slope and Deflection Equation for member AB
F
AB AB A B 2
F
BA BA A B 2
4EI 2EI 6EI
M = M + Θ + Θ ± Δ
L L L
2EI 4EI 6EI
M = M + Θ + Θ ± Δ
L L L
FixedEndmomentduetoTransverseLoad.
NearEndRotatio
F FM =M =
AB BA
4EIΘ= ncontri
L
bution.
2EIΘ=
L
6EI
Far EndRotationcontribution.
Relative TranslationContributΔ=
2L
ion.

4. • ΘA= End slope at A or the rotation of the joint A.
• ΘB= End slope at B or the rotation of the joint B.
• ΔA=End deflection at A or the translation of Joint A.
• ΔB=End deflection at B or the translation of Joint B.
• ΔB/A=Relative Deflection or Translation of Joint B
with respect to A.
• MF
AB=Fixed end Moment at A for member AB.
• MF
BA=Fixed End moment at B for member BA.

5. Clockwise moments are
Negative, Anticlockwise moments are Positive.

6. Clockwise moments are
Negative, Anticlockwise moments are Positive.

7. 1)Analyse the Two span continuous beam shown in Fig.No.1 by slope
and Deflection method ,draw bending moment and shear force
Diagram.
Solution:- Fixed End Moment
2 2
F
AB
2 2
F
BA
F F
BC CB
CD
WL 20X6
M = = = 60KNm.
12 12
WL 20X6
M = - = - = -60KNm.
12 12
WL 80X4
M = -M = = = 40KNm.
8 8
M = 40X2 = 80KNm.
TotalRestrainedmoment at C = -40 + 80 = 40KNm.
Sign Convention: Clockwise
moments are Negative,
Anticlockwise moments are
Positive.

8. Application of slope and Deflection equation to
member AB
F
AB AB A B 2
AB B
A
AB B
F
BA BA A B 2
BA B
BA B
4EI 2EI 6EI
M = M + Θ + Θ ± Δ
L L L
2E(2I)
M = 60+ Θ
6
(Astheiris fixedsupportat A,soΘ = 0&noSinking of support,so Δ = 0)
2EI
M = 60+ Θ ------(I).
3
2EI 4EI 6EI
M = M + Θ + Θ ± Δ
L L L
4E(2I)
M = -60+ Θ .
6
4EI
M = -60+ Θ -
3
-----(II)

9. Application of slope and Deflection equation to
member BC
F
BC BC B C 2
BC B C
BC B C
F
CB CB B C 2
CB B C
CB B C
4EI 2EI 6EI
M = M + Θ + Θ ± Δ.
L L L
4EI 2EI
M = 40 + Θ + Θ .
4 4
M = 40 + EIΘ + 0.5EIΘ .- - - - - - - (III)
2EI 4EI 6EI
M = M + Θ + Θ ± Δ.
L L L
2EI 4EI
M = -40 + Θ + Θ .
4 4
M = -40 + 0.5EIΘ + EIΘ .- - - - - - - - - (IV).

10.  C
CB CD
B C
B C
M = 0.
M + M = 0.
-40 + 0.5EIΘ + EIΘ + 80 = 0
0.5EIΘ + EIΘ = -40 - - - - - - (2)
M = 0.B
M +M = 0.BA BC
4EI
-60+ Θ + 40+EIΘ + 0.5EIΘ = 0B B C3
2.34EIΘ + 0.5EIΘ = 20 - - - - - (1)B C
solving Equation1 and2
we get,
19.14Θ =B EI
-49.56Θ =
C EI

11. Substituting the values of in slope deflection equation
2EIM = 60 + ΘAB B3
2M = 60 + 19.14.AB 3
M = 72.76 KNm.AB

4EIM = -60 + ΘBA B3
4M = -60 + X19.14BA 3
M = -34.4 KNm.BA

12. M = 40+EIΘ +0.5EIΘBBC C
M = 40+19.14+0.5X(-49.56)
BC
M =34.36KNm.
BC
Substituting the values of in slope deflection equation
M =-40+0.5EIΘ +EIΘ .
BCB C
M =-40+0.5(19.14)+(-49.56)
CB
M =-80KNm.
CB
M =80KNm.
CD

16. Analyse the continuous beam shown in Fig.No.2 by
slope and Deflection method if Joint B Sinks by 10mm
,Given EI=4000KM-m2.Draw bending moment and shear
force Diagram.
Solution:-1) Fixed End Moment:-
2 2WL 20X8F FM =-M = = =106.67KNm.AB BA 12 12
WL 60X4F FM =-M = = =30KNm.
BC CB 8 8
Sign Convention:
Clockwise moments are
Negative, Anticlockwise
moments are Positive.

17. 4EI 2EI 6EIFM =M + Θ + Θ ± ΔAB AB A B 2L L L
2E(2I) 6X4000X2 10M =106.67+ Θ + XAB B 28 10008
(As their is fixedsupport at A,so Θ = 0)A
M =106.67+0.5EIΘ +7.5AB B
M =114.17+0.5EIΘ ------ (I).AB B
2EI 4EI 6EIFM =M + Θ + Θ ± ΔBA BA A B 2L L L
M = -106.67+BA
4E(2I) 6X4000X2 10Θ + X .B 28 10008
M = -99.17+EIΘ ------ (II)BA B
Application of slope and Deflection equation to member AB

18. Application of slope and Deflection equation to member BC
4EI 2EI 6EIFM =M + Θ + Θ ± Δ.
BBC BC CL L 2L
4EI 2EI 6X4000 10M =30+ Θ + Θ - X .
BBC C4 4 2 10008
M =15+EIΘ +0.5EIΘ .-------(III)
BBC C
2EI 4EI 6EIFM =M + Θ + Θ ± Δ.
BCB CB CL L 2L
2EI 4EI 6X4000 10M =-30+ Θ + Θ - X .
BCB C4 4 2 10008
M =-45+0.5EIΘ +EIΘ .---------
BCB C
(IV).

19. M = 0.
B
M +M = 0.
BA BC
-99.17+EIΘ +15+EIΘ +0.5EIΘ = 0
B B C
2EIΘ +0.5EIΘ = 84.17 ----- (1)
B C
M =0.
C
M =0.
CB
0.5EIΘ +EIΘ = 45 ------ (2)
B C
Solving Equation1 and2
we get,
EIΘ =35.24
B
EIΘ =27.38
C

20. M =114.17+0.5EIΘ
AB B
M =114.17+0.5 X 35.24
AB
M =131.79KNm.
AB
M = -99.17+EIΘ
BA B
M = -99.17+35.24
BA
M = -63.93KNm.
BA
M = 15+EIΘ +0.5EIΘ .
BBC C
M = 15+35.24+0.5X27.38.
BC
M = 63.93KNm.
BC
M = -45+0.5EIΘ +EIΘ .
BCB C
M = -45+0.5X35.24+27.38
CB
M = 0
CB