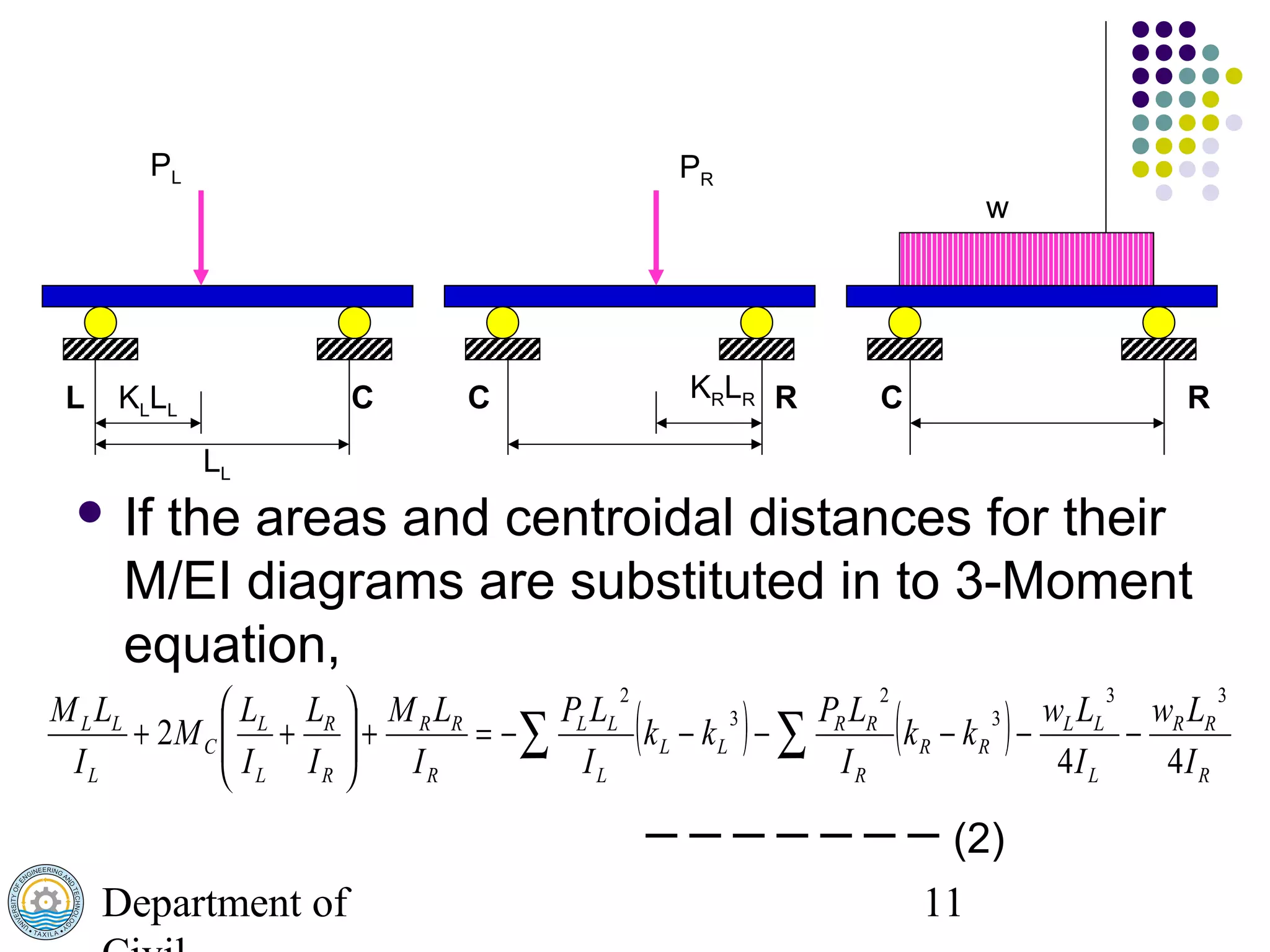
The document discusses the three moment equation theory of structure analysis. [1] It relates the internal moments in a continuous beam at three points of support to the applied loads between supports. [2] The theory is proved using the conjugate beam method by equating shear forces and summing moments. [3] The general three moment equation is developed and modified for common load cases like point and uniform loads. An example problem demonstrates solving for reactions at supports.

1. Three Moment
Equation
Theory of Structure - I
Department of Civil Engineering
University of Engineering and Technology, Taxila, Pakistan

2. Lecture Outlines
 Introduction
 Proof of Three Moment Equation
 Example
Department of 2

3. Introduction
 Developed by French Engineer Clapeyron in
1857.
 This equation relates the internal moments in
a continuous beam at three points of support
to the loads acting between the supports.
 By successive application of this equation
to each span of the beam, one obtains a set
of equations that may be solved
simultaneously for the unknown internal
moments at the support.
Department of 3

4. Proof: Real Beam
A general form of three moment equation can
be developed by considering the span of a
continuous beam.
P1 P2 P3 P4
WL WR
ML MC MC MR
L C R
LL LR
Department of 4

5. Conjugate Beam (applied
loads)
 The formulation will be based on the
conjugate-beam method.
 Since the “real beam” is continuous over the
supports, the conjugate-beam has hinges at
L, C and R.
AL /EIL AR /EIR
L’ LL CL 1 CR 1 LR R’
XL XR
Department of 5

6. Conjugate Beam (internal
moments)
 Usingthe principle of superposition, the M /
EI diagram for the internal moments is
shown.
MC /EIL
MR /EIR
ML /EIL MC /EIR
L’ LL CL2 CR2 LR R’
Department of 6

7.  In particular AL/EIL and AR/EIR represent the
total area under their representative M / EI
diagrams; and xL and xR locate their centroids.
 Since the slope of real beam is continuous
over the center support, we require the shear
forces for the conjugate beam.
C L1 + C L2 = −(C R1 + C R2 )
Department of 7

8.  Summing moments about point L’ for left
span, we have
1 AL 1 1  M L  1  1  M  2 
C L1 + C L2 = ( xL ) +   ( LL ) LL  +  C ( LL ) LL 
LL EI L LL 2  EI L
 



 3  2  EI L

 3 
AL xL M L LL M C LL
= + +
EI L 6 EI L 3EI L
 Summing moments about point R’ for the
right span yields
1 AR 1 1  M R  1  1  M  2 
C R1 + C R2 = ( xR ) +   ( LR ) LR  +  C ( LR )  LR 
LR EI R LR 2  EI R
 



 3  2  EI R

 3 
AR xR M R LR M C LR
= + +
EI R 6 EI R 3EI R
Department of 8

9. General Equation
 Equating
C L1 + C L2 = −(C R1 + C R2 )
 and simplifying yields
M L LL  LL LR  M R LR 6 AL xL 6 AR xR
+ 2M C  +  +
I  = −∑ −∑
IL  L IR  IR I L LL I R LR
(1)
Department of 9

10. Eq. Modification for point load
and uniformly distributed load
 Summation signs have been added to the
terms on the right so that M/EI diagrams for
each type of applied load can be treated
separately.
 In practice the most common types of
loadings encountered are concentrated and
uniform distributed loads.
Department of 10

11. PL PR
w
L KLLL C C KRLR R C R
LL
 If the areas and centroidal distances for their
M/EI diagrams are substituted in to 3-Moment
equation,
 LL LR  M R LR
( ) ( )
2 2 3 3
M L LL PL LL PR LR wL LL wR LR
+ 2M C  +  + = −∑ kL − kL − ∑
3 3
I  kR − kR − −
IL  L IR  IR IL IR 4I L 4I R
(2)
Department of 11

12. Special Case:
 If the moment of inertia is constant for the
entire span, IL = IR.
( ) ( )
3 3
wL LL wR LR
M L LL + 2M C ( LL + LR ) + M R LR = − ∑ PL LL k L − k L − ∑ PR LR k R − k R
2 3 2 3
− −
4 4
(3)
Department of 12

13. Example:
 Determinethe reactions at the supports for
the beam shown. The moment of inertia of
span AB is one half that of span BC.
3 k/ft
15k
A C
0.5 I B I
25 ft 15 ft 5 ft
Department of 13

14. Data
M =0 M = MB M =0
L C R
L = 25ft L = 20ft
L R
I = 0.5I I =I
L R
P =0 P = 15k
L R
w = 3k/ft w =0
L R
k =0 k = 0.25
L R
Department of 14

15.  Substituting the values in equation 2,
 25 20 
0 + 2M B  + +0 = 0−∑
15 * 20 2
(
0.25 − 0.253 − )
3 * 253
−0
 0.5I I  I 4 * 0.5I
M B = −177.5k . ft
Department of 15

16.  For span AB:
∑ F = 0; A
x x =0
75 k
∑ M = 0;B
− Ay (25) − 177.5 + 75(12.5) = 0
VBL
Ay = 30.4k
A B
∑F y = 0;
Ay
12.5’ 12.5’ 177.5k.ft
30.4 − 75 + VBL = 0
VBL = 44.6k
Department of 16

17.  For span BC:
∑M B = 0;
15 k
C y (20) + 177.5 + 15(15) = 0
C y = 2.38k VBR
∑F y = 0; B
15 ft 5 ft
C
177.5k.ft
2.38 − 15 + VBR = 0 Cy
VBR = 12.6k
Department of 17

18. A free body diagram of the differential
segment of the beam that passes over roller
at B is shown in figure.
∑F y =0 177.5k.ft 177.5k.ft
B y − 44.6 − 12.6 = 0
B y = 57.2k 44.6 k 12.6 k
By
Department of 18

19. Practice Problems:
 Chapter 9
 Example 9-11 to 9-13 and Exercise
 Structural Analysis by R C Hibbeler
Department of 19

20. Department of 20