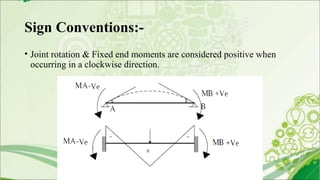
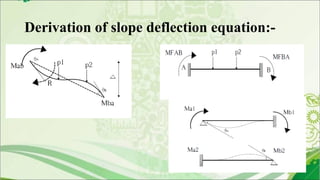
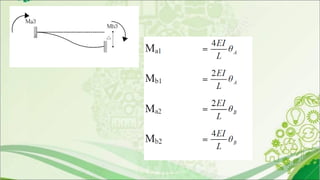
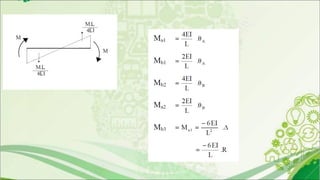
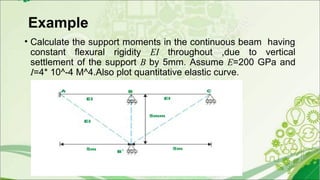
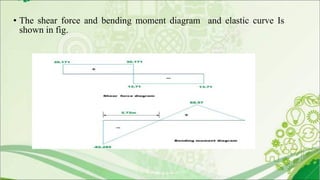
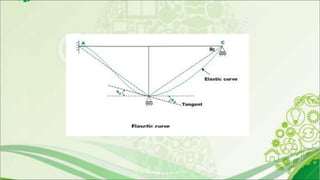
1. The document discusses the slope deflection method of structural analysis, which uses displacements as unknowns rather than forces. 2. The method is based on assumptions that joints are rigid and axial/shear distortions are negligible. 3. Derivation of the slope deflection equations involves determining fixed end moments and correcting for end rotations and member rotation from applied loads. 4. An example problem is presented to calculate support moments in a continuous beam due to vertical settlement of one support, by setting up and solving slope deflection equations.

1. Subject Name: Theory of
Structures
Topic Name:Deflection of Beams
Lecture No: 10
Dr.Omprakash Netula
Professor & HOD
Department of Civil Engineering
07/24/17 Lecture Number, Unit Number 1

2. Deflection of Beams
• Introduction
• Assumptions
• Sign conventions
• Derivation of slope deflection method
• Example

3. Introduction
• The methods of three moment equation, and consistent deformation
method represent the FORCE METHOD of structural analysis, The
slope deflection method use displacements as unknowns, hence this
method is the displacement method.
• In this method, if the slopes at the ends and the relative displacement
of the ends are known, the end moment can be found in terms of
slopes, deflection, stiffness and length of the members.

4. ASSUMPTIONS IN THE SLOPE
DEFLECTION METHOD
• This method is based on the following simplified assumptions.
• 1- All the joints of the frame are rigid, i.e , the angle between the
members at the joints do not change, when the members of frame are
loaded.
• 2- Distortion, due to axial and shear stresses, being very small, are
neglected.

5. Sign Conventions:-
• Joint rotation & Fixed end moments are considered positive when
occurring in a clockwise direction.

6. Derivation of slope deflection equation:-

8. • Required Mab
&M
ba
intermof
• θA
, θ
B
atjoint
• rotation of member (R)
• loads acting on member
• First assume ,
• Get Mfab & Mfba due to acting loads. These fixed end moment must be
corrected to allow for the end rotations θA,θB and the member rotation
R.
• The effect of these rotations will be found separately

10. • by Superposition;

11. Example
• Calculate the support moments in the continuous beam having
constant flexural rigidity EI throughout ,due to vertical
settlement of the support B by 5mm. Assume E=200 GPa and
I=4* 10^-4 M^4.Also plot quantitative elastic curve.

12. • In the continuous beam, two rotations Bθ and Cθ need to be evaluated.
Hence, beam is kinematically indeterminate to second degree. As there
is no external load on the beam, the fixed end moments in the
restrained beam are zero.

13. • For each span, two slope-deflection equations need to be written. In
span AB, B is below A. Hence, the chord AB rotates in clockwise
direction. Thus,ABψ is taken as negative.

14. Now, consider the joint equilibrium of support B

16. Reactions are obtained from equations of static equilibrium

18. • The shear force and bending moment diagram and elastic curve Is
shown in fig.