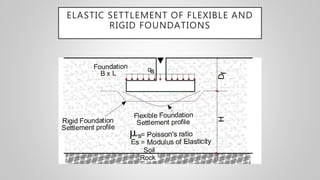
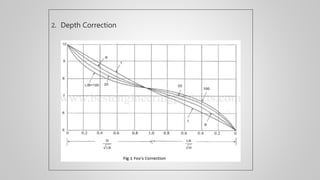
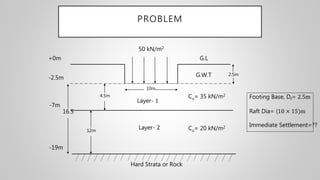
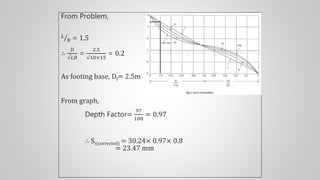
The document discusses immediate settlement in foundations, especially for shallow footings on sandy bases, and provides the formula for calculating immediate settlement using parameters such as net foundation pressure, foundation width, Poisson's ratio, and Young's modulus of soil. It explains the differences in settlement for flexible and rigid foundations, emphasizing the need to calculate the influence factor for various footing shapes. Additionally, it outlines corrections for rigidity and depth in determining settlement values.

1. DETERMINATION OF IMMEDIATE
SETTLEMENT
Suez Halder
Email: suez_301@yahoo.com
By

2. SIMPLIFIED DEFINITION
When the settlement of the footing takes place
immediately after the load is applied over the footing, it
is termed as immediate settlement.
When Occurs?
Immediate settlement occurs in the case of shallow
footings, having sand as base of the footing.

3. IMMEDIATE SETTLEMENT CALCULATION
According to the theory of elasticity,
Si=
𝑞𝐵
𝐸
1 − µ2 If
Where,
q= Net foundation pressure
B= Width of the foundation
𝜇= Poisson’s ration
E= Young’s modulus of soil
If= Influence factor

4. SIGNIFICANCE OF INFLUENCE FACTOR
(If)
We have to calculate Influence Factor (If) for different
shapes of footing, i.e. square, circular, rectangular and
for different types of foundation. Such as-
1. Flexible type foundation. Ex: Isolated Footing
2. Rigid Type Foundation. Ex: Raft or Matt Foundation

5. ELASTIC SETTLEMENT OF FLEXIBLE AND
RIGID FOUNDATIONS

6. EXPLANATION
For Flexible Foundation-
Settlement value at the corner of the footing and the center of the
footing are not the same. Here, settlement value of the center is
more than the corner of the foundation. So we have to calculate
influence factor individually for corner and center. Also we have to
calculate the average If .
For Rigid Foundation-
The settlement value is uniform throughout corner and center. So
the influence factor (If ) will be 1.0
It is observed that-
At center,
Flexible Foundation Settlement > Rigid Foundation
Settlement

7. INFLUENCE FACTORS FOR
FOUNDATIONS
Influence Factor, 𝑰 𝒑
Flexible
Shape 𝐿
𝐵
Center Corner Rigid
Circle ---- 1.00 0.64 0.79
Square 1 1.12 0.56 0.88
Rectangle 1.5 1.36 0.68 1.07
2 1.53 0.77 1.21
3 1.78 0.89 1.42
5 2.10 1.05 1.70
10 2.54 1.27 2.10
20 2.99 1.49 2.46
50 3.57 1.80 3.00
100 4.01 2.00 3.43

8. TWO TYPES OF CORRECTIONS
1. Rigidity Correction (for rigid foundation)
If for Rigid Foundation= 0.8 × If for the Flexible Foundation at
Center
We have to first calculate the settlement considering the
influence factor of the flexible foundation at the center, then
we will multiply that settlement calculation by 0.8 and will
get settlement of rigid foundation.

9. 2. Depth Correction

10. PROBLEM
+0m
-2.5m
-7m
-19m
50 kN/m2
G.L
G.W.T
10m
4.5m
12m
16.5
2.5m
Cu= 35 kN/m2
Cu= 20 kN/m2
Layer- 1
Layer- 2
Footing Base, Df= 2.5m
Raft Dia= (10 × 15)m
Immediate Settlement=??
Hard Strata or Rock

11. SOLUTION
Given,
qn= 50 kN/m2, B= 10m, 𝜇= 0.5 (for clay)
and E= 700 Cu
We know,
Si=
qn 𝐵
𝐸
1 − µ2 Ip
From figure, 𝐿
𝐵 =
15
10
= 1.5 So, If = 1.6 (center for flexible
foundation)
Again given,
For Layer-1: Cu= 35 kN/m2
For Layer-2: Cu= 20 kN/m2

12. ∴ E1= 700 × 35= 24500 kN/m2
And, E2= 700 × 20= 14000 kN/m2
∴ Weighted Eavg=
24500×4.5 +14000×12
16.5
= 16864 kN/m2
From Equation,
Si=
50×10
16864
(1 − 0.52) × 1.36 = 30.24 (without
correction)
We Know,
Rigidity Correction Factor= 0.8
Depth Correction Factor= ??

13. From Problem,
𝐿
𝐵 = 1.5
∴
𝐷
√𝐿𝐵
=
2.5
√10×15
= 0.2
As footing base, Df= 2.5m
From graph,
Depth Factor=
97
100
= 0.97
∴ Si(corrected) = 30.24× 0.97× 0.8
= 23.47 mm