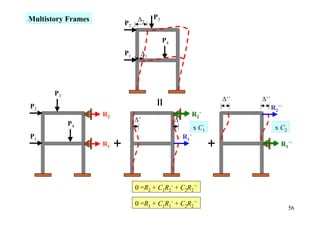
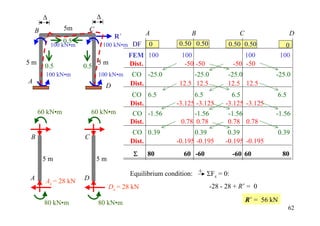
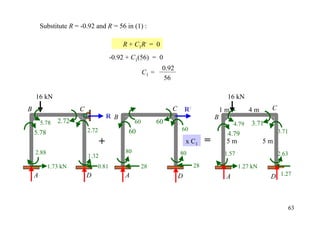
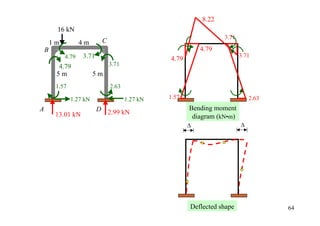
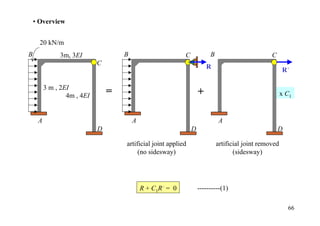
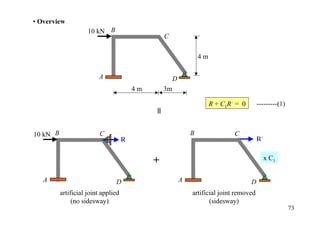
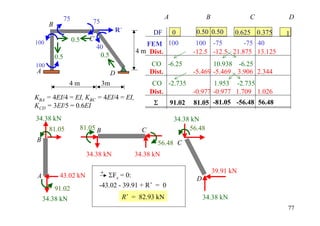
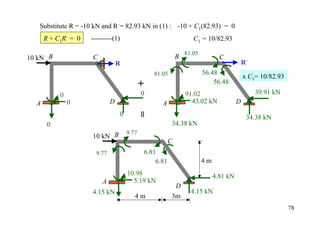
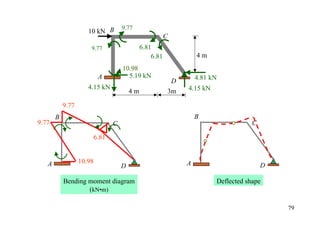
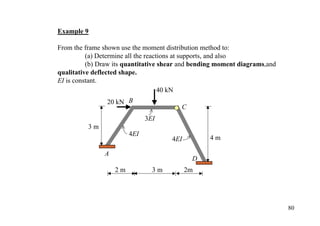
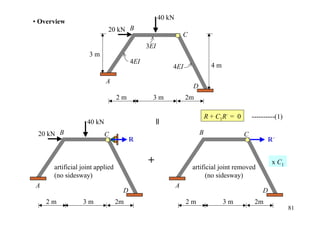
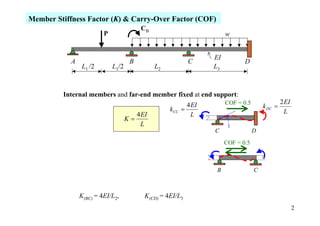
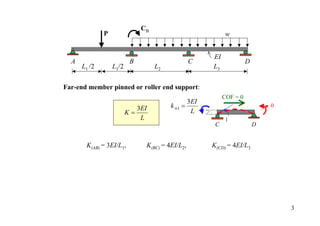
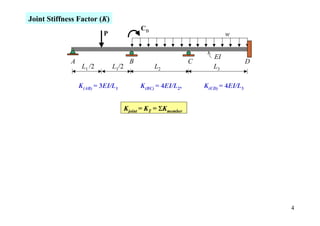
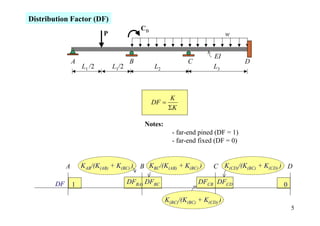
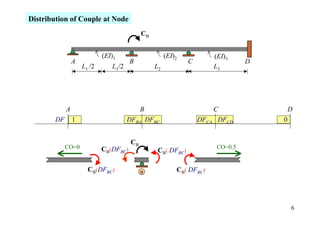
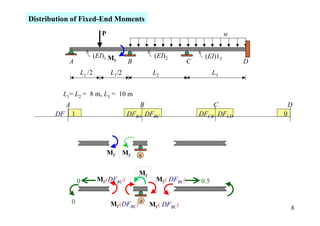
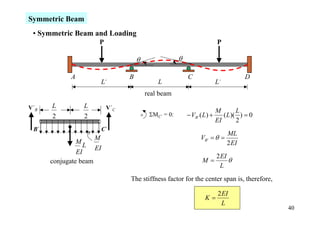
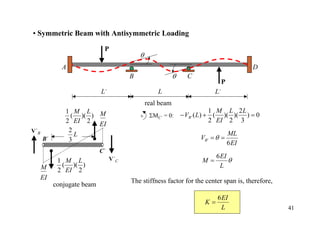
The document outlines the moment distribution method of structural analysis, detailing calculations for member stiffness factors, joint stiffness factors, and distribution factors. It includes examples of applying this method to analyze beams and frames, assessing reactions at supports, and generating shear and bending moment diagrams. Additionally, it provides formulas for fixed-end moments and adjustments for factors such as sidesway in frames.

1. DISPLACEMENT MEDTHOD OF ANALYSIS:
MOMENT DISTRIBUTION
! Member Stiffness Factor (K)
! Distribution Factor (DF)
! Carry-Over Factor
! Distribution of Couple at Node
! Moment Distribution for Beams
! General Beams
! Symmetric Beams
! Moment Distribution for Frames: No Sidesway
! Moment Distribution for Frames: Sidesway
1

2. Member Stiffness Factor (K) & Carry-Over Factor (COF)
CB
P w
EI
A B C D
L1 /2 L1/2 L2 L3
Internal members and far-end member fixed at end support:
4 EI COF = 0.5 2 EI
kCC = k DC =
4 EI L L
K=
L 1
C D
COF = 0.5
B C
K(BC) = 4EI/L2, K(CD) = 4EI/L3
2

3. CB
P w
EI
A B C D
L1 /2 L1/2 L2 L3
Far-end member pinned or roller end support:
COF = 0
3EI
3EI k AA = 0
K= L
L 1
C D
K(AB) = 3EI/L1, K(BC) = 4EI/L2, K(CD) = 4EI/L3
3

4. Joint Stiffness Factor (K)
CB
P w
EI
A B C D
L1 /2 L1/2 L2 L3
K(AB) = 3EI/L1 K(BC) = 4EI/L2, K(CD) = 4EI/L3
Kjoint = KT = ΣKmember
4

5. Distribution Factor (DF)
CB
P w
EI
A B C D
L1 /2 L1/2 L2 L3
K
DF =
ΣK
Notes:
- far-end pined (DF = 1)
- far-end fixed (DF = 0)
A KAB/(K(AB) + K(BC) ) B KBC/(K(AB) + K(BC) ) C K(CD)/(K(BC) + K(CD) ) D
DF 1 DFBA) DFBC DFCB DFCD 0
K(BC)/(K(BC) + K(CD) )
5

6. Distribution of Couple at Node
CB
(EI)1 (EI)2 (EI)3
A B C D
L1 /2 L1/2 L2 L3
A B C D
DF 1 DFBA DFBC DFCA DFCD 0
CB
CO=0 CB(DFBC) CO=0.5
CB( DFBC)
CB(DFBC) B CB( DFBC)
6

7. 50 kN•m
2EI 3EI 3EI
A B C D
4m 4m 8m 8m
L1= L2 = L3
A B C D
DF 1 0.333 0.667 0.5 0.5 0
50 kN•m
CO=0 CO=0.5
50(.667) 50(.667) 16.67
50(.333)
50(.333) B
7

8. Distribution of Fixed-End Moments
P w
(EI)1 M (EI)2 (EI)13
A F B C D
L1 /2 L1/2 L2 L3
L1= L2 = 8 m, L3 = 10 m
A B C D
DF 1 DFBA DFBC DFCB DFCD 0
MF MF B
MF
0 MF(DFBC) MF( DFBC) 0.5
0 MF(DFBC) B MF( DFBC)
8

9. P w
EI
A 1.5PL1/8=30 B wL22/12=16 C wL32/12=25 D
L1 /2 L1/2 L2 L3
L1= L2 = 8 m, L3 = 10 m
A B C D
DF 1 0.4 0.6 0.5 0.5 0
14
30 30 B 16 16
14
0 5.6 5.6 0.5 4.2
0 B 8.4 8.4
9

10. Moment Distribution for Beams
10

11. Example 1
The support B of the beam shown (E = 200 GPa, I = 50x106 mm4 ).
Use the moment distribution method to:
(a) Determine all the reactions at supports, and also
(b) Draw its quantitative shear and bending moment diagrams,and qualitative
deflected shape.
20 kN 3 kN/m
2EI 3EI
A B C
4m 4m 8m
11

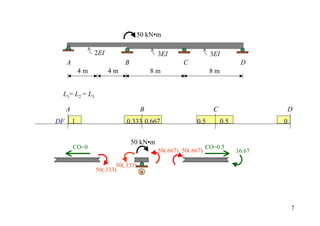
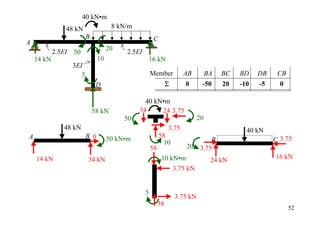
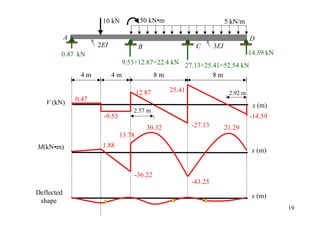
12. 20 kN 3 kN/m
2EI 3EI
30 16 16
A B C
CO 0.5 0 0.5 0
4m 4m 8m
K1 = 3(2EI)/8 K2 = 4(3EI)/8
K1/(K1+ K2) K2/(K1+ K2)
DF 1 0.333 0.667 0
[FEM]load -30 16 -16
Dist. 4.662 9.338
CO 4.669
Σ -25.34 25.34 -11.33
20 kN 24 kN
A B B C
25.34 kN•m 11.33 kN•m
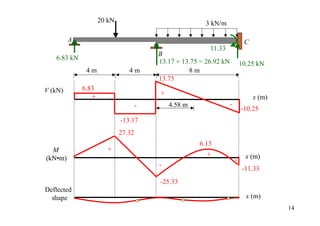
6.83 kN 13.17 kN 13.75 kN 10.25 kN 12

13. Note : Using the Slope 20 kN 3 kN/m
Deflection
2EI 3EI
20+10 16 16
A B C
4m 4m 8m
3(2 EI )
M BA = θ B − 30 − − − (1)
8
4(3EI )
M BC = θ B + 16 − − − (2)
8
MBA MBC
+ ΣMB = 0: -MBA - MBC = 0
B
(0.75 + 1.5)EIθB - 30 + 16 = 0
θB = 6.22/EI
MBA = -25.33 kN•m,
MBC = 25.33 kN•m
2(3EI )
M CB = θ B − 16 = −11.33 kN • m
8 13

14. 20 kN 3 kN/m
A C
11.33
B
6.83 kN
13.17 + 13.75 = 26.92 kN 10.25 kN
4m 4m 8m
13.75
6.83
V (kN)
+ + x (m)
- 4.58 m - -10.25
-13.17
27.32
6.13
M + +
(kN•m)
- - x (m)
-11.33
-25.33
Deflected
shape x (m)
14

15. Example 2
From the beam shown use the moment distribution method to:
(a) Determine all the reactions at supports, and also
(b) Draw its quantitative shear and bending moment diagrams,
and qualitative deflected shape.
10 kN 50 kN•m 5 kN/m
2EI 3EI 3EI
A B C D
4m 4m 8m 8m
15

16. 10 kN 50 kN•m 5 kN/m
2EI 15
26.67 26.67 40 3EI
A 0.5 B 0.5 C 0.5 D
4m 4m 8m 8m
K1 = 3(2EI)/8 K2 = 4(3EI)/8 K3 = 3(3EI)/8
K1/(K1+ K2) K2/(K1+ K2) K2/(K2+ K3) K3/(K2+ K3)
DF 1 0.333 0.667 0.571 0.428 1
Joint couple -16.65 -33.35
50 kN•m
CO=0 CO=0.5
50(.667) 50(.667)
50(.333)
50(.333) B
16

17. 10 kN 50 kN•m 5 kN/m
2EI 15
26.67 26.67 40 3EI
A 0.5 B 0.5 C 0.5 D
4m 4m 8m 8m
K1 = 3(2EI)/8 K2 = 4(3EI)/8 K3 = 3(3EI)/8
K1/(K1+ K2) K2/(K1+ K2) K2/(K2+ K3) K3/(K2+ K3)
DF 1 0.333 0.667 0.571 0.429 1
Joint couple -16.65 -33.35
CO -16.675
FEM -15 26.667 -26.667 40
Dist. -3.885 -7.782 1.905 1.437
CO 0.953 -3.891
Dist. -0.317 -0.636 2.218 1.673
CO 1.109 -0.318
Dist. -0.369 -0.740 0.181 0.137
Σ -36.22 -13.78 -43.28 43.25
17

18. 10 kN 50 kN•m 5 kN/m
2EI 36.22
13.78 43.25 43.25 3EI
A B C D
4m 4m 8m 8m
10 kN
40 kN
36.22 kN•m
A B 43.25 kN•m
C D
Ay = 0.47 kN ByL = 9.53 kN CyR = 25.41 kN Dy = 14.59 kN
40 kN
13.78 kN•m 43.25 kN•m
B C
ByR = 12.87 kN CyL= 27.13 kN
18

19. 10 kN 50 kN•m 5 kN/m
A D
2EI B C 3EI
0.47 kN 14.59 kN
9.53+12.87=22.4 kN 27.13+25.41=52.54 kN
4m 4m 8m 8m
12.87 25.41 2.92 m
V (kN) 0.47
x (m)
2.57 m
-9.53 -14.59
30.32 -27.13 21.29
13.78
M(kN•m) 1.88
x (m)
-36.22
-43.25
Deflected
x (m)
shape
19

20. Example 3
From the beam shown use the moment distribution method to:
(a) Determine all the reactions at supports, and also
(b) Draw its quantitative shear and bending moment diagrams, and
qualitative deflected shape.
2EI 40 kN 50 kN•m 10 kN/m 40 kN
A D
EI
B C
3m 3m 9m 3m
20

21. 120 kN•m 40 kN
2EI 40 kN 50 kN•m 10 kN/m
A D
30 30 101.25 EI
B C
0.5 0.5
3m 3m 9m 3m
K1 = 4(2EI)/6 K2 = 3(EI)/9
K1/(K1+ K2) K2/(K1+ K2)
DF 0 0.80 0.20 1
Joint couple 40 10 -120
CO 20 -60
FEM 30 -30 101.25
Dist.
Dist. -9 -2.25
CO -4.5
Σ 45.5 1 49 -120
21

22. 2EI 40 kN 50 kN•m 10 kN/m 40 kN
1
A D
49 120 120
45.5 EI
B C
3m 3m 9m 3m
40 kN
40 kN
45.5 kN•m 1 kN•m
A B 120 kN•m
C D
Ay = 27.75 kN ByL = 12.25 kN CyR = 40 kN
90 kN
49 kN•m 120 kN•m
B C
ByR = 37.11 kN CyL = 52.89 kN
22

23. 2EI 40 kN 50 kN•m 10 kN/m 40 kN
A D
EI
B C
27.75 kN
12.25+37.11 = 49.36 kN
52.89+40 = 92.89 kN
3m 3m 9m 3m
37.11 40
27.75
V (kN) + + +
- x (m)
-12.25 3.71 m -
37.75 -52.89
19.84
M(kN•m) + 1 + x (m)
- -
-
-45.5 -49
-120
Deflected x (m)
shape
23

24. Example 4
The support B of the beam shown (E = 200 GPa, I = 50x106 mm4 ) settles 10 mm.
Use the moment distribution method to:
(a) Determine all the reactions at supports, and also
(b) Draw its quantitative shear and bending moment diagrams,
and qualitative deflected shape.
20 kN 15 kN•m
12 kN•m 3 kN/m
2EI 3EI
A B C
4m 4m 8m
24

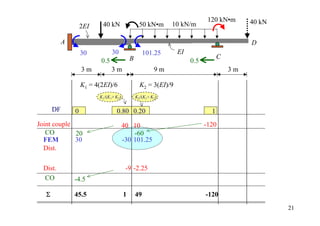
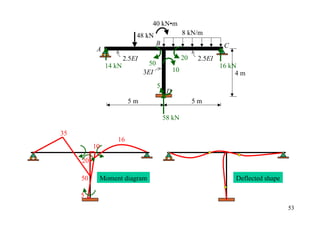
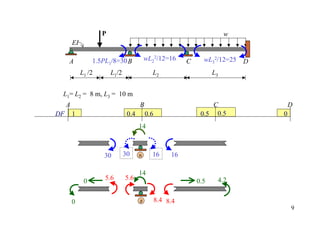
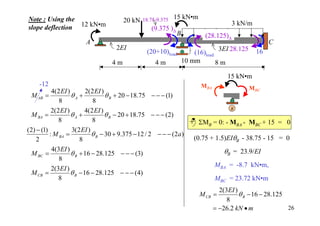
25. 20 kN 15 kN•m
12 kN•m 3 kN/m
B
A C
2EI 30 16 3EI
0.5 4 m 16
4m 10 mm 8 m
0.5
6(2 EI )∆ 6(2 EI )∆ 6(3EI ) ∆
A − = 9.375 6(3EI ) ∆ = 28.125
L 2
2L 2 = 28.125 L2
L2
∆ [FEM]∆ ∆
B B
6(2 EI )∆ C
L2 K1 = 3(2EI)/8 K2 = 4(3EI)/8
K1/(K1+ K2) K2/(K1+ K2)
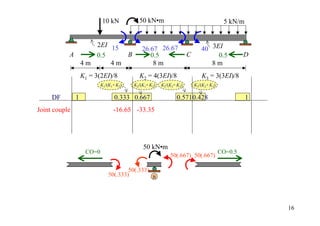
DF 1 0.333 0.667 0
Joint couple -12 5 10
CO -6 5
[FEM]load -30 16 -16
[FEM]∆ 9.375 -28.125 -28.125
Dist. 12.90 25.85
CO 12.92
Σ -12 -8.72 23.72 -26.20 25

26. Note : Using the 20 kN 18.75-9.375 15 kN•m
3 kN/m
slope deflection 12 kN•m (9.375 )∆
B (28.125)∆
A C
2EI 3EI 28.125
(20+10)load (16)load 16
4m 4m 10 mm 8m
15 kN•m
-12 MBA MBC
4(2 EI ) 2(2 EI )
M AB = θA + θ B + 20 − 18.75 − − − (1)
8 8
B
2(2 EI ) 4(2 EI )
M BA = θA + θ B − 20 + 18.75 − − − (2)
8 8 + ΣMB = 0: - MBA - MBC + 15 = 0
( 2) − (1) 3(2 EI )
: M BA = θ B − 30 + 9.375 − 12 / 2 − − − (2a)
2 8 (0.75 + 1.5)EIθB - 38.75 - 15 = 0
4(3EI ) θB = 23.9/EI
M BC = θ B + 16 − 28.125 − − − (3)
8
MBA = -8.7 kN•m,
2(3EI )
M CB = θ B − 16 − 28.125 − − − (4)
8 MBC = 23.72 kN•m
2(3EI )
M CB = θ B − 16 − 28.125
8
= −26.2 kN • m 26

27. 20 kN 15 kN•m
12 kN•m 3 kN/m
2EI 8.725 23.7253EI 26.205
A B C
4m 4m 8m
20 kN 24 kN
12 kN•m
8.725 kN•m 26.205 kN•m
A B B C
23.725 kN•m
Ay = 7.41 kN ByL = 12.59 kN ByR = 11.69 kN Cy = 12.31 kN
27

28. 20 kN 15 kN•m
12 kN•m 3 kN/m
A C
2EI B 3EI 26.205
7.41 kN
12.59+11.69 = 24.28 kN 12.31 kN
4m 4m 8m
7.41 11.69
V (kN)
+ + x (m)
- 3.9 m - -12.31
-12.59
41.64
12
+
M
(kN•m) x (m)
-8.725 - -0.93 -
-23.725 -26.205
Deflected 10 mm θB = 23.9/EI
shape x (m)
28

29. Example 5
For the beam shown, support A settles 10 mm downward, use the moment
distribution method to
(a)Determine all the reactions at supports
(b)Draw its quantitative shear, bending moment diagrams, and qualitative
deflected shape.
Take E= 200 GPa, I = 50(106) mm4.
12 kN•m
6 kN/m
B
A
2EI C 1.5EI 10 mm
3m 3m
29

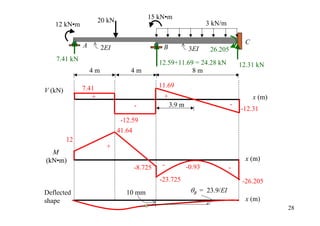
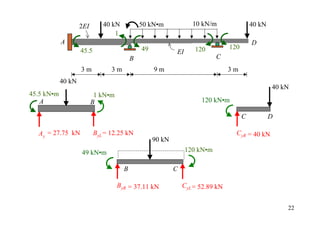
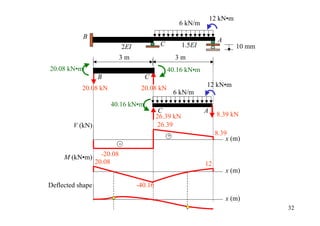
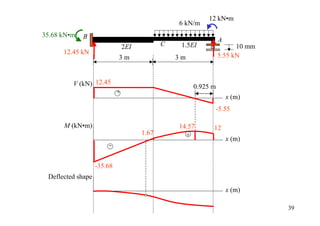
30. 12 kN•m
4.5+(4.5/2) 6 kN/m
= 6.75
B
A
4.5 10 mm
2EI C 1.5EI
3m 0.5 3 m 0.5
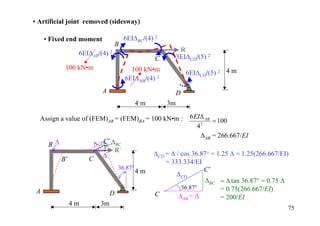
100-(100/2) = 50 6(1.5 × 200 × 50)(0.01)
0.01 m
C 32
MF∆
A = 100 kN • m
K1 = 4(2EI)/3 K2 = 3(1.5EI)/3
K1/(K1+ K2) K2/(K1+ K2)
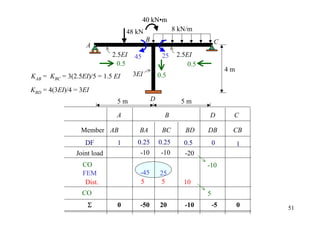
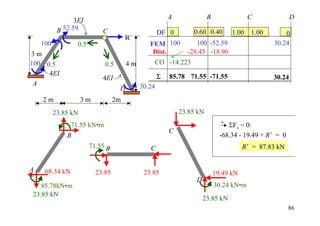
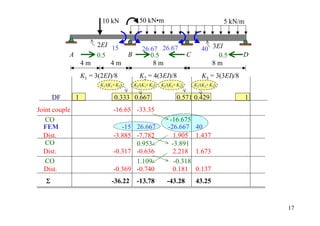
DF 0 0.64 0.36 1
Joint couple 12
CO 6
[FEM]load 6.75
[FEM]∆ 50
Dist. -40.16 -22.59
CO -20.08
Σ -20.08 -40.16 40.16 12 30

31. 12 kN•m
6 kN/m
B
A
2EI C 1.5EI
3m 3m
ΣΜ -20.08 -10.16 40.16 12
20.08 kN•m 40.16 kN•m
B C
40.16 + 20.08
20.08 kN = 20.08 kN
3
18 kN
12 kN•m
6 kN/m
40.16 kN•m
C A
26.39 kN 8.39 kN
31

32. 12 kN•m
6 kN/m
B
A
2EI C 1.5EI 10 mm
3m 3m
20.08 kN•m 40.16 kN•m
B C
20.08 kN 20.08 kN 12 kN•m
6 kN/m
40.16 kN•m
C A
26.39 kN 8.39 kN
V (kN) 26.39
+ 8.39
x (m)
-
M (kN•m) -20.08
20.08 12
x (m)
Deflected shape -40.16
x (m)
32

33. Example 6
For the beam shown, support A settles 10 mm downward, use the moment
distribution method to
(a)Determine all the reactions at supports
(b)Draw its quantitative shear, bending moment diagrams, and qualitative
deflected shape.
Take E= 200 GPa, I = 50(106) mm4.
12 kN•m
6 kN/m
B
A
2EI C 1.5EI 10 mm
3m 3m
33

34. • Overview 12 kN•m
6 kN/m
B
A
C 10 mm
2EI 1.5EI
3m 3m
12 kN•m
6 kN/m
B
A
10 mm
C
R
∆
B ×C
A
R´
R + R ' C = 0 − − − (1*)
34

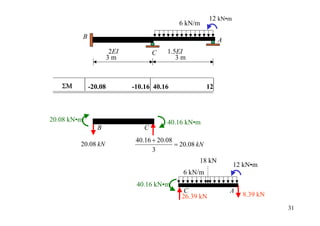
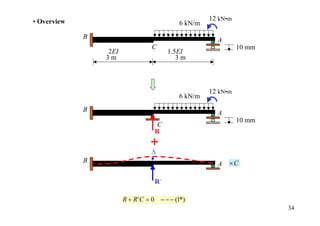
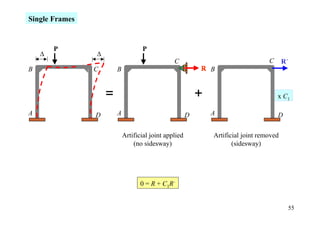
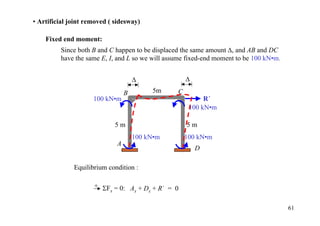
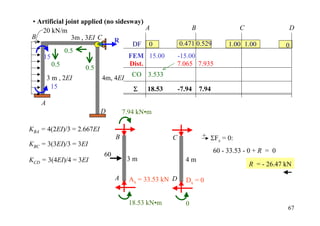
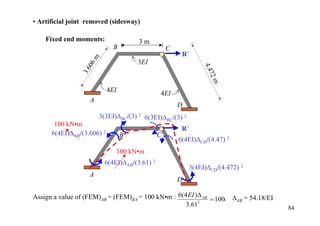
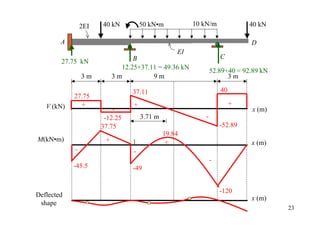
35. • Artificial joint applied 12 kN•m
4.5+(4.5/2) 6 kN/m
= 6.75
B
A
4.5 10 mm
2EI C 1.5EI
3m 0.5 3 m 0.5
100-(100/2) = 50 6(1.5 × 200 × 50)(0.01)
0.01 m
C 32
MF∆
A = 100 kN • m
K1 = 4(2EI)/3 K2 = 3(1.5EI)/3
K1/(K1+ K2) K2/(K1+ K2)
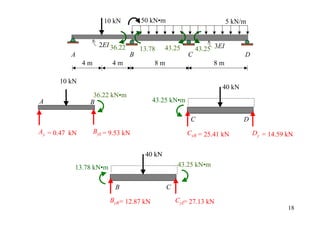
DF 0 0.64 0.36 1
Joint couple 12
CO 6
[FEM]load 6.75
[FEM]∆ 50
Dist. -40.16 -22.59
CO -20.08
Σ -20.08 -40.16 40.16 12 35

36. 12 kN•m
6 kN/m
B
A
2EI C 1.5EI
3m 3m
ΣΜ -20.08 -40.16 40.16 12
20.08 kN•m 40.16 kN•m
B C
40.16 + 20.08 18 kN
20.08 kN = 20.08 kN 12 kN•m
3 6 kN/m
40.16 kN•m
C A
26.39 kN 8.39 kN
40.16 kN•m
40.16 kN•m
20.08 C 26.39 kN + ↑ ΣFy = 0 : − 20.08 − 26.39 + R = 0
R
R = 46.47 kN 36

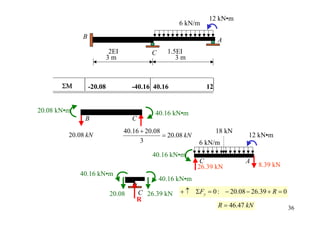
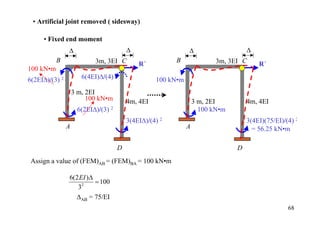
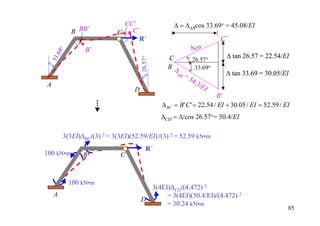
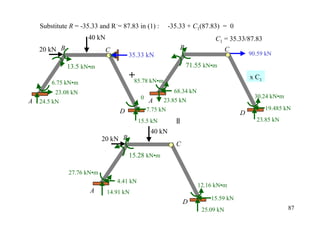
37. • Artificial joint removed
∆
B
A
C
2EI 0.5 1.5EI 0.5
3m R´ 3m
C C
75
B ∆ ∆ 6(1.5EI )( )
100 EI = 75
75-(75/2) A 32
6(2 EI ) ∆ C 75
= 100 → ∆ = = 37.5
32 EI
DF 0 0.64 0.36 1
[FEM]∆ -100 -100 +37.5
Dist. 40 22.5
CO 20
Σ -80 -60 60
80 kN•m 60 kN•m 60 kN•m
B C C A
46.67 kN 46.67 kN 20 kN 20 kN
C
46.67 20 kN + ↑ ΣFy = 0 : R' = 66.67 kN 37
R´

38. • Solve equation
Substitute R = 46.47 kN and R ' = 66.67 kN in (1*)
46.47 + 66.67C = 0
C = −0.6970
12 kN•m
6 kN/m
B
20.08 kN•m A
10 mm
20.08 kN C
R = 46.47 kN 8.39 kN
∆
B
80 kN•m A × C = −0.6970
46.67 kN 20 kN
R´ = 66.67 kN
12 kN•m
6 kN/m
35.68 kN•m B
A
2EI C 1.5EI
12.45 kN 5.55 kN 38

39. 12 kN•m
6 kN/m
35.68 kN•m B
A
2EI C 1.5EI 10 mm
12.45 kN 5.55 kN
3m 3m
V (kN) 12.45 0.925 m
+
x (m)
-5.55
M (kN•m) 14.57 12
1.67 +
x (m)
-
-35.68
Deflected shape
x (m)
39

40. Symmetric Beam
• Symmetric Beam and Loading
P P
θ θ
A B C D
L´ L L´
real beam
V´B L L V´C
M L
2 2 + ΣMC´ = 0: − VB ' ( L ) + ( L)( ) = 0
EI 2
B´ C´
ML
M VB ' = θ =
M 2 EI
L EI
EI
2 EI
conjugate beam M= θ
L
The stiffness factor for the center span is, therefore,
2 EI
K=
L
40

41. • Symmetric Beam with Antisymmetric Loading
P
θ
A D
B θ C
P
L´ L L´
real beam
1 M L M 1 M L 2L
( )( ) + ΣMC´ = 0: − VB ' ( L) + ( )( )( ) = 0
2 EI 2 EI 2 EI 2 3
V´B 2 ML
L VB ' = θ =
B´ 3 6 EI
C´
6 EI
1 M L V´C M= θ
M ( )( ) L
2 EI 2
EI The stiffness factor for the center span is, therefore,
conjugate beam
6 EI
K=
L 41

42. Example 5a
Determine all the reactions at supports for the beam below. EI is constant.
15 kN/m
A D
B C
4m 6m 4m
42

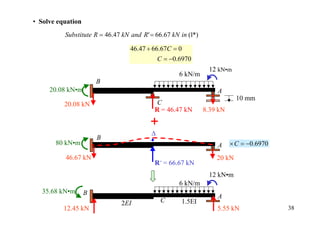
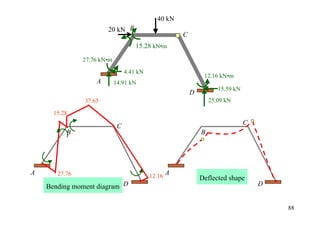
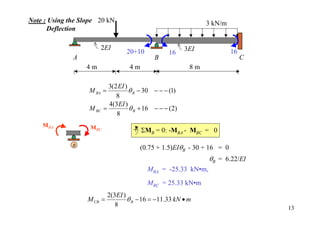
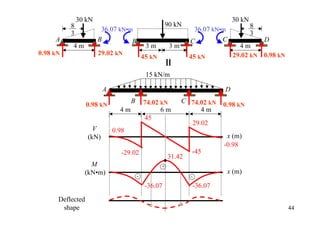
43. 15 kN/m
A D
wL2/15 = 16 B wL2/12 = 45 C wL2/15 = 16
4m 6m 4m
3EI 3EI 2 EI 2 EI
K ( AB ) = = , K ( BC ) = =
L 4 L 6
K ( AB ) K ( AB ) (3EI / 4)
( DF ) AB = = 1,( DF ) BA = = = 0.692,
K ( AB ) K ( AB ) + K ( BC ) (3EI / 4) + ( 2 EI / 6)
K ( BC ) (2 EI / 6)
( DF ) BC = = = 0.308
K ( AB ) + K ( BC ) (3EI / 4) + (2 EI / 6)
DF 1.0 0.692 0.308
[FEM]load 0 -16 +45
Dist. -20.07 -8.93
ΣΜ -36.07 +36.07
30 kN 30 kN
8 90 kN 8
36.07 kN•m 36.07 kN•m
3 3
A B B C C D
4m 3m 3m 4m
0.98 kN 29.02 kN 29.02 kN 0.98 kN 43
45 kN 45 kN

44. 30 kN 30 kN
8 90 kN 8
36.07 kN•m 36.07 kN•m
3 3
A B B C C D
4m 3m 3m 4m
0.98 kN 29.02 kN 29.02 kN 0.98 kN
45 kN 45 kN
15 kN/m
A D
B 74.02 kN C 74.02 kN
0.98 kN 0.98 kN
4m 6m 4m
45
29.02
V 0.98
(kN) x (m)
-0.98
-29.02 -45
31.42
M +
(kN•m) x (m)
- -
-36.07 -36.07
Deflected
shape 44

45. Example 5b
Determine all the reactions at supports for the beam below. EI is constant.
15 kN/m
A C D
B
15 kN/m
4m 3m 3m 4m
45

46. Fixed End Moment 15 kN/m
A C D
wL2/15 = 16 B 11wL2/192 5wL2/192
= 30.938 = 14.063
5wL2/192 11wL2/192
= 14.063 = 30.938 wL2/15 = 16
A C D
B
15 kN/m
15 kN/m
16.875 16
A C D
16 B 16.875
15 kN/m
46

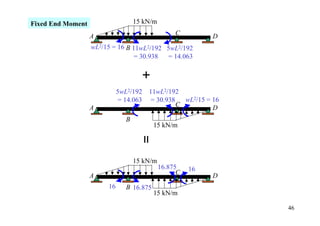
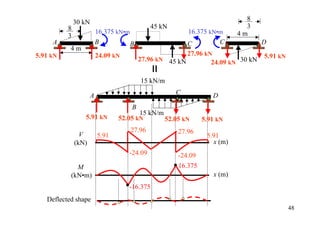
47. 15 kN/m
16.875 16
A C D
16 B 16.875
15 kN/m
4m 3m 3m 4m
3EI 3EI 6 EI 6 EI
K ( AB ) = = = 0.75EI , K ( BC ) = = = EI
L 4 L 6
0.75 1
( DF ) AB = 1, ( DF ) BA = = 0.429, ( DF ) BC = = 0.571
0.75 + 1 0.75 + 1
DF 1.0 0.429 0.571
[FEM]load 0 -16 16.875
Dist. -0.375 -0.50
ΣΜ -16.375 16.375
8
30 kN
8 45 kN 3
16.375 kN•m 16.375 kN•m 4m
3
A B B C C D
4m
5.91 kN 24.09 kN 27.96 kN 5.91 kN
27.96 kN 45 kN 24.09 kN 30 kN 47

48. 8
30 kN
8 45 kN 3
16.375 kN•m 16.375 kN•m 4m
3
A B B C C D
4m
5.91 kN 24.09 kN 27.96 kN 5.91 kN
27.96 kN 45 kN 24.09 kN 30 kN
15 kN/m
A C D
B
15 kN/m
5.91 kN 52.05 kN 52.05 kN 5.91 kN
27.96 27.96
V 5.91 5.91
(kN) x (m)
-24.09 -24.09
M 16.375
(kN•m) x (m)
-16.375
Deflected shape
48

49. Moment Distribution Frames: No Sidesway
49

50. Example 6
From the frame shown use the moment distribution method to:
(a) Determine all the reactions at supports
(b) Draw its quantitative shear and bending moment diagrams,
and qualitative deflected shape.
40 kN•m
48 kN 8 kN/m
B C
A
2.5EI 2.5EI
4m
3EI
5m D 5m
50

51. 40 kN•m
48 kN 8 kN/m
B C
A
2.5EI 45 25 2.5EI
0.5 0.5
4m
KAB = KBC = 3(2.5EI)/5 = 1.5 EI 3EI 0.5
KBD = 4(3EI)/4 = 3EI
5m D 5m
A B D C
Member AB BA BC BD DB CB
DF 1 0.25 0.25 0.5 0 1
Joint load -10 -10 -20
CO -10
FEM -45 25
Dist. 5 5 10
CO 5
Σ 0 -50 20 -10 -5 0 51

52. 40 kN•m
48 kN 8 kN/m
B C
A
20
2.5EI 50 2.5EI
14 kN 10 16 kN
3EI
5 Member AB BA BC BD DB CB
D Σ 0 -50 20 -10 -5 0
40 kN•m
58 kN 34 24 3.75
50 20
48 kN 3.75 40 kN
A B 0 50 kN•m 58
10 B C 3.75
58 20 3.75
14 kN 34 kN 10 kN•m 16 kN
24 kN
3.75 kN
5
3.75 kN
58
52

53. 40 kN•m
48 kN 8 kN/m
B C
A
2.5EI 20 2.5EI
14 kN 50 16 kN
3EI 10 4m
5
D
5m 5m
58 kN
35
16
10
20
50 Moment diagram Deflected shape
5
53

54. Moment Distribution for Frames: Sidesway
54

55. Single Frames
P P
∆ ∆
C C R´
B C B R B
x C1
A D A D A D
Artificial joint applied Artificial joint removed
(no sidesway) (sidesway)
0 = R + C1R´
55

56. Multistory Frames ∆2 P3
P2
P4
P1 ∆1
P3
∆´´ ∆´´
P2 R2´´
R2 R2´
∆´ ∆´
P4
x C1 x C2
P1 R1´
R1 R1´´
0 =R2 + C1R2´ + C2R2´´
0 =R1 + C1R1´ + C2R2´´
56

57. Example 7
From the frame shown use the moment distribution method to:
(a) Determine all the reactions at supports, and also
(b) Draw its quantitative shear and bending moment diagrams, and
qualitative deflected shape.
EI is constant.
16 kN
1m 4m
B C
5m
A D
57

58. • Overview
16 kN 16 kN
1m 4m C C R´
B C B R B
5m 5m = + x C1
A D A D A D
artificial joint applied artificial joint removed
(no sidesway) ( sidesway)
R + C1R´ = 0 ---------(1)
58

59. • Artificial joint applied (no sidesway)
Fixed end moment:
16 kN
b=1m a=4m C
B R
Pa2b/L2 Pb2a/L2
= 10.24 = 2.56
A D
Equilibrium condition :
+ ΣF = 0: A + D + R = 0
x x x
59

60. 16 kN
1m 4m C
R A B C D
B
0.5 DF 0 0.50 0.50 0.50 0.50
10.24 2.56 0
FEM 10.24 -2.56
5m 5m Dist. -5.12 -5.12 1.28 1.28
0.5 0.5
CO -2.56 0.64 -2.56 0.64
A D Dist. -0.32 -0.32 1.28 1.28
CO -0.16 0.64 -0.16 0.64
5.78 kN•m Dist. -0.32 -0.32 0.08 0.08
2.72 kN•m
CO -0.16 0.04 -0.16 0.04
Dist. -0.02 -0.02 0.08 0.08
B C Σ -2.88 -5.78 5.78 -2.72 2.72 1.32
5m 5m Equilibrium condition :
+ ΣF = 0: 1.73 - 0.81 + R = 0
x
A Ax = 1.73 kN D
Dx = 0.81 kN R = - 0.92 kN
2.88 kN•m 1.32 kN•m
60

61. • Artificial joint removed ( sidesway)
Fixed end moment:
Since both B and C happen to be displaced the same amount ∆, and AB and DC
have the same E, I, and L so we will assume fixed-end moment to be 100 kN•m.
∆ ∆
B 5m C
100 kN•m R´
100 kN•m
5m 5m
100 kN•m 100 kN•m
A
D
Equilibrium condition :
+ ΣF = 0: A + D + R´ = 0
x x x
61

62. ∆ ∆
B 5m C
R´ A B C D
0.5 0.50 0.50
100 kN•m 100 kN•m DF 0 0.50 0.50 0
FEM 100 100 100 100
5m 5m Dist. -50 -50 -50 -50
0.5 0.5
100 kN•m 100 kN•m CO -25.0 -25.0 -25.0 -25.0
A Dist. 12.5 12.5 12.5 12.5
D
CO 6.5 6.5 6.5 6.5
Dist. -3.125 -3.125 -3.125 -3.125
60 kN•m 60 kN•m CO -1.56 -1.56 -1.56 -1.56
Dist. 0.78 0.78 0.78 0.78
CO 0.39 0.39 0.39 0.39
B C
Dist. -0.195 -0.195 -0.195 -0.195
Σ 80 60 -60 -60 60 80
5m 5m
Equilibrium condition: + ΣFx = 0:
A Ax = 28 kN D
Dx = 28 kN -28 - 28 + R´ = 0
80 kN•m 80 kN•m R´ = 56 kN
62

63. Substitute R = -0.92 and R´= 56 in (1) :
R + C1R´ = 0
-0.92 + C1(56) = 0
0.92
C1 =
56
16 kN 16 kN
B C C R´ 1m 4m C
R B B
5.78 2.72 60 60 4.79 3.71
2.72 60 60 3.71
5.78 4.79
+ x C1 = 5m 5m
2.88 80 80 1.57 2.63
1.32
1.73 kN 0.81 28 28 1.27 kN
A D A D A D 1.27
63

64. 8.22
16 kN
3.71
1m 4m C
B 4.79
4.79 3.71 3.71
4.79
4.79 3.71
5m 5m
1.57 2.63
1.27 kN 1.27 kN 1.57 2.63
A D 2.99 kN Bending moment
13.01 kN diagram (kN•m)
∆ ∆
Deflected shape 64

65. Example 8
From the frame shown use the moment distribution method to:
(a) Determine all the reactions at supports, and also
(b) Draw its quantitative shear and bending moment diagrams, and
qualitative deflected shape.
20 kN/m 3m
B pin
C
3EI
3m 2EI
4EI 4m
A
D
65

66. • Overview
20 kN/m
B 3m, 3EI B C B C
C
R R´
3 m , 2EI
4m , 4EI
= + x C1
A A A
D D D
artificial joint applied artificial joint removed
(no sidesway) (sidesway)
R + C1R´ = 0 ----------(1)
66

67. • Artificial joint applied (no sidesway)
20 kN/m A B C D
B 3m , 3EI C R 0.471 0.529
DF 0 1.00 1.00 0
0.5
15 FEM 15.00 -15.00
0.5 Dist. 7.065 7.935
0.5
CO 3.533
3 m , 2EI 4m, 4EI
15 Σ 18.53 -7.94 7.94
A
D 7.94 kN•m
KBA = 4(2EI)/3 = 2.667EI
B C + ΣF = 0:
x
KBC = 3(3EI)/3 = 3EI
60 - 33.53 - 0 + R = 0
60
KCD = 3(4EI)/4 = 3EI 3m 4m
R = - 26.47 kN
A Ax = 33.53 kN D Dx = 0
18.53 kN•m 0
67

68. • Artificial joint removed ( sidesway)
• Fixed end moment
∆ ∆ ∆ ∆
B 3m, 3EI C B 3m, 3EI C
R´ R´
100 kN•m
6(2EI∆)/(3) 2 6(4EI)∆/(4) 2 100 kN•m
3 m, 2EI
100 kN•m 4m, 4EI 3 m, 2EI 4m, 4EI
6(2EI∆)/(3) 2 100 kN•m
3(4EI∆)/(4) 2 3(4EI)(75/EI)/(4) 2
A A = 56.25 kN•m
D D
Assign a value of (FEM)AB = (FEM)BA = 100 kN•m
6(2 EI ) ∆
2
= 100
3
∆AB = 75/EI
68

69. ∆ ∆
A B C D
B 3m C R´
0.5 DF 0 0.471 0.529 1.00 1.00 0
100
FEM 100 100 56.25
0.5
Dist. -47.1 -52.9 0
0.5
3m 4m CO -28.55
100
Σ 76.45 52.9 -52.9 56.25
56.25
A
D
52.9. kN•m
+ ΣF = 0:
C x
B -43.12 - 14.06 + R´ = 0
3m 4m R´ = 57.18 kN
A Ax = 43.12kN
D 14.06 kN
76.45 kN•m
56.25 kN•m 69

70. Substitute R = -26.37 and R´= 57.18 in (1) :
R + C1R´ = 0
-26.47 + C1(57.18) = 0
26.47
C1 =
57.18
20 kN/m
B B 52.9 kN•m B
C C 3m
R C
7.94 kN•m R´ 16.55 kN•m
7.94 kN•m 52.9
= 3m
+ 76.45 kN•m
x C1 4m
18.53 kN•m 53.92 kN•m
33.53 kN 43.12 kN 53.49 kN
A A 56.25
0 A 26.04 kN•m
5.52 kN kN
6.51
0
D D 14.06 D
5.52 kN
70

71. 20 kN/m
16.55
B 3m 16.55
C B C
16.55 kN•m
3m
53.92 kN•m 4m
53.92
53.49 kN
A 26.04 kN•m A
5.52 kN kN
6.51 26.04
Moment diagram
∆ ∆ D
D
5.52 kN
B C
A
Deflected shape
71
D

72. Example 8
From the frame shown use the moment distribution method to:
(a) Determine all the reactions at supports, and also
(b) Draw its quantitative shear and bending moment diagrams,
and qualitative deflected shape.
EI is constant.
10 kN B
C
4m
A D
4m 3m
72

73. • Overview
10 kN B
C
4m
A D
4m 3m
R + C1R´ = 0 ---------(1)
=
10 kN B C B C
R R´
+ x C1
A D A D
artificial joint applied artificial joint removed
(no sidesway) (sidesway)
73

74. • Artificial joint applied (no sidesway)
10 kN B C
R
0 0
A D
Equilibrium condition : + ΣF = 0:
x
10 + R = 0
R = - 10 kN
74

75. • Artificial joint removed (sidesway)
• Fixed end moment 6EI∆BC/(4) 2
B
R´
6EI∆AB/(4) 2
C 3EI∆CD/(5) 2
100 kN•m 100 kN•m
6EI∆CD/(5) 2 4 m
6EI∆AB/(4) 2
A D
4m 3m
Assign a value of (FEM)AB = (FEM)BA = 100 kN•m : 6 EI∆ AB = 100
42
∆AB = 266.667/EI
∆ CD ∆BC
B∆ C´
R´
∆ ∆CD = ∆ / cos 36.87° = 1.25 ∆ = 1.25(266.667/EI)
B´ C = 333.334/EI
36.87° C´
4m ∆CD
∆BC = ∆ tan 36.87° = 0.75 ∆
36.87° = 0.75(266.667/EI)
A D C ∆AB = ∆ = 200/EI
4m 3m
75

76. ∆BC= 200/EI, ∆CD = 333.334/EI
6EI∆BC/(4) 2 = 6(200)/42 = 75 kN•m
B
R´
100 kN•m
C 3EI∆CD/(5) 2 = 3(333.334)/52 = 40 kN•m
100 kN•m
A D
Equilibrium condition :
+ ΣF = 0: A + D + R´ = 0
x x x
76

77. 75 A B C D
B 75
R´ DF 0 0.50 0.50 0.625 0.375 1
0.5 C
100 FEM 100 100 -75 -75 40
40
4 m Dist. -12.5 -12.5 21.875 13.125
0.5 0.5
100 CO -6.25 10.938 -6.25
A D Dist. -5.469 -5.469 3.906 2.344
4m 3m CO -2.735 1.953 -2.735
Dist. -0.977 -0.977 1.709 1.026
KBA = 4EI/4 = EI, KBC = 4EI/4 = EI,
KCD = 3EI/5 = 0.6EI Σ 91.02 81.05 -81.05 -56.48 56.48
34.38 kN 34.38 kN
81.05 81.05 B C 56.48
B 56.48 C
34.38 kN 34.38 kN
+ ΣF = 0: 39.91 kN
A 43.02 kN x D
91.02 -43.02 - 39.91 + R´ = 0
34.38 kN R´ = 82.93 kN 34.38 kN
77

78. Substitute R = -10 kN and R´= 82.93 kN in (1) : -10 + C1(82.93) = 0
R + C1R´ = 0 ---------(1) C1 = 10/82.93
81.05
10 kN B C B C
R R´
81.05 56.48
x C1= 10/82.93
+ 56.48
0 0 91.02 39.91 kN
A 0 D A 43.02 kN D
0
=
34.38 kN
0 34.38 kN
9.77
10 kN B
C
9.77 6.81
6.81 4m
10.98 4.81 kN
A 5.19 kN
D
4.15 kN 4.15 kN
4m 3m
78

79. 9.77
10 kN B
C
9.77 6.81
6.81 4m
10.98
A 5.19 kN 4.81 kN
D
4.15 kN 4.15 kN
4m 3m
9.77
B B
9.77 C C
6.81
A 10.98 A
D D
Bending moment diagram Deflected shape
(kN•m)
79

80. Example 9
From the frame shown use the moment distribution method to:
(a) Determine all the reactions at supports, and also
(b) Draw its quantitative shear and bending moment diagrams,and
qualitative deflected shape.
EI is constant.
40 kN
20 kN B
C
3EI
3m
4EI
4EI 4m
A
D
2m 3m 2m
80

81. 40 kN
• Overview
20 kN B
C
3EI
3m
4EI
4EI 4m
A
D
2m 3m 2m
R + C1R´ = 0 ----------(1)
40 kN
=
20 kN B C B C
R R´
+ x C1
artificial joint applied artificial joint removed
(no sidesway) (no sidesway)
A A
D D
2m 3m 2m 2m 3m 2m
81

82. • Artificial joint applied (no sidesway)
Fixed end moments:
40 kN
PL/8 = 15
B C
20 kN R
15+(15/2)
= 22.5 kN•m
A
D
2m 3m 2m
Equilibrium condition :
+ ΣF = 0: A + D + R = 0
x x x
82

83. A B C D
40 kN
20 kN B C DF 0 0.60 0.40 1.00 1.00 0
R
22.5 FEM 22.5
15
0.5 Dist. -13.5 -9.0
0.5 0.5 CO -6.75
Σ -6.75 -13.5 13.5
A
D
2m 3m 2m KBA = 4(4EI)/3.6 = 4.444EI, KBC = 3(3EI)/3 = 3EI,
24.5 kN 15.5 kN
13.5 kN•m
C + ΣF = 0:
B x
40 kN 23.08 + 20 -7.75 + R´ = 0
13.5 B C R´ = - 35.33 kN
A 7.75 kN
23.08 kN
24.5 kN 15.5 kN D
6.75 kN•m 0
24.5 kN 15.5 kN
83

84. • Artificial joint removed (sidesway)
Fixed end moments: 3m
B C
R´
m
3EI
06
4. 4
3.6
72
m
4EI
4EI
A
D
3(3EI)∆BC/(3) 2 6(3EI)∆BC/(3) 2
100 kN•m
R´
6(4EI)∆AB/(3.606) 2 B C
6(4EI)∆CD/(4.47) 2
100 kN•m
6(4EI)∆AB/(3.61) 2
3(4EI)∆CD/(4.472) 2
A
D
Assign a value of (FEM)AB = (FEM)BA = 100 kN•m : 6(4 EI ) ∆ AB = 100, ∆AB = 54.18/EI
3.612 84

85. CC´ ∆ = ∆ABcos 33.69° = 45.08/EI
B BB´ C C´
R´ C´
B´ ∆ CD
.69 o C ∆ tan 26.57 = 22.54/EI
26.57°
26.57°
33
B∆ 33.69o
AB
=5 ∆ tan 33.69 = 30.05/EI
4.3
A /E I
D
B´
∆ BC = B' C ' = 22.54 / EI + 30.05 / EI = 52.59 / EI
∆CD = ∆/cos 26.57°= 50.4/EI
3(3EI)∆BC/(3) 2 = 3(3EI)(52.59/EI) /(3) 2 = 52.59 kN•m
R´
100 kN•m B C
100 kN•m
3(4EI)∆CD/(4.472) 2
A = 3(4EI)(50.4/EI)/(4.472) 2
D
= 30.24 kN•m
85

86. A B C D
3EI
B 52.59 C DF 0 0.60 0.40 1.00 1.00 0
R´
100 0.5 FEM 100 100 -52.59 30.24
3m Dist. -28.45 -18.96
100 0.5 0.5 4m CO -14.223
4EI Σ 85.78 71.55 -71.55
4EI 30.24
A 30.24
D
2m 3m 2m
23.85 kN 23.85 kN
71.55 kN•m + ΣF = 0:
x
C
B -68.34 - 19.49 + R´ = 0
71.55 B C R´ = 87.83 kN
A 68.34 kN 23.85 23.85 19.49 kN
D
85.78kN•m 30.24 kN•m
23.85 kN
23.85 kN
86

87. Substitute R = -35.33 and R´= 87.83 in (1) : -35.33 + C1(87.83) = 0
40 kN C1 = 35.33/87.83
20 kN B C B C
35.33 kN 90.59 kN
13.5 kN•m 71.55 kN•m
+85.78 kN•m x C1
6.75 kN•m
23.08 kN 68.34 kN
0 30.24 kN•m
A 24.5 kN A 23.85 kN
7.75 kN 19.485 kN
D D
15.5 kN 23.85 kN
=
40 kN
20 kN B
C
15.28 kN•m
27.76 kN•m
4.41 kN
12.16 kN•m
A 14.91 kN
15.59 kN
D
25.09 kN 87

88. 40 kN
20 kN B
C
15.28 kN•m
27.76 kN•m
4.41 kN
12.16 kN•m
A 14.91 kN
15.59 kN
D
37.65 25.09 kN
15.28
C C
B B
A 27.76 A
12.16 Deflected shape
Bending moment diagram D D
88