Downloaded 49 times
Uploaded byRiya Gupta
7 8.math projection (2)
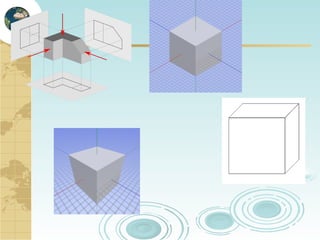
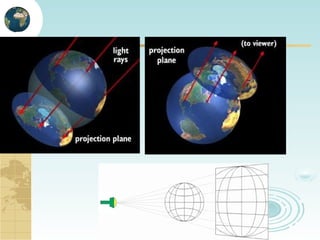
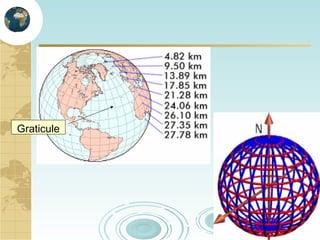
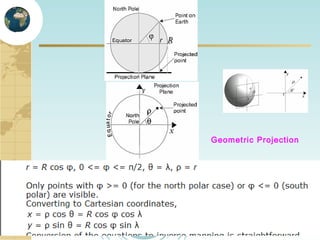
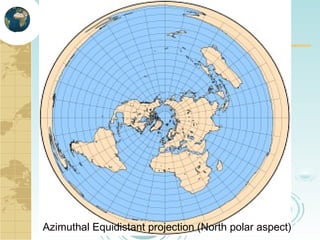
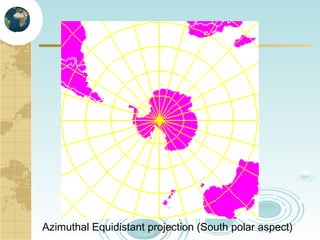
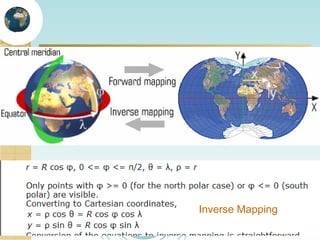
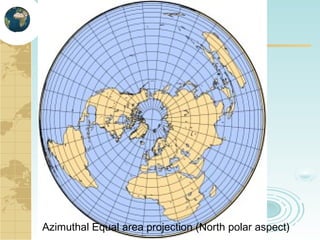
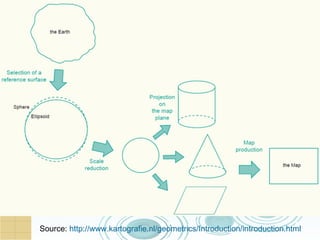
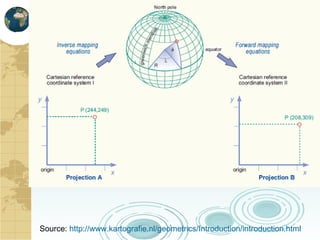
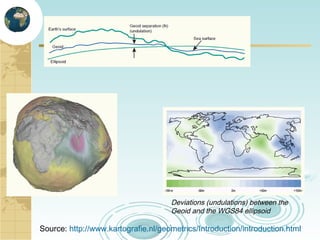
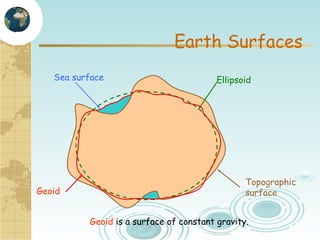
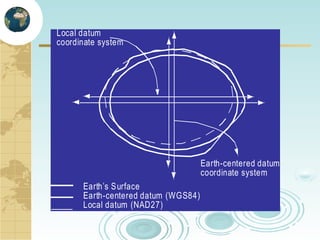
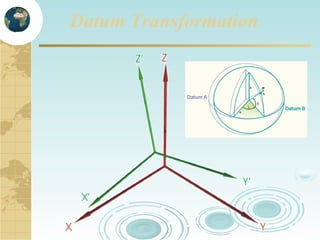
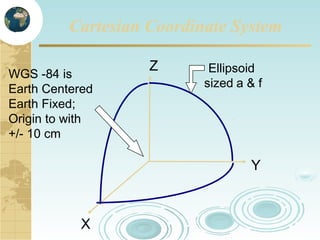
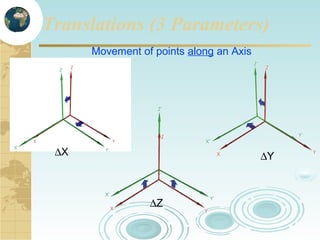
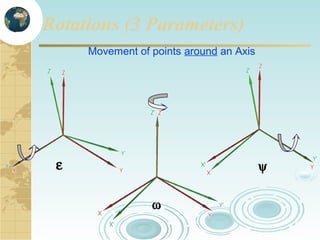
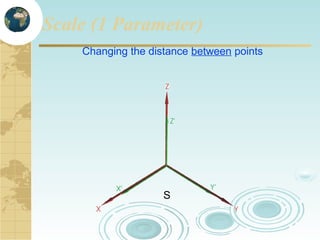
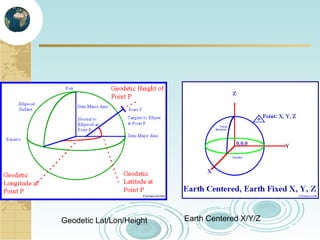
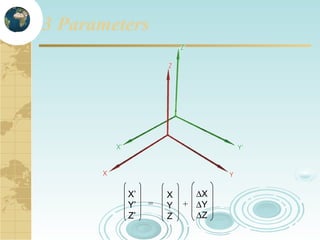
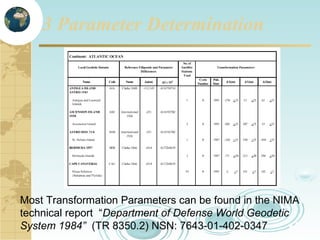
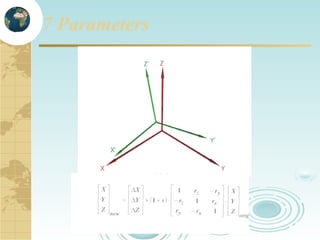
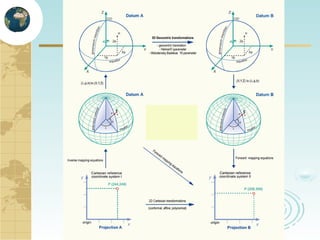
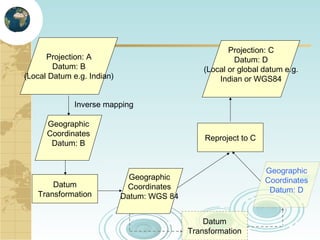
This document discusses key concepts related to map projections and datums. It defines projections as mathematical transformations that take 3D objects on the earth's surface and project them onto a 2D surface, like a map, with minimal distortion. It discusses different types of projections, important properties to preserve like distances and shapes, and how different projections preserve certain properties better in specific regions. The document also defines datums as reference frames that define latitude/longitude and how local datums need to be transformed to global datums like WGS84. It explains factors like the earth not being a perfect sphere and irregular terrain that necessitate datums and datum transformations.
More Related Content
Similar to 7 8.math projection (2)
7 8.math projection (2)
- 1.
- 2. To locate GeographicPosition A model (3D) of the earth surface Spheroid How the 3D model is related to the shape of the earth? Datum A model to translate the 3D points on a 2D surface with minimal distortion Projection A coordinate system to measure the points 3D or 2D
- 3. What is aProjection? Mathematical transformation of 3D objects in a 2D space with minimal distortion This two-dimensional surface would be the basis for your map.
- 4. Engineering Drawing Types ofProjections Orthographic Isometric Perspective Oblique
- 6. For any map,the most important parameters of accuracy can be expressed as: can distances be accurately measured? are directions preserved? are shapes preserved? are area ratios preserved? which regions suffer the most, and which kind of, distortion?
- 7. Although all propertiescannot be preserved, a reasonably small spherical patch can be approximated by a flat sheet with acceptable distortion In most projections, at least one specific region (usually the center of the map) suffers little or no distortion. If the represented region is small enough , the projection choice may be of little importance.
- 8. Geometric Projection geometric interpretationas light rays projected from a source intercept the Earth and, according to laws of perspective, "draw" its features on a surface (Plane, cylinder, or cone) Algorithmic Projection are described purely by mathematical formulae • E.g. equal-distant, equal area etc.,
- 10.
- 11. Graticules as aguide for distortion along any meridian, the distance on the map between parallels should be constant along any single parallel, the distance on the map between meridians should be constant; for different parallels, Distance between meridians should decrease to zero towards the poles therefore, any two grid "cells" bounded by the same two parallels should enclose the same area
- 12.
- 13. Distance Property preserved TheAzimuthal Equidistant Projection North-polar aspect (Arctic at the centre) • ρ = (π / 2 − φ)R and θ = λ South-polar aspect (Antarctic at the centre) • ρ = (π / 2 + φ)R and θ = -λ Only the radial distance from the centre of the map to any object is preserved
- 14. Azimuthal Equidistant projection(North polar aspect)
- 15. Azimuthal Equidistant projection(South polar aspect)
- 16.
- 17.
- 18. Azimuthal Equal areaprojection (North polar aspect)
- 20. Self-Study http://www.progonos.com/furuti/index.html http://mathworld.wolfram.com/MapProjection.html http://mathworld.wolfram.com/Ellipse.html http://mathworld.wolfram.com/Ellipsoid.html Assignment Map Projection • Deriveequations for azimuthal equal-distance and equal area from the equatorial aspect Reference: • http://www.progonos.com/furuti/index.html • Books: – Engineering Surveying, Higher Surveying
- 21. One projection toanother
- 22.
- 23.
- 24.
- 25. Earth is nota sphere Earth mass is not distributed uniformly, so the gravitational pull is not uniform Due to rotation, equator is slightly bulged, and poles are slightly flattened (1/300) • Oblate Spheroid Terrain is not uniform
- 26. Highest spot onearth? What is the tallest peak on earth? Mount Everest, at 8,850 meters above MSL What is the highest spot on earth where you are the closest to the outer space? Mount Chimborazo, in the Andes, • 6,100 meters above MSL • But is sitting on a bulge which makes it 2,400 meters taller than Everest • Everest is sitting down on the lower side of the same bulge Source: http://www.npr.org/templates/story/story.php?storyId=9428163
- 27. Deviations (undulations) betweenthe Geoid and the WGS84 ellipsoid Source: http://www.kartografie.nl/geometrics/Introduction/introduction.html
- 28. Earth Surfaces Sea surface Geoid Ellipsoid Topographic surface Geoidis a surface of constant gravity.
- 29. Taking into accountall these irregularities is difficult Some irregularities can be ignored For e.g. terrain although important locally, terrain levels are minuscule in planetary scale • the tallest land peak stands less than 9km above sea level, or nearly 1/1440 of Earth diameter • the depth of the most profound sea abyss is roughly 1/1150 diameter.
- 30. For maps coveringvery large areas, especially worldwide, the Earth may be assumed perfectly spherical, since any shape imprecision is dwarfed by unavoidable errors in data and media resolution. Conversely, for very small areas terrain features dominate and measurements can be based on a flat Earth
- 31. Datum Horizontal Datum orGeodetic Datum Reference frame for locating points on Earth’s surface. Defines origin & orientation of latitude/longitude lines. Defined by spheroid and spheroid’s position relative to Earth’s center.
- 32. 2 types ofdatums: Earth-centered Local
- 33. Local datum coordinate system Earth-centereddatum coordinate system Earth’s S urface Earth-centered datum (WGS84) Local datum (NAD27)
- 34.
- 35. Cartesian Coordinate System WGS-84 is Earth Centered Earth Fixed; Origin to with +/- 10 cm Z Ellipsoid sized a & f Y X
- 36. Datums and Defining Parameters Totranslate one datum to another we must know the relationship between the chosen ellipsoids in terms of position and orientation. The relationship is defined by 7 constants. A. 3 - Distance of the ellipsoid center from the center of the earth (∆X, ∆Y, ∆Z) B. 3 - Rotations around the X, Y, and Z of the Cartesian Coordinate System Axes (ε, ψ, ω) C. 1 - Scale change (S) of the survey control network 2 - The size and shape of the ellipsoid (semi major axis a and flattening f approximately 1/298
- 37. Translations (3 Parameters) Movementof points along an Axis ∆X ∆Y ∆Z
- 38. Rotations (3 Parameters) Movementof points around an Axis ε ψ ω
- 39. Scale (1 Parameter) Changingthe distance between points S
- 40. Datum Transformation Simple Three-parametertransformation Geocentric translation Seven-parameter transformation Helmert 7-parameter transformation Standard Molodensky formulas
- 42.
- 44.
- 45. 3 Parameter Determination MostTransformation Parameters can be found in the NIMA technical report “Department of Defense World Geodetic System 1984” (TR 8350.2) NSN: 7643-01-402-0347
- 48.
- 50. Projection: C Datum: D (Localor global datum e.g. Indian or WGS84 Projection: A Datum: B (Local Datum e.g. Indian) Inverse mapping Geographic Coordinates Datum: B Datum Transformation Reproject to C Geographic Coordinates Datum: D Geographic Coordinates Datum: WGS 84 Datum Transformation
- 51.
- 52.
Editor's Notes
- #35 The National Imagery and Mapping Agency (NIMA) and the Defense Mapping School Reviewed by:____________Date:_________ Reviewed by:____________Date:_________ Objective: Given an overview of the National Imagery and Mapping Agency and the Defense Mapping School, the student will understand the mission issues associated with Datums, Map Projections and Coordinates. Time: 1.5 hours Training Aids and Devices: Computer, Projector/LCD Panel, Screen, Pointer, Map Examples and a PracticalExercise. Student Material and Equipment: Mapping Charting & Geodesy for the Warrior Notes. Special Requirements: None Text References: Elements of Cartography by Robinson, Geodesy for the Layman, DMA TM 8358.1; DMA TR 8350.2; TEC-SR-7;
- #37 Geodetic Datum - fixes the ellipsoid to the mean earth, basically we need to know the relationship between the chosen ellipsoid and the earth in terms of position and orientation. It is defined by 8 constants. 1. 2 - The size and shape of the ellipsoid (semi major axis and flattening) 2. 3 - The distances of the ellipsoid center from the center of the earth 3. 2 - The directions of the rotation axis with the mean rotation of the earth 4. 1 - The direction of 0 longitude with the earth’s international 0 longitude
- #41 The parameters that define the differences between 2 datums are as follows: a. The differences in meters between the two ellipsoid centers called delta x, delta y, delta z b. The rotation about the Z axis is seconds of arc between the two ellipsoids 0 longitude c. The difference in size between the two ellipsoids d. The rotations in seconds of arc about the X and Y axis, the attitude of the spin axis