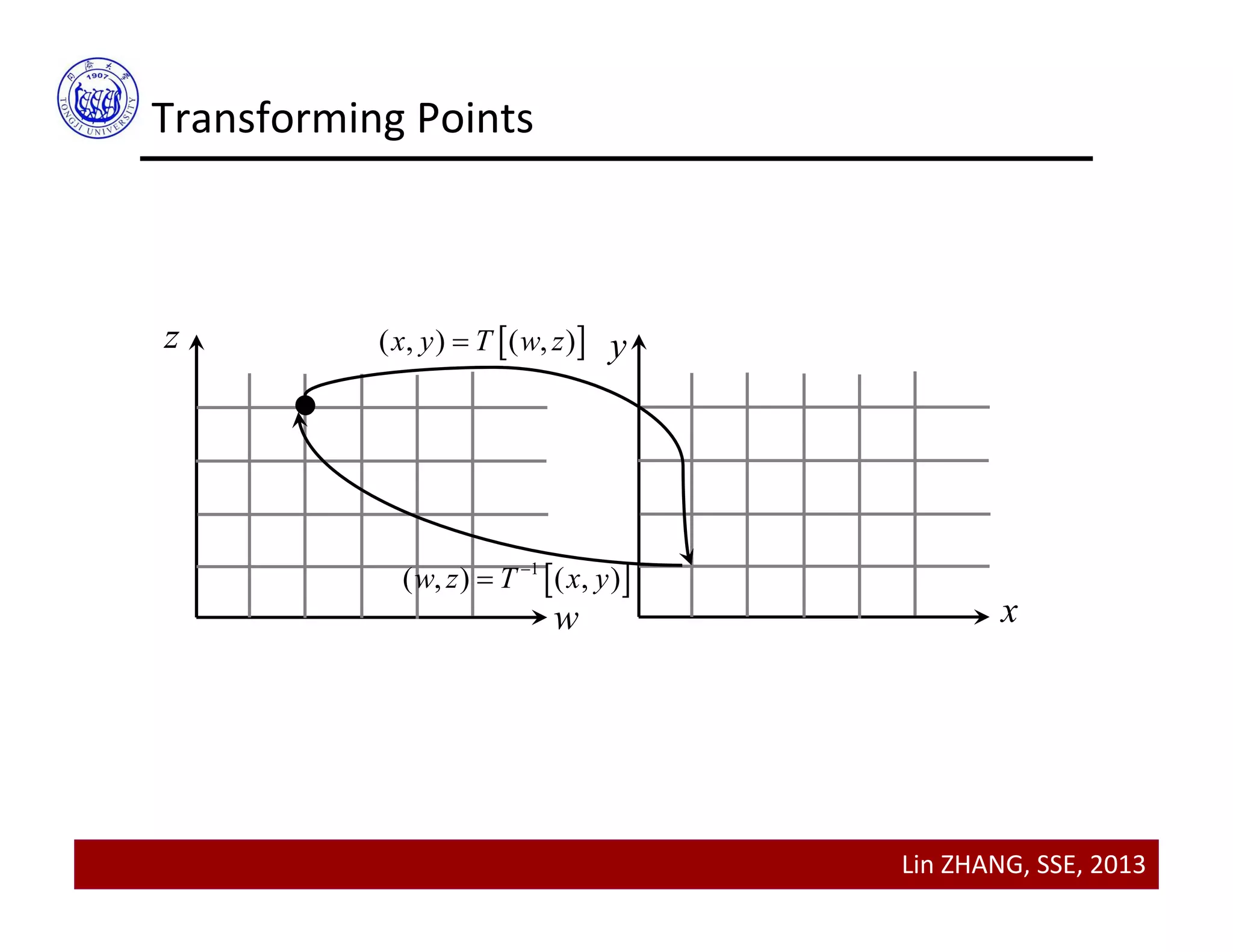
This document discusses geometric transformations and image registration. It begins by explaining how geometric transformations modify the spatial relationship between pixels in an image. It then covers transforming points using forward and inverse transformations. The rest of the document describes a hierarchy of geometric transformations including isometries, similarities, affine transformations, and projective transformations. It explains how to apply these transformations to images using interpolation and provides MATLAB examples. The document concludes by discussing image registration.











![Lin ZHANG, SSE, 2013
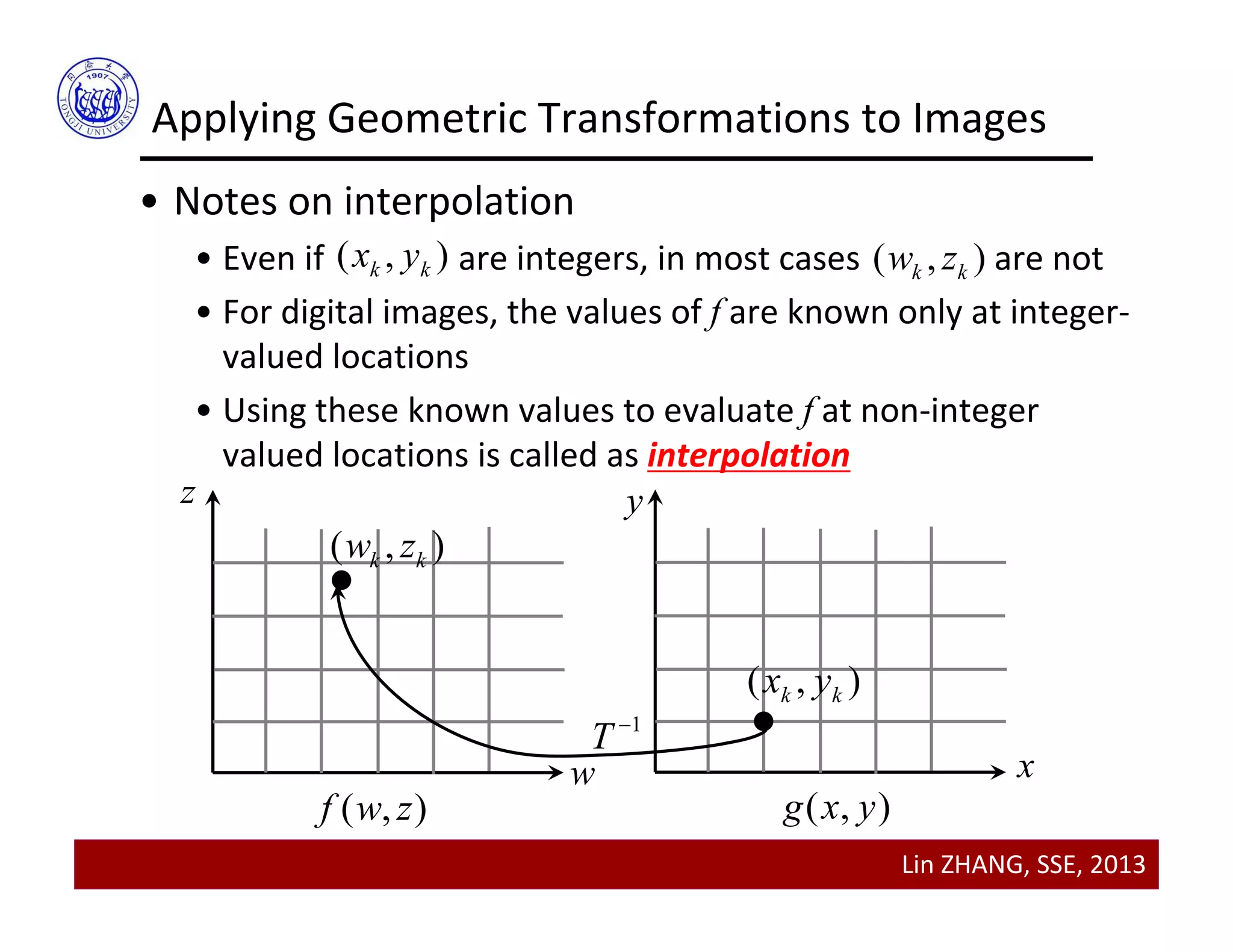
Applying Geometric Transformations to Images
• Matlab implementation
An example
im = imread('tongji.bmp');
theta = pi/6;
rotationMatrix = [cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0;0 0 1];
tformRotation = maketform('affine',rotationMatrix);
rotatedIm = imtransform(im, tformRotation,'FillValues',255);
figure;
subplot(1,2,1); imshow(rotatedIm,[]);
rotatedIm = imtransform(im, tformRotation,'FillValues',0);
subplot(1,2,2); imshow(rotatedIm,[]);](https://image.slidesharecdn.com/lecture06-geometrictransformationsandimageregistration-150420215326-conversion-gate01/75/Lecture-06-geometric-transformations-and-image-registration-21-2048.jpg)


![Lin ZHANG, SSE, 2013
Applying Geometric Transformations to Images
• Output image with location specified
An example
im = imread('tongji.bmp');
theta = pi/4;
affineMatrix = [cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0;-300 0 1];
tformAffine = maketform('affine',affineMatrix);
[affineIm, XData, YData] = imtransform(im, tformAffine,'FillValues',255);
figure; imshow(im,[]);
hold on
imshow(affineIm,[],'XData',XData,'YData',YData);
axis auto
axis on](https://image.slidesharecdn.com/lecture06-geometrictransformationsandimageregistration-150420215326-conversion-gate01/75/Lecture-06-geometric-transformations-and-image-registration-25-2048.jpg)