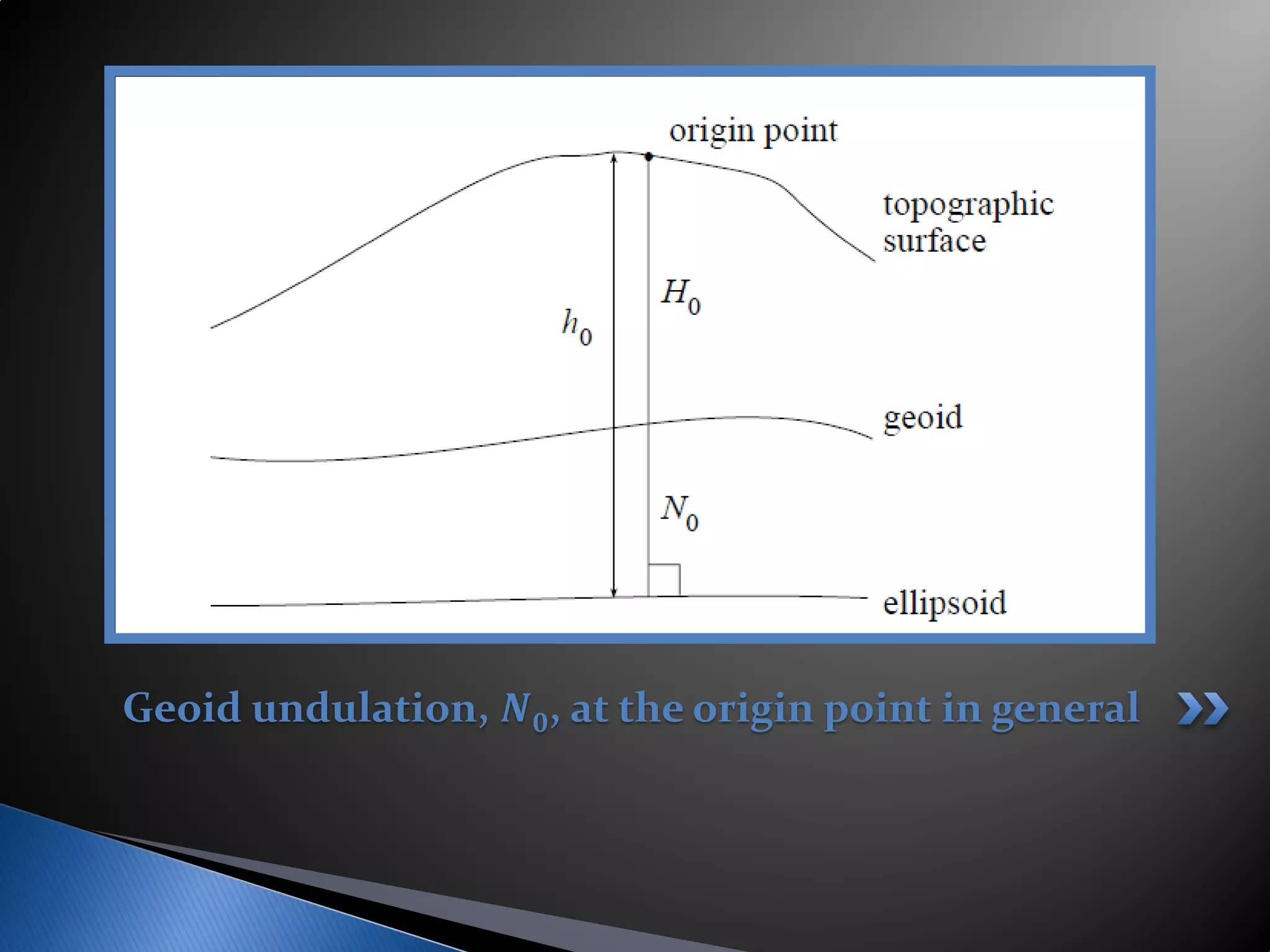
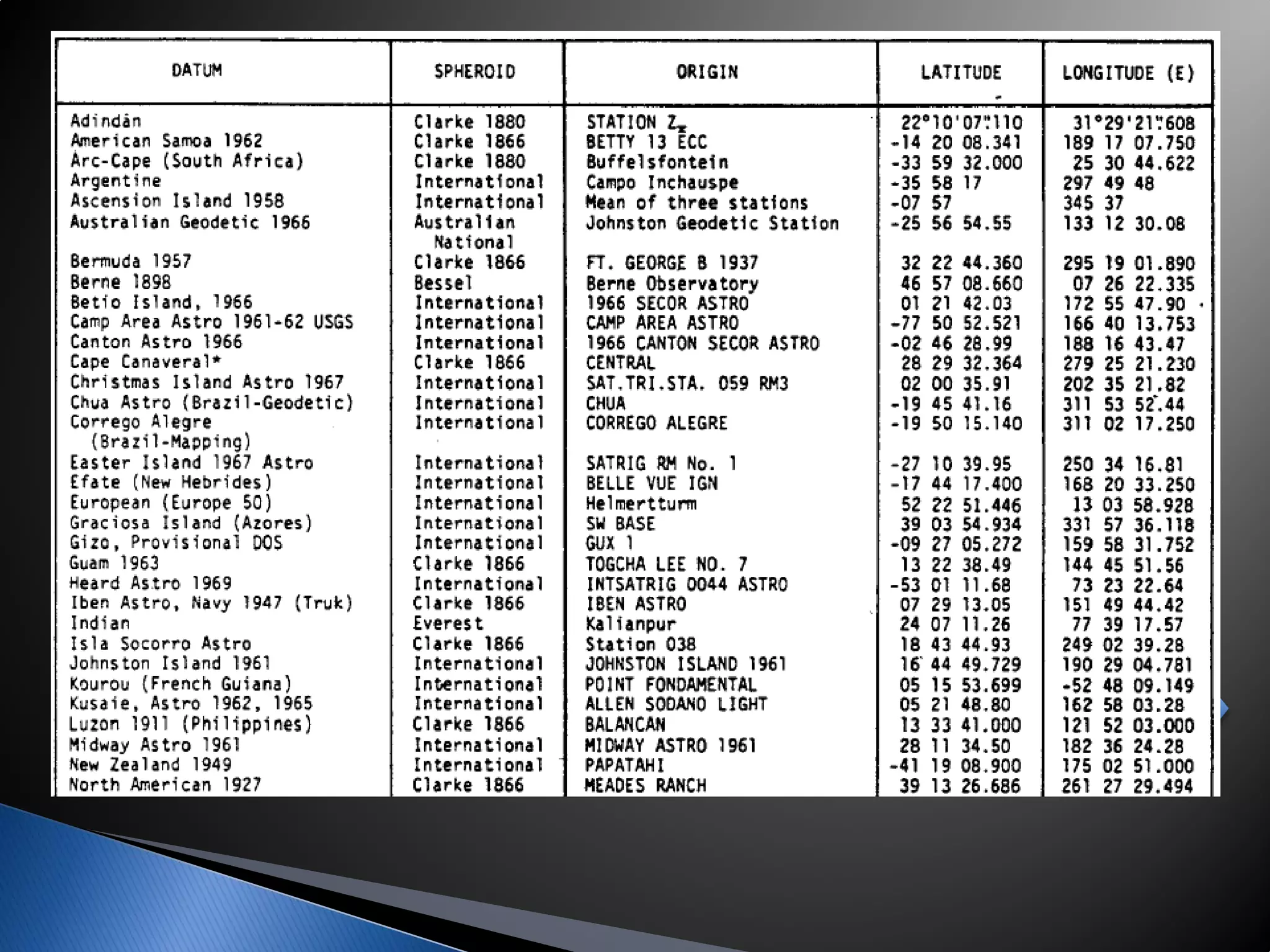
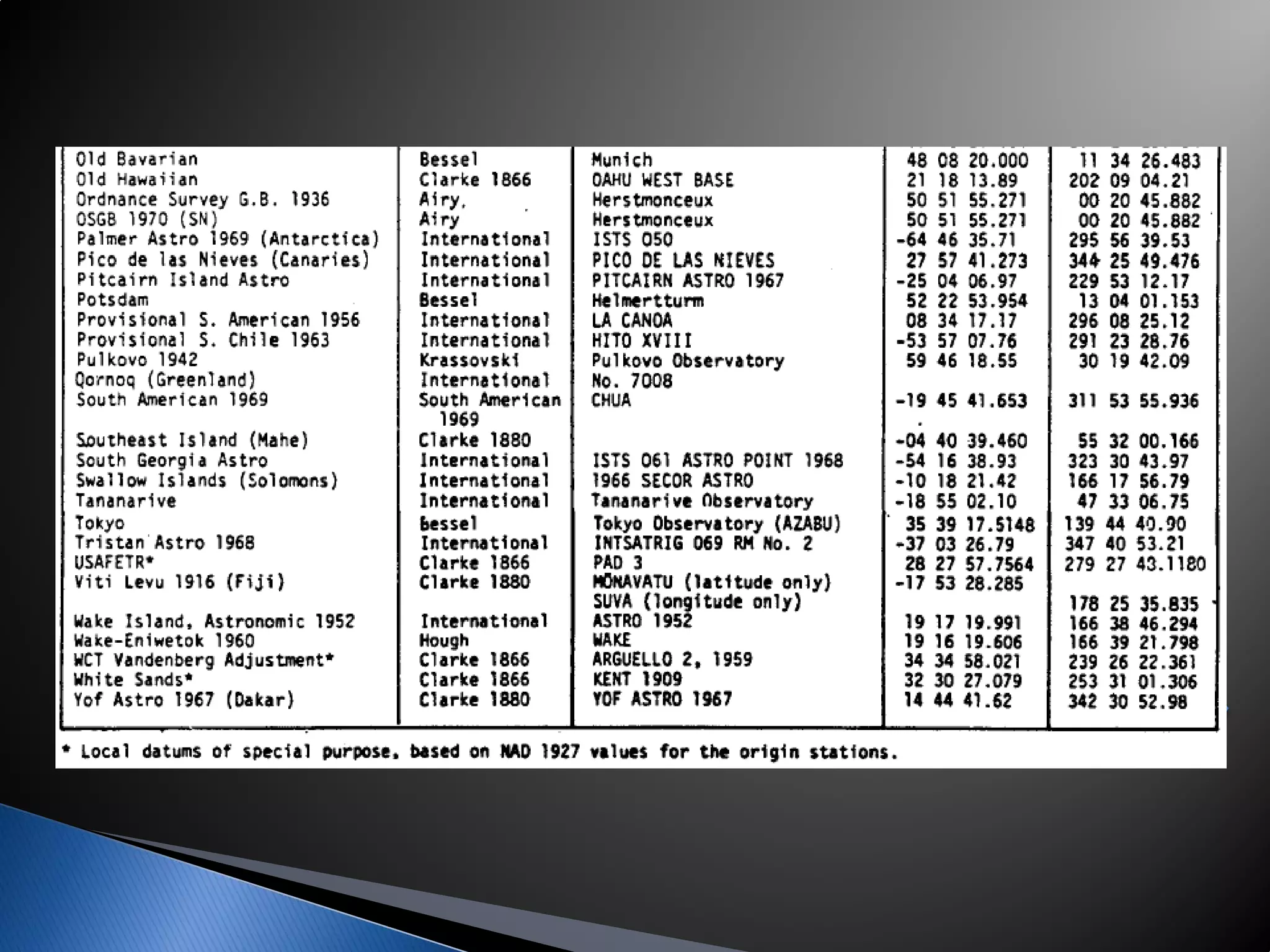
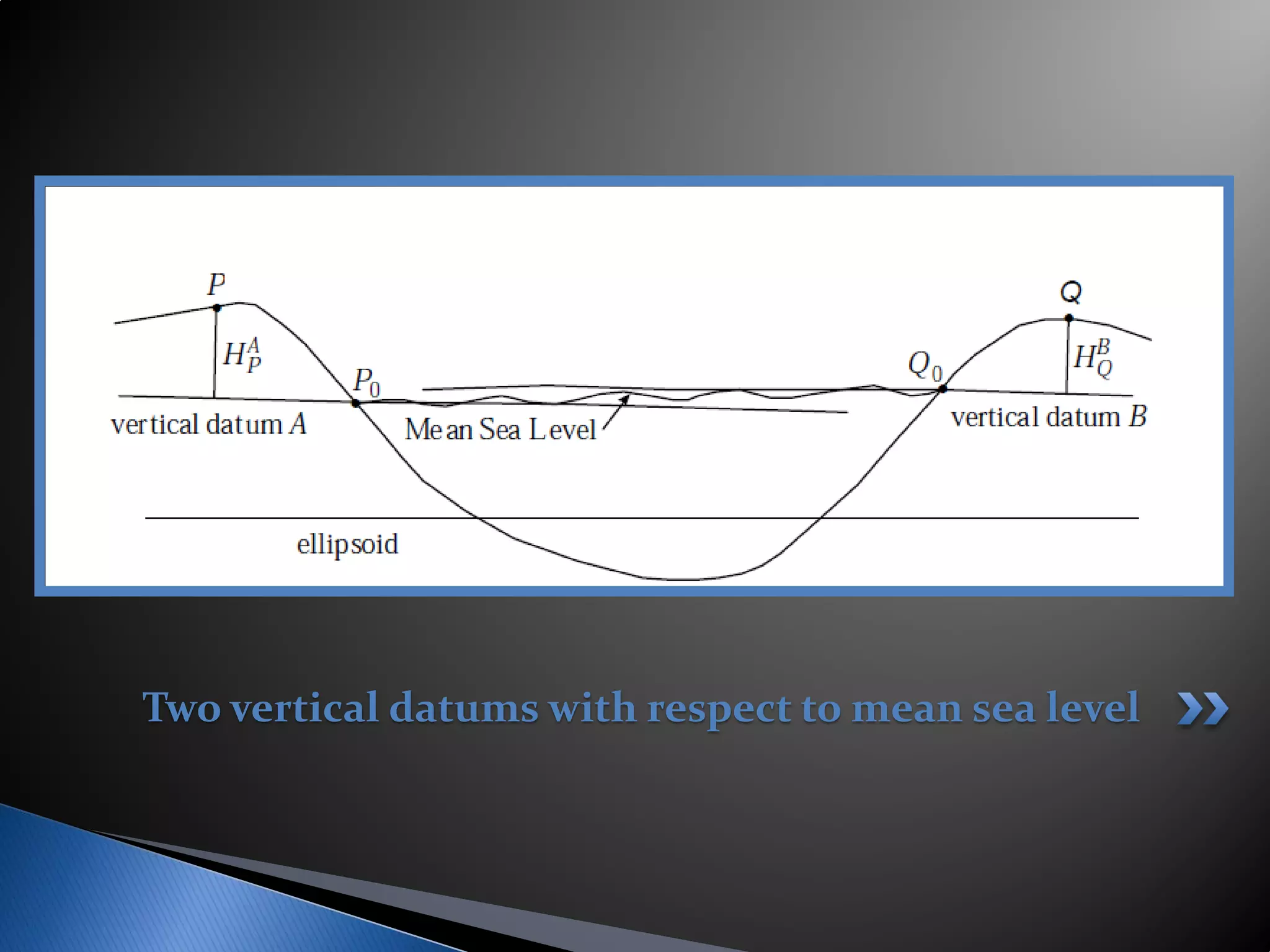
This document discusses reference systems and reference frames in geodesy. It defines a reference system as a set of prescriptions that define a coordinate axis, while a reference frame realizes the system by specifying coordinates of definite points. It describes how satellite systems like GPS have revolutionized geodetic control by providing accurate global positioning. It also defines geodetic and vertical datums, explaining that a datum defines a coordinate system through parameters like origin, orientation, and ellipsoid specification to reference geodetic applications.

1. GE 152: Reference Systems and Reference Frames
Lecture 2 – 2nd Semester 2013-2014
Lecturer: Sheryl Rose C. Reyes
Department of Geodetic Engineering

2.  A Reference System is a set of prescriptions
and conventions together with modeling
required to define at any time a triad of
coordinate axes
 A Reference Frame realizes the system by
means of coordinates of definite points that
are accessible directly by occupation or by
observation

3.  Geodetic control at local, regional, national and
international levels have been revolutionized by the advent
of satellite systems that provide accurate positioning
capability to terrestrial observers at all scales, where of
course, the Global Positioning System (GPS) has had the
most significant impact
 Countries and continents around the world are revising, re-
defining and updating their fundamental networks to take
advantage of the high accuracy, the ease of establishing
and densifying the control and critically important, the
uniformity of the accuracy and the connectivity of the
control that can be achieved basically in a global setting.

4. NGS (1986): A set of constants specifying the coordinate
system used for geodetic control, i.e., for calculating
coordinates of points on the Earth.
Torge (1991): Defines the orientation of a conventional
[coordinate] system with respect to the global X,Y,Z-
system and hence with respect to the body of the Earth
Moritz (1978): A geodetic datum is usually defined in
terms of five parameters…
Ewing and Mitchell (1970): A geodetic datum is
comprised of an ellipsoid of revolution fixed in some
manner to the physical Earth

5. A Geodetic Datum is a set of parameters and
constants that defines a coordinate system,
including its origin and (where appropriate) its
orientation and scale, in such a way as to make
these accessible to geodetic applications. (Jekeli,
2006)
Note: Conceptually, the geodetic datum defines a
coordinate system, but once the parameters that
constitute a particular datum are specified, it takes on
the definition of a frame

6.  A horizontal geodetic datum is a geodetic
datum for horizontal geodetic control in which
points are mapped onto a specified ellipsoid
 A vertical geodetic datum is a geodetic datum
for vertical geodetic control in which points
are mapped to the geopotential

7.  The definition of any terrestrial coordinate system
requires the specification of its origin and its
orientation with respect to the Earth
 If geodetic coordinates are used one must specify the
ellipsoid to which they refer
 The definition of the traditional horizontal geodetic
datum is based on eight parameters: three to define its
origin, three to define its orientation and two to define
the ellipsoid
◦ These coordinate system attributes must be accessible,, that
is for its practical utilization, the coordinate system must be
realized as a frame

8.  The origin could be defined by identifying the
point (0,0,0) of the coordinate system with
the center of mass of the Earth
◦ Prior to the emergence of artificial satellites, this
origin is not accessible
◦ The ellipsoid thus positioned relative to the Earth
rarely “fit” the region in which geodetic control
was to be established

9.  The alternative definition of the “origin”
places the ellipsoid with respect to the Earth
such that a specific point on the Earth’s
surface has given (i.e. specified or defined)
geodetic coordinates
 This datum origin point, also call the initial
datum point, is then obviously accessible – it
is a monumented marker on the Earth

10. The Datum Origin Point

12.  The coordinates (𝜙𝜙0, 𝜆𝜆0, ℎ0), of the origin point can be
chosen arbitrarily, but usually they are determined
under an imposed additional condition that the
separation between the ellipsoid and the geoid in the
particular should be minimized:
 Where 𝐻𝐻0 is the height of the origin above the geoid
(the orthometric height); this is a measurable quantity,
again defined by nature

13.  Alternatively, we could also specify the deflection of
the vertical and geoid undulation at the origin point
(𝜉𝜉0, 𝜂𝜂0, 𝑁𝑁0). Then the geodetic latitude, longitude and
ellipsoidal height are not arbitrary, but are given by the
following equations:

14. Geoid undulation, 𝑵𝑵𝟎𝟎, at the origin point in general

15.  The horizontal geodetic datum as a reference system is
defined as a system of coordinates referring to an
ellipsoid whose origin is fixed to the Earth in some
prescribed way (e.g., by “attaching” the ellipsoid to a
monument on the Earth’s surface) and whose
orientation is defined with respect to the astronomic
system
 The datum as reference frame is realized by specifying
the two ellipsoid parameters (shape and scale), the
three origin point coordinates and the three
orientation parameters

18.  A vertical datum, like a horizontal datum, requires an
origin, but being one-dimensional, there is no
orientation; and the scale is inherent in the measuring
apparatus (leveling rods)
 The origin is a point on the Earth’s surface where the
height is a defined value (e.g., zero height at a coastal
tide-gauge station)
 Traditionally, a point at mean sea level served as origin
point, but is not important what the absolute gravity
potential is at this point, since one is interested only in
height differences

19. Two vertical datums with respect to mean sea level

20.  The heights that are measured and belong to a
particular vertical datum are defined by differences
in gravity potential with respect to the origin point
 The most natural height is the orthometric height,
𝑯𝑯, defined as the distance along the (curved) plumb
line from the level surface through the datum origin
to the point being observed

21.  where 𝑁𝑁 is the distance from the ellipsoid to the level
surface through the origin point. This is the geoid
undulation only if the geoid passes through the origin
point. Otherwise, it is the geoid undulation plus the
offset of the geoid from the origin point

22.  National Geodetic Vertical Datum of 1929
(NGVD 29) – US and Canada until the 1980s
 North American Vertical Datum of 1988
(NAVD88) – US, Canada, Mexico since 1988

23.  Jekeli, Christopher. "Geometric reference systems in
geodesy." Report, Division of Geodesy and Geospatial
Science, School of Earth Sciences, Ohio State University
(2006).