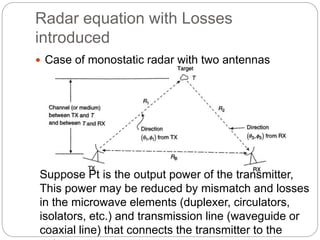
The document discusses radar equations and concepts including: 1) The radar equation relates maximum detection range to transmitted power, target radar cross section, antenna gain, and other factors. Range decreases as the fourth power of distance due to signal spreading. 2) Target radar cross section depends on the object's ability to intercept and reflect radar signals in the radar's direction. RCS can vary significantly based on the target and its orientation. 3) Losses are introduced in the radar equation from transmission inefficiencies, antenna losses, and signal attenuation over the transmission path. 4) For a given receiver sensitivity, maximum detection range increases with higher transmitted power, antenna gain, frequency, and target RCS but

1. Chapter 2
Radar Equations

2. Introduction
 Maximum detection range depends on the SNR
of the received signal:
 Transmitted power
 Target range:
As the target range is increased as the received
signal power is decreased, due to spreading over
greater and greater area of the transmitted waves.
 Antenna gain (directivity, efficient factor);
(the gain can be expressed as the ratio of the power
radiated in the direction of max radiation, to the
power that would have been radiated by a lossless
isotropic antenna.
G  D

3. Introduction
 Target radar cross section 
The targets intercepts a portion of the transmitted
signal and reflects it in various directions. How
much of the signal is intercepted, how well the
target reflects radar waves and how much of the
reflected signal is actually directed back towards the
radar, these affect and determine the size of the
target as seen by the radar. The measure of this
size is Radar Cross Section RCS ( in units area).
 Change from target to another and even from one
orientation to another of the same target.

4. RCS
 The conceptual definition of RCS includes the
fact that not all of the radiated energy falls on the
target. A target’s RCS (F) is most easily visualized
as the product of three factors:
 = Projected cross section x Reflectivity x
Directivity .
 Reflectivity: The percent of intercepted power
reradiated (scattered) by the target.
 Directivity: The ratio of the power scattered back in
the radar's direction to the power that would have
been backscattered, the scattering been uniform in
all directions (i.e. isotropically).

5. Introduction
 Antenna effective area
The reflected signal toward the radar is intercepted
by the receiving antenna, how much this area is
important, how better the level of received signal
at the receiver.
 How much the Receiving Antenna area is big,
the radar performance is better.

6. Derivation of radar equation
(monostatic radar)
 Case of no-loss path of the transmitted and reflected
waves:
1. The transmitted wave from the TX antenna has as
power Pt and it is propagated toward the target.
Pt

2. Calculate the Power density at distance R of the
target
power density
 (in the case of isotropic antenna)
4
R
2 
power density
P 
G t


 (in the case of directive antenna) Power density
4
R
2 Where G is the maximun gain of the antenna (supposing
that the target is situated at distance R inside the
main beam )

7. Derivation of radar equation
3. Calculate the Power reflected back to receiver
antenna, this is different to the power recieved by
the antenna receiver


P 
G t
4 
R
2 4. Power density of the reflected wave toward radar
P 
G t
antenna receiver is equal to:

2
2
R

4
4
R


5. Calculate the intercepted power at the antenna
P G
 
receiver, this is related to the effective t
area of the
P  
A
antenna (area where the reflected r signal  2 e
4
R
2 is
 intercepted)


8. Study of the Radar equation
 Dependance of Range
P G
t
 

P 
r A
 e
4
 2 R
4 
if R  then  r P
  r r P dB P 10 ( ) 10log
Exp:
1. R2=2R1 then Pr2 =Pr1/16
2. How many the Range should be changed to
necessitate an increasing power of 3 dB Radar
system where RCS, f, Ae, G constant values,
gives.

9. Study of the Radar equation
 Dependence on frequency
 Ae is related to G,
2 2 2
G P G
P G

P t t
r
2 4 4 4 4 R
  R
  3 4
restriction of this formula…..
 More representative formula
2
arg f P f
4 4
P  A  A 
Ae
t eT et
P r
r   
4 4
c 
R

 VHF : 30 MHZ  300 MHZ, increasing of 40 dB
 UHF: 300 MHZ 1GHZ, increasing of 20.89 dB
 Lband: 1GHZ 2GHZ, increasing of 12 dB
P K f r dB   40log

 


   
 
 


10. Maximum detection range
 The max detection Range Rmax is ultimately determined
by the minimum signal to noise ratio required by the
receiver.
 For a given noise level at the input of the receiver, the
minimum signal to noise ratio depends on the minimum
detectable signal power Smin, A signal 
weaker than Smin,
would covered by noise and would probably not be
detected.

 P  G  A


R t e

4 


max 2
 
1/ 4
min


S

 Consequently for long ranges, the following parameters
t P
should be chosen accordingly:
 must be higher
 G must be higher
 Smin must be low (receiver ability to detect weak signal level)
2
arg
P  A  A 
Ae
R t eT et 
2 2

   
 Rmax in terms of transmitted frequency:
f
S
 4
min
max
 
4
min
3
max
4  

 


S
P G
R t

 
and

11. Radar equation with Losses
introduced
 Case of monostatic radar with two antennas
Suppose Pt is the output power of the transmitter,
This power may be reduced by mismatch and losses
in the microwave elements (duplexer, circulators,
isolators, etc.) and transmission line (waveguide or
coaxial line) that connects the transmitter to the
antenna.

12. Radar equation with Losses
introduced
If 퐿푡 = Power loss transmitter to antenna with 퐿푡 ≥ 1
Then the average peak power accepted at the receiver antenna is
denoded as Pacc, where:
푃푎푐푐 =
푃푡
퐿푡
Lrt (radiation loss of the transmitting antenna) because some power
is lost through heating effects in the structure of the antenna. This
loss is denoted by and defined by:
퐿푟푡 =
1
휚푟푡
≥ 1
휚푟푡 is the efficiency of the transmitting antenna
With these losses the average peak radiated power is :
푃푟푎푑 =
푃푎푐푐
퐿푟푡
=
푃푡
퐿푡 × 퐿푟푡

13. Radar equation with Losses
introduced
 If all the average peak radiated power occurred from a
nondirective (isotropic) antenna, the power density of the
wave at distance R1 would be:
푃푡
4휋푅1
2 ×
1
퐿푐ℎ1
where Lch1 is the one path medium loss (due to all clear and
unclear channel effects that may be present (atmospheric
attenuations, effects of rain, snow, etc. )
푃푡
4휋푅1
2 ×
1
퐿푐ℎ1
×
1
퐿푡
×
1
퐿푟푡
If the antenna is directive with Gain 퐺(휃1, 휑1) in the direction
of the target, then the power density toward the target
direction is:
푃푡
4휋푅1
2 ×
1
퐿푐ℎ1
×
1
퐿푡
×
1
퐿푟푡
× 퐺(휃1, 휑1)

14. Radar equation with Losses
introduced
 The reflected power from the target in the
direction of the receiving antenna is given by:
푃푡
4휋푅1
2 ×
1
퐿푐ℎ1
×
1
퐿푡
×
1
퐿푟푡
× 퐺(휃1, 휑1) × 휎
The reflected power received by the RX antenna:
푃푡
4휋푅1
2 ×
1
퐿푐ℎ1
×
1
퐿푡
×
1
퐿푟푡
× 퐺(휃1, 휑1) × 휎 ×
1
퐿푐ℎ2
×
1
4휋푅2
2 × 퐴푒

15. Radar equation with Losses
introduced
 The received power is then equal to:
푆푟 =
푃푡 × 퐺 휃1, 휑1 × 휎 × 퐴푒
2푅2
4휋푅1
2 ×
1
퐿푐ℎ1퐿푐ℎ2퐿푡퐿푟푡퐿푟푟
Where Lrr is the antenna receiving loss :
퐿푟푟 =
1
휚푟푟
≥ 1
And also,
푆푟
=
푃푡 × 퐺 휃1, 휑1 × 휎 × 퐺(휃3, 휑3) × 휆2
2푅2
(4휋)3 × 푅1
2 ×
1
퐿푐ℎ1퐿푐ℎ2퐿푡퐿푟푡퐿푟푟

16.  Example
find the maximum range R of a monostatic radar
(with same antenna of trasmission and reception)
that must provide an available received average
peak signal power of 10- 12 W when frequency is
4.6 GHz, Pt = 104 W, the antenna's aperture area is
2.0 m2 , aperture efficiency is 0.64, radar cross
section is 1.4 m2 , loss of transmitting antenna is
1.2, loss of antenna’s radiation = 1.04, and loss of
path = 1.43.