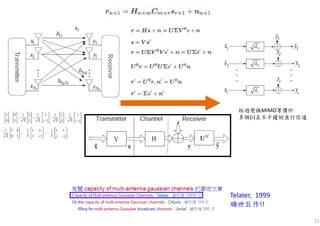
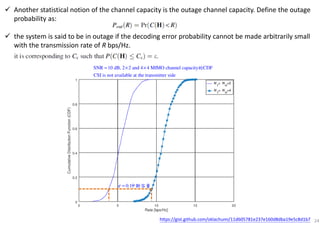
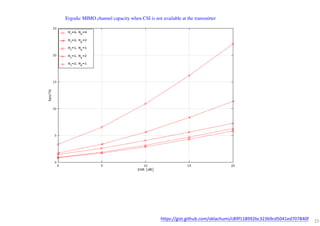
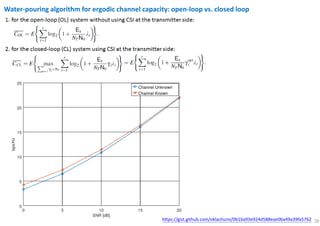
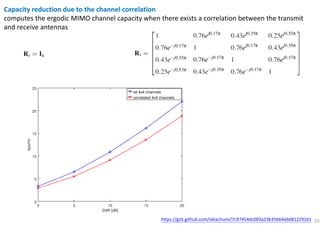
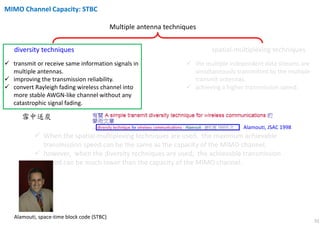
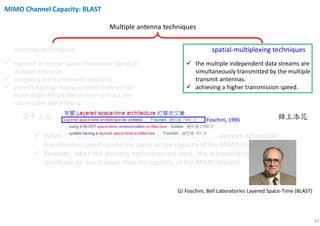
The document discusses the channel capacity of MIMO (Multiple Input Multiple Output) systems, focusing on various techniques such as spatial multiplexing and diversity techniques. It highlights the importance of channel state information (CSI) availability at the transmitter and outlines the capacity implications of different transmission strategies. Additionally, it explores the water-pouring algorithm and the concept of ergodic channel capacity in the context of random MIMO channels.

1. MIMO: Channel Capacity
Jay Chang
1

2. 2
Useful Matrix Theory
Deterministic MIMO Channel Capacity
• CSI is Known to the Transmitter Side
• CSI is Not Available at the Transmitter Side
Channel Capacity of Random MIMO Channels
Agenda

3. 3
Multiple antenna techniques
diversity techniques spatial-multiplexing techniques
transmit or receive same information signals in
multiple antennas.
improving the transmission reliability.
convert Rayleigh fading wireless channel into
more stable AWGN-like channel without any
catastrophic signal fading.
the multiple independent data streams are
simultaneously transmitted by the multiple
transmit antennas.
achieving a higher transmission speed.
When the spatial-multiplexing techniques are used, the maximum achievable
transmission speed can be the same as the capacity of the MIMO channel;
however, when the diversity techniques are used, the achievable transmission
speed can be much lower than the capacity of the MIMO channel.
雪中送炭 錦上添花
MIMO: Channel Capacity
Li Zhong and D. Tse, IEEE IT 2003

4. 4
2log (1 ) log( )C B SNR C r SNR= + ⇒ =
: log d
e SNR e eP P d P SNR−
⇒ = − ⇒ =無編碼情況下的誤符號率

5. 5
Prof. Li Zhong Zheng (MIT)
Prof. 王奕翔 (NTU)
P.S.
……

6. 6
Useful Matrix Theory
Deterministic MIMO Channel Capacity
• CSI is Known to the Transmitter Side
• CSI is Not Available at the Transmitter Side
Channel Capacity of Random MIMO Channels
Agenda

7. 7
Useful Matrix Theory
min1. TxN N= min2. RxN N=
3. Given SVD of H

8. 8
4. For a non-Hermitian square matrix (non-symmetric real matrix)n n×
∈ℂH
1
the eigenvectors of a non-Hermitian matrix are not orthogonal.
the eigenvectors of a Hermitian matrix are orthogonal.( )
n n
n n H
Q Q
×
× −
∈
∈ =
ℂ
ℂ
H
H
5. the squared Frobenius norm of the MIMO channel is interpreted as a total power gain of the channel.

9. 9
Useful Matrix Theory
Deterministic MIMO Channel Capacity
• CSI is Known to the Transmitter Side
• CSI is Not Available at the Transmitter Side
Channel Capacity of Random MIMO Channels
Agenda

10. 10
Deterministic MIMO Channel Capacity
narrowband time-invariant wireless channel can be represented by deterministic matrix Rx TxN N
Rx TxN N ×
× ∈ℂH
Ex為發送端一個符號週期的平均能量
1
1
1

11. 11
Channel Capacity when CSI is Known to the Transmitter Side
given that H(z) is a constant, we can see that the
mutual information is maximized when H(y) is
maximized.
Ex為發送端一個符號週期的平均能量

12. 12
Telater, 1999
曠世巨作!!
經過變換MIMO等價於
多個(r)互不干擾的並行信道

13. 13
Telatar, European Transactions on Telecommunications 1999
Modal decomposition when CSI is available at the transmitter side.

14. 14
The MIMO channel capacity is now given by a sum of the capacities of the virtual SISO channels
By solving the following
power allocation problem
solution to the optimization problem is
Well-known as water-pouring algorithm, Gallager 1968.
more power must be allocated to the mode with higher SNR.

15. 15
Lagrange multiplier solve optimization problems
maximize ( , )
subj
optimization problem
ect to ( , ) 0
( , , ) ( , ) (
:
, )
f x y
g x y
L x y f x y g x yλ λ
=
= − ⋅

16. 16https://en.wikipedia.org/wiki/Water-pouring_algorithm
如果信號的功率為P = P1 + P2, 可以驗證一個公式:
C = log(1 + (P1 + P2)/N) = log(1 + P1/N) + log(1 + P2/(P1 + N)) = C1 + C2.
C1 = log(1 + P1/N)可理解為信號功率P1, 噪聲為N時的容量,
C2 = log(1 + P2/(P1 + N))可理解為信號功率P2, 噪聲為(P1 + N)時的容量. 有人把這個叫superposition coding.
也就是說, 這兩份功率, 第一份功率產生了一個容量, 同時等效成了對第二份功率的噪聲.
如果有N個並行的通道, 這N個通道上已經有一些噪聲或者信號的功率.
如果我再有一小份功率, 把它分配到哪個通道上能獲得最大的通道容量呢 ?
從上面的分析我們知道, 已經存在的功率, 無論是噪聲還是信號, 對後來的信號來說都是噪聲,
因此, 這一小份功率分配到累計功率最小的通道上獲得的容量最大.
這樣分配的結果就是N個通道上的功率是相同的, 就是注水定理. 注水定理可以看作是通道容量的動態過程.
water-pouring theory

17. 17
water filling theory (注水定理注水定理注水定理注水定理)
1 2 1 2
1 2 1 2
1
1
1 1
2
2
1
AWGN :
: , : , : ,
log(1 ), : , : , :
If , then log(1 ) log(1 ) log(1 )
log(1 ), , ;
log(1 ),
Y X Z
X Z Y
P
C C P N
N
P P P P
P P P C C C
N N P N
P
C P N
N
P
C
P N
= +
= +
+
= + = + = + + + = +
+
= +
= +
+
一個 信道
輸入信號 白噪聲 輸出信號 皆為複隨機變量.
信道容量 輸入信號功率 噪聲功率
信號功率
信號功率 噪聲 時的容量
信 2 1,
,
P P N+
第一份功率產生的容量 同時等效成對
號功率 噪聲 時的
第二份功
容量
率的噪聲
如果有N個並行的信道, 這N個信道上已經有一些噪聲或者信號的功率, 如果我再有一小份功率, 把它分配到
哪個信道上能獲得最大的信道容量呢 ?
從上面的分析我們知道, 已經存在的功率, 無論是噪聲還是信號, 對後來的信號來說都是噪聲.
因此, 這一小份功率分配到累計功率最小的信道上獲得的容量最大. 這樣分配的結果就是N個信道上的功率
是相同的, 就是注水定理.

18. 18
Useful Matrix Theory
Deterministic MIMO Channel Capacity
• CSI is Known to the Transmitter Side
• CSI is Not Available at the Transmitter Side
Channel Capacity of Random MIMO Channels
Agenda

19. 19
Channel Capacity when CSI is Not Available at the Transmitter Side
when CSI is not available at the transmitter and thus, the total power is equally allocated to all transmit antennas.
MIMO capacity is maximized when the channel is orthogonal. its capacity to N times that of each parallel channel.
2 2
0
log 1 xE
C N
N N
ζ 
= + 
 
2 2
2
0
if
log 1
MIMO SISO .
F
x
N
E
C N
N
N
ζ= =
 
= + 
 
正交 信道容量是 的 倍
H

20. 20
Channel Capacity of SIMO and MISO Channels
Although the maximum achievable transmission speeds of the two systems are the same, there are various ways to utilize the
multiple antennas, for example, the space-time coding technique, which improves the transmission reliability.
Without CSI same with SISO.
With/Without CSI.

21. 21
Channel Capacity of MISO Channels with CSI available
With CSI.

22. 22
Useful Matrix Theory
Deterministic MIMO Channel Capacity
• CSI is Known to the Transmitter Side
• CSI is Not Available at the Transmitter Side
Channel Capacity of Random MIMO Channels
Agenda

23. 23
In general, MIMO channels change randomly. Therefore, H is a random matrix, which means that its
channel capacity is also randomly time-varying.
In practice, we assume that the random channel is an ergodic process. Then, we should consider
the following statistical notion of the MIMO channel capacity:
Channel Capacity of Random MIMO Channels
ergodic process: 統計平均 = 樣本的時間平均
ergodic channel capacity
1. for the open-loop (OL) system without using CSI at the transmitter side:
2. for the closed-loop (CL) system using CSI at the transmitter side:

24. Another statistical notion of the channel capacity is the outage channel capacity. Define the outage
probability as:
the system is said to be in outage if the decoding error probability cannot be made arbitrarily small
with the transmission rate of R bps/Hz.
24
0.1ε = 中斷容量
https://gist.github.com/oklachumi/11d605781e237e160d8dba19e5c8d1b7
SNR 10 dB, 2 2 and 4 4 MIMO channel capacity CDF
CSI is not available at the transmitter side
= × × 的

25. 25
Ergodic MIMO channel capacity when CSI is not available at the transmitter
https://gist.github.com/oklachumi/c89f118992bc323b9cd5041ed707840f

26. 26
Water-pouring algorithm for ergodic channel capacity: open-loop vs. closed loop
https://gist.github.com/oklachumi/0b1ba93e924d588eae06a49a39fa5762

27. 27
MIMO channel gains between transmit and received antennas are correlated
In general, the MIMO channel gains are not independent and identically distributed (i.i.d.).
When the SNR is high, the deterministic channel capacity can be approximated as
constant
• Rt is the correlation matrix, reflecting the correlations between the transmit antennas (i.e., the
correlations between the column vectors of H).
• Rr is the correlation matrix reflecting the correlations between the receive antennas (i.e., the
correlations between the row vectors of H).
• Hw denotes the i.i.d. Rayleigh fading channel gain matrix.
• The diagonal entries of Rt and Rr are constrained to be a unity.
MIMO channel capacity has been reduced, and the amount of capacity reduction (in bps) due to
the correlation between the transmit and receive antennas is
< 0
R is a symmetric matrix , Q is a unitary matrix.

28. 28
R is a symmetric matrix , Q is a unitary matrix.
pf:
The equality in Equation holds when the
correlation matrix is the identity matrix.

29. 29
Capacity reduction due to the channel correlation
computes the ergodic MIMO channel capacity when there exists a correlation between the transmit
and receive antennas
https://gist.github.com/oklachumi/7c97454dc003a23b35664eb681229161

30. 30
Multiple antenna techniques
diversity techniques spatial-multiplexing techniques
transmit or receive same information signals in
multiple antennas.
improving the transmission reliability.
convert Rayleigh fading wireless channel into
more stable AWGN-like channel without any
catastrophic signal fading.
the multiple independent data streams are
simultaneously transmitted by the multiple
transmit antennas.
achieving a higher transmission speed.
When the spatial-multiplexing techniques are used, the maximum achievable
transmission speed can be the same as the capacity of the MIMO channel;
however, when the diversity techniques are used, the achievable transmission
speed can be much lower than the capacity of the MIMO channel.
雪中送炭 錦上添花
MIMO: Channel Capacity

31. 31
Multiple antenna techniques
diversity techniques spatial-multiplexing techniques
transmit or receive same information signals in
multiple antennas.
improving the transmission reliability.
convert Rayleigh fading wireless channel into
more stable AWGN-like channel without any
catastrophic signal fading.
the multiple independent data streams are
simultaneously transmitted by the multiple
transmit antennas.
achieving a higher transmission speed.
When the spatial-multiplexing techniques are used, the maximum achievable
transmission speed can be the same as the capacity of the MIMO channel;
however, when the diversity techniques are used, the achievable transmission
speed can be much lower than the capacity of the MIMO channel.
雪中送炭 錦上添花
MIMO Channel Capacity: STBC
Alamouti, space-time block code (STBC)
Alamouti, JSAC 1998

32. 32
Multiple antenna techniques
diversity techniques spatial-multiplexing techniques
transmit or receive same information signals in
multiple antennas.
improving the transmission reliability.
convert Rayleigh fading wireless channel into
more stable AWGN-like channel without any
catastrophic signal fading.
the multiple independent data streams are
simultaneously transmitted by the multiple
transmit antennas.
achieving a higher transmission speed.
When the spatial-multiplexing techniques are used, the maximum achievable
transmission speed can be the same as the capacity of the MIMO channel;
however, when the diversity techniques are used, the achievable transmission
speed can be much lower than the capacity of the MIMO channel.
雪中送炭 錦上添花
MIMO Channel Capacity: BLAST
GJ Foschini, Bell Laboratories Layered Space-Time (BLAST)
Foschini, 1996

33. 33
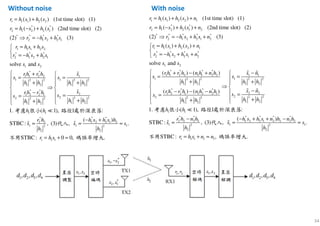
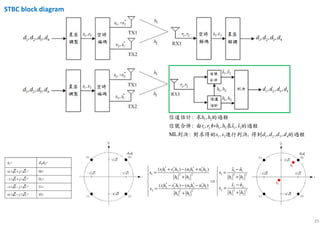
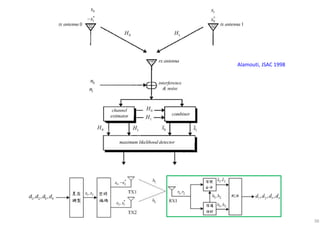
Space-Time Block Code
Space-Time Block Code (STBC)
• h1 and h2 are impulse
responses of two channels
whose envelopes follow
Rayleigh distribution
[ ]
*
1 2
1 2 *
2 1
x x
x x
x x
 −
→  
 
1 *
1 2x x = − x
2 *
2 1x x =  x
1 2 * *
1 2 2 1 0x x x x⋅ − =< x x > =
( )
* * *
1 2 1 2
*
2 1 2 1
2 2
2 21 2
1 22 2
1 2
,
0
0
x x x x
x x x x
x x
x x
x x
   −
= =   
−   
 +
 ⋅ = = +
 + 
H
H
2
X X
X X I
where x1, x2 are modulated symbols
The received vectors are
1 1 1 2 2 1
* *
2 1 2 2 1 2
* * * *
2 1 2 2 1 2
1 1 2 1 1
* * * *
2 2 1 2 2
1 2 1
* *
2 1 2
( ) ( ) (1st time slot)
( ) ( ) (2nd time slot)
( ) ( )
. To solve we need to
y h x h x n
y h x h x n
y h x h x n
y h h x n
y h h x n
h h x
h h x
= + +
= − + +
= − + +
       
= +       −       
   
≡    −   
H find the inverse of .H
( )
( )
( )
2 2*
1 21 21 2
* ** 2 2
2 12 1 1 2
2 2
1 2
2 2
1 2
1 1
*
2 2
1
1
1
0
0
digonal matrix inverse is
1
0
1
0
the estimate of the tramsmitted symbol is
H H
H
H
H H
H H H
H H
H H
h hh hh h
h hh h h h
h h
H H
h h
x y
x y
H
−+
−
−
 +   
 =   −−  +    
 
 
+ 
 
 
+  
 
=

=


=
=
H
( )
( )
1 1
*
2 2
1 1
*
2 2
1
1
H H
H H
x n
H
x n
H H H
H H
n
x
H
x
n
−
−
 
 
 
   
= +   
 
 
    
=
   
+   
   
For a general m*n matrix the pseudo inverse is defined as
線代啟示錄 Moore-Penrose 偽逆矩陣

34. 34
1 1 1 2 2 1
* *
2 1 2 2 1 2
* * * * *
2 1 2 2 1 2
1 1 1 2 2 1
* * * *
2 1 2 2 1 2
1 2
* * *
1 1 2 2 1 1
1
( ) ( ) (1st time slot) (1)
( ) ( ) (2nd time slot) (2)
(2) (3)
( ) ( )
solve and
( ) (
r h s h s n
r h s h s n
r h s h s n
r h s h s n
r h s h s n
s s
rh r h n h
s
= + +
= − + +
⇒ = − + +
= + +

= − + +
+ −
=
*
2 2 1 1
12 2 2 2
1 2 1 2
* * * *
2 21 2 2 1 1 2 2 1
2 2 22 2 2
1 21 2
1 1
* * * * * *
2 2 2 2 1 2 2 1 2 2 2 2
1 1 12 2
2 2
)
( ) ( )
1. ( 1), 1 :
( )
ˆ ˆSTBC : , (3) , .
STB
n h s n
s
h h h h
s nrh r h n h n h
ss
h hh h
h h
r h n h h s h s n h n h
s s s
h h
 + −
= 
+ + 
⇒ 
−− − −  ==
  ++ 
− − + + −
≈ ≈ ≈
ɶ ɶ
ɶ ɶ
≪考慮 很小 路徑 處於深衰落
代入
不用 1 1 1 1 1C: , .r h s n n= + ≈ 碼誤率增大
1 1 1 2 2
* *
2 1 2 2 1
* * * *
2 1 2 2 1
1 1 1 2 2
* * *
2 1 2 2 1
1 2
* *
1 1 2 2
1 2 2
1 2
* *
1 2 2 1
2 2 2
1 2
( ) ( ) (1st time slot) (1)
( ) ( ) (2nd time slot) (2)
(2) (3)
solve and
r h s h s
r h s h s
r h s h s
r h s h s
r h s h s
s s
rh r h
s
h h
rh r h
s
h h
= +
= − +
⇒ = − +
= +

= − +
 +
=
+

−
=
+
1
1 2 2
1 2
2
2 2 2
1 2
1 1
* * *
2 2 1 2 2 1 2
1 1 12 2
2 2
1 1 1
1. ( 1), 1 :
( )
ˆ ˆSTBC: , (3) , .
STBC: 0 0, .
s
s
h h
s
s
h h
h h
r h h s h s h
s s s
h h
r h s

= 
+ 
⇒ 
  =
  +
− +
≈ ≈ ≈
= + ≈
ɶ
ɶ
≪考慮 很小 路徑 處於深衰落
代入
不用 碼誤率增大
Without noise With noise

35. 35
1 2
1 2 1 2 1 2
1 2 1 2 3 4
: ,
: , , ,
ML : , , , , ,
h h
r r h h s s
s s d d d d
ɶ ɶ
信道估計 求 的過程
信號合併 由 和 求 的過程
判決 對求得的 進行判決 得到 的過程
* * * *
1 1 2 2 1 1 2 2 1 1
1 12 2 2 2
1 2 1 2
* * * *
2 21 2 2 1 1 2 2 1
2 2 22 2 2
1 21 2
( ) ( )
( ) ( )
rh r h n h n h s n
s s
h h h h
s nrh r h n h n h
ss
h hh h
 + − + −
= = 
+ + 
⇒ 
−− − −  ==
  ++ 
ɶ ɶ
ɶ ɶ
STBC block diagram

36. 36
Alamouti, JSAC 1998

37. 37

38. 38

39. 39