الوثيقة تحتوي على ملخصات لقوانين الجبر والإحصاء والهندسة، موضحة الخصائص الأساسية والقواعد المتعلقة بالحسابات الجبرية وعمليات الاحتمال. كما تتضمن نظريات هندسية تتعلق بالدائرة، القطر والمماس وخصائص الزوايا المتعددة. يركز المحتوى على تطبيقات الرياضيات في مجالات متنوعة ويتضمن مجموعة من البرهانات الرياضية.

1. ‫الجبر‬ ‫قوانين‬ ‫ملخص‬ : ‫-أول‬
1‫ب‬ ± ‫ب‬ - = ‫س‬ ‫العام‬ ‫القانون‬ -2
–4‫جـ‬ ‫أ‬
2‫أ‬
2‫المقام‬ ‫أصفار‬ ‫مجموعة‬ – ‫ح‬ = ‫الجبري‬ ‫الكسر‬ ‫مجال‬ -
3‫المقام‬ ‫أصفار‬ ‫مجموعة‬ – ‫ح‬ = ‫الجمعي‬ ‫المعكوس‬ ‫مجال‬ -
4‫المقام‬ ‫و‬ ‫البسط‬ ‫أصفار‬ ‫مجموعة‬ – ‫ح‬ = ‫الضربي‬ ‫المعكوس‬ ‫-مجال‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ثانيا‬:‫قوانين‬ ‫ملخص‬‫التحتمال‬
1(‫أ‬ )‫ل‬U( ‫ب‬ ∩ ‫أ‬ )‫ل‬ – ( ‫ب‬ )‫ل‬ + ( ‫أ‬ ) ‫ل‬ = ( ‫ب‬
2(‫أ‬ )‫ل‬ – ( ‫ب‬ )‫ل‬ + ( ‫أ‬ ) ‫ل‬ = ( ‫ب‬ ∩ ‫أ‬ )‫ل‬U( ‫ب‬
3((‫ب‬ ∩ ‫أ‬ )‫ل‬ – ( ‫أ‬ ) ‫ل‬ =( ‫ب‬ – ‫ل)أ‬
4(= ( َ ‫أ‬ ) ‫ل‬1= ( َ ‫ل)عفريت‬ ( ‫أ‬ )‫ل‬ –1( ‫عفريت‬ )‫ل‬ –
5(= ‫ب‬ ∩ ‫أ‬ ‫فإن‬ ‫متنافيان‬ ‫تحدثان‬ ‫ب‬ ، ‫أ‬ ‫كان‬ ‫إذا‬ф= ( ‫ب‬ ∩ ‫أ‬ )‫ل‬ ،0
6(‫أ‬ ‫كان‬ ‫إذا‬‫כ‬‫أ‬ )‫ل‬ ،( ‫أ‬ )‫ل‬ = ( ‫ب‬ ∩ ‫أ‬ )‫ل‬ ‫فإن‬ ‫ب‬U(‫ب‬ )‫ل‬ = ( ‫ب‬
7(= ‫والمؤكد‬ ‫صفر‬ = ‫المستحيل‬ ‫الحدث‬ ‫اتحتمال‬1)‫ل‬ ،ф)=0
8(0≥ ( ‫)أ‬ ‫ل‬ ≥1‫تحدث‬ ‫أي‬ ‫وقوع‬ ‫اتحتمال‬ ‫أن‬ ‫أي‬‫כ‬]0،1[
9((‫ن)أ‬ = (‫ل)أ‬ ‫أن‬ ‫أي‬ ‫عناصرالحدث‬ ‫عدد‬ = ‫تحدث‬ ‫وقوع‬ ‫اتحتمال‬
(‫ن)ف‬ ‫العينة‬ ‫فضاء‬ ‫عناصر‬ ‫عدد‬
10‫الحتحاد‬ ) (U( ‫معا‬ = ‫و‬ = ∩ ‫التقاطع‬ ) ( ‫القل‬ ‫على‬ = ‫أو‬ =
(‫أ‬ ‫وقوع‬ ‫عدم‬ =‫المكملة‬ ) (‫ب‬ ‫وقوع‬ ‫وعدم‬ ‫أ‬ ‫وقوع‬ = ‫فقط‬ ‫أ‬ = ‫)الفرق‬
11= َ ‫أ‬ ∩ ‫أ‬ (ф‫أ‬ ،U)‫ل‬ ، ‫ف‬ = َ ‫أ‬ф)=0= ( ‫ف‬ )‫ل‬ ،1
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
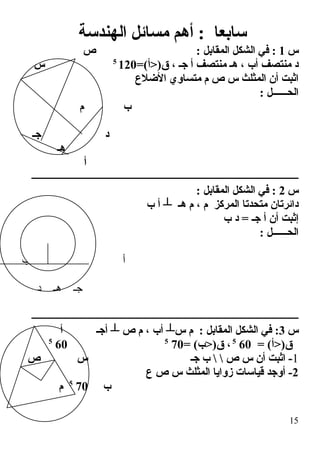
: ‫الهندسة‬ ‫نظريات‬ ‫ملخص‬ : ‫ثالثا‬
1(‫يكون‬ ‫الوتر‬ ‫وبمنتصف‬ ‫الدائرة‬ ‫بمركز‬ ‫المار‬ ‫المستقيم‬‫عليه‬ ‫عمودي‬
2(‫الوتر‬ ‫على‬ ‫عمودي‬ ‫الدائرة‬ ‫بمركز‬ ‫المار‬ ‫المستقيم‬‫الوحتر‬ ‫ينصف‬
3(‫وينصفه‬ ‫الوتر‬ ‫على‬ ‫العمودي‬ ‫المستقيم‬‫الدائرة‬ ‫بمركز‬ ‫يمر‬
1

2. 4(‫يكون‬ ‫المماس‬‫القطر‬ ‫نصف‬ ‫على‬ ‫عمودي‬‫التماس‬ ‫نقطة‬ ‫من‬
5(‫يكون‬ ‫نهايتية‬ ‫احدى‬ ‫من‬ ‫القطر‬ ‫على‬ ‫العمودي‬ ‫المستقيم‬‫للدائرة‬ ‫مماس‬
6(‫يكون‬ ‫متقاطعتين‬ ‫لدائرتين‬ ‫المركزين‬ ‫خط‬‫الوحتر‬ ‫على‬ ‫عمودي‬
‫وينصفه‬ ‫المشترك‬
7(‫يكون‬ ‫متماستين‬ ‫لدائرتين‬ ‫المركزين‬ ‫خط‬‫المماس‬ ‫على‬ ‫عمودي‬
‫المشترك‬‫ويمر‬‫التماس‬ ‫بنقطة‬
8(‫نقطتين‬ ‫أو‬ ‫واحدة‬ ‫بنقطة‬ ‫المارة‬ ‫الدوائر‬ ‫عدد‬‫لنهائي‬ ‫عدد‬ =
‫واحدة‬ ‫استقامة‬ ‫على‬ ‫نقط‬ ‫بثل ث‬ ‫المارة‬ ‫الدوائر‬ ‫عدد‬(‫صفر)ليوجد‬ =
= ‫واحدة‬ ‫استقامة‬ ‫على‬ ‫ليست‬ ‫نقط‬ ‫بثل ث‬ ‫المارة‬ ‫الدوائر‬ ‫عدد‬1
9(‫التي‬ ‫هي‬ ‫للمثلث‬ ‫الخارجة‬ ‫الدائرة‬‫برءوسه‬ ‫حتمر‬
10(‫التي‬ ‫هي‬ ‫للمثلث‬ ‫الداخلة‬ ‫الدائرة‬‫أضلعه‬ ‫جميع‬ ‫حتمس‬
11‫تقاطع‬ ‫نقطة‬ ‫هو‬ ‫للمثلث‬ ‫الخارجة‬ ‫الدائرة‬ ‫(مركز‬‫أضلعه‬ ‫حتماثل‬ ‫محاور‬
12‫تقاطع‬ ‫هونقطة‬ ‫للمثلث‬ ‫الداخلة‬ ‫الدائرة‬ ‫مركز‬ (‫الداخلة‬ ‫زواياه‬ ‫منصفات‬
13(‫على‬ ‫تكون‬ ‫الطول‬ ‫في‬ ‫المتساوية‬ ‫الوتار‬‫المركز‬ ‫من‬ ‫متساوية‬ ‫أبعاد‬
14‫تكون‬ ‫فانها‬ ‫المركز‬ ‫من‬ ‫متساوية‬ ‫أبعاد‬ ‫على‬ ‫الوتار‬ ‫كانت‬ ‫(إذا‬
‫الطول‬ ‫في‬ ‫متساوية‬
15= ‫الدائرة‬ ‫قياس‬ (3605
‫الدائرة‬ ‫محيط‬ = ‫الدائرة‬ ‫طول‬ ،=2‫نق‬ ‫הּ‬
16‫الزاوية‬ ‫قياس‬ = ‫القوس‬ ‫(قياس‬‫له‬ ‫المقابله‬ ‫المركزية‬
17(‫قوسان‬ ‫يحصران‬ ‫المتوازيان‬ ‫الوتران‬‫القياس‬ ‫في‬ ‫متساويان‬
18(‫يوازيه‬ ‫ومماس‬ ‫وتر‬ ‫بين‬ ‫المحصوران‬ ‫القوسان‬‫القياس‬ ‫في‬ ‫متساويان‬
19(‫أوتارها‬ ‫تكون‬ ‫القياس‬ ‫في‬ ‫المتساوية‬ ‫القواس‬‫الطول‬ ‫في‬ ‫متساوية‬
20(‫المحيطية‬ ‫الزاوية‬ ‫قياس‬.‫يساوي‬‫قياس‬ ‫نصف‬‫المشتركة‬ ‫المركزية‬
‫القوس‬ ‫نفس‬ ‫في‬ ‫معها‬( ‫المحيطية‬ ‫ضعف‬ = ‫المركزية‬ )
21(‫المحيطية‬ ‫الزاوية‬ ‫قياس‬.‫يساوي‬‫قياس‬ ‫نصف‬‫لها‬ ‫المقابل‬ ‫القوس‬
22‫تكون‬ ‫دائرة‬ ‫نصف‬ ‫في‬ ‫المرسومة‬ ‫المحيطية‬ ‫(الزاوية‬) ‫قائمة‬=905
(
23(‫تكون‬ ‫القوس‬ ‫نفس‬ ‫تحصر‬ ‫التي‬ ‫المحيطية‬ ‫الزوايا‬‫القياس‬ ‫في‬ ‫متساوية‬
24‫تكونان‬ ‫دائرة‬ ‫خارج‬ ‫نقطة‬ ‫من‬ ‫المرسومتان‬ ‫المماستان‬ ‫القطعتان‬ (
‫الطول‬ ‫في‬ ‫متساويتان‬
2

3. 25‫يكونان‬ ‫قطر‬ ‫نهايتي‬ ‫من‬ ‫المرسومان‬ ‫المماسان‬ (‫متوازيان‬
26‫يكونان‬ ‫وتر‬ ‫نهايتي‬ ‫من‬ ‫المرسومان‬ ‫المماسان‬ (‫متقاطعان‬
27‫يساوي‬ ‫المماسية‬ ‫الزاوية‬ ‫قياس‬ (‫المحيطية‬ ‫الزاوية‬ ‫قياس‬‫المشتركة‬
‫القوس‬ ‫نفس‬ ‫في‬ ‫معها‬
28‫المماسية‬ ‫الزاوية‬ ‫قياس‬ (.‫يساوي‬‫قياس‬ ‫نصف‬‫معها‬ ‫المشتركة‬ ‫المركزية‬
‫القوس‬ ‫نفس‬ ‫في‬‫ضعف‬ = ‫المركزية‬ )‫المماسية‬(
29(‫المماسية‬ ‫الزاوية‬ ‫قياس‬.‫يساوي‬‫قياس‬ ‫نصف‬‫لها‬ ‫المقابل‬ ‫القوس‬
30(‫تساوي‬ ‫بينهما‬ ‫المحصورة‬ ‫الزاوية‬ ‫وكان‬ ‫وتر‬ ‫نهاية‬ ‫من‬ ‫شعاع‬ ‫رسم‬ ‫إذا‬
‫الشعاع‬ ‫هذا‬ ‫كان‬ ‫المحيطية‬ ‫الزاوية‬‫للدائرة‬ ‫مماس‬.
31(‫المركزين‬ ‫خط‬ ‫يسمى‬ ‫ن‬ ‫م‬ : ‫أخرى‬ ‫لدائرة‬ ‫بالنسبة‬ ‫دائرة‬ ‫موضع‬
‫نق‬ = ‫المجموع‬1‫نق‬ +2‫نق‬ = ‫الفرق‬ ،1‫نق‬ –2
‫الدائرحتان‬ ‫حتكون‬1‫المجموع‬ = ‫ن‬ ‫م‬ ‫كان‬ ‫اذا‬ ‫الخارج‬ ‫من‬ ‫متماستان‬ -
2، ‫الفرق‬ = ‫ن‬ ‫م‬ ‫الداخل‬ ‫من‬ ‫متماستان‬ -3‫المجموع‬ < ‫ن‬ ‫م‬ ‫متباعدحتان‬ -
4، ‫الفرق‬ > ‫ن‬ ‫م‬ ‫متداخلتان‬ -5‫والمجموع‬ ‫الفرق‬ ‫بين‬ ‫ن‬ ‫م‬ ‫متقاطعتان‬ -
6‫صفر‬ = ‫ن‬ ‫م‬ ‫كان‬ ‫اذا‬ ‫المركز‬ ‫متحدحتا‬ -
32(‫دائري‬ ‫رباعي‬ ‫الشكل‬ ‫فيها‬ ‫يكون‬ ‫التي‬ ‫الحالت‬
1‫منها‬ ‫واحدة‬ ‫جهة‬ ‫وفي‬ ‫واحدة‬ ‫قاعدة‬ ‫على‬ ‫مرسومتان‬ ‫زاويتان‬ ‫تساوى‬ ‫اذا‬ -
2‫متقابلتان‬ ‫زاويتان‬ ‫بالشكل‬ ‫وجد‬ ‫-إذا‬‫متكاملتان‬‫مجموعهم‬ )1805
(
3‫الزاوية‬ ‫يساوي‬ ‫الخارجة‬ ‫الزاوية‬ ‫قياس‬ ‫كان‬ ‫إذا‬ -
‫لها‬ ‫للمجاورة‬ ‫المقابلة‬ ‫الداخلة‬
4‫رءوسه‬ ‫عن‬ ‫ثابت‬ ‫بعد‬ ‫تبعد‬ ‫الشكل‬ ‫مستوى‬ ‫في‬ ‫نقطة‬ ‫وجدت‬ ‫-إذا‬
33= ‫متباعدحتان‬ ‫لدانرحتان‬ ‫المشتركة‬ ‫المماسات‬ ‫عدد‬ –4= ‫،متقاطعتان‬2
= ‫الخارج‬ ‫من‬ ‫متماستان‬3= ‫الداخل‬ ‫من‬ ‫متماستان‬ ،1
(‫صفر)ليوجد‬ =( ‫المركز‬ ‫متحدحتا‬ ) ‫متداخلتان‬
34‫حتقع‬ ‫أ‬ ‫فإن‬ ‫نق‬ > ‫أ‬ ‫م‬ ، ‫الدائرة‬ ‫خارج‬ ‫حتقع‬ ‫أ‬ ‫فإن‬ ‫نق‬ < ‫أ‬ ‫م‬ ‫كان‬ ‫إذا‬ –
‫الدائرة‬ ‫على‬ ‫حتقع‬ ‫أ‬ ‫فإن‬ ‫نق‬ = ‫أ‬ ‫م‬ ‫كان‬ ‫إذا‬ ، ‫الدائرة‬ ‫داخل‬
35= ‫دائرة‬ ‫ربع‬ ‫في‬ ‫المرسومة‬ ‫المحيطية‬ ‫الزاوية‬ ‫قياس‬ -1355
3

4. ‫الهندسة‬ ‫نظريات‬ ‫اثبات‬ : ‫رابعا‬
1(‫متساوية‬ ‫أبعاد‬ ‫على‬ ‫حتكون‬ ‫الطول‬ ‫في‬ ‫المتساوية‬ ‫الوحتار‬ ) ‫أن‬ ‫اثبت‬
‫جـ‬ ‫أ‬ ( ‫مركزها‬ ‫من‬
‫م‬ ‫ص‬ ‫جـ‬ ، ‫م‬ ‫س‬ ‫أ‬ ‫المثلثان‬ ‫بتطابق‬ : ‫البرهان‬
‫أص‬ = ‫أس‬ ‫فيهما‬
‫جـ‬ ‫م‬ = ‫أ‬ ‫م‬
= (‫ص‬ > )‫ق‬ = (‫س‬ >)‫ق‬905
‫ا‬ً ‫إذ‬‫ب‬ ‫ص‬ ‫م‬ = ‫س‬ ‫م‬ ‫أن‬ ‫وينتج‬ ‫المثلثان‬ ‫يتطابق‬
‫د‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
2) ‫أن‬ ‫اثبت‬ (‫المحيطية‬ ‫الزاوية‬ ‫قياس‬.‫يساوي‬‫قياس‬ ‫نصف‬‫المركزية‬
‫القوس‬ ‫نفس‬ ‫في‬ ‫معها‬ ‫المشتركة‬‫ج‬ (
‫نق‬ = ‫جـ‬ ‫م‬ = ‫أ‬ ‫م‬ : ‫البرهان‬
( ‫جـ‬ > ) ‫ق‬ = (‫أ‬ >)‫ق‬
( ‫جـ‬ > ) ‫ق‬ + (‫أ‬ >)‫ق‬ = ‫الخارجه‬ ( ‫ب‬ ‫م‬ ‫أ‬ >)‫ق‬
( ‫ب‬ ‫م‬ ‫أ‬ >) ‫نصف‬ = ( ‫جـ‬ > ) ‫ق‬ ‫ا‬ً ‫إذ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
3‫أن‬ ‫اثبت‬ (‫القوس‬ ‫تحصرنفس‬ ‫التي‬ ‫المحيطية‬ ‫الزوايا‬ )‫في‬ ‫متساوية‬
‫القياس‬(
= (‫أ‬ >)‫ق‬ ‫أن‬ ‫بما‬ ‫البرهان‬1‫جـ‬ ‫ب‬ ‫أ‬ ( ‫ص‬ ‫س‬ )‫ق‬
2
= (‫ب‬ >)‫ق‬1(‫ص‬ ‫س‬ )‫ق‬
2
= (‫ق)>جـ‬1(‫ص‬ ‫س‬ )‫ق‬
2‫ص‬ ‫س‬
(‫ق)>جـ‬ = (‫ب‬ >)‫ق‬ = (‫أ‬ >)‫ق‬ ‫ا‬ً ‫إذ‬
4

5. ‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
4‫متكاملتان‬ ‫متقابلتان‬ ‫زاويتان‬ ‫كل‬ ‫الدائري‬ ‫الرباعي‬ ‫الشكل‬ ‫في‬ ‫أنه‬ ‫اثبت‬ (
‫أ‬ ‫أن‬ ‫بما‬ : ‫البرهان‬
= (‫أ‬ >)‫ق‬1(‫د‬ ‫جـ‬ ‫ب‬ ) ‫ق‬
2‫ب‬‫د‬
= (‫ق)>جـ‬1) (‫د‬ ‫أ‬ ‫ب‬ )‫ق‬2(
2
‫بجمع‬1،2‫أن‬ ‫ينتج‬‫جـ‬
= ‫الدائرة‬ ‫قياس‬ ‫نصف‬ = (‫ق)>جـ‬ + (‫أ‬ >)‫ق‬1805
= (‫ق)>د‬ + (‫ب‬ >)‫ق‬ ‫وبالمثل‬1805
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
5) ‫أن‬ ‫اثبت‬ (‫دائرة‬ ‫خارج‬ ‫نقطة‬ ‫من‬ ‫المرسومتان‬ ‫المماستان‬ ‫القطعتان‬
‫تكونان‬( ‫الطول‬ ‫في‬ ‫متساويتان‬
‫م‬ ‫جـ‬ ‫أ‬ ، ‫م‬ ‫ب‬ ‫أ‬ ‫المثلثان‬ ‫بتطابق‬ : ‫البرهان‬
‫جـ‬ ‫م‬ = ‫ب‬ ‫م‬ ‫فيهما‬
‫مشترك‬ ‫ضلع‬ ‫م‬ ‫أ‬
= ( ‫جـ‬ > )‫ق‬ = (‫ب‬ > )‫ق‬905
‫ا‬ً ‫إذ‬‫جـ‬ ‫أ‬ = ‫ب‬ ‫أ‬ ‫أن‬ ‫وينتج‬ ‫المثلثان‬ ‫يتطابق‬ :
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
6‫المحيطية‬ ‫الزاوية‬ ‫قياس‬ ‫يساوي‬ ‫المماسية‬ ‫الزاوية‬ ‫قياس‬ ‫أن‬ ‫ثبت‬ ‫ا‬ (
‫القوس‬ ‫نفس‬ ‫في‬ ‫معها‬ ‫المشتركة‬
= (‫د‬ >)‫ق‬ ‫أن‬ ‫بما‬ :‫البرهان‬1) (‫أب‬ )‫ق‬1‫ب‬ (
2‫د‬
= ( ‫جـ‬ ‫أ‬ ‫ب‬ > )‫ق‬1) (‫أب‬ )‫ق‬2(
2‫أ‬ ‫جـ‬
‫من‬1،2( ‫جـ‬ ‫أ‬ ‫ب‬ )‫ق‬ = (‫د‬ >)‫ق‬ ‫أن‬ ‫ينتج‬
5

6. ‫الجبر‬ ‫مسائل‬ ‫أهم‬ : ‫خامسا‬
‫س‬1‫المعادلتين‬ ‫تحل‬ ‫مجموعة‬ ‫أوجد‬ :2= ‫ص‬ + ‫س‬7= ‫ص‬ – ‫س‬ ،1
‫؟‬ ‫وبيانيا‬ ‫جبريا‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2= ‫ص‬ – ‫س‬ ‫المعادلتين‬ ‫تحل‬ ‫مجموعة‬ ‫أوجد‬ :2،2+ ‫س‬3= ‫ص‬9
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫الصغرى‬ ‫أمثال‬ ‫سبعة‬ ‫يساوي‬ ‫أكبرهما‬ ‫ضعف‬ ‫متكاملتان‬ ‫زاويتان‬ :
‫منهما‬ ‫كل‬ ‫قياس‬ ‫أوجد‬
‫س‬4‫مجموعهما‬ ‫رقمين‬ ‫من‬ ‫مكون‬ ‫عدد‬ :11‫الرقمين‬ ‫وضع‬ ‫عكس‬ ‫واذا‬
‫بمقدار‬ ‫الصلي‬ ‫العدد‬ ‫عن‬ ‫يزيد‬ ‫الناحتج‬ ‫العدد‬ ‫فإن‬27‫الصلي‬ ‫العدد‬ ‫فماهو‬
6

7. ‫س‬5:+ ‫ص‬ ‫المعادلتين‬ ‫تحل‬ ‫مجموعة‬ ‫أوجد‬2= ‫س‬7
،2‫س‬2
+ ‫س‬ +3= ‫ص‬19
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬6:= ‫ص‬ + ‫س‬ ‫المعادلتين‬ ‫تحل‬ ‫مجموعة‬ ‫أوجد‬5،
‫س‬2
‫ص‬ +2
= ‫ص‬ ‫س‬ +19
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬6‫مجموعهما‬ ‫عددان‬ :7‫مربعيهما‬ ‫ومجموع‬25‫العددين‬ ‫أوجد‬
‫س‬7‫قطريه‬ ‫بين‬ ‫الفرق‬ ‫معين‬ :4‫ومحيطه‬ ‫سم‬40‫مساتحته‬ ‫أوجد‬ ‫سم‬
7

8. ‫س‬8‫عرضة‬ ‫عن‬ ‫يزيد‬ ‫طوله‬ ‫مستطيل‬ :5‫ومحيطه‬ ‫سم‬18‫أوجد‬ ‫سم‬
‫مساتحته‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬9‫محيطة‬ ‫مستطيل‬ :28‫ومساتحته‬ ‫سم‬40‫سم‬2
‫بعديه‬ ‫أوجد‬
‫س‬10‫وتحاصل‬ ‫عشراحته‬ ‫رقم‬ ‫ضعف‬ ‫اتحاده‬ ‫رقم‬ ، ‫رقمين‬ ‫من‬ ‫مكون‬ ‫عدد‬ :
‫العدد‬ ‫هو‬ ‫فما‬ ‫الصلي‬ ‫العدد‬ ‫نصف‬ = ‫الرقمين‬ ‫ضرب‬
‫س‬11‫المستقيم‬ ‫على‬ ‫نقطه‬ ‫حتتحرك‬ :5– ‫س‬2= ‫ص‬1‫كان‬ ‫بحيث‬
‫النقطه‬ ‫هذه‬ ‫اتحداثي‬ ‫أوجد‬ ‫السيني‬ ‫اتحداثيها‬ ‫مربع‬ ‫ضعف‬ ‫الصادي‬ ‫اتحداثيها‬
8

9. ‫س‬12‫المعادلة‬ ‫حل‬ ‫العام‬ ‫القانون‬ ‫باستخدام‬ :2‫س‬2
-4+ ‫س‬1=0
. ‫عشرية‬ ‫أرقام‬ ‫ةثلةثة‬ ‫لقرب‬
‫س‬13- ‫س‬ ) ‫س‬ ‫المعادلة‬ ‫حل‬ ‫العام‬ ‫القانون‬ ‫باستخدام‬ :1= (4‫لقرب‬
. ‫عشريين‬ ‫رقمين‬
‫س‬14=( ‫د)س‬ ‫للدالة‬ ‫البياني‬ ‫الشكل‬ ‫:ارسم‬1‫س‬ –2
-] ‫الفترة‬ ‫في‬2،2‫أوجد‬ ‫الرسم‬ ‫ومن‬ [
: ‫المنحنى‬ ‫رأس‬............
:‫التماةثل‬ ‫معادلة‬...........
: ‫العظمى‬ ‫القيمة‬.........
‫س‬ ‫المعادلة‬ ‫حل‬ ‫مجموعة‬2
–4=0
............................. :
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬15‫س‬ = ( ‫د)س‬ ‫للدالة‬ ‫البياني‬ ‫الشكل‬ ‫ارسم‬ :2
–4+ ‫س‬3‫في‬
-] ‫الفترة‬1،5‫أوجد‬ ‫الرسم‬ ‫ومن‬ [
: ‫المنحنى‬ ‫رأس‬............
:‫التماةثل‬ ‫معادلة‬...........
: ‫العظمى‬ ‫القيمة‬.........
=(‫د)س‬ ‫المعادلة‬ ‫جذري‬0
9

10. ‫س‬16: ‫يأتي‬ ‫ما‬ ‫كمل‬ ‫أ‬ :
1‫س‬ = (‫د)س‬ ‫الدالة‬ ‫أصفار‬ ‫مجموعة‬ -2
–9................ ‫هي‬
2‫س‬ = (‫د)س‬ ‫الدالة‬ ‫أصفار‬ ‫مجموعة‬ -2
+9................ ‫هي‬
3= (‫د)س‬ ‫الدالة‬ ‫أصفار‬ ‫مجموعة‬ -7................ ‫هي‬
4................ ‫هي‬ ‫صفر‬ = (‫د)س‬ ‫الدالة‬ ‫أصفار‬ ‫مجموعة‬ -
5+ ‫س‬ = (‫س‬ ) ‫د‬ ‫الدالة‬ ‫مجال‬ -5-‫س‬ +2........... ‫هو‬
+ ‫س‬3- ‫س‬7
6‫الجبري‬ ‫الكسر‬ ‫كان‬ ‫اذا‬ -2......... ‫مجاله‬ ‫فإن‬ ‫ضربي‬ ‫معكوس‬ ‫له‬ ‫س‬
– ‫س‬3
7– ‫س‬ = (‫د)س‬ -5............. = ‫س‬ ‫عندما‬ ‫وجود‬ ‫لها‬ ‫ليس‬
– ‫س‬3
8+ ‫س‬ ‫الجبري‬ ‫للكسر‬ ‫الجمعي‬ ‫المعكوس‬ ‫مجال‬ -3................. ‫هو‬
+ ‫س‬2
9– ‫س‬ = (‫ن)س‬ -2‫ن‬ ‫مجال‬ ‫فان‬-1
............... ‫هو‬ ( ‫س‬ )
3‫س‬
10+ ‫س‬ ‫المعادلتان‬ ‫كان‬ ‫اذا‬ -4= ‫ص‬7،3= ‫ص‬ ‫ك‬ + ‫س‬21‫لهما‬
............. = ‫ك‬ ‫فإن‬ ‫الحلول‬ ‫من‬ ‫نهائي‬ ‫ل‬ ‫عدد‬
11= ‫ص‬ ‫المستقيمان‬ ‫تقاطع‬ ‫نقطة‬ -2= ‫ص‬ + ‫س‬ ،6.......... ‫هي‬
12‫ب‬ ‫كان‬ ‫اذا‬ -2
–4< ‫جـ‬ ‫أ‬0.......... = ‫ور‬ ‫الجذ‬ ‫عدد‬ ‫فإن‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬17+ ‫ب‬ = (‫س‬ ) ‫ن‬ ‫الدالة‬ ‫مجال‬ ‫كان‬ ‫اذا‬ :9} – ‫ح‬ ‫هو‬0،4{
‫أ‬ + ‫س‬ ‫س‬
) ‫ن‬ ،5= (2‫ب‬ ، ‫أ‬ ‫قيمة‬ ‫أوجد‬
10

11. ‫س‬18‫ن‬ :1‫س‬ =(‫)س‬2
‫ن‬ ،2‫س‬ =(‫)س‬3
‫س‬ +2
‫س‬ +
‫س‬3
‫س‬ –2
‫س‬4
‫س‬ –
‫ن‬ ‫أن‬ ‫إةثبت‬1‫ن‬ =2
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬19‫ن‬ :– ‫س‬ =(‫)س‬6-‫س‬ +5
2‫س‬2
–15+ ‫س‬1815–13+ ‫س‬2‫س‬2
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬20‫ن‬ :‫س‬ =(‫)س‬2
+2+ ‫س‬4-9‫س‬ –2
‫س‬3
-8‫س‬2
– ‫س‬ +6
11

12. ‫س‬21‫ن‬ :‫س‬ =(‫)س‬3
–1×2– ‫س‬2
‫س‬2
–2+ ‫س‬1‫س‬2
+ ‫+س‬1
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬22:‫ن‬‫س‬ =(‫)س‬2
–9÷3‫س‬2
+6- ‫س‬15
2‫س‬2+3‫س‬4‫س‬2
-9
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬23‫ن‬ :‫س‬ =(‫)س‬3
+3‫س‬2
+2‫ن‬ ‫أوجد‬ ‫س‬-1
،‫ومجاله‬ (‫)س‬
‫س‬2
+2‫ن‬ ‫س‬-1
)2‫ن‬ ، (-1
- )2(
12

13. ‫الحتمال‬ ‫مسائل‬ ‫أهم‬ : ‫سادسا‬
‫س‬1‫على‬ ‫يحتوي‬ ‫صندوق‬ :12، ‫كرة‬5، ‫زرقاء‬4‫والباقي‬ ، ‫حمراء‬
: ‫تكون‬ ‫أن‬ ‫احتمال‬ ‫أوجد‬ ‫عشوائيا‬ ‫كرة‬ ‫سحبت‬ ‫بيضاء‬
1-‫زرقاء‬
2-‫حمراء‬ ‫ليست‬
3-‫حمراء‬ ‫أو‬ ‫زرقاء‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫من‬ ‫بطاقة‬ ‫:سحبت‬20‫من‬ ‫مرقمة‬ ‫بطاقة‬1:20‫عدد‬ ‫احتمال‬ ‫أوجد‬
1-‫على‬ ‫القسمة‬ ‫يقبل‬3
2-‫للعدد‬ ‫مضاعف‬5
3-‫على‬ ‫القسمة‬ ‫يقبل‬3،5
4-‫عف‬ ‫مضا‬3‫أو‬5
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3= (‫ل)أ‬ ‫كان‬ ‫إذا‬ :0.5= (‫ب‬ )‫ل‬ ،0.6= (‫∩ب‬ ‫ل)أ‬ ،0.3‫أوجد‬
1‫أ‬ )‫ل‬ -U= (‫ب‬
2= ( ‫ب‬ - ‫)أ‬ ‫ل‬ -
3‫أ‬ )‫ل‬ -
= (
4‫ب‬ )‫ل‬
= (
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬4= (‫ل)أ‬ ‫كان‬ ‫إذا‬ :0.4= (‫ب‬ )‫ل‬ ،0.3‫أ‬ )‫ل‬ ‫أوجد‬U‫الحال ت‬ ‫في‬ (‫ب‬
‫التية‬1، ‫متنافيان‬ ‫حدةثان‬ ‫،ب‬ ‫أ‬ -2= (‫∩ب‬ ‫ل)أ‬ -0.2
13

14. ‫س‬5= (‫)ب‬ ‫ل‬ ‫كان‬ ‫إذا‬ :0.2‫أ‬ )‫ل‬ ،U= (‫ب‬0.8‫كان‬ ‫إذا‬ (‫ل)أ‬ ‫أوجد‬
1-‫متنافيان‬ ‫حدةثان‬ ‫،ب‬ ‫أ‬
2-‫ب‬‫כ‬‫أ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬6‫أ‬ )‫ل‬ ‫كان‬ ‫إذا‬ :U= (‫ب‬5= (‫ل)ب‬ ،5‫النواتج‬ ‫عدد‬ ‫وكان‬
612
‫يساوي‬ ‫أ‬ ‫الحدث‬ ‫وقوع‬ ‫الى‬ ‫تؤدي‬ ‫التي‬13‫الممكنة‬ ‫النواتج‬ ‫جميع‬ ‫وعدد‬
24‫أوجد‬1. ‫أ‬ ‫الحدث‬ ‫وقوع‬ ‫احتمال‬ -
2. ‫معا‬ ‫ب‬ ‫و‬ ‫أ‬ ‫الحدةثين‬ ‫وقوع‬ ‫احتمال‬ -
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬7‫أوجد‬ ‫المقابل‬ ‫فن‬ ‫شكل‬ ‫باستخدام‬ :
‫ف‬ =(‫∩ب‬ ‫ل)أ‬
‫أ‬ )‫ل‬U=(‫ب‬12
=( ‫ب‬ - ‫)أ‬ ‫ل‬3456
‫أ‬ )‫ل‬
=(
= ( ‫ف‬ )‫ل‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬8‫به‬ ‫فصل‬ :40‫منهم‬ ‫طالب‬18‫و‬ ‫الهرام‬ ‫يقرأون‬15‫يقرأون‬
‫و‬ ‫البخبار‬8‫احتمال‬ ‫أوجد‬ ‫عشوائيا‬ ‫تلميذ‬ ‫أبختير‬ ‫معا‬ ‫الجريدتين‬ ‫يقرأون‬
1‫الهرام‬ ‫يقرأ‬ -
2‫البخبار‬ ‫يقرأ‬ -
3‫معا‬ ‫البخبار‬ ‫و‬ ‫الهرام‬ ‫يقرأ‬ -
4‫البخبار‬ ‫أو‬ ‫الهرام‬ ‫يقرأ‬ -
5--‫الهرام‬ ‫يقرأ‬.‫فقط‬
14

15. ‫الهندسة‬ ‫مسائل‬ ‫أهم‬ : ‫سابعا‬
‫س‬1‫ص‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
=(‫ق)>أ‬ ، ‫جـ‬ ‫أ‬ ‫منتصف‬ ‫هـ‬ ، ‫أب‬ ‫منتصف‬ ‫د‬1205
‫س‬
‫الضلع‬ ‫متساوي‬ ‫م‬ ‫ص‬ ‫س‬ ‫المثلث‬ ‫أن‬ ‫اةثبت‬
: ‫الحــــــل‬
‫م‬ ‫ب‬
‫د‬‫جـ‬
‫هـ‬
‫أ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2: ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫ب‬ ‫أ‬ ┴ ‫هـ‬ ‫م‬ ، ‫م‬ ‫المركز‬ ‫متحدتا‬ ‫دائرتان‬
‫ب‬ ‫د‬ = ‫جـ‬ ‫أ‬ ‫أن‬ ‫إةثبت‬
‫م‬ : ‫الحــــــل‬
‫أ‬‫ب‬
‫د‬ ‫هـ‬ ‫جـ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫أ‬ ‫أجـ‬ ┴ ‫ص‬ ‫م‬ ، ‫أب‬ ┴‫س‬ ‫م‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
= (‫ق)>أ‬605
= (‫ق)>ب‬ ،705
605
1‫جـ‬ ‫ب‬ ‫ص‬ ‫س‬ ‫أن‬ ‫اةثبت‬ -‫ص‬ ‫س‬
2‫ع‬ ‫ص‬ ‫س‬ ‫المثلث‬ ‫زوايا‬ ‫قياسا ت‬ ‫أوجد‬ -
‫ب‬705
‫م‬
15

16. ‫جـ‬
‫س‬4: ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫ب‬
= (‫ق)>ب‬ ، ‫مماس‬ ‫أب‬505
‫جـ‬ ‫د‬ ‫جـ‬ ‫منتصف‬ ‫هـ‬ ،
1-‫هـ‬ ‫دائري‬ ‫رباعي‬ ‫ب‬ ‫هـ‬ ‫م‬ ‫أ‬ ‫الشكل‬ ‫أن‬ ‫اةثبت‬
2-( ‫هـ‬ ‫م‬ ‫أ‬ >)‫ق‬ ‫أوجد‬
‫أ‬ ‫م‬ ‫د‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬5:‫للدائرة‬ ‫مماس‬ ‫س‬ ‫م‬ ‫أن‬ ‫إةثبت‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬
‫م‬ ‫ع‬
8‫سم‬5‫سم‬
‫ص‬12‫س‬ ‫سم‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬6:‫المقابل‬ ‫الشكل‬ ‫في‬:‫مماس‬ ‫ب‬ ‫أ‬،)‫ق‬=(‫ب‬5
30
= ‫م‬ ‫أ‬8‫ب‬ ‫م‬ ┴ ‫جـ‬ ‫أ‬ ، ‫سم‬
‫أجـ‬ ، ‫ب‬ ‫أ‬ ، ‫ب‬ ‫م‬ ‫طول‬ ‫أوجد‬
‫م‬
8‫سم‬‫جـ‬
5
30
16

17. ‫ب‬ ‫أ‬
‫س‬7‫قطريهما‬ ‫نصفي‬ ‫ن‬ ، ‫م‬ ‫دائرتان‬ :3، ‫سم‬8‫موضع‬ ‫بين‬ ‫سم‬
‫كان‬ ‫اذا‬ ‫للرخرى‬ ‫بالنسبة‬ ‫الدائرتان‬
1= ‫ن‬ ‫م‬ (8‫سم‬2= ‫ن‬ ‫م‬ (5‫سم‬
3= ‫ن‬ ‫م‬ (9‫سم‬4= ‫ن‬ ‫م‬ (4‫سم‬
5= ‫ن‬ ‫م‬ (7‫سم‬6‫صفر‬ = ‫ن‬ ‫م‬ (
7......................... ‫ن‬ ‫م‬ ‫فإن‬ ‫متقاطعتان‬ ‫الدائرتان‬ ‫كانت‬ ‫أذا‬ (
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬8‫جـ‬ ‫دائرتان‬ ‫ن‬ ، ‫م‬ ‫المقابل‬ ‫الشكل‬ ‫في‬ :
= (‫ق)>جـ‬ ‫ب‬ ، ‫أ‬ ‫في‬ ‫متقاطعتان‬555
55
= (‫ق)>ن‬1255
‫أ‬ ‫مماس‬ ‫د‬ ‫جـ‬ ‫أن‬ ‫إثبت‬
‫د‬
125
‫م‬
‫ن‬
‫ب‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬9‫المقابل‬ ‫الشكل‬ ‫في‬ ::‫ب‬ ، ‫أ‬ ‫في‬ ‫متقاطعتان‬ ‫دائرتان‬ ‫ن‬ ، ‫م‬
‫هـ‬ (‫ق)>هـ‬ = ( ‫ن‬ ‫م‬ ‫د‬ >)‫ق‬ ‫أن‬ ‫اثبت‬ ، ‫مماس‬ ‫هـ‬ ‫جـ‬
‫أ‬ ‫جـ‬
‫ن‬ ‫و‬ ‫م‬
17

18. ‫ب‬ ‫د‬
‫س‬10= ‫ب‬ ‫أ‬ ‫ارسم‬ ‫الهندسية‬ ‫الدوات‬ ‫باستخدام‬ :4‫دائرة‬ ‫ارسم‬ ‫ثم‬ ‫سم‬
‫قطرها‬ ‫وطول‬ ‫ب‬ ، ‫أ‬ ‫بالنقطتين‬ ‫تمر‬5‫الممكنة‬ ‫الحلول‬ ‫عدد‬ ‫كم‬ ‫سم‬
‫س‬11‫المتساوي‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫ارسم‬ ‫الهندسية‬ ‫الدوات‬ ‫باستخدام‬ :
‫ضلعه‬ ‫طول‬ ‫والذي‬ ‫الضل ع‬4‫له‬ ‫الخارجة‬ ‫الدائرة‬ ‫ارسم‬ ‫ثم‬ ‫سم‬
18

19. ‫س‬12= ‫أب‬ ، ‫ب‬ ‫في‬ ‫القائم‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫ارسم‬ :3= ‫جـ‬ ‫ب‬ ، ‫سم‬4‫سم‬
‫؟‬ ‫قطرها‬ ‫نصف‬ ‫طول‬ ‫وأوجد‬ ‫له‬ ‫الخارجة‬ ‫الدائرة‬ ‫ارسم‬ ‫ثم‬
‫س‬13‫جـ‬ ‫أ‬ ‫منتصف‬ ‫ص‬ ، ‫ب‬ ‫أ‬ ‫منتصف‬ ‫س‬ ، ‫متساويان‬ ‫وتران‬ ‫أجـ‬ ، ‫:أب‬
‫أن‬ ‫اثبت‬1‫أ‬ ‫هـ‬ ‫ص‬ = ‫د‬ ‫س‬ -
2‫هـ‬ ‫د‬ ( ‫جـ‬ ‫ص‬ ‫(=ق)>س‬ ‫ب‬ ‫س‬ ‫ص‬ >)‫ق‬ -
‫ص‬ ‫س‬
‫م‬
‫جـ‬ ‫ب‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬14‫م‬ ‫دائرة‬ ‫في‬ ‫وتران‬ ‫أجـ‬ ، ‫أب‬ :‫جـ‬ ‫أ‬ ‫منتصف‬ ‫ص‬ ، ‫ب‬ ‫أ‬ ‫منتصف‬ ‫س‬
= ( ‫جـ‬ ‫ب‬ ‫ق)>أ‬755
‫ص‬ ‫م‬ = ‫س‬ ‫م‬ ،1( ‫جـ‬ ‫أ‬ ‫ب‬ > ) ٌ ‫أوجد‬ -
2‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫محيط‬ ‫نصف‬ = ‫ص‬ ‫س‬ ‫أ‬ ‫المثلث‬ ‫محيط‬ ‫أن‬ ‫اثبت‬ -
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫جـ‬ ‫أ‬
‫س‬15‫جـ‬ ‫┴أ‬ ‫ص‬ ‫م‬ ، ‫ب‬ ‫┴أ‬ ‫س‬ ‫:م‬ ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫هـ‬ ‫و‬ ‫هـ‬ ‫جـ‬ = ‫أو‬ ، ‫أجـ‬ = ‫أب‬ ‫أن‬ ‫اثبت‬ ‫هـ‬ ‫ص‬ = ‫وس‬
‫ص‬ ‫م‬ ‫س‬
19

20. ‫جـ‬ ‫ب‬
‫س‬16= ( ‫د‬ ‫م‬ ‫جـ‬ >)‫ق‬ ، ‫قطر‬ ‫اب‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :705
= (‫ب‬ ‫ق)د‬ : ( ‫جـ‬ ‫ق)أ‬5:6‫د‬ ‫جـ‬ ( ‫د‬ ‫جـ‬ ‫أ‬ )‫ق‬ ‫أوجد‬
‫أ‬70
‫ب‬
‫م‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬17‫د‬ ‫جـ‬ // ‫و‬ ‫هـ‬ // ‫أب‬ ، ‫مماس‬ ‫د‬ ‫جـ‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫و‬ ‫جـ‬ = ‫هـ‬ ‫جـ‬ ‫أن‬ ‫اثبت‬
‫و‬ ‫هـ‬
‫ب‬ ‫أ‬
‫د‬ ‫جـ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬18‫دائرة‬ ‫دارخل‬ ‫مرسوم‬ ‫مستطيل‬ ‫د‬ ‫جـ‬ ‫أب‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫جـ‬ ‫ب‬ = ‫هـ‬ ‫أ‬ ‫أن‬ ‫اثبت‬ ‫د‬ ‫جـ‬ = ‫هـ‬ ‫جـ‬
‫د‬ ‫أ‬
‫جـ‬ ‫ب‬
20

21. ‫هـ‬
‫س‬19= (‫ق)>م‬ ‫ب‬ ‫أ‬ // ‫د‬ ‫جـ‬ ‫مماس‬ ‫د‬ ‫جـ‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :1205
‫د‬ ‫جـ‬ ‫الضل ع‬ ‫متساوي‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫أن‬ ‫اثبت‬
‫م‬
‫ب‬ ‫أ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬20‫في‬ ‫الدائرة‬ ‫قطع‬ ‫م‬ ‫أ‬ ، ‫ب‬ ‫عند‬ ‫مماس‬ ‫ب‬ ‫أ‬ ‫م‬ ‫الدائرة‬ ‫رخارج‬ ‫نقطة‬ ‫أ‬ :
= ( ‫أ‬ > )‫ق‬ ، ‫الترتيب‬ ‫على‬ ‫د‬ ، ‫جـ‬40( ‫جـ‬ ‫د‬ ‫ب‬ >)‫ق‬ ‫أوجد‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬21‫ب‬ ‫أ‬ // ‫م‬ ‫جـ‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫هـ‬ ‫أ‬ < ‫هـ‬ ‫ب‬ ‫أن‬ ‫اثبت‬
‫م‬ ‫جـ‬
‫هـ‬
‫ب‬ ‫أ‬
21

22. ‫س‬22:: ‫المقابل‬ ‫الشكل‬ ‫في‬
= ( ‫د‬ ‫أ‬ )‫ق‬505
= ( ‫ب‬ ‫جـ‬ )‫ق‬ ،705
‫جـ‬ ‫أ‬
( ‫جـ‬ ‫هـ‬ ‫أ‬ > )‫ق‬ ، ( ‫د‬ ‫هـ‬ ‫أ‬ > )‫ق‬ ‫أوجد‬
‫هـ‬
‫ب‬ ‫د‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬23: ‫المقابل‬ ‫الشكل‬ ‫في‬ :
= ( ‫د‬ ‫أ‬ )‫ق‬305
= ( ‫ب‬ ‫جـ‬ )‫ق‬ ،705
‫ب‬ ‫أ‬
‫هـ‬
‫جـ‬ ‫د‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬24: ‫المقابل‬ ‫الشكل‬ ‫في‬ :
= ( ‫ق)>أ‬405
= ( ‫د‬ ‫ق)ب‬ ،605
( ‫ب‬ ‫جـ‬ )‫ق‬=( ‫هـ‬ ‫د‬ )‫ق‬‫جـ‬ ‫ب‬
‫أوجد‬‫أ‬ ( ‫ب‬ ‫جـ‬ )‫ق‬ ، ( ‫هـ‬ ‫جـ‬ )‫ق‬40
40‫د‬
‫هـ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬25:= ( ‫ق)>أ‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬305
=( ‫د‬ ‫ق)ب‬445
‫جـ‬ ‫ق)>د‬ ،
= ( ‫هـ‬485
‫هـ‬ ( ‫جـ‬ ‫ب‬ ) ‫ق‬ ، ( ‫هـ‬ ‫جـ‬ ) ‫ق‬ ‫أوجد‬
‫د‬
22

23. ‫أ‬‫و‬
‫ب‬
‫جـ‬
‫س‬26‫جـ‬ : ‫المقابل‬ ‫الشكل‬ ‫:في‬
= ( ‫جـ‬ ‫ب‬ ‫أ‬ > )‫ق‬ ‫قطر‬ ‫ب‬ ‫أ‬655
(‫و‬ > )‫ق‬ ‫أوجد‬
65
‫ب‬ ‫أ‬
‫و‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬27‫جـ‬ ‫ب‬ // ‫هـ‬ ‫د‬ : ‫المقابل‬ ‫الشكل‬ ‫:في‬
‫أ‬ (‫ب‬ ‫أ‬ ‫هـ‬ > )‫ق‬ – ( ‫جـ‬ ‫أ‬ ‫ق)>د‬ ‫أن‬ ‫اثبت‬
‫هـ‬ ‫د‬
‫جـ‬ ‫ب‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬28‫المقابل‬ ‫الشكل‬ ‫:في‬:‫د‬ ‫هـ‬ = ‫هـ‬ ‫أ‬
‫د‬ ‫أ‬ ‫جـ‬ ‫هـ‬ = ‫ب‬ ‫هـ‬ ‫أن‬ ‫اثبت‬
‫هـ‬
‫ب‬ ‫جـ‬
23

24. ‫س‬29‫جـ‬ ‫د‬ ‫د‬ ‫أ‬ = ‫ب‬ ‫أ‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
= (‫ق)>أ‬80= (‫ق)>ب‬ ،50‫أن‬ ‫اثبت‬50
‫واحدة‬ ‫دائرة‬ ‫تمربها‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫النقط‬
‫ب‬ ‫أ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬30‫ب‬ > ‫ينصف‬ ‫س‬ ‫،ب‬ ‫أجـ‬ = ‫أب‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫أ‬ ‫أن‬ ‫اثبت‬ ‫>جـ‬ ‫ينصف‬ ‫ص‬ ‫جـ‬
1-‫دائرى‬ ‫رباعي‬ ‫ص‬ ‫س‬ ‫جـ‬ ‫ب‬
2-‫س‬ ‫ص‬ ‫جـ‬ ‫ب‬ // ‫ص‬ ‫س‬
‫جـ‬ ‫ب‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬31‫جـ‬ ‫ب‬ ‫منتصف‬ ‫د‬ ، ‫أجـ‬ = ‫أب‬ ‫فيه‬ ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ‫جـ‬ ‫ب‬ ‫أ‬ :
‫واحدة‬ ‫دائرة‬ ‫تمربها‬ ‫،هـ‬ ‫د‬ ، ‫ب‬ ، ‫أ‬ ‫أن‬ ‫اثبت‬ ‫جـ‬ ‫أ‬ ┴ ‫هـ‬ ‫ب‬
24

25. ‫س‬32=( ‫:ق)>جـ‬ ‫د‬ ‫جـ‬ = ‫ب‬ ‫جـ‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :140‫أ‬
(‫ق)>د‬ ، (‫ق)>أ‬ ‫أوجد‬
‫د‬ ‫م‬
‫جـ‬
‫ب‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬33= ( ‫ب‬ ‫أ‬ ) ‫ق‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :110=( ‫هـ‬ ‫ب‬ ‫جـ‬ >)‫ق‬ ،855
( ‫جـ‬ ‫د‬ ‫ق)>ب‬ ‫أوجد‬
‫د‬
‫جـ‬
85
‫أ‬ ‫ب‬ ‫هـ‬
110
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬34= (‫هـ‬ ‫ب‬ ‫أ‬ >)‫ق‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :1005
= ( ‫د‬ ‫أ‬ ‫جـ‬ >)‫ق‬ ،
405
(‫د‬ ‫أ‬ )‫ق‬ = (‫د‬ ‫جـ‬ )‫ق‬ ‫أن‬ ‫اثبت‬‫د‬ ‫أ‬
40
100
‫جـ‬ ‫ب‬ ‫هـ‬
25

26. ‫س‬35: ‫المقابل‬ ‫الشكل‬ ‫في‬ := (‫ق)>ب‬85‫ب‬ ‫أ‬
= ( ‫جـ‬ ‫أ‬ ‫د‬ >)‫ق‬35= ( ‫د‬ ‫جـ‬ ‫أ‬ )‫ق‬ ،5085
‫دائري‬ ‫رباعي‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫الشكل‬ ‫أن‬ ‫اثبت‬
35
50
‫جـ‬ ‫د‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬36‫د‬ ‫د‬ ‫أ‬ = ‫أب‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
= (‫د‬ ‫ب‬ ‫أ‬ >)‫ق‬305
=(‫هـ‬ ‫جـ‬ ‫د‬ >)‫ق‬120
‫دائري‬ ‫رباعي‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫الشكل‬ ‫أن‬ ‫اثبت‬
‫أ‬
30
‫هـ‬ ‫جـ‬ ‫ب‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬37= (‫ق)>أ‬ ‫مماسان‬ ‫جـ‬ ‫أ‬ ، ‫ب‬ ‫أ‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :455
1-‫دائري‬ ‫رباعي‬ ‫جـ‬ ‫م‬ ‫ب‬ ‫أ‬ ‫الشكل‬ ‫أن‬ ‫اثبت‬
2-‫ب‬ ‫د‬ ‫جـ‬ ‫م‬ ‫المثلث‬ ‫أن‬ ‫اثبت‬
‫م‬ ‫الساقين‬ ‫متساوي‬
‫د‬ ‫جـ‬ ‫أ‬
26

27. ‫س‬38= ( ‫جـ‬ >)‫ق‬ ‫مماسان‬ ‫ب‬ ‫س‬ ، ‫أ‬ ‫س‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬255
،
= (‫ق)>س‬705
‫ب‬ ‫س‬ // ‫أب‬ ، ( ‫س‬ ‫أ‬ ‫د‬ >) ‫ينصف‬ ‫ب‬ ‫أ‬ ‫أن‬ ‫اثبت‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬39= ( ‫ق)>م‬ ‫د‬ ‫جـ‬ // ‫ب‬ ‫أ‬ ، ‫مماسان‬ ‫جـ‬ ‫أ‬ ، ‫ب‬ ‫أ‬ :130
(‫ق)>أ‬ ‫وأوجد‬ ( ‫جـ‬ > ) ‫ينصف‬ ‫ب‬ ‫جـ‬ ‫أن‬ ‫اثبت‬
‫جـ‬
‫د‬
‫م‬ ‫أ‬130
‫ب‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬40‫مماسان‬ ‫د‬ ‫جـ‬ ، ‫ب‬ ‫أ‬ :
‫د‬ ‫جـ‬ = ‫أب‬ ‫أن‬ ‫اثبت‬
27

28. ‫س‬41(‫أ‬ >)‫ق‬ ‫أوجد‬ ، ‫مماسان‬ ‫جـ‬ ‫أ‬ ، ‫ب‬ ‫أ‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫ب‬
‫أ‬
65‫د‬
‫جـ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬42‫د‬ ‫ب‬ // ‫ص‬ ‫س‬ ، ‫مماس‬ ‫د‬ ‫ب‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬ :
‫دائري‬ ‫رباعي‬ ‫جـ‬ ‫ص‬ ‫س‬ ‫أ‬ ‫الشكل‬ ‫أن‬ ‫اثبت‬
‫أ‬
‫س‬
‫ب‬
‫جـ‬ ‫ص‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬43‫مماس‬ ‫د‬ ‫جـ‬ ‫أن‬ ‫اثبت‬ ‫جـ‬ ‫ب‬ = ‫جـ‬ ‫أ‬ ‫فيه‬ ‫أضل ع‬ ‫متوازي‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬ :
‫جـ‬ ‫ب‬ ‫أ‬ ‫للمثلث‬ ‫الخارجة‬ ‫للدائرة‬
28

29. 29