تتحدث الوثيقة عن تعريف الدالة في الرياضيات، حيث تُعرَّف بأنها علاقة تربط كل عنصر من مجموعة بأحد العناصر من مجموعة أخرى. تشمل الوثيقة أيضًا شرح كيفية تحديد المجال والمدى للدوال المختلفة، بما في ذلك الدوال كثيرة الحدود والدوال الكسرية، مع أمثلة تفصيلية توضح ذلك. تضمنت الوثيقة أيضًا كيفية تفسير الرسم البياني للدوال وكيفية التعامل مع المجالات والعناصر المرتبطة بها.
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١
اﻟﺪاﻟﺔ ﺗﻌﺮﯾﻒ:
ﻛﺎﻧﺖ إذاﺳﺲ،ﺻﺺﻣﻦ اﻟﻌﻼﻗﺔ ﻓﺈن ﺧﺎﻟﯿﺘﯿﻦ ﻏﯿﺮ ﻣﺠﻤﻮﻋﺘﯿﻦﺳﺲاﻟﻰﺻﺺداﻟﺔ ﺗﺴﻤﻰ
ﻋﻨﺎﺻﺮ ﻣﻦ ﻋﻨﺼﺮ ﻛﻞ ارﺗﺒﻂ إذاﺳﺲﻋﻨﺎﺻﺮ ﻣﻦ ﻓﻘﻂ واﺣﺪ ﺑﻌﻨﺼﺮﺻﺺ
د ﺗﻜﺘﺐ و:ﺳﺲCﺻﺺص أو=د)س(
ﺑﻄﺮﯾﻘﺘﯿﻦ اﻟﺪاﻟﺔ ﻋﻦ ﻧﻌﺒﺮ:
)١(اﻟﻤﺮﺗ اﻻزواج ﻣﻦ ﻛﻤﺠﻤﻮﻋﺔﺒﺔ)اﻟﺪاﻟﺔ ﺑﯿﺎن(د:ﺳﺲCﺻﺺ
)٢(اﻟﺪاﻟﺔ ﻗﺎﻋﺪة ﺗﺴﻤﻰ رﯾﺎﺿﯿﺔ ﺑﻘﺎﻋﺪة)اﻟﺪاﻟﺔ ﺗﺄﺧﺬھﺎ اﻟﺘﻰ اﻟﺼﻮر: (ص=د)س(
اﻟﻤﺪى و اﻟﻤﻘﺎﺑﻞ اﻟﻤﺠﺎل و اﻟﻤﺠﺎل:
ﻣﺎ ﻟﺪاﻟﺔ اﻟﻤﻘﺎﺑﻞ اﻟﺸﻜﻞ ﻣﻦ:
اﻟﻤﺠﺎل:
ھﻮاﻟﻌﻨ ﻣﺠﻤﻮﻋﺔﺎﺻاﻟﻤﺘﻐ ﯾﺄﺧﺬھﺎ اﻟﺘﻰ ﺮـاﻟﻨ ﯾﻜـﻮن ﺑﺤﯿﺚ س ﯿﺮﺎﺗﺞ
ﻣﻌﺮﻓﺔ ﻛﻤﯿﺔ"ﺣﻘﯿﻘﻰ ﻋـﺪد. "ﺳﺲ=}١،٢،٣،٤{
اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﻋﻠﻰ ﻗﯿﻤﮫ ﺗﻜﻮن و)اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﻋﻠﻰ اﻟﺒﯿﺎﻧﻰ ﻟﻠﺸﻜﻞ اﻟﻤﻘﺎﺑﻠﺔ اﻟﻔﺘﺮة(
اﻟﻤﻘﺎﺑﻞ اﻟﻤﺠﺎل:ﺗﺄﺧﺬھﺎ اﻟﺘﻰ اﻷﻋﺪاد ﻣﺠﻤﻮﻋﺔ ھﻮﺻﺺ=}٥،٦،٧،٨،٩{
اﻟﻤﺪى:}٦،٨،٩{
ﻋﻨﺎ ﺻﻮر ﻣﺠﻤﻮﻋﺔﺻﺮﺳﺲﻓﻰﺻﺺ
)س ﺑﻌﻨﺎﺻﺮ اﻟﻤﺮﺗﺒﻄﺔ ص ﻓﻰ اﻟﻌﻨﺎﺻﺮ(
ص اﻟﻤﺘﻐﯿﺮ ﯾﺄﺧﺬھﺎ اﻟﺘﻰ اﻟﺤﻘﯿﻘﯿﺔ اﻟﻌﻨﺎﺻﺮ ﻣﺠﻤﻮﻋﺔ ھﻮ
اﻟﺼﺎدات ﻣﺤﻮر ﻣﻦ ﺑﯿﺎﻧﯿﺎ ﻋﻠﯿﮫ وﻧﺤﺼﻞ
][ﻗﯿﻤﺔ أﺳﻔﻞ،ﻗﯿﻤﺔ أﻋﻠﻰ][
اﻟﺤﻘﯿﻘﯿﺔ اﻟﺪاﻟﺔ:ﻣﻦ ﺟﺰﺋﯿﺔ ﻣﺠﻤﻮﻋﺔ اﻟﻤﻘﺎﺑﻞ ﻣﺠﺎﻟﮭﺎ و ﻣﺠﺎﻟﮭﺎ ﻣﻦ ﻛﻞ داﻟﺔ ھﻰح
اﻷوﻟﻰ اﻟﻮﺣﺪة:اﻟﺤﻘﯿﻘﯿﺔ اﻟﺪوال](https://image.slidesharecdn.com/2017-160826233717/85/2017-1-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٢
اﻟﻌﺑﯿﺎﻧﯿﺎ داﻟﺔ ﺗﻜﻮن ﻼﻗﺔ)اﻟﺮأﺳﻰ اﻟﺨﻂ اﺧﺘﺒﺎر: (
اﻟﺮأﺳﻲ اﻟﺨﻂ ﻗﻄﻊ و ﻣﺘﻌﺎﻣﺪ اﺣﺪاﺛﻰ ﻣﺴﺘﻮى ﻓﻰ اﻟﻨﻘﺎط ﻣﻦ ﺑﻤﺠﻤﻮﻋﺔ ﻋﻼﻗﺔ ﻣﺜﻠﺚ إذا
داﻟﺔ ﺗﻤﺜﻞ اﻟﻌﻼﻗﺔ ھﺬه ﻓﺈن ﻓﻘﻂ ﻧﻘﻄﺔ ﻓﻰ اﻟﺒﯿﺎﻧﻰ ﺗﻤﺜﯿﻠﯿﮭﻤﺎ اﻟﻤﺠﺎل ﻋﻨﺎﺻﺮ ﻣﻦ ﻋﻨﺼﺮ ﻛﻞ ﻋﻨﺪ
ﻣﺜﺎل:د ﯾﻤﺜﻞ اﻵﺗﯿﺔ اﻻﺷﻜﺎل ﻣﻦ أﯾﺎ؟ ﻟﻤﺎذا و س ﻓﻰ اﻟﺔ
-٢
]١[
-١ ١ ٢ س
ص
٢
١
-١
-١ ١ ٢ س
ص
٢
١
-١
-١ ١ ٢ س
ص
٢
١
-١
-٢
-٢
-١ ١ ٢ س
ص
٢
١
-١
-٢
-٢
-١ ١ ٢ س
ص
٢
١
-١
-١ ١ ٢ س
ص
٢
١
-١
-٢-٢ ]٢[]٣[
]٦[ ]٥[ ]٤[](https://image.slidesharecdn.com/2017-160826233717/85/2017-2-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣
اﻟﺤﻞ:
اﻟﺸﻜﻞ]١: [
ﺑﺎﻟﻨﻘﻄﺔ اﻟﻤﺎر اﻟﺮأﺳﻰ اﻟﺨﻂ ﻷن داﻟﺔ ﯾﻤﺜﻞ ﻻ)٠،٠(ﻧﻘﻄﺘﯿﻦ ﻓﻰ اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ﯾﻘﻄﻊ
اﻟﺸﻜﻞ]٢: [
اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﻋﻠﻰ ﻧﻘﻄﺔ ﻛﻞ ﻋﻨﺪ اﻟﺮأﺳﻲ اﻟﺨﻂ ﻷن داﻟﺔ ﺗﻤﺜﻞ)اﻟﻤﺠﺎل(ﻓﻰ اﻟﻤﻨﺤﻨﻰ ﯾﻘﻄﻊ
واﺣ ﻧﻘﻄﺔﻓﻘﻂ ﺪة.
اﻟﺸﻜﻞ]٣: [ﻧﻘﻄﺔ ﻣﻦ أﻛﺜﺮ ﻓﻰ اﻟﻤﻨﺤﻨﻰ ﯾﻘﻄﻊ رأﺳﻲ ﺧﻂ ﯾﻮﺟﺪ ﻷن داﻟﺔ ﯾﻤﺜﻞ ﻻ.
اﻻﺷﻜﺎل]٤،٥،٦: [داﻟﺔ ﺗﻤﺜﻞ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻟﻤﺠﺎل ﻟﺘﻌﯿﯿﻦ ھـــﺎﻣﺔ ﻗـﻮاﻋــــﺪ:
١(أى ﻣﺠﺎلاﻟﺤﺪود ﻛﺜﯿﺮة داﻟﺔدرﺟﺘﮭﺎ ﻛﺎن ﻣﮭﻤﺎ=ح.
ﻣﺜﻞ اﻟﻤﻘﺎم ﻓﻰ ﻣﺘﻐﯿﺮ ﻋﻠﻰ ﺗﺤﺘﻮى ﻻ اﻟﺘﻰ اﻟﺪاﻟﺔ ھﻰ اﻟﺤﺪود ﻛﺜﯿﺮة اﻟﺪاﻟﺔ:
د)س= (٥د ،)س= (٣د ، س)س= (٢ــ س٥د ،)س= (س٢
+س+١
د)س= (س٣
ــ٢س+٤د ،)س= (
٢(ﻣﺠﺎلاﻟﻜﺴﺮﯾﺔ اﻟﺪاﻟﺔ=ح-اﻟﻤﻘــــــــﺎم أﺻﻔـــــــﺎر.
ﻣﺘﻐﯿﺮ ﻋﻠﻰ ﯾﺤﺘﻮى ﻣﻘﺎﻣﮭﺎ ﯾﻜﻮن اﻟﺘﻰ اﻟﺪاﻟﺔ ھﻰ اﻟﻜﺴﺮﯾﺔ اﻟﺪاﻟﺔ
ﻣﻠﺤﻮظﺔ:اﻟﻤﻘﺎم ﺗﺠﻌﻞ اﻟﺘﻰ س ﻗﯿﻢ ﻣﺠﻤﻮﻋﺔ ھﻰ اﻟﻤﻘﺎم أﺻﻔﺎر ﻣﺠﻤﻮﻋﺔ=ﺻﻔﺮ
د اﻟﺪاﻟﺔ ﻣﺠﺎل ﻟﻤﻌﺮﻓﺔ ﻣﺜﻼ)س= (اﻟﻤﻘﺎم أﺻﻔﺎر ﻧﻮﺟﺪ
س ﺑﻮﺿﻊ٢
ــ٩=٠Bس٢
=٩Bس=±٣Bد ﻣﺠﺎل)س= (ــ ح}٣ــ ،٣{
ﺧـــــﺎﺻﺔ ﺣـــﺎﻟﺔ:اﻟﻜﺴﺮﯾﺔ اﻟﺪاﻟﺔ ﻣﺠﺎل=اﻷﺗﯿﺔ اﻟﺤﺎﻻت ﻓﻰ ح:
*ﺛﺎﺑﺘﺔ داﻟﺔ اﻟﻤﻘﺎم.
*س اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻘﺎمن
+أن ﺣﯿﺚ←زوﺟﻰ،أЭح+
*س أ اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻘﺎم٢
+س ب+ﺟـ:ﺳﺎﻟﺒﺎ ﯾﻜﻮن اﻟﻤﻤﯿﺰ ﺣﯿﺚً.
ﻣﺜﻼ:د اﻟﺪاﻟﺔ ﻣﺠﺎل)س= (
س ﻧﻀﻊ٢
+٩=٠ﺣﯿﺚا=١،ب=٠،ج=٩
ــ س٣
٢
ــ س٢
س٢
ــ٩
ــ س٢
س٢
+٩](https://image.slidesharecdn.com/2017-160826233717/85/2017-3-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٤
اﻟﻤﻤﯿﺰ=ب٢
ــ٤ج ا=)٠(٢
ــ٤×١×٩=ــ٣٦>٠)ﺳﺎ ﻛﻤﯿﺔﻟﺒﺔ(
Bد ﻣﺠﺎل)س= (ح
٣(اﻟﺠﺬرﯾﺔ اﻟﺪاﻟﺔ ﻣﺠﺎل:
)اﻟﺘﺮﺑﯿﻌﻰ اﻟﺠﺬر ﻋﻠﻰ ﺗﺸﺘﻤﻞ اﻟﺪاﻟﺔ ﻗﺎﻋﺪة ﻛﺎﻧﺖ إذا ﺟﺬرﯾﺔ داﻟﺔ ﯾﻘﺎل(
أوﻻ:اﻟﺒﺴﻂ ﻓﻰ اﻟﺠﺬر ﻛﺎن إذا:اﻟﺠﺬر ﺗﺤﺖ ﻣﺎ اﻟﻔﺘﺮة ھﻮ اﻟﻤﺠﺎلX٠
ﺛﺎﻧﯿﺎ:اﻟﻤﻘﺎم ﻓﻰ اﻟﺠﺬر ﻛﺎن إذا:اﻟﺠﺬر ﺗﺤﺖ ﻣﺎ اﻟﻔﺘﺮة ھﻮ اﻟﻤﺠﺎل<٠
ﺧﺎﺻﺔ ﺣﺎﻟﺔ:
د اﻟﺪاﻟﺔ)س= (ن
؟ھـ)"س"("ﺣﯿﺚنgﺻﺺ+ھـ ،)س(ﺣﺪود ﻛﺜﯿﺮة
أوﻻ:ﻋﻨﺪﻣﺎنﻓﺈن ﻓﺮدى ﻋﺪد:اﻟﺪاﻟﺔ ﻣﺠﺎل=ح،ناﻟﺠﺬر دﻟﯿﻞ ﺗﺴﻤﻰ
ﺛﺎﻧﯿﺎ:ﻋﻨﺪﻣﺎنﻓﺈن زوﺟﻰ ﻋﺪد:ھـ ﺗﺠﻌﻞ اﻟﺘﻰ س ﻗﯿﻢ ﻣﺠﻤﻮﻋﺔ ھﻮ اﻟﺪاﻟﺔ ﻣﺠﺎل)س(X٠
أوﻻً:ﯾﻜ ﻋﻨﺪﻣﺎﻓــﺮدﯾﺎ اﻟﺠﺬر دﻟﯿﻞ ﻮنً:
ﻣﺜﻼد)س= (←د ﻣﺠﺎل)س= (ح
ﺛﺎﻧﯿﺎً:زوﺟﯿﺎ اﻟﺠﺬر دﻟﯿﻞ ﯾﻜﻮن ﻋﻨﺪﻣﺎ:
ﻣﺜﻼ:د)س= (
˙.˙ســ٥٠←س٥←د ﻣﺠﺎل)س] = (٥،]
ﻣﺜﺎل:ﻣﺠﺎل ﻋﯿﻦد)س= (
اﻟﺤﻞ:
ﺑﻮﺿﻊس٢
-س-١٢=٠
)س-٤)(س+٣= (٠
س-٤=٠س+٣=٠
س=٤س=-٣
٤-٣](https://image.slidesharecdn.com/2017-160826233717/85/2017-4-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥
˙.˙ﺳﺎﻟﺒﺔ ﻏﯿﺮ ﻛﻤﯿﺔ اﻟﺠﺬرﯾﺔ اﻟﺪاﻟﺔ ﻣﺠﺎل)٠(
.˙.د ﻣﺠﺎل)س] = (٤،]ﺑﻶ[-،-٣[
=ح-[ــ٣،٤]
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻵﺗﯿﺔ ﺑﺎﻟﻘﻮاﻋﺪ اﻟﻤﻌﺮﻓﺔ اﻟﺤﻘﯿﻘﯿﺔ اﻟﺪوال ﻣﻦ ﻛﻞ ﻣﺠﺎل ﻋﯿﻦ:
]١[د١)س= (؟س"+"٤"]٢[د٢)س= (؟س٢
"ــ"٩"
]٣[د٣)س] = (٤[د٤)س= (
]٥[د٥)س] = (٦[د٦)س= (٣
؟س"+"٣"
اﻟﺤﻞ:
]١[Aزوﺟﻰ اﻟﺠﺬر دﻟﯿﻞBس+٤X٠CسX–٤
Bاﻟﻤﺠﺎل=ح–]-٤،ﺿﺾ]
]٢[Aزوﺟﻰ اﻟﺠﺬر دﻟﯿﻞBس٢
–٩X٠Cس٢
X٩CسX±٣
Bاﻟﻤﺠﺎل[ =-ﺿﺾ،-٣[ﺑﻶ]٣،ﺿﺾ= ]ح-[–٣،٣]
]٣[س ﻧﻀﻊ٢
ــ٣س+٢=٠B)س–٢)(س–١= (٠Cس=٢،أ١
Bاﻟﻤﺠﺎل=ح–}١،٢{
]٤[س ﻧﻀﻊ٢
+٩=٠ﺳﺎﻟﺒﺔ ﻛﻤﯿﺔ اﻟﻤﻤﯿﺰ ﻓﯿﻜﻮنBاﻟﻤﺠﺎل=ح
]٥[س ﻧﻀﻊ٢
–٩<٠B)س–٣)(س+٣= (٠Cس=٣س ،=-٣
Aاﻟﺠﺬر ﺗﺤﺖ ﻣﺎ اﻟﻔﺘﺮة ھﻮ اﻟﻤﺠﺎل<٠Bاﻟﻤﺠﺎل=ح–]-٣،٣[
]٦[Aﻓﺮدى اﻟﺠﺬر دﻟﯿﻞBاﻟﻤﺠﺎل=ح
ــ س٢
س٢
+٩
٢س+٣
س٢
ــ٣س+٢
١
؟س٢
"ــ"٩"](https://image.slidesharecdn.com/2017-160826233717/85/2017-5-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٦
*ﻗﺎﻋﺪة ﻣﻦ ﺑﺄﻛﺜﺮ اﻟﻤﻌﺮﻓﺔ ﻟﻠﺪاﻟﺔ اﻟﻤﺪى و اﻟﻤﺠﺎل اﯾﺠﺎد:
ﻣﺜﺎل:ﻣﺪاھﺎ و ﻣﺠﺎﻟﮭﺎ اذﻛﺮ و اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ارﺳﻢ
)أ(د)س= ()ب(د)س= (
اﻟﺤﻞ:
)أ(س ﻋﻨﺪ>٠ﻣﻦ ﯾﺒﺪأ و اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﯾﻮازى ﺷﻌﺎع ﺗﻤﺜﻞ ﺛﺎﺑﺘﺔ داﻟﺔ)٠،-١(
س ﻋﻨﺪ<٠ﻣﻦ ﯾﺒﺪأ و اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﯾﻮازى ﺷﻌﺎع ﺗﻤﺜﻞ ﺛﺎﺑﺘﺔ داﻟﺔ)٠،١(
اﻟﻤﺠﺎل=ــ ح}٠{
اﻟﻤﺪى=}١،-١{
)ب(ﻗﺎﻋﺪة ﻟﻜﻞ ﺟﺪول ﻧﺮﺳﻢ
س>٠
سX٠
اﻟﻤﺠﺎل=اﻟﻤﺪى ، ح=ــ ح]-٢،٢]
س
٠-١-٢
د)س(-٢-٣-٤
س
٠١٢
د)س(٢٣٤
ــ١س>٠
١س<٠
س+٢سX٠
س–٢س>٠
٣
-٢ -١ ١ ٢ ٣
١
-١
٢
-٢ -١ ١ ٢ ٣ ٤
٣
٢
١
-١
-٢
-٣
](https://image.slidesharecdn.com/2017-160826233717/85/2017-6-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧
ﻣﺜﺎل:د ﻛﺎﻧﺖ إذا)س= (
اﻟﺒﯿ اﻟﺸﻜﻞ ارﺳﻢاﻟﺪاﻟﺔ ﻣﺪى و ﻣﺠﺎل اﺳﺘﻨﺘﺞ اﻟﺮﺳﻢ ﻣﻦ و ﻟﻠﺪاﻟﺔ ﺎﻧﻰ
اﻟﺤﻞ:
اﻟﺮﺳﻢ ﻣﻦ:اﻟﺪاﻟﺔ ﻣﺠﺎل] =-٢،∞]
اﻟﻤﺪى[ =-١،∞]
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:٣–ﻋﻨﺪﻣﺎ س-٢Yس>٢
د ﻛﺎﻧﺖ إذا)س= (
ﻋﻨﺪﻣﺎ س٢YسY٥
ا ارﺳﻢاﻟﺮﺳﻢ ﻣﻦ اﺳﺘﻨﺞ و ﻟﻠﺪاﻟﺔ اﻟﺒﯿﺎﻧﻰ ﻟﺸﻜﻞ
ﻣﺪاھﺎ و اﻟﺪاﻟﺔ ﻣﺠﺎل
اﻟﺤﻞ:
اﻟﻤﺠﺎل] =-٢،٥[اﻟﻤﺪى ،[ =١،٥[
س-٢-١٠٠١٢
د)س(٣٠-١١٢٣
س٢
-١-٢Yس>٠
س+١سX٠
س٢
–١س+١
-٢ -١ ١ ٢ ٣ ٤
٤
٣
٢
١
-١
-٢
](https://image.slidesharecdn.com/2017-160826233717/85/2017-7-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٨
ﻣﺜﺎل:د اﻟﺪاﻟﺔ ﻛﺎﻧﺖ إذا] :-٢،٤[Cﺣﯿﺚ ح
٢س+٣ﻋﻨﺪﻣﺎ-٢Yس>٠
د)س= (
١ﻋﻨﺪﻣﺎ س ــ٠YسY٤
اﻟﺪاﻟﺔ ﻣﺪى و ﻣﺠﺎل اﺳﺘﻨﺞ اﻟﺮﺳﻢ ﻣﻦ و د ﻟﻠﺪاﻟﺔ اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ارﺳﻢ
اﻟﺤﻞ:
-٢Yس>٠٠YسY٤
اﻟﻤﺠﺎل] =-٢،٤[
اﻟﻤﺪى] =-٣،٣]
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:إذاح ﺿﻠﻌﮫ طﻮل ﻓﻰ ﻛﺪاﻟﺔ اﻟﻤﺮﺑﻊ ﻣﺤﯿﻂ اﻛﺘﺐ ل ﺿﻠﻌﮫ طﻮل ﻣﺮﺑﻊ ﻣﺤﯿﻂ ح ﻛﺎن)ل(
أوﺟﺪ ﺛﻢ) :أ(ح)٣) (ب(ح( )
اﻟﺤﻞ:
Aح)ل= (٤×لBح)٣= (٤×٣=١٢ح ،= ( )٤×=١٥
س-٢-١٠٠١٤
ص-١١٣١٠-٣
٢-٢ -١ ١ ٣ ٤ -٣
٤
٣
٢
١
-١
-٢
-٣
-٤
١٥
٤
١٥
٤
١٥
٤](https://image.slidesharecdn.com/2017-160826233717/85/2017-8-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٩
اﻟـــ ﻋﻠﻰ اﻟﻌﻤﻠﯿﺎتـــــﺪوال
أن اﻟﺘﻌﺮﯾﻒ ھﺬا ﻣﻦ ﻧﻼﺣــﻆ:
ﺟﻤﯿﻊم ﯾﺴﺎوى اﻟﺠﺪﯾﺪة ﻟﻠﺪاﻟﺔ اﻟﻌﻤﻠﯿﺎت١ﺑﻼم٢اﻟﻤﻘﺎم داﻟﺔ ﺗﺠﻌﻞ اﻟﺘﻰ اﻟﻘﯿﻢ ﻋﺪا ﻣﺎ=ﻓﻰ ﺻﻔﺮ
اﻟﻘﺴﻤﺔ ﻋﻤﻠﯿﺔ.
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د ﺣﯿﺚ ﺣﻘﯿﻘﯿﺘﯿﻦ داﻟﺘﯿﻦ ر ، د ﻛﺎﻧﺖ إذا)س= (س٢
ــ٤ر ،)س= (؟ـ س"ـ١"
أوﺟﺪ) :أ(اﻵﺗﯿﺔ اﻟﺪوال ﻣﻦ ﻛﻞ ﻣﺠﺎل) :د+ر(،)د–ر(،)د.ر(،( )،( )
)ب(اﻟﻌﺪدﯾﺔ اﻟﻘﯿﻢ)أﻣﻜﻦ إن(اﻵﺗﯿﺔ اﻟﺪوال ﻣﻦ ﻟﻜﻞ:
)د+ر) (٥(،)د.ر) (٢(،)( )٣(،)( )-٢(
اﻟﺤﻞ:
Aد ﻣﺠﺎل=م١=ر ﻣﺠﺎل ، ح=م٢] =١،∞]د اﺻﻔﺎر ﻣﺠﻤﻮﻋﺔ ،=}٢،-٢{
ر اﺻﻔﺎر ﻣﺠﻤﻮﻋﺔ ،=}٠{
)أ) (د+ر) (س= (د)س+ (ر)س= (س٢
ــ٤+؟ـ س"ـ١"
Bﻣﺠﺎل)د+ر= (م١ﺑﻼم٢=حﺑﻼ]١،∞] = ]١،∞]
)ر ــ د)(س= (د)س(ر ــ)س= (س٢
ــ٤ــ؟ـ س"ـ١"
Bﻣﺠﺎل)ر ــ د= (م١ﺑﻼم٢=حﺑﻼ]١،∞] = ]١،∞]
( )
( )
( )
د
ر
ر
د
د
ر
ر
د
م١
ح
١
م٢
١](https://image.slidesharecdn.com/2017-160826233717/85/2017-9-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٠
)د.ر) (س= (د)س. (ر)س) = (س٢
ــ٤(؟ـ س"ـ١"
Bﻣﺠﺎل)د.ر= (م١ﺑﻼم٢=حﺑﻼ]١،∞] = ]١،∞]
) ( )س= = (
ﻣﺠﺎل) ( )س= (م١ﺑﻼم٢ص ــ)ر(
=حﺑﻼ]١،∞]ــ}١{[ =١،∞]
) ( )س= = (
ﻣﺠﺎل) ( )س= (م١ﺑﻼم٢ص ــ)د(
=حﺑﻼ]١،∞]ــ}٢،-٢{
=]١،∞]ــ}٢{س ﻋﻨﺪ ﻣﻌﺮﻓﺔ ﻏﯿﺮ اﻟﺪاﻟﺔ ﺣﯿﺚ=-٢
)ب()د+ر) (س= (س٢
ــ٤+؟ـ س"ـ١"س ﻟﻜﻞg]١،∞]
A٥g]١،∞]B)د+ر)(٥) = (٥(٢
ــ٤+؟٥–"١"=١٩
)د.ر) (س) = (س٢
ــ٤(؟ـ س"ـ١"س ﻟﻜﻞg]١،∞]
A٢g]١،∞]B)د.ر) (٢) = (٢٢
–٤(؟٢ـ"ـ١"=ﺻﻔﺮ
) ( )س= (س ﻟﻜﻞg[١،∞]
A٣g[١،∞]B)( )٣= = (
) ( )س= (س ﻟﻜﻞg]١،∞]ــ}٢{
A–٢h]١،∞]ــ}٢{B)( )-٢= = (ﻣﻌﺮﻓﺔ ﻏﯿﺮ
د
ر
د)س(
ر)س(
س٢
ــ٤
؟ـ س"ـ١" د
ر
م١
ح
١
م٢
١
ر
د
ر)س(
د)س(
؟ـ س"ـ١"
س٢
ــ٤
ر
د
حم١ ١
م٢
٢-٢
-٢ ٢
د
ر
س٢
ــ٤
؟ـ س"ـ١"
د
ر
٣٢
ــ٤
؟٣ـ"ـ١"
٥
؟٢
ر
د
؟ـ س"ـ١"
س٢
ــ٤
ر
د
؟-٢"ـ١"
)-٢(٢
–٤
؟-٣"
ﺻﻔﺮ](https://image.slidesharecdn.com/2017-160826233717/85/2017-10-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٢
ﺗﻌﺮﯾﻒ:
ر اﻟﺪاﻟﺔ ﻣﺠﺎل ﻣﻦ ﺟﺰﺋﯿﺔ ﻣﺠﻤﻮﻋﺔ د اﻟﺪاﻟﺔ ﻣﺪى وﻛﺎن داﻟﺘﯿﻦ د ،ر ﻛﺎﻧﺖ إذا
اﻟﺘﺮﻛﯿﺐ داﻟﺔ اﯾﺠﺎد ﯾﻤﻜﻦ ﻓﺈﻧﮫعاﻟﺠﺪ، د اﻟﺪاﻟﺘﯿﻦ ﻣﻦ ﺗﺘﺮﻛﺐ ﯾﺪةرھﻰ
ع)س) =(رºد) (س= (ر]د)س[ (
ﺗﻘﺮأ ورد ﺗﺮﻛﯿﺐأورد ﺑﻌﺪ
اﻟﺪاﻟﺔ ﺛﻢ أوﻻ د ﺗﻄﺒﻖ ﺣﯿﺚر
ﻣﻠﺤﻮظﺔ:اﻟﺪاﻟﺔ ﺗﻜﻮن أن ﻣﻤﻜﻦ)رºد) (س(
ﻣﻌﺮﻓﺔ ﻏﯿﺮ أو ﻣﻌﺮﻓﺔ]ﻣﻌﯿﻨﺔ ﻗﯿﻤﺔ ﻟﮭﺎأوﻗﯿﻤﺔ ﻟﮭﺎ ﻟﯿﺲ[
ﻋﻨﺪ اﻟﺪاﻟﺘﯿﻦ ﺗﺮﺗﯿﺐ ﻟﺬﻟﻚ وﻣﮭﻢ ﺗﺮﻛﯿﺒﮭﻤﺎ.
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د ﻛﺎن إذا)س= (٤س٢
ر ،)س= (٢أوﺟﺪ س) :دºر)(س(،)رºد)(س(
ﻣﺎ وﺗﻼﺣﻆ ذا.
اﻟﺤﻞ) :دºر)(س= (د]ر)س= [(د)٢س= (٤×)٢س(٢
=١٦س٢
)رºد)(س(=ر]د)س= [ (ر)٤س٢
= (٢×)٤س٢
= (٨س٢
أن ﯾﻼﺣﻆ) :دºر)(س(})رºد)(س()اﺑﺪاﻟﻰ ﻟﯿﺲ اﻟﺪوال ﺗﺮﻛﯿﺐ(
ﻣﻠﺤﻮظﺔ:ﻻﯾﺠﺎد)رºد)(س(ر اﻟﺪاﻟﺔ ﻓﻰ س اﻟﻤﺘﻐﯿﺮ ﻣﻦ ﺑﺪﻻ د ﺑﺎﻟﺪاﻟﺔ ﻧﻌﻮض
ر اﻟﺪاﻟﺔ ﺛﻢ أوﻻ د اﻟﺪاﻟﺔ ﻧﻮﺟﺪ.
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د ﻛﺎن إذا)س= (س٢
+٦ر ،)س= (٣س
أوﻻ:أوﺟﺪ)دºر) (٣(ﺛﺎﻧﯿﺎ:ﺗﺠﻌﻞ اﻟﺘﻰ س ﻗﯿﻢ ﺣﺪد)دºر) (س= (٤٢
د ﻣﺪى
ﻣﺠﺎلر
س د)س( ر]د)س[(
د ﻣﺠﺎل
ر]د)س[(
ر ﻣﺪى](https://image.slidesharecdn.com/2017-160826233717/85/2017-12-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٣
اﻟﺤﻞ:
أوﻻ) :دºر) (س= (د]ر)س= [ (د)٣س) = (٣س(٢
+٦=٩س٢
+٦
B)دºر) (٣= (٩)٣(٢
+٦=٨٧
آﺧﺮ ﺣﻞ:Aر)٣= (٣×٣=٩B)دºر) (٣= (د]ر)٣) = [ (٩(٢
+٦=٨٧
ﺛﺎﻧﯿﺎ:A)دºر) (س= (٤٢B٩س٢
+٦=٤٢B٩س٢
=٣٦ﺑﺎﻟﻘﺴﻤﺔ٩
Bس٢
=٤Bس=±٢
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د ﻛﺎن إذا)س= (س٢
+١ر ،)س= (؟ــ س"٣"
أوﺟﺪ) :دºر)(س(أوﺟﺪ ﺛﻢ اﻟﻤﺠﺎل ﻣﺤﺪدا ﺻﻮرة أﺑﺴﻂ ﻓﻰ)دºر) (٣(
اﻟﺤﻞ:
)دºر)(س= (د]ر)س= [ (د)؟ــ س"٣") = (؟ــ س"٣"(٢
+١
=س–٣+١=س–٢
ﻣﺠﺎل)دºر)(س= (}س:سX٣س ،gح{] =٣،∞]
)دºر) (٣= (٣–٢=١
آﺧﺮ ﺣﻞ) :دºر) (٣= (د]ر)٣= [(د)؟٣ــ"٣"= (د)٠) = (٠(٢
+١=١
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻟﻠﺘﻔﻜﯿﺮ ﺳﺆال:ع ﻛﺎن إذا)س= (؟س٣
""–"٤"ﯾ ﺑﺤﯿﺚ ر ، د اﻟﺪاﻟﺘﯿﻦ ﻓﺄوﺟﺪﻜﻮن
ع)س) = (دºر)(س(
اﻟﺤﻞ) :اﻟﺴﺆال ﻟﮭﺬا ﺣﻞ ﻣﻦ أﻛﺜﺮ ھﻨﺎك(
Aع)س= (؟س٣
""–"٤"=؟)س٣
"ــ"١("ــ"٣"
Bر)س(=س٣
ــ١د ،)س= (؟س"–"٣"ﺗﺤﻘﻖع)س) = (دºر)(س(
آﺧﺮ ﺣﻞ:Aع)س(=؟س٣
""–"٤"=؟)س٣
"ــ"٢("ــ"٢"
Bر)س(=س٣
ــ٢د ،)س= (؟س"–"١"ﺗﺤﻘﻖع)س) = (دºر)(س(
آﺧﺮ ﺣﻞ:Aع)س= (؟س٣
""–"٤"
Bر)س= (س٣
ــ٤د ،)س= (؟سﺗﺤﻘﻖع)س) = (دºر)(س(](https://image.slidesharecdn.com/2017-160826233717/85/2017-13-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٤
]١[داﻟﺔ ﺗﻤﺜﻞ ﻻ اﻵﺗﯿﺔ اﻟﻌﻼﻗﺎت ﻣﻦ اﯾﺎ:
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٢[اﻟﻌﻼﻗﺔ ﻋﺪا ﻣﺎ ﻓﻰ داﻟﺔ ص ﻓﯿﮭﺎ ﺗﻜﻮن اﻵﺗﯿﺔ اﻟﻌﻼﻗﺎت ﺟﻤﯿﻊ:
)١(ص=٢ــ س٣)٢(ص=س٢
ــ٤)٣(س=ص٢
–٢)٤(ص=س ﺣﺎ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٣[اﻻﺗﯿﺔ ﺑﺎﻟﻘﻮاﻋﺪ اﻟﻤﻌﺮﻓﺔ اﻟﺤﻘﯿﻘﯿﺔ اﻟﺪوال ﻣﻦ ﻛﻞ ﻣﺠﺎل ﻋﯿﻦ:
)١(د)س= (س٢
ــ٢س)٢(د)س= (ــ٥)٣(د)س= (؟٢س"ــ٣"
)٤(د)س) = (٥(د)س= (؟٤ــ""س٢
"")٦(د)س= (
ﺗﻤﺎرﯾﻦ)١(
س٢
-٩
س–٣
٣س+٢
؟س"+"٢"](https://image.slidesharecdn.com/2017-160826233717/85/2017-14-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٥
ــ٢س ﻋﻨﺪﻣﺎ>٢
٤س ﻋﻨﺪﻣﺎ س ـX٢
)٧(د)س) = (٨(د)س= (
)٩(د)س) = (١٠(د)س= (٣
؟س"
٢
+""س"-"٦"
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٤[ﻣﺪاھﺎ ﻋﯿﻦ و ﺑﯿﺎﻧﯿﺎ اﻻﺗﯿﺔ اﻟﺪوال ﻣﺜﻞ:
)١(د ﻛﺎﻧﺖ إذا] :-١،٥[Cد ، ح)س= (
د ﻣﻦ ﻛﻼ ﻓﺄوﺟﺪ)-١(د ،)٠(د ،)١(د ،)٢(د ،)٣(د ،)٤(د ،)٥(
ﻣﺪاھﺎ اﻟﺮﺳﻢ ﻣﻦ اﺳﺘﻨﺘﺞ و ﻟﻠﺪاﻟﺔ اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ارﺳﻢ ﺛﻢ.
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
)٢(د ﻛﺎﻧﺖ إذا)س= (
د ﻣﻦ ﻛﻼ ﻓﺎوﺟﺪ)٢(د ،)٣(د ،)٤(د ،)١(د ،)٠(د ،)-١(د ،)-٤(
ﻣﺪاھﺎ اﻟﺮﺳﻢ ﻣﻦ اﺳﺘﻨﺘﺞ و ﻟﻠﺪاﻟﺔ اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ارﺳﻢ ﺛﻢ.
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
)٣(د ﻛﺎﻧﺖ إذا] :-٣،٣[Cﺣﯿﺚ ح
د)س= (
اﻟﺪاﻟﺔ ھﺬه ﻣﺪى اﺳﺘﻨﺞ اﻟﺮﺳﻢ ﻣﻦ و ﻟﻠﺪاﻟﺔ اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ارﺳﻢ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
)٤(د ﻛﺎﻧﺖ إذا١:حCد ﺣﯿﺚ ح١)س= (٣س–١
د٢] :-٢،٣[Cد ﺣﯿﺚ ح٢)س= (٢س+٤
أوﺟﺪ) :د١+د٢) (س(،)د١د ــ٢) (س(ﻛ ﻣﺠﺎل ﻣﺒﯿﺎداﻟﺔ ﻞ.
ــ س٢
س٢
ــ٥س+٦
؟ــ س"٢"
س٢
ــ١
٤-ﻋﻨﺪﻣﺎ س-١Yس>٢
ﻋﻨﺪﻣﺎ س٢YسY٥
٢س ﻋﻨﺪﻣﺎ سX٢
س+٢س ﻋﻨﺪﻣﺎ>٢
س٢
+١ﻋﻨﺪﻣﺎ-٣Yس>٠
س+٢ﻋﻨﺪﻣﺎ٠YسY٣](https://image.slidesharecdn.com/2017-160826233717/85/2017-15-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٦
)٥(ﻛﺎن إذا:د١)س= (س+٢د ﻣﺠﺎل و١] =-٣،٤[د ،٢)س= (س٢
+٢س
د ﻣﺠﺎل و٢] =-١،٣[أوﺟﺪ:
)د١+د٢)(س(،)د١د ــ٢)(س(،)( )س(،)( )س(داﻟﺔ ﻛﻞ ﻣﺠﺎل ﻣﺒﯿﺎ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
)٦(ﻛﺎن إذا:د)س= (٣س+١ر ،)س= (س٢
–٥ق ،)س= (س٢
أوﺟﺪ:
)أ) (دºر) (٢) (ب) (رºد)(س()ﺟـ()رºق)(١()د()قºد)(-٢(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
)٧(ﻛﺎن إذا:د)س= (ر ،)س= (س+٣أوﺟﺪ:
)دºر)(س(،)رºد)(س(ﻣﻨﮭﻤﺎ ﻛﻞ ﻣﺠﺎل ﺣﺪد و.
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
)٨(د ﻛﺎن إذا)س= (س٢
–٣ر ،)س= (؟ــ س"٢"
أوﺟﺪ) :دºر)(س(أ ﻓﻰأوﺟﺪ ﺛﻢ اﻟﻤﺠﺎل ﻣﺤﺪدا ﺻﻮرة ﺑﺴﻂ)دºر) (٣(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
د١
د٢
د٢
د١
١
س](https://image.slidesharecdn.com/2017-160826233717/85/2017-16-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٧
]١[اﻟﺪوال ﻓﻰ اﻟﺘﻤﺎﺛﻞ:
ﺳﺒﻖ ﻟﻘﺪﻋﻠﻰ اﻟﺸﻜﻞ طﻰ ﯾﻤﻜﻦ ﺣﯿﺚ اﻷﺻﻞ ﻧﻘﻄﺔ و ﻣﺴﺘﻘﯿﻢ ﺣﻮل اﻟﺘﻤﺎﺛﻞ درﺳﻨﺎ أن
اﻟﻤﺴﺘﻘﯿﻢ)اﻷﺻﻞ ﻧﻘﻄﺔ أو(ﺗﻤﺎﻣﺎ اﻟﻤﻨﺤﻨﻰ ﻧﺼﻔﺎ ﻟﯿﻨﻄﺒﻖ.
)١(اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﺣﻮل اﻟﺘﻤﺎﺛﻞ:
اﻟﻤﻘﺎﺑﻞ اﻟﺸﻜﻞ ﻓﻰ:
اﻟﻨﻘﻄﺔ)، س-ص(اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ﻋﻠﻰ اﻟﻮاﻗﻌﺔ
اﻟﻨﻘﻄﺔ ﺻﻮرة ھﻰ اﻟﺪاﻟﺔ ﻟﻤﻨﺤﻨﻰ)، سص(
اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﺣﻮل ﺑﺎﻻﻧﻌﻜﺎس اﯾﻀﺎ ﻋﻠﯿﮫ اﻟﻮاﻗﻌﺔ
)٢(اﻟﺼﺎدات ﻣﺤﻮر ﺣﻮل اﻟﺘﻤﺎﺛﻞ:
اﻟﻤﻘﺎﺑﻞ اﻟﺸﻜﻞ ﻓﻰ:
اﻟﻨﻘﻄﺔ)-ص ، س(اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ﻋﻠﻰ اﻟﻮاﻗﻌﺔ
اﻟﻨﻘﻄﺔ ﺻﻮرة ھﻰ اﻟﺪاﻟﺔ ﻟﻤﻨﺤﻨﻰ)ص ، س(
اﻟﺼﺎدات ﻣﺤﻮر ﺣﻮل ﺑﺎﻻﻧﻌﻜﺎس أﯾﻀﺎ ﻋﻠﯿﮫ اﻟﻮاﻗﻌﺔ
ﻣﺜﻼ:اﻟﻨﻘﻄﺔ)-١،٠(اﻟﻨﻘﻄﺔ ﺻﻮرة)١،٠(
اﻟﺼﺎدات ﻣﺤﻮر ﺣﻮل ﺑﺎﻻﻧﻌﻜﺎس
اﻟﺪوال ﺧﻮاص ﺑﻌﺾ](https://image.slidesharecdn.com/2017-160826233717/85/2017-17-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٨
)٣(اﻷﺻﻞ ﻧﻘﻄﺔ ﺣﻮل اﻟﺘﻤﺎﺛﻞ:
اﻟﻤﻘﺎﺑﻞ اﻟﺸﻜﻞ ﻓﻰ:
اﻟﻨﻘﻄﺔ)-، س-ص(اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ﻋﻠﻰ اﻟﻮاﻗﻌﺔ
اﻟﻨﻘﻄﺔ ﺻﻮرة ھﻰ اﻟﺪاﻟﺔ ﻟﻤﻨﺤﻨﻰ)ص ، س(
ﺑﺎﻻﻧﻌﻜﺎس أﯾﻀﺎ اﻟﻤﻨﺤﻨﻰ ﻧﻔﺲ ﻋﻠﻰ اﻟﻮاﻗﻌﺔ
اﻷﺻﻞ ﻧﻘﻄﺔ ﺣﻮل
اﻟﻤﻘﺎﺑﻞ اﻟﺸﻜﻞ ﻓﻰ:
اﻷﺻﻞ ﻧﻘﻄﺔ ﺣﻮل ﻣﺘﻤﺎﺛﻞ اﻟﻤﻨﺤﻨﻰ
اﻟﻨﻘﻄﺔ ﻣﺜﻼ)١،١(اﻟﻨﻘﻄﺔ ﺻﻮرة)-١،-١(
اﻷﺻﻞ ﻧﻘﻄﺔ ﻓﻰ ﺑﺎﻻﻧﻌﻜﺎس
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٢[اﻟﻔﺮدﯾﺔ و اﻟﺰوﺟﯿﺔ اﻟﺪوال:]اﻟﺪوال ﻧﻮع[
أوﻻ:اﻟﺰوﺟﯿﺔ اﻟﺪاﻟﺔ:
ﺟﱪﻳﺎ:د اﻟﺪاﻟﺔ:س←صزوﺟﯿﺔ ﺗﻜﻮن
ﻛﺎﻧﺖ إذا:د)-س= (د)س(
س،-سgاﻟﻤﺠﺎل.]اﻟﺮﻣﺰﻟﻜﻞ ﯾﻘﺎل[
ﺑﻴﺎﻧﻴﺎ:اﻟﺼﺎدات ﺣﻮل ﻣﺘﻤﺎﺛﻼ ﻟﮭﺎ اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ﻛﺎن إذا زوﺟﯿﺔ اﻟﺪاﻟﺔ ﺗﻜﻮن.
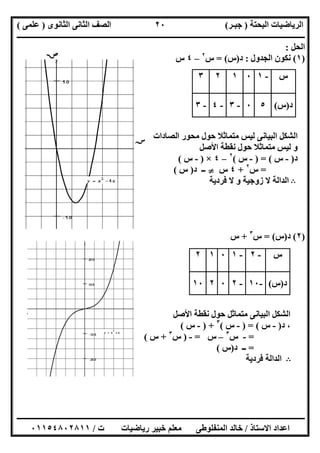
ﻛﺎﻧﺖ ﻓﺈذااﻟﻨﻘﻄﺔ)س،ص(gاﻟﻨﻘﻄﺔ ﻓﺈن اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ)-س،ص(gاﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ.](https://image.slidesharecdn.com/2017-160826233717/85/2017-18-320.jpg)

![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٢٢
]*٣[اﻷﺣﺎدﯾﺔ اﻟﺪاﻟﺔ:
ﻣﺜﺎل:أﺣﺎدﯾﺔ داﻟﺔ ر ، د اﻟﺪاﻟﺘﯿﻦ ﻣﻦ ﻛﻼ أن أﺛﺒﺖ:
)١(د)س= (س–٣)٢(ر)س= (
اﻟﺤﻞ) :١(ﻛﺎن إذاﺍب ،gد ، ح)ﺍ= (ﺍ–٣د ،)ب= (ب–٣
د ﺑﻮﺿﻊ)ﺍ= (د)ب(Bﺍ–٣=ب–٣ﺑﺤﺬف)-٣(اﻟﻄﺮﻓﯿﻦ ﻣﻦ
Bﺍ=ﺏBأﺣﺎدﯾﺔ داﻟﺔ د
)٢(ﻛﺎن إذاﺍب ،gح-}٥{،ر)ﺍ= (،ر)ﺏ= (
ﺑﻮﺿﻊر)ﺍ= (ر)ب(B=ﻧﺠﺪ اﻟﺘﺒﺎدﻟﻰ ﺑﺎﻟﻀﺮب
)٢ﺍ–٣) (ب–٥) = (ﺍ–٥()٢ب–٣(
٢ﺍب–٣ب–١٠ﺍ+١٥=٢ﺍب–١٠ب–٣ﺍ+١٥
١٠ب–٣ب=١٠ﺍ–٣ﺍ
B٧ب=٧ﺍBﺍ=بBرأﺣﺎدﯾﺔ داﻟﺔ
د اﻟﺪاﻟﺔ:ﺳﺲCﺻﺺأﺣﺎدﯾﺔ داﻟﺔ ﺗﺴﻤﻰ
ﻟﻜﻞ ﻛﺎن إذاﺍب ،gﺳﺲد ،)ﺍ= (د)ب(ﻓﺈنﺍ=ب
ﻟﻜﻞ أوﺍ}د ﻓﺈن ب)ﺍ(}د)ب(
اﻟﺪاﻟﺔ ﺑﯿﺎن ﻣﻦ واﺣﺪة ﻧﻘﻄﺔ ﻣﻦ ﺑﺄﻛﺜﺮ ﯾﻤﺮ ﻻ اﻟﺬى اﻷﻓﻘﻰ ﺑﺎﻟﺨﻂ ﺑﯿﺎﻧﯿﺎ ذﻟﻚ ﻣﻦ ﯾﺘﺤﻘﻖ و
٢س–٣
س–٥
٢ﺍ–٣
ﺍ–٥
٢ﺏ–٣
ﺏ–٥
٢ا–٣
ا–٥
٢ب–٣
ب–٥](https://image.slidesharecdn.com/2017-160826233717/85/2017-22-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٢٤
]٤[)اﻟــﺪاﻟـــــــﺔ اطـــــــــﺮاد(
ﺛﺎﺑﺘﺔ ﺗﻨﺎﻗﺼﯿﺔ ﺗﺰاﯾﺪﯾﺔ
١-)اﻟﺘﺰاﯾﺪﯾﺔ اﻟﺪاﻟﺔ(ﻟﻠﺪ ﯾﻘﺎلاﻟﻔﺘﺮة ﻓﻰ ﺗﺰاﯾﺪﯾﺔ أﻧﮭﺎ اﻟﺔ]ﺍ،ﺏ[
س ﻟﻜﻞ ﻛﺎن إذا١،س٢g]ﺍ،ﺏ[اﻵﺗﻰ اﻟﺸﺮط ﯾﺘﺤﻘﻖ:
س ﻛﺎن إذا١<س٢د)س١(<د)س٢(
ﻋﺎﻣــــﺔ وﺑﺼﻔﺔ:د)س(ﻛﺎﻧﺖ إذا ﺗﺰاﯾﺪﯾﺔ ﺗﻜﻮن:
ﺗﺘﺰاﯾﺪ اﻟﺪاﻟﺔ ﻗﯿﻤﺔس ﻗﯿﻤﺔ ﺑﺈزدﯾﺎد.
أﺧﺮى وﺑﻄﺮﯾﻘﺔ:د)س(ﻟﻤﻨﺤﻨﻰ اﻟﻤﻤﺎس ﻛﺎن إذا ﺗﺰاﯾﺪﯾﺔ ﺗﻜﻮن
اﻟﺴﯿﻨﺎت ﻟﻤﺤﻮر اﻟﻤﻮﺟﺐ اﻻﺗﺠﺎه ﻣﻊ ﺣﺎدة زاوﯾﺔ ﯾﺼﻨﻊ اﻟﺪاﻟﺔ.
٢-)اﻟﺘﻨﺎﻗﺼﯿﺔ اﻟﺪاﻟﺔ(اﻟﻔﺘﺮة ﻓﻰ ﺗﻨﺎﻗﺼﯿﺔ أﻧﮭﺎ ﻟﻠﺪاﻟﺔ ﯾﻘﺎل]ﺍ،ﺏ[
س ﻟﻜﻞ ﻛﺎن إذا١،س٢g]ﺍ،ﺏ[
اﻵﺗﻰ اﻟﺸﺮط ﯾﺘﺤﻘﻖ:
س ﻛﺎن إذا١<س٢د)س١(>د)س٢(
ﻋﺎﻣــــﺔ وﺑﺼﻔﺔ:د)س(ﻛﺎﻧﺖ إذا ﺗﻨﺎﻗﺼﯿﺔ ﺗﻜﻮن:س ﻗﯿﻤﺔ ﺑﺈزدﯾﺎد ﺗﺘﻨﺎﻗﺺ اﻟﺪاﻟﺔ ﻗﯿﻤﺔ.
أﺧﺮى وﺑﻄﺮﯾﻘﺔ:د)س(اﻟﻤﻤﺎس ﻛﺎن إذا ﺗﻨﺎﻗﺼﯿﺔ ﺗﻜﻮن
اﻟﺪاﻟﺔ ﻟﻤﻨﺤﻨﻰﻣﻨﻔ زاوﯾﺔ ﯾﺼﻨﻊاﻟﻤﻮﺟﺐ اﻻﺗﺠﺎه ﻣﻊ ﺮﺟﺔ
اﻟﺴﯿﻨﺎت ﻟﻤﺤﻮر.](https://image.slidesharecdn.com/2017-160826233717/85/2017-24-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٢٥
٣-)اﻟﺜﺎﺑﺘﮫ اﻟﺪاﻟﺔ(اﻟﻔﺘﺮة ﻓﻰ ﺛﺎﺑﺘﮫ أﻧﮭﺎ ﻟﻠﺪاﻟﺔ ﯾﻘﺎل]ﺍ،ﺏ[
س ﻟﻜﻞ ﻛﺎن إذا١،س٢g]ﺍ،ﺏ[
اﻵﺗﻰ اﻟﺸﺮط ﯾﺘﺤﻘﻖ:س ﻛﺎن إذا١<س٢د)س١= (د)س٢= (ﺍ
ﻋﺎﻣــــﺔ وﺑﺼﻔﺔ:د)س(س ﻗﯿﻤﺔ ﻛﺎﻧﺖ ﻣﮭﻤﺎ ﺛﺎﺑﺘﺔ اﻟﺪاﻟﺔ ﻗﯿﻤﺔ ﻛﺎﻧﺖ إذا ﺛﺎﺑﺘﺔ ﺗﻜﻮن.
اﻟﺨﻼﺻﺔ:
ﺗﺬﻛﺮأن:اﻟﺼﺎدات ﻣﺤﻮر ﻋﻠﻰ ﯾﻘﺮأ اﻟﻤﺪى أﻣﺎ اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﻋﻠﻰ ﺗﻘﺮأ اﻻطﺮاد ﻓﺘﺮات و اﻟﻤﺠﺎل
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻟﻤﺪى ذﻛﺮ ﻣﻊ اﻻﺗﯿﺔ اﻟﺪوال ﻣﻦ ﻛﻼ اطﺮاد اﺑﺤﺚ:
اﻟﺸﻜﻞ)١(اﻟﺸﻜﻞ)٢(اﻟﺸﻜﻞ)٣(
٥
٤
٣
٢
١
-١
-٢
-٢ -١ ٠ ١ ٢ ٣ ٤ ٥ -٢ -١ ٠ ١ ٢ ٣ ٤ ٥
٥
٤
٣
٢
١
-١
-٢
-٢ -١ ٠ ١ ٢ ٣ ٤ ٥
٥
٤
٣
٢
١
-١
-٢
](https://image.slidesharecdn.com/2017-160826233717/85/2017-25-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٢٦
اﻟﺤﻞ:
اﻟﺸﻜﻞ ﻓﻰ)١: (اﻟﻤﺪى] =٠،٢[
اﻻطﺮاد:ﻓﻰ ﻣﺘﺰاﯾﺪة اﻟﺪاﻟﺔ]-٢،٠[ﻓﻰ ﺛﺎﺑﺘﺔ ،]٠،٣[ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ ،]٣،٥[
اﻟﺸﻜﻞ ﻓﻰ)٢: (اﻟﻤﺪى] =-٢،∞]
اﻻطﺮاد:ﻓﻰ ﻣﺘﺰاﯾﺪة]١،∞]ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ ،[-∞،١[
اﻟﺸﻜﻞ ﻓﻰ)٣: (اﻟﻤﺪى[ =–∞،٣[
اﻻطﺮاد:اﻟﺪاﻟﺔﻓﻰ ﻣﺘﺰاﯾﺪة[-∞،٠[ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ ،]٣،∞]ﻓﻰ ﺛﺎﺑﺘﺔ ،]٠،٣[
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]١[ذﻟﻚ ﻏﯿﺮ أو ﻓﺮدﯾﺔ أو زوﺟﯿﺔ ﺣﯿﺚ ﻣﻦ اﻵﺗﯿﺔ اﻟﺪوال ﻧﻮع اﺑﺤﺚ) .ً ﺟﺒﺮﯾﺎ(
]١[د)س= (٢–س٢
]٢[د)س= (٤؟س]٣[د)س= (
]٤[د)س] = (٥[د)س= (س٣
+س ﺣﺘﺎ
]٦[د)س= (؟س٢
"+"٦"]٧[د)س=(
]٨[د)س= (س ﺣﺘﺎ س
اﻟﺪوال ﺧﻮاص ﺑﻌﺾ ﻋﻠﻰ ﺗﻤﺎرﯾﻦ
ــ س٣Cس<٠
ــ س ــ٣Cس>٠
س٣
ﺣﺎ٣س
١+س٤
ــ س١CسX٠
٧سCس>٠](https://image.slidesharecdn.com/2017-160826233717/85/2017-26-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٢٧
]٢[اﻟﺴ ذﻛﺮ ﻣﻊ ﯾﻠﻰ ﻛﻤﺎ اﻟﻤﻌﺮﻓﺔ اﻷﺣﺎدﯾﺔ اﻟﺪوال ﺣﺪد؟ ﺒﺐ
)١(د)س= (٣س+١)٢(د)س= (٢س٢
–س–٣
)٣(د)س= (س٤
+٢س+١)٤(د)س= (
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٣[ذﻟﻚ ﻏﯿﺮ أو ﻓﺮدﯾﺔ أو زوﺟﯿﺔ ﻛﻮﻧﮭﺎ ﺣﯿﺚ ﻣﻦ ﻧﻮﻋﮭﺎ وﺑﯿﻦ داﻟﺔ ﻛﻞ ﻣﺪى أوﺟﺪ:
٢س+١
س–١
٣
-٢ -١ ١ ٢ ٣
١
-١
٢
-٢ -١ ١ ٢ ٣ ٤
٣
٢
١
-١
-٢
-٣
-٢ -١ ١ ٢ ٣ ٤
٤
٣
٢
١
-١
-٢
]١[]٢[
]٣[ ]٤[](https://image.slidesharecdn.com/2017-160826233717/85/2017-27-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٢٨
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٤[ﻏﯿﺮ أﯾﮭﺎ و ﻓﺮدﯾﺔ ﻣﻨﮭﺎ أى و زوﺟﯿﺔ ﻣﻨﮭﺎ أى ﺑﯿﻦ ﺛﻢ ﯾﻠﻰ ﻛﻤﺎ اﻟﻤﻌﺮﻓﺔ اﻟﺪوال ﻣﻦ ﻛﻞ ارﺳﻢ
ﺟﺒﺮﯾﺎ ذﻟﻚ ﻣﻦ ﺗﺤﻘﻖ و ذﻟﻚ.
)أ(د)س= ()ب(د)س(=
)ﺟـ(د)س= ()د(د)س= (
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٥[
]٦[
]٦[ ]٥[
٢س ﻋﻨﺪﻣﺎ<٠
-٢ﻋﻨﺪﻣﺎس>٠
-س ﻋﻨﺪﻣﺎ سX٠
سﻋﻨﺪﻣﺎس>٠
س–١س ﻋﻨﺪﻣﺎX٠
٧سﻋﻨﺪﻣﺎس>٠
ﻗﺎاﻟﺠﯿﺐ ﻧﻮن)ﻗﺎﻋﺪة
اﻟﺠﯿﺐ(
س+١س ﻋﻨﺪﻣﺎX٠](https://image.slidesharecdn.com/2017-160826233717/85/2017-28-320.jpg)


![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣١
ﻣﺠﺎﻟﮭﺎ=ﻣﺪاھﺎ ، ح=ح
اطﺮادھﺎ:
ﻋﻨﺪﻣﺎ ﺗﺰاﯾﺪﯾﺔ اﻟﺪاﻟﺔا<٠)ﻣﻮﺟﺒﺔ(
ﻣﺜﻼ:د اﻟﺪاﻟﺔ)س(=٣س–٢ﻣﺘﺰاﯾﺪة
ﻋﻨﺪﻣﺎ ﺗﻨﺎﻗﺼﯿﺔ اﻟﺪاﻟﺔا>٠)ﺳﺎﻟﺒﺔ(
ﻣﺜﻼ:د اﻟﺪاﻟﺔ)س= (٢–٣ﻣﺘﻨﺎﻗﺼﺔ س
ﻧﻮﻋﮭﺎ:
ب ﻋﻨﺪﻣﺎ ﻓﺮدﯾﺔ ﻟﻜﻨﮭﺎ و ﻋﺎﻣﺔ ﺑﺼﻔﺔ ﻓﺮدﯾﺔ ﻟﯿﺴﺖ و زوﺟﯿﺔ ﻟﯿﺴﺖ اﻟﺪاﻟﺔ=٠
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:
د اﻟﺪاﻟﺔ ارﺳﻢ)س= (
ﻧﻮﻋﮭﺎ و اطﺮادھﺎ و اﻟﺪاﻟﺔ ﻣﺪى اﺳﺘﻨﺘﺞ اﻟﺮﺳﻢ ﻣﻦ و.
اﻟﺤﻞ:
اﻟﻤﺠﺎل] =-٤،٤[اﻟﻤﺪى ،] =٠،٢[
ﻣﺘﺰاﯾﺪ اﻟﺪاﻟﺔﻓﻰ ة]-٤،-٢[ﻓﻰ ﺛﺎﺑﺘﺔ ،[–٢،٢[
ﻓﻰ ﺗﻨﺎﻗﺼﯿﺔ ،[٢،٤[
اﻟﺼﺎدات ﻣﺤﻮر ﺣﻮل ﻣﺘﻤﺎﺛﻠﺔ ﻻﻧﮭﺎ زوﺟﯿﺔ اﻟﺪاﻟﺔ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:
د ﻟﻠﺪاﻟﺔ اﻟﻤﻨﺤﻨﻰ ارﺳﻢ)س= (
ﻧﻮﻋﮭﺎ و اطﺮادھﺎ و اﻟﺪاﻟﺔ ﻣﺪى اﺳﺘﻨﺘﺞ اﻟﺮﺳﻢ ﻣﻦ و
)٠ب ،(
)،٠( -ب
ا
ﺳﺺ
ﺳﺲ
س+٤س ،g]-٤،-٢[
٢س ،g[–٢،٢[
٤–س ، سg]٠،٢[
-٤ -٣ -٢ -١ ١ ٢ ٣ ٤
٤
٣
٢
١
-١
-٢
-٣
س+٢س ،X٠
ــ س٢س ،>٠](https://image.slidesharecdn.com/2017-160826233717/85/2017-31-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣٢
اﻟﺤﻞ:
سX٠س>٠
س٠١س٠-١
ص٢٣ص-٢-٣
اﻟﺪاﻟﺔ ﻣﺠﺎل=ح
اﻟﺪاﻟﺔ ﻣﺪى[ =-∞،-٢]ﺑﻶ]٢،∞]
ــ ح أو]-٢،٢]
ﻣﺠﺎﻟﮭﺎ ﻋﻠﻰ ﺗﺰاﯾﺪﯾﺔ اﻟﺪاﻟﺔ
زوﺟﯿﺔ ﻟﯿﺴﺖ و ﻓﺮدﯾﺔ ﻟﯿﺴﺖ اﻟﺪاﻟﺔ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*)اﻟﻤﻘﯿﺎس ﻣﻔﮭﻮم(ﺳﺎﻟﺐ ﻏﯿﺮ ﺣﻘﯿﻘﻰ ﻋﺪد ھﻮ)٠(
*)اﻟﻌــﺪد اﻟﻤﻘﯿﺎس(اﻟﻌﺪد ھﺬا ﻟﻤﺮﺑﻊ اﻟﻤﻮﺟﺐ اﻟﺘﺮﺑﯿﻌﻰ اﻟﺠﺬر ھﻮ.|س|=؟س٢
"
ﻣﺜﻼ:|-٥|=؟٢٥،|٣|=؟٩=٣،|٠|=٠،| |=
*دا رﺳﻢاﻟﻤﻘﯿﺎس ﻟﺔ) :اﻟﻤﻘﯿﺎس داﻟﺔ ﺧﻮاص(
ھﻰ اﻟﻌﺎﻣﺔ اﻟﺼﻮرة:د)س= (ك|س-ا|+ب،ك=±١
اﻟﻨﻘﻄﺔ ﻣﻦ ﺑﺸﻌﺎﻋﯿﻦ ﺑﯿﺎﻧﯿﺎ ﺗﻤﺜﻞ)اب ،(اﻟﻤﻨﺤﻨﻰ رأس ﻧﻘﻄﺔ ھﻰ)اب ،(
ا=ب ، اﻟﺴﯿﻨﯿﺔ اﻻزاﺣﺔ=س ھﻮ اﻟﺘﻤﺎﺛﻞ ﻣﺤﻮر ﻣﻌﺎدﻟﺔ ، اﻟﺼﺎدﯾﺔ اﻻزاﺣﺔ=ا
-٣ -٢ -١ ١ ٢ ٣ ٤
٦
٥
٤
٣
٢
١
-١
-٢
-٣
ﺛﺎﻟﺜﺎ:اﻟﻤﻘـﯿﺎس داﻟــﺔ)اﻟﻤﻄﻠﻘﺔ اﻟﻘﯿﻤﺔ(
١
٢
١
٢](https://image.slidesharecdn.com/2017-160826233717/85/2017-32-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣٣
اﻟﺪاﻟﺔ ﻣﺪى] =، ب∞]اﻟﺪاﻟﺔ ﻣﺪى[ =-∞ب ،[
ﻓﻰ ﺗﺰاﯾﺪﯾﺔ اﻟﺪاﻟﺔ]ا،∞]ﻓﻰ ﺗﺰاﯾﺪﯾﺔ اﻟﺪاﻟﺔ[-∞،ا[
ﻓﻰ ﺗﻨﺎﻗﺼﯿﺔ اﻟﺪاﻟﺔ[-∞،ا[ﻓ ﺗﻨﺎﻗﺼﯿﺔ اﻟﺪاﻟﺔﻰ]ا،∞]
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:
اﻟﺤﻞ:
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:
)اب ،(
)اب ،(
ك>٠)ﺳﺎﻟﺒﺔ
(
ك<٠)ﻣﻮﺟﺒﺔ(
ﺗﻨﺎﻗﺼﯿﺔ
ﺗﺰاﯾﺪﯾﺔ
ﺗﺰاﯾﺪﯾﺔ
ﺗﻨﺎﻗﺼﯿﺔ
اﻟﺤﻞ:](https://image.slidesharecdn.com/2017-160826233717/85/2017-33-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣٤
آﺧﺮ ﺣﻞ:ﻣﻨﺤﻨﻰ ﻧﻔﺲ اﻟﺪاﻟﺔ ھﺬه ﻣﻨﺤﻨﻰ|س|اﻟﻤﻮﺟﺐ اﻻﺗﺠﺎة ﻓﻰ وﺣﺪات ﺛﻼث ﺑﺎزاﺣﺔ ﻟﻜﻦ و
اﻟﺴﯿﻨﺎت ﻟﻤﺤﻮر.اﻟﺴﯿﻨﯿﺔ اﻻزاﺣﺔ=٣اﻟﺼﺎدﯾﺔ اﻻزاﺣﺔ و ،=٠
ﺳﺒﻖ ﻛﻤﺎ اﻟﺤﻞ ﻧﻜﻤـــــﻞ ﺛﻢ.
ﻣﻠﺤﻮظﺔ:
اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﻋﻠﻰ اﻻزاﺣﺔ=اﻟﻤﻘﯿﺎس ﺻﻔﺮ
اﻟﺼﺎدات ﻋﻠﻰ اﻻزاﺣﺔ=اﻟﻤﻘﯿﺎس ﺧﺎرج اﻟﻌﺪد)اﻟﻤﻘﯿﺎس اﻟﻰ اﻟﻤﻀﺎف اﻟﻌﺪد(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (-|س|واﻟﻣدى اﻟﻣﺟﺎل ذﻛر ﻣﻊ
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ وﺑﯾن اطرادھﺎ اﺑﺣث:
اﻟﺤﻞ:
اﻟﻤﻨﺤﻨ رأسﻰ)٠،٠(
ح اﻟﻤﺠﺎل
اﻟﻤﺪى[ =-،٠[
ﻓﻰ ﻣﺘﺰاﯾﺪة د[-،٠]
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د]٠،]
اﻟﺻﺎدات ﻣﺣور ﺣول ﻣﺗﻣﺎﺛﻠﺔ ﻷﻧﮭﺎ زوﺟﯾﺔ د
اﻟرﺑﻊ ﻓﻰ اﻷﺻل ﻧﻘطﺔ ﺑداﯾﺗﮭﻣﺎ ﺷﻌﺎﻋﯾن ﺑﯾﺎﻧﯾﺎ ﺗﻣﺛل
اﻟﻣﺣورﯾن ﺑﯾن اﻟزاوﯾﺔ ﯾﻧﺻﻔﺎن و اﻟراﺑﻊ و اﻟﺛﺎﻟث
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻟﻤﻘﯿﺎس ﻟﺪاﻟﺔ اﻟﮭﻨﺪﺳﯿﺔ اﻟﺘﺤﻮﯾﻼت٠
*اﻟﺮأﺳﯿﺔ اﻻزاﺣﺔ)اﻟﺼﺎدات ﻣﺤﻮر اﺗﺠﺎه ﻓﻰ(:
ﻣﺜﺎل:د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ارﺳﻢ)س= (|س|+٣وا اﻟﻤﺠﺎل ذﻛﺮ ﻣﻊوﺑﯿﻦ اطﺮادھﺎ اﺑﺤﺚ ﻟﻤﺪى
ذﻟﻚ ﻏﯿﺮ أو ﻓﺮدﯾﺔ أو زوﺟﯿﺔ ﻛﻮﻧﮭﺎ ﺣﯿﺚ ﻣﻦ ﻧﻮﻋﮭﺎ:
)٠،٠(
س′
ص′
-٣ -٢ -١ ١ ٢ ٣ ٤
٢
١
-١
-٢
اﻟﺤﻞ:](https://image.slidesharecdn.com/2017-160826233717/85/2017-34-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣٥
آﺧﺮ ﺣﻞ:اﻟﺴﯿﻨﯿﺔ اﻻزاﺣﺔ=٠اﻟﺼﺎدﯾﺔ اﻻزاﺣﺔ ،=٣
Bاﻟﺸﻌﺎﻋﯿﻦ ﻣﺒﺪا)٠،٣(اﻟﺤﻞ ﺑﻨﻔﺲ اﻟﺤﻞ ﻧﻜﻤﻞ ﻟﻠﻤﻨﺤﻨﻰ اﻟﺮأس ﻧﻘﻄﺔ ﺗﺴﻤﻰ
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (|س|-٢واﻟﻣدى اﻟﻣﺟﺎل ذﻛر ﻣﻊﺛموﺑﯾن اطرادھﺎ اﺑﺣث
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ:
اﻟﺣل:
اﻟﺮأس ﻧﻘﻄﺔ)٠،-٢(
ح اﻟﻤﺠﺎل
اﻟﻤﺪى] =-٢،]
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د[-،٠]
ﻓﻰ ﻣﺘﺰاﯾﺪة د]٠،]
اﻟﺼﺎدات ﻣﺤﻮر ﺣﻮل ﻣﺘﻤﺎﺛﻠﺔ ﻷﻧﮭﺎ زوﺟﯿﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ارﺳﻢ)س= (٢ــ|س|اﻟﺪاﻟﺔ ﻣﺪى و ﻣﺠﺎل ذﻛﺮ ﻣﻊ.
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ وﺑﯾن اطرادھﺎ اﺑﺣث:
اﻟﺤﻞ:
ح اﻟﻤﺠﺎل
اﻟﻤﺪى[ =-،٢[
ﻓﻰ ﻣﺘﺰاﯾﺪة د[-،٠]
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د]٠،]
اﻟﺻﺎدات ﻣﺣور ﺣول ﻣﺗﻣﺎﺛﻠﺔ ﻷﻧﮭﺎ زوﺟﯾﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ارﺳﻢ)س= (-|س|-٢اﻟﻤﺠﺎل ذﻛﺮ ﻣﻊواﻟﻤﺪى
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ وﺑﯾن اطرادھﺎ اﺑﺣث:
اﻟﺤﻞ:
ح اﻟﻤﺠﺎل
اﻟﻤﺪى[ =-،-٢[
ﻓﻰ ﻣﺘﺰاﯾﺪة د[-،٠]
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د]٠،]
اﻟﺼﺎدات ﻣﺤﻮر ﺣﻮل ﻣﺘﻤﺎﺛﻠﺔ ﻷﻧﮭﺎ زوﺟﯿﺔ د
)٠،-٢(
سس′
ص′
ص
)٢،٠()-٢،٠(
)٢،٠(
ص′
سس′
ص
)٠،٢(
)-٢،٠(
)٠،-٢(
س′
ص′
ص
س](https://image.slidesharecdn.com/2017-160826233717/85/2017-35-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣٦
*اﻷﻓﻘﯿﺔ اﻻزاﺣﺔ)اﻟﺴﯿﻨﺎت ﻣﺤﻮر اﺗﺠﺎه ﻓﻰ:(
ﻣﺜﺎل:ارﺳمد اﻟداﻟﺔ ﻣﻧﺣﻧﻰ)س= (|س–٢|واﻟﻣدى اﻟﻣﺟﺎل ذﻛر ﻣﻊ
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ وﺑﯾن اطرادھﺎ اﺑﺣث:
)اﻟﺤﻞ(
اﻟﺴﯿﻨﯿﺔ اﻻزاﺣﺔ=٢اﻟﺼﺎدﯾﺔ ،=٠Bاﻟﻤﻨﺤﻨﻰ راس)٢،٠(
ح اﻟﻤﺠﺎل
اﻟﻤﺪى] =٠،]
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د[-،٢]
ﻣﺘﺰاﯾﺪ دﻓﻰ ة]٢،]
وﻻﻓﺮدﯾﺔ ﻻزوﺟﯿﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ارﺳﻢ)س= (|س+٢|واﻟﻤﺪى اﻟﻤﺠﺎل ذﻛﺮ ﻣﻊ
اذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ وﺑﯾن اطرادھﺎ ﺑﺣث:
)اﻟﺤﻞ(
اﻟﺴﯿﻨﯿﺔ اﻻزاﺣﺔ=-٢اﻟﺼﺎدﯾﺔ ،=٠اﻟﻤﻨﺤﻨﻰ راس ،)-٢،٠(
ح اﻟﻤﺠﺎل
اﻟﻤﺪى] =٠،]
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د[-،-٢]
ﻓﻰ ﻣﺘﺰاﯾﺪة د]-٢،]
وﻻﻓردﯾﺔ ﻻزوﺟﯾﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ارﺳﻢ)س= (ــ|س–٢|واﻟﻤﺪى اﻟﻤﺠﺎل ذﻛﺮ ﻣﻊ
ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ وﺑﯾن اطرادھﺎ اﺑﺣثذﻟك ﻏﯾر أو:
)اﻟﺤﻞ(
اﻟﻤﻨﺤﻨﻰ رأس ﻧﻘﻄﺔ)٢،٠(
ح اﻟﻤﺠﺎل،اﻟﻤﺪى[ =-،٠[
ﻓﻰ ﻣﺘﺰاﯾﺪة د[-،٢]،ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د]٢،]
وﻻﻓردﯾﺔ ﻻزوﺟﯾﺔ د
)٢،٠(
سس′
ص
ص′
)٠،٢(
)-٢،٠(
سس′
ص
ص′
)٠،٢(
)٠،-٢(
س′ س
ص
ص′
)٢،٠(](https://image.slidesharecdn.com/2017-160826233717/85/2017-36-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣٧
ﻣﺜﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (-|س+٢|واﻟﻣدى اﻟﻣﺟﺎل ذﻛر ﻣﻊ
ﻣن ﻧوﻋﮭﺎ وﺑﯾن اطرادھﺎ اﺑﺣثذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث:
)اﻟﺤﻞ(
اﻟﻤﻨﺤﻨﻰ راس ﻧﻘﻄﺔ)-٢،٠(
ح اﻟﻤﺠﺎل
اﻟﻤﺪى[ =-،٠[
ﻓﻰ ﻣﺘﺰاﯾﺪة د[-،-٢]
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د]-٢،]
وﻻﻓردﯾﺔ ﻻزوﺟﯾﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻟﺮأﺳﯿﺔ و اﻷﻓﻘﯿﺔ اﻻزاﺣﺔ)اﻻﺣﺪاﺛﯿﺎت ﻣﺤﻮرى اﺗﺠﺎھﻰ ﻓﻰ(:
ﻣﺜﺎل:د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ارﺳﻢ)س= (-|س+٢|+٣واﻟﻤﺪى اﻟﻤﺠﺎل ذﻛﺮ ﻣﻊ
أ زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ وﺑﯾن اطرادھﺎ اﺑﺣثذﻟك ﻏﯾر أو ﻓردﯾﺔ و:
)اﻟﺤﻞ(
اﻟﺴﯿﻨﯿﺔ اﻻزاﺣﺔ=-٢اﻟﺼﺎدﯾﺔ اﻻزاﺣﺔ ،=٣
ح اﻟﻤﺠﺎل
اﻟﻤﺪى[ =-،٣[
ﻓﻰ ﻣﺘﺰاﯾﺪة د[-،-٢]
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ د]-٢،]
وﻻﻓردﯾﺔ ﻻزوﺟﯾﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:
اﻟﺤﻞ:
)٠،-٢(
س′ س
ص
ص′
)-٢،٠(
)٠،١(
س′ س
ص
ص′
)-٢،٣(](https://image.slidesharecdn.com/2017-160826233717/85/2017-37-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٣٩
ﻛﺎﻧﺖ إذا:ھﻰ اﻟﻌﺎﻣﺔ اﻟﺼﻮرةد)س= (ا)ب ــ س(٢
+ج،ا}٠
ﻷﺳﻔﻞ أو ﻷﻋﻠﻰ ﻓﺮﻋﯿﻦ ذو ﺑﻤﻨﺤﻨﻰ ﺑﯿﺎﻧﯿﺎ ﺗﻤﺜﻞ
اﻟﻤﻨﺤﻨﻰ اﻟﺮأس ﻧﻘﻄﺔ ﺗﻜﻮن و) =ﺟـ ، ب(
س ھﻰ اﻟﺘﻤﺎﺛﻞ ﺧﻂ ﻣﻌﺎدﻟﺔ ،=ب
اﻟﺴﯿﻨﯿﺔ اﻻزاﺣﺔ)اﻟﺴﯿﻨﺎت ﻣﺤﻮر اﺗﺠﺎه ﻓﻰ اﻻﻧﺘﻘﺎل= (ب
اﻟﺼﺎدﯾﺔ اﻻزاﺣﺔ ،)اﻟﺼﺎدات ﻣﺤﻮر اﺗﺠﺎه ﻓﻰ اﻻﻧﺘﻘﺎل= (ﺟـ
ﻛﺎن إذا:ا<٠)ﻣﻮﺟﺒﺔ(ﻛﺎن إذا:ا>٠)ﺳﺎﻟﺒﺔ(
اﻟﺪاﻟﺔ ﻣﺪى] =، ﺟـ∞]اﻟﺪاﻟﺔ ﻣﺪى[ =-∞ﺟـ ،[
ﻓﻰ ﺗﺰاﯾﺪﯾﺔ اﻟﺪاﻟﺔ]، ب∞]ﻓﻰ ﺗﺰاﯾﺪﯾﺔ اﻟﺪاﻟﺔ[-∞ب ،[
ﻓﻰ ﺗﻨﺎﻗﺼﯿﺔ اﻟﺪاﻟﺔ[-∞ب ،[ﺗﻨﺎﻗﺼﯿﺔ اﻟﺪاﻟﺔﻓﻰ]، ب∞]
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻟﺘﺮﺑﯿﻌﯿﺔ اﻟﺪاﻟﺔ
)ﺟـ ، ب(
)ﺟـ ، ب(
ﺗﺰاﯾﺪﯾﺔﺗﻨﺎﻗﺼﯿﺔ
ﺗﻨﺎﻗﺼﯿﺔﺗﺰاﯾﺪﯾﺔ
ﺻﻐﺮى ﻗﯿﻤﺔ
=ج
ا<٠
ا>٠
ﻋﻈﻤﻰ ﻗﯿﻤﺔ
=ج](https://image.slidesharecdn.com/2017-160826233717/85/2017-39-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٤١
)٢(ع)س= (ــ)س+٣(٢
د ﻣﻨﺤﻨﻰ ھﻮ)س= (س٢
اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﻓﻰ ﺑﺎﻻﻧﻌﻜﺎس
اﻟﺴﯿﻨﺎت ﻟﻤﺤﻮر اﻟﺴﺎﻟﺐ اﻻﺗﺠﺎه ﻓﻰ وﺣﺪات ﺑﺜﻼث ازاﺣﺘﮫ ﺛﻢ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*ﻣﺤﻮر اﺗﺠﺎه ﻓﻰ اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ إزاﺣﺔﺻﺺ)رأﺳﯿﺔ إزاﺣﺔ: (
ﻣﺜﺎل:د ﺣﯿﺚ د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ اﺳﺘﺨﺪم)س(س٢
ﺣﯿﺚ ع ، ر اﻟﺪاﻟﺘﯿﻦ ﻣﻦ ﻛﻞ ﻟﺘﻤﺜﯿﻞ:
)١(ر)س= (س٢
+٢)٢(ع)س= (س ــ٢
ــ١
اﻟﻤﻨﺤﻨﻰ رأس ﻧﻘﻄﺔ ﻋﯿﻦ اﻟﺮﺳﻢ ﻣﻦ واﻟﺪاﻟﺔ ﻣﺪى أوﺟﺪ و.
اﻟﺤﻞ:
)١(ر)س= (س٢
+٢
د ﻣﻨﺤﻨﻰ ھﻮ)س= (س٢
ﻓﻰ وﺣﺪﺗﯿﻦ ﺑﺎزاﺣﺔ
اﻟﺼﺎدات ﻟﻤﺤﻮر اﻟﻤﻮﺟﺐ اﻻﺗﺠﺎه
ھﻰ اﻟﻤﻨﺤﻨﻰ رأس ﻧﻘﻄﺔ)٠،٢(
اﻟﻤﺪى ،] =٢،∞]
ﺳﺺ
ﺳﺲ
)-٣،٠(
)٠،٩(
)٠،٢(
ﺻﺺ
ﺻﺲ](https://image.slidesharecdn.com/2017-160826233717/85/2017-41-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٤٢
)٢(ع)س= (س ــ٢
ــ١
د ﻣﻨﺤﻨﻰ ھﻮ)س= (س٢
اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﻓﻰ ﺑﺎﻻﻧﻌﻜﺎس
اﻟﺼﺎدات ﻟﻤﺤﻮر اﻟﺴﺎﻟﺐ اﻻﺗﺠﺎه ﻓﻰ واﺣﺪة وﺣﺪة ازاﺣﺔ ﺛﻢ
ھﻰ اﻟﻤﻨﺤﻨﻰ رأس ﻧﻘﻄﺔ)٠،-١(
اﻟﻤﺪى ،[ =-∞،-١[
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻹﺣﺪاﺛﯿﺎت ﻣﺤﻮرى اﺗﺠﺎھﻰ ﻓﻰ اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ إزاﺣﺔ:
ﻣﺜﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (٢-)س-١(٢
و اﻟﻣدى و اﻟﻣﻧﺣﻧﻰ رأس أوﺟد
اﻟ وﻧوع اﻻطراداﻟﺗﻣﺎﺛل ﻣﺣور ﻣﻌﺎدﻟﺔ و داﻟﺔ.
اﻟﺤﻞ:
اﻟﺴﯿﻨﯿﺔ اﻻزاﺣﺔ=١اﻟﺼﺎدﯾﺔ اﻻزاﺣﺔ ،=٢
Bاﻟﻤﻨﺤﻨﻰ راس)١،٢(
اﻟﺼﺎدات ﻣﺤﻮر ﻣﻊ اﻟﺘﻘﺎطﻊ ﻧﻘﻄﺔ ﻧﻮﺟﺪ ﺑﺪﻗﺔ ﻟﻠﺮﺳﻢ
س ﺑﻮﺿﻊ ذﻟﻚ و=٠C)٠،١(
اﻟﺘﻤﺎﺛﻞ ﻣﺤﻮر ﻣﻦ اﻟﻤﺴﺎﻓﺔ ﻧﻔﺲ ﻋﻠﻰ و
اﻟﻨﻘﻄﺔ ﻧﺴﺘﻨﺘﺞ و)٢،١(
اﻟﻤﺠﺎل=ح
اﻟﻤﺪى[ =-∞،٢[
اﻻطﺮاد:ﻓﻰ ﻣﺘﺰاﯾﺪة[-∞،١[
ﻓﻰ ﻣﺘﻨﺎﻗﺼﺔ]١،∞]
اﻟﻨﻮع:ﻓﺮدﯾﺔ ﻻ و زوﺟﯿﺔ ﻻ
اﻻﺻﻞ ﻧﻘﻄﺔ أو اﻟﺼﺎدات ﻣﺤﻮر ﺣﻮل ﺗﻤﺎﺛﻠﮭﺎ ﻟﻌﺪم
س اﻟﺘﻤﺎﺛﻞ ﻣﺤﻮر ﻣﻌﺎدﻟﺔ=١
ﺻﺲ
)٠،-١(
ﺻﺺ](https://image.slidesharecdn.com/2017-160826233717/85/2017-42-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٤٣
ﻣﺛﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ رﺳمُ)س= (-س٢
أﺟرﯾ ﺛمُاﻟﻣﻧﺣﻧﻰ ﻓﺄﺧذ ازاﺣﺎت ﻋﻠﯾﮫ تاﻟﺻورة
اﻵﺗﯾﺔ:د)س= (-)س+١(٢
-٢ذﻛر ﻣﻊ اﻟداﻟﺔ ﻗﺎﻋدة واذﻛر اﻹزاﺣﺎت ھذه ﻋﯾن
اﻟﺗﻣﺎﺛل ﻣﺣور وﻣﻌﺎدﻟﺔ اﻟﻣدى.
)اﻟﺤﻞ(
اﻟﺳﺎﻟب اﻻﺗﺟﺎه ﻓﻰ واﺣدة وﺣدة ﻣﻘدارھﺎ إزاﺣﺔ
ﺑﺈزاﺣﺔ ﻣﺗﺑوﻋﺔ اﻟﺳﯾﻧﺎت ﻟﻣﺣوروﺣدﺗﯾن ﻣﻘدارھﺎ
اﻻﺗ ﻓﻰﺟﺎهاﻟﺻﺎدات ﻟﻣﺣور اﻟﺳﺎﻟب.
ھﻰ اﻟداﻟﺔ ﻗﺎﻋدة:د)س= (-)س+١(٢
-٢
اﻟداﻟﺔ ﻣدى[ =-،-٢[
ھﻰ اﻟﺗﻣﺎﺛل ﻣﺣور ﻣﻌﺎدﻟﺔ:س=-١
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺛﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س(=س٢
+٤س+٦واوﻣﻌﺎدﻟﺔ ﻣداھﺎ واذﻛر اطرادھﺎ ﺑﺣثﻣﺣور
د اﻟﻣﻧﺣﻧﻰ ﻣن اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ﻋﻠﻰ اﻟﺣﺻول ﯾﻣﻛن ﻛﯾف ﺑﯾن ﺛم ، اﻟﺗﻣﺎﺛل)س= (س٢
)اﻟﺤﻞ(
ﻟﻠداﻟﺔ اﻟﻘﯾﺎﺳﯾﺔ اﻟﺻورة اﻟﻰ اﻟداﻟﺔ ﺗﻌرﯾف اﻋﺎدة ﯾﺟب
د)س) = (س٢
+٤س+٤(+٦-٤) =س+٢(٢
+٢
ﻓﻰ ﻣﺗﻧﺎﻗﺻﺔ د ،[-،-٢]،ﻓﻰ ﻣﺗزاﯾدة د]-٢،]
وﻻﻓردﯾﺔ زوﺟﯾﺔ ﻟﯾﺳت د ،
اﻟﻣدى ،] =٢،]
س ھﻰ اﻟﺗﻣﺎﺛل ﻣﺣور ﻣﻌﺎدﻟﺔ ،=-٢
د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ﻋﻠﻰ اﻟﺣﺻول وﯾﺗم ،)س= (س٢
+٤س+٦
د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ﻣن)س= (س٢
وذﻟك
اﻟﺳ اﻻﺗﺟﺎه ﻓﻰ وﺣدﺗﯾن ﻣﻘدارھﺎ ﺑﺈزاﺣﺔﺎﻟب
وﺣدﺗﯾن ﻣﻘدارھﺎ ﺑﺈزاﺣﺔ ﻣﺗﺑوﻋﺔ ، اﻟﺳﯾﻧﺎت ﻟﻣﺣور
اﻟﺻﺎدات ﻟﻣﺣور اﻟﻣوﺟب اﻻﺗﺟﺎه ﻓﻰ
س
ص
)-١،-٢(
)٠،-٣(
س′
ص′
و
س
ص
)-٢،٢(
)٠،٦(
وس′
ص′](https://image.slidesharecdn.com/2017-160826233717/85/2017-43-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٤٧
اﻟﻌﺎﻣﺔ اﻟﺼﻮرة:د)س+ = (ك ، ﺟـ}٠س ،}ب
ھﻰ اﻟﺘﻤﺎﺛﻞ ﻧﻘﻄﺔ)ﺟـ ، ب(
ﻣﺠﺎﻟﮭﺎ وﯾﻜﻮن=ح–}ب{ﻣﺪاھﺎ ،=ح–}ﺟـ{
ﻣﻠﺤﻮظﺔ:اﻟﺘﻤﺎﺛﻞ ﻧﻘﻄﺔ ﻛﺎﻧﺖ إذا)٠،٠(ﻓﺮدﯾﺔ اﻟﺪاﻟﺔ ﻓﺄن
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺛﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (ﻧوﻋﮭﺎ واذﻛر اطرادھﺎ واﺑﺣث واﻟﻣدى اﻟﻣﺟﺎل واذﻛر
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن:
اﻟﺣل:
اﻟﻣﺟﺎل=ح–}٠{
اﻟﻣدى=ح–}٠{
ﻓﻰ ﻣﺗﻧﺎﻗﺻﺔ د[-،٠]،[٠،]
اﻷﺻل ﻧﻘطﺔ ﺣول ﻣﺗﻣﺎﺛﻠﺔ ﻷﻧﮭﺎ ﻓردﯾﺔ د
ك
س-ب
)-ﺟـ ، ب(
س
ص
س′
ص′
سس′
ص
ص′
)، بﺟـ(
ﻓﻰ ﺗﻨﺎﻗﺼﯿﺔ اﻟﺪاﻟﺔ[، ب∞]،[-∞ب ،]
اﻟﺜﺎﻟﺚ و اﻻول اﻟﺮﺑﻌﯿﻦ ﻓﻰ ﯾﻘﻊ اﻟﻤﻨﺤﻨﻰ
ﻓﺮدﯾﺔ وﻻ زوﺟﯿﺔ ﻻ اﻟﺪاﻟﺔ
ﻓﻰ ﺗﺰاﯾﺪﯾﺔ اﻟﺪاﻟﺔ[-∞،-ب]،[-،ب∞]
اﻟاﻟﺮاﺑﻊ و اﻟﺜﺎﻧﻰ اﻟﺮﺑﻌﯿﻦ ﻓﻰ ﯾﻘﻊ ﻤﻨﺤﻨﻰ
ﻓﺮدﯾﺔ وﻻ زوﺟﯿﺔ ﻻ اﻟﺪاﻟﺔ
اﻟﺪاﻟﺔاﻟﻜﺴﺮﯾﺔ
)٠،٠(
س
ص
س′
ص′
١
س](https://image.slidesharecdn.com/2017-160826233717/85/2017-47-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٤٨
ﻣﺛﺎل:ﻣﻧﺣﻧﻰ ارﺳمد اﻟداﻟﺔ)س= (ﻧوﻋﮭﺎ واذﻛر اطرادھﺎ واﺑﺣث واﻟﻣدى اﻟﻣﺟﺎل واذﻛر
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن:
اﻟﺤﻞ:
اﻟﻣﺟﺎل=ح–}٠{
اﻟﻣدى=ح–}٠{
ﻓﻰ ﻣﺗزاﯾدة د[-،٠]،[٠،]
اﻷﺻل ﻧﻘطﺔ ﺣول ﻣﺗﻣﺎﺛﻠﺔ ﻷﻧﮭﺎ ﻓردﯾﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻟﻜﺴﺮﯾﺔ ﻟﻠﺪاﻟﺔ اﻟﮭﻨﺪﺳﯿﺔ اﻟﺘﺤﻮﯾﻼت) :اﻻﺣﺪاﺛﯿﺎت ﻣﺤﻮرى اﺗﺠﺎھﻰ ﻓﻰ(
ﻣﺛﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (و واﻟﻣدى اﻟﻣﺟﺎل واذﻛراطرادھﺎ اﺑﺣث
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ واذﻛر:
اﻟﺤﻞ:
اﻟﻣﺟﺎل=ح–}٢{
اﻟﻣدى=ح–}٠{
ﻓﻰ ﻣﺗزاﯾدة د[-،٢]،[٢،]
وﻻزوﺟﯾﺔ ﻻﻓردﯾﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺛﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (-+٢اطرادھﺎ واﺑﺣث واﻟﻣدى اﻟﻣﺟﺎل واذﻛر
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ واذﻛر:
اﻟﺣل:
اﻟﻣﺟﺎل=ح–}-١{
اﻟﻣدى=ح–}٢{
ﻓﻰ ﻣﺗزاﯾدة د[-،-١]،[-١،]
وﻻزوﺟﯾﺔ ﻻﻓردﯾﺔ د
-١
س
)٠،٠(
س
ص
س′
ص′
-١
س-٢
)٢،٠(
س
ص
س′
ص′
١
س+١
)-١،٢(
س
ص
س′
ص′](https://image.slidesharecdn.com/2017-160826233717/85/2017-48-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٤٩
ﻣﺛﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (اطرادھﺎ واﺑﺣث واﻟﻣدى اﻟﻣﺟﺎل واذﻛر
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ واذﻛر:
اﻟﺤﻞ:
د)س= (-=٢-
اﻟﻣﺟﺎل=ح–}٠{
اﻟﻣدى=ح–}٢{
ﻓﻰ ﻣﺗزاﯾدة د[-،٠]،[٠،]
وﻻزوﺟﯾﺔ ﻻﻓردﯾﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺛﺎل:ارﺳمد اﻟداﻟﺔ ﻣﻧﺣﻧﻰ)س= (اطرادھﺎ واﺑﺣث واﻟﻣدى اﻟﻣﺟﺎل واذﻛر
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ واذﻛر:
اﻟﺤﻞ:
د)س= = = (٣+
اﻟﻣﺟﺎل=ح–}١{
اﻟﻣدى=ح–}٣{
دﻓﻰ ﻣﺗﻧﺎﻗﺻﺔ[-،١]،[١،]
وﻻزوﺟﯾﺔ ﻻﻓردﯾﺔ د
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د اﻟداﻟﺔ ﻣﻧﺣﻧﻰ ارﺳم)س= (واذﻛراطرادھﺎ واﺑﺣث واﻟﻣدى اﻟﻣﺟﺎل
ذﻟك ﻏﯾر أو ﻓردﯾﺔ أو زوﺟﯾﺔ ﻛوﻧﮭﺎ ﺣﯾث ﻣن ﻧوﻋﮭﺎ واذﻛر:
اﻟﺤﻞ:
د)س= = = (٢–
٢س-١
س
٢س
س
١
س
١
س
ص
)٠،٢(
سس′
ص′
٣س-٢
س-١
٣س–٣–٢+٣
س-١
٣)س–١+ (١
)س–١(
١
س-١
سس′
ص
ص′
)١،٣(
٢س-١
س+١
٢س+٢–١-٢
س+١
٢)س+١(–٣
س+١
٣
س+١](https://image.slidesharecdn.com/2017-160826233717/85/2017-49-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٠
اﻟﺘﻤﺎﺛﻞ ﻧﻘﻄﺔ)-١،٢(
اﻟﻤﺠﺎل=ح–}-١{
اﻟﻤﺪى=ح–}٢{
ﻣﺘﺰ اﻟﺪاﻟﺔﻓﻰ اﯾﺪة[-∞،-١]،[–١،∞]
زوﺟﯿﺔ ﻻ و ﻓﺮدﯾﺔ ﻻ اﻟﺪاﻟﺔ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د ﺣﯿﺚ د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ اﺳﺘﺨﺪم)س= (س ﺣﯿﺚ}٠ﻟﺘﻤﺜﯿﻞ:
)أ(د)س) = (ب(د)س+ = (٣
اﻟﺤﻞ:
)أ) (ب(
)-١،٢(
س
ص
س′
ص′
١
س-١
١
س
١
س+٣](https://image.slidesharecdn.com/2017-160826233717/85/2017-50-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥١
ﺑﺎﻟﻘﻮ اﻟﻤﻌﺮﻓﺔ اﻟﺪوال ﻣﻦ ﻛﻼ ﺑﯿﺎﻧﯿﺎ ﻣﺜﻞﻛﻞ ﻣﺪى و ﻣﺠﺎل أوﺟﺪ اﻟﺮﺳﻢ ﻣﻦ و اﻻﺗﯿﺔ اﻋﺪ
ذﻟﻚ ﻏﯿﺮ أو ﻓﺮدﯾﺔ أو زوﺟﯿﺔ ﻛﻮﻧﮭﺎ ﺣﯿﺚ ﻣﻦ ﻧﻮﻋﮭﺎ و اطﺮادھﺎ اﺑﺤﺚ و داﻟﺔ.
]١[د)س= (س]٢[د)س= (٢س+٣
]٣[د)س] = (٤[د)س= (
]٥[د)س] = (٦[د)س= (
]٧[د)س] = (٨[د)س= (
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
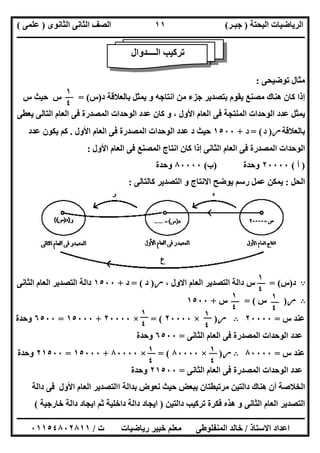
ﻣﺜﺎل:اﻟﻤﻌﻄﺎة اﻻﺟﺎﺑﺎت ﺑﯿﻦ ﻣﻦ اﻟﺼﺤﯿﺤﺔ اﻻﺟﺎﺑﺔ اﺧﺘﺮ:
)١(اﻟﻤﻘﺎﺑﻞ ﺑﺎﻟﺸﻜﻞ اﻟﻤﻤﺜﻠﺔ اﻟﺪاﻟﺔ ﻣﺪى:ھﻮ..........
)أ(}١{)ب(}١،-١{)ﺟـ(}-١{)د(ح
)٢(د اﻟﺪاﻟﺔ:د)س= (٣–ﺗﻜﻮن س.................
)أ(ح ﻋﻠﻰ ﺗﺰاﯾﺪﯾﺔ)ب(ح ﻋﻠﻰ ﺗﻨﺎﻗﺼﯿﺔ
)ﺟـ(ﻓﻰ ﺗﺰاﯾﺪﯾﺔ[٣،∞) ]د(ﻓﻰ ﺗﻨﺎﻗﺼﯿﺔ]٣،∞]
اﻟﻤﻨﺤﻨﯿﺎت رﺳﻢ ﻋﻠﻰ ﺗﻤﺎرﯾﻦ
اﻟﺨﻄﯿﺔ و اﻟﺜﺎﺑﺘﺔ اﻟﺪاﻟﺔ ﻋﻠﻰ ﺗﺪرﯾﺐ
٣س٢
ــ٣
س٢
–١
س٣
س ــ
س٢
–س
٢س ،Y٠
ــ٢س ،<٠
س ، سX٠
س ، س ــ>٠
٣س ، سg]٠،٢[
٦س ،g[٢،٤]
س+٢س ،g]٤،٦[
س+١س ،>١
٢،١>س>٣
س ، سX٠
و
١
-١
س
ص](https://image.slidesharecdn.com/2017-160826233717/85/2017-51-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٢
*ﺗﺪرﯾﺐاﻟﻤﻘﯿﺎس داﻟﺔ ﻋﻠﻰ:
]١[ﺑﺎﻟﻘﻮ اﻟﻤﻌﺮﻓﺔ اﻟﺪوال ﻣﻦ ﻛﻼ ﺑﯿﺎﻧﯿﺎ ﻣﺜﻞداﻟﺔ ﻛﻞ ﻣﺪى و ﻣﺠﺎل أوﺟﺪ اﻟﺮﺳﻢ ﻣﻦ و اﻻﺗﯿﺔ اﻋﺪ
ذﻟﻚ ﻏﯿﺮ أو ﻓﺮدﯾﺔ أو زوﺟﯿﺔ ﻛﻮﻧﮭﺎ ﺣﯿﺚ ﻣﻦ ﻧﻮﻋﮭﺎ و اطﺮادھﺎ اﺑﺤﺚ و.
وﺟﺪ إن اﻟﺘﻤﺎﺛﻞ ﻣﺤﻮر ﻣﻌﺎدﻟﺔ اذﻛﺮ و.
)١(د)س= (|س|+٤)٢(د)س= (|س–٣|
)٣(ر)س= (|س|+س)٤(ر)س= (|٢س+٣|+٣س–١
)٥(د)س= (|س+٣|)٦(د)س= (|س–٢|+٣
)٧(د)س= (١ــ|س–٢|)٨(د)س= (|٤س–٢س|ــ٣
)٩(د)س= (ــ س|ــ س٣|)١٠(د)س= (٢ــ|س|
]٢[د ﺣﯿﺚ د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ اﺳﺘﺨﺪم)س= (|س|ع ، ر اﻟﺪاﻟﺘﯿﻦ ﻣﻦ ﻛﻞ ﻟﺘﻤﺜﯿﻞ:
)أ(ر)س= (|س+٤|)ب(ع)س= (|س–٢|
)ﺣـ(ر)س= (|س|-٥)ء(ع)س= (|س|+٦
)ھـ(ر)س(=|س+٣|-١)و(ع)س= (|س–٢|+٤
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻟﺘﺮﺑﯿﻌﯿﺔ اﻟﺪاﻟﺔ ﻋﻠﻰ ﺗﺪرﯾﺐ:
]١[اﻟﺪ ﻣﻨﺤﻨﻰ اﺳﺘﺨﺪمد ﺣﯿﺚ د اﻟﺔ)س= (س٢
ﺣﯿﺚ ع ، ر اﻟﺪاﻟﺘﯿﻦ ﻣﻦ ﻛﻞ ﻟﺘﻤﺜﯿﻞ:
)أ(ر)س) = (س+٢(٢
ــ٤)ب(ع)س= (٢ــ)ــ س٣(٢
اﻟﻤﻨﺤﻨﻰ ﺗﻘﺎطﻊ ﻧﻘﻂ إﺣﺪاﺛﯿﺎت و اﻟﻤﻨﺤﻨﻰ رأس ﻧﻘﻄﺔ إﺣﺪاﺛﻰ ﻋﯿﻦ اﻟﺮﺳﻢ ﻣﻦ و
اﻟﺪاﻟ ﻣﻦ ﻛﻞ إطﺮاد اﺑﺤﺚ و ، اﻹﺣﺪاﺛﯿﺎت ﻣﺤﻮرى ﻣﻊﺘﯿﻦ.
]٢[د ﺣﯿﺚ د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ اﺳﺘﺨﺪم)س= (س٢
ﺣﯿﺚ ع ، ر اﻟﺪاﻟﺘﯿﻦ ﻣﻦ ﻛﻞ ﻟﺘﻤﺜﯿﻞ:
)أ(ر)س= (س٢
+١)ب(ع)س= (س ــ٢
ــ٢
اﻟﺪاﻟﺔ ﻣﺪى ﻋﯿﻦ و اﻟﻤﻨﺤﻨﻰ رأس ﻧﻘﻄﺔ ﻋﯿﻦ اﻟﺮﺳﻢ وﻣﻦ.](https://image.slidesharecdn.com/2017-160826233717/85/2017-52-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٣
]٣[د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ارﺳﻢ)س= (س٢
ــ٦س+٩أ ﺛﻢ، اﻟﻤﻨﺤﻨﻰ رأس اﻟﺮﺳﻢ ﻣﻦ وﺟﺪ
اﻟﺘﻤﺎﺛﻞ ﻣﺤﻮر ﻣﻌﺎدﻟﺔ ، اﻟﺪاﻟﺔ ﻧﻮع اﻻطﺮاد ، اﻟﻤﺪى
]٤[اﻟﺘﻤﺎﺛﻞ ﻣﺤﻮر ﻣﻌﺎدﻟﺔ و اﻟﻨﻮع و اﻻطﺮاد و اﻟﻤﺪى ﻋﯿﻦ ﺛﻢ اﻵﺗﯿﺔ اﻟﺪوال ﻣﻦ ﻛﻞ ارﺳﻢ.
)١(د)س= (س٢
ــ١)٢(د)س= (١س ــ٢
)٣(د)س) = (ــ س١(٢
)٤(د)س) = (س–٢(٢
)٥(د)س) = (س–٢(٢
+١
)٦(د)س= (ــ)ــ س١(٢
)٧(د)س= (١ــ)س–١(٢
)٨(د)س= (س٢
+١)٩(د)س= (ــ٤ــ)س–١(٢
)١٠(د)س= (س٢
د ﺣﯿﺚ] :-١،٣[Cح
)١١(د)س) = (س+٢(٢
ــ٢)١٢(د)س= (س٢
ــ٤س+٤
)١٣(د)س= (س٢
ــ٤س+١)١٤(د)س= (س|س|
)١٥(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﺗﺪرﯾﺐاﻟﺪاﻟ ﻋﻠﻰاﻟﺘﻜﻌﯿﺒﯿﺔ ﺔ:
]١[](https://image.slidesharecdn.com/2017-160826233717/85/2017-53-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٤
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٢[
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٣[
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﺗﺪرﯾﺐﻋﻠاﻟﻜﺴﺮﯾﺔ اﻟﺪاﻟﺔ ﻰ:
]١[اﺑﺤﺚ و داﻟﺔ ﻛﻞ ﻣﺪى و ﻣﺠﺎل أوﺟﺪ اﻟﺮﺳﻢ ﻣﻦ و اﻻﺗﯿﺔ ﺑﺎﻟﻘﻮاﻋﺪ اﻟﻤﻌﺮﻓﺔ اﻟﺪوال ﻣﻦ ﻛﻼ ﻣﺜﻞ
ذﻟﻚ ﻏﯿﺮ أو زوﺟﯿﺔ أو ﻓﺮدﯾﺔ ﻛﻮﻧﮭﺎ ﺣﯿﺚ ﻣﻦ ﻧﻮﻋﮭﺎ و اطﺮادھﺎ:
١(د)س() =٢(د)س) = (٣(د)س+ = (٣
٤(د)س) = (٥(د)س) = (٦(د)س= (
٧(د)س) = (٨(د)س) = (٩(د)س= (
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٢[
-٢
س
٢
س
١
س
١
س+٣
١
س-٣
٢س+٤
س-٣
١
|س+٣|
)س–٢(٢
|)س–٢(٣
|
٣س-١
س](https://image.slidesharecdn.com/2017-160826233717/85/2017-54-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٥
]٣[
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٤[
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ](https://image.slidesharecdn.com/2017-160826233717/85/2017-55-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٦
اﻟﻤﺘﺒﺎﯾﻨﺎت و اﻟﻤﻌﺎدﻻت ﺣﻞ
أوﻻ:اﻟﻤﻌـــﺎدﻻت ﺣـﻞ:
*أن ﺗﺬﻛﺮ:
)اﻟﻤﻘﯿﺎس ﻣﻔﮭﻮم(ﺳﺎﻟﺐ ﻏﯿﺮ ﺣﻘﯿﻘﻰ ﻋﺪد ھﻮ)٠(
)اﻟﻌــﺪد ﻣﻘﯿﺎس(اﻟﻌﺪد ھﺬا ﻟﻤﺮﺑﻊ اﻟﻤﻮﺟﺐ اﻟﺘﺮﺑﯿﻌﻰ اﻟﺠﺬر ھﻮ.
ﻣﺜﻼ:|-٥|=؟٢٥=٥،|٣|=؟٩=٣،|٠|=٠،| |=
*ﺗﻌﺮﯾﻒ"ﻓﻚ"اﻟﻤﻘﯿﺎس:
|س|=|ــ س٢|=
|٢س+٦|=
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*ﺑﯿﺎﻧﯿﺎ اﻟﻤﻘﯿﺎس ﻣﻌﺎدﻻت ﺣﻞ:
د ﻟﻠﻤﻌﺎدﻟﺔ اﻟﺒﯿﺎﻧﻰ اﻟﺤﻞ١)س= (د٢)س(اﻟﺪاﻟﺘﯿﻦ ﻣﻨﺤﻨﯿﻰ ﺗﻘﺎطﻊ ﻟﻨﻘﺎط س ﻗﯿﻢ ﻣﺠﻤﻮﻋﺔ ھﻮ
ﻟﻠﺤﻞ اﻟﻌﺎﻣﺔ اﻟﻄﺮﯾﻘﺔ:
١(ﻟﻮﺣﺪه طﺮف ﻓﻰ اﻟﻤﻘﯿﺎس ﻧﺠﻌﻞ
٢(د ﻟﺘﻜﻦ و ﻣﻨﻔﺼﻠﺔ ﻛﺪاﻟﺔ اﻟﻤﻌﺎدﻟﺔ ﻣﻦ اﻷﯾﻤﻦ اﻟﻄﺮف ﻧﺮﺳﻢ)س] (ﻣﺘﻨﺎھﯿﺔ ﺑﺪﻗﺔ[
٣(ر ﻟﺘﻜﻦ و ﻣﻨﻔﺼﻠﺔ ﻛﺪاﻟﺔ اﻟﻤﻌﺎدﻟﺔ ﻣﻦ اﻷﯾﺴﺮ اﻟﻄﺮف ﻧﺮﺳﻢ)س] (ﻣﺘﻨﺎھﯿﺔ ﺑﺪﻗﺔ[
٤(س ﻗﯿﻢ ھﻰ اﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ ﻧﻜﺘﺐ و ، ر ، د اﻟﺪاﻟﺘﯿﻦ ﺗﻘﺎطﻊ ﻟﻨﻘﻂ اﻟﺴﯿﻨﯿﺔ اﻹﺣﺪاﺛﯿﺎت ﻧﺤﺴﺐ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
١
٢
١
٢
سس ،٠
-سس ،>٠
س-٢س ،٢
-س+٢س ،>٢
٢س+٦س ،-٣
-٢س–٦س ،>-٣](https://image.slidesharecdn.com/2017-160826233717/85/2017-56-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٧
س–٣–٥،س٣
-س+٣-٥س ،>٣
س–٨س ،٣
-ــ س٢س ،>٣
٣س ﻋﻨﺪﻣﺎ س ــ<١
ﻣﺜﺎل:د اﻟﺪاﻟﺔ ارﺳﻢ)س= (
١+ﻋﻨﺪﻣ سس ﺎY١
د ﺗﺠﻌﻞ اﻟﺘﻰ س ﻗﯿﻢ أوﺟﺪ ﺛﻢ)س= (٠
اﻟﺤﻞ:
س<١سY١
د)س= (٠س ﻋﻨﺪ=٣س ،=-١
م.ح=}٣،-١{
اﻟﺠﺒﺮى اﻟﺘﺤﻘﻖ:
د ﺣﯿﺚ)س= (٠
س ﻋﻨﺪﻣﺎ<١ﻓﺈن٣س ــ=٠Bس=٣g[١،∞]اﻟﻤﻌﻄﺎة اﻟﻔﺘﺮة ﺗﺤﻘﻖ
س ﻋﻨﺪﻣﺎY١ﻓﺈن١+س=٠Bس=ــ١g[-∞،-١]اﻟﻤﻌﻄﺎة اﻟﻔﺘﺮة ﺗﺤﻘﻖ
د اﻟﻤﻌﺎدﻟﺔ ﺣﻞ ﻣﺠﻤﻮﻋﺔ)س= (٠ھﻰ}٣،-١{
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]١[اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|ــساب ــ|=ﺣـ:
ﻣﺜﺎل:اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|س–٣|=٥ﺟﺒﺮﯾﺎ اﻟﻨﺎﺗﺞ وﺣﻘﻖ ﺑﯿﺎﻧﯿﺎً ً
اﻟﺒﯿﺎﻧﻰ اﻟﺤﻞ:اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻌﺎدﻟﺔ ﻧﻀﻊ:|س–٣|-٥=٠
د أن ﻧﻔﺮض)س= (|س–٣|-٥
=
د)س= (
س٤٣٢١٠-١
د)س(-١٠١٢١٠
ص′
ص
٠
سس′
)٣،-٥(
٨٣-٢](https://image.slidesharecdn.com/2017-160826233717/85/2017-57-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٨
ﻓﻰ اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﯾﻘﻄﻊ اﻟﻤﻨﺤﻨﻰ اﻟﺮﺳﻢ ﻣﻦ)٨،٠(،)-٢،٠(
م.ح=}٨،-٢{
اﻟﺠﺒﺮى اﻟﺤﻞ:
س ﻋﻨﺪﻣﺎ٣ﻓﺈنس-٨=٠س=٨g]٣،∞]
ﻋﻨﺪﻣﺎس>٣ﻓﺈن–س–٢=٠س=-٢g[-∞،٣]
اﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ=}٨،-٢{
أﺧﺮ ﺣﻞ:ﻧﺮﺳﻢ:د)س= (|س–٣|ر ،)س= (٥
ر اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ)س(د اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ ﯾﻘﻄﻊ)س(
اﻟﻨﻘﺎط ﻓﻰ)٨،٥(،)-٢،٥(
م.ح=}٨،-٢{
اﻟﺠﺒﺮى اﻟﺤﻞ:
|س–٣|=٥
Bس–٣=±٥
Bس–٣=٥س–٣=-٥
س=٨س ﺗﺤﻘﻖ=-٢ﺗﺤﻘﻖ
Bم.ح=}٨،-٢{
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|س|+١=٠ﺟﺒﺮﯾﺎ و ﺑﯿﺎﻧﯿﺎ
اﻟﺒﯿﺎﻧﻰ اﻟﺤﻞ:
د ﻧﺮﺳﻢ)س= (|س|+١=
اﻟﺴﯿﻨﺎت ﻣﺤﻮر ﯾﻘﻄﻊ ﻻ اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰBم.ح=Ø
اﻟﺠﺒﺮى اﻟﺤﻞ:
س ﻋﻨﺪﻣﺎX٠س ﻓﺈن+١=٠Bس=-١h]٠،∞]
ﻋﻨﺪﻣﺎس>٠ﻓﺈن–س+١=٠Bس=١h[-∞،٠]
-١،١اﻟﻤﻌﺎدﻟﺔ ﯾﺤﻘﻖ ﻻBم.ح=Ø
ﺻﺺ
ﺳﺲ
ﺳﺲ′
ﺻﺺ′
)٣،٠(-٢
٥
٠
٨
س+١س ﻋﻨﺪﻣﺎX٠
-س+١س ﻋﻨﺪﻣﺎ>٠
ﺳﺲ
١
ﺻﺺ
٠-١ ١](https://image.slidesharecdn.com/2017-160826233717/85/2017-58-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٥٩
ﺟﺒﺮى ﺣﻞآﺧﺮ:A|س|+١=٠B|س|=-١ﻻن ﻣﺮﻓﻮض|س|X٠
Bم.ح=Ø
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٢[اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|اس+ب|=س ﺟـ+ء:
ﻣﺜﺎل:اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|٢س–٣|=س+٣ﺟﺒﺮﯾﺎ و ﺑﯿﺎﻧﯿﺎ
اﻟﺒﯿﺎﻧﻰ اﻟﺤﻞ:د اﻟﺪاﻟﺘﯿﻦ ﻧﺮﺳﻢ)س= (|٢س–٣|
ر ،)س= (س+٣
اﻟﺪاﻟﺘﯿﻦ ﻣﻨﺤﻨﯿﻰ ﺗﻘﺎطﻊ ﻧﻘﻂ ﻧﺠﺪ اﻟﺮﺳﻢ ﻣﻦ و
)٠،٣(،)٦،٩(
Bاﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ=}٠،٦{
اﻟﺠﺒﺮى اﻟﺤﻞ:
س ﻋﻨﺪﻣﺎX١ .٥
ﻓﺈن٢س–٣=س+٣
Bس=٦g]١.٥،∞]ﺗﺤﻘﻖ
س ﻋﻨﺪﻣﺎ>١.٥
ﻓﺈن–٢س+٣=س+٣
B–٣س=٠
Bس=٠g[-∞،١.٥]ﺗﺤﻘﻖ
Bاﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ=}٠،٦{
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|٢س+٥|=س–٤ﺑﯿﺎﻧﯿﺎﺟﺒﺮﯾﺎ و
اﻟﺒﯿﺎﻧﻰ اﻟﺤﻞ:د اﻟﺪاﻟﺘﯿﻦ ﻧﺮﺳﻢ)س= (|٢س+٥|ر ،)س= (س–٤
ﻟﻠﻤﻨﺤﯿﯿﻦ ﺗﻘﺎطﻊ ﻧﻘﻂ ﯾﻮﺟﺪ ﻻ اﻧﮫ ﻧﻼﺣﻆ
Bاﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ=Ø
اﻟﺠﺒﺮى اﻟﺤﻞ:
س ﻋﻨﺪﻣﺎX–٢.٥B٢س+٥=س–٤
Bس=-٩h]-٢.٥،∞]ﺗﺤﻘﻖ ﻻ
س ﻋﻨﺪﻣﺎ>-٢.٥B–٢س–٥=س–٤
B–٣س=١Bس=-h[-∞،-٢.٥]ﺗﺤﻘﻖ ﻻ
Bاﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ=Ø
٤)-٢.٥،٠(
-٤
٥
ﺻﺺ
ﺳﺲ
١
٣](https://image.slidesharecdn.com/2017-160826233717/85/2017-59-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٦٠
]٣[اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|سا+ب|=|س ج+ء|:
ﻣﺜﺎل:اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|س–٢|=|س+٣|ﺟﺒﺮﯾﺎ اﻟﻨﺎﺗﺞ وﺣﻘﻖ ﺑﯿﺎﻧﯿﺎً ً
اﻟﺒﯿﺎﻧﻰ اﻟﺤﻞ:
د ﻧرﺳم١=|س–٢|
د ،٢=|س+٣|
ھﻰ اﻟﺘﻘﺎطﻊ ﻧﻘﻄﺔ أن ﻧﺠﺪ)-٠.٥،٢.٥(
اﻟﺠﺒﺮى اﻟﺤﻞ:
اﻟطرﻓﯾن ﺑﺗرﺑﯾﻊ) :|س–٢|(٢
) =|س+٣|(٢
)س–٢(٢
) =س+٣(٢
س٢
-٤س+٤=س٢
+٦س+٩
-١٠س=٥
س= =اﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ={ }
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|س–٢|+|س–١|=٣وﺟﺒﺮﯾﺎ ﺑﯿﺎﻧﯿﺎ
اﻟﺒﯿﺎﻧﻰ اﻟﺤﻞ:ﻟﻠﻤﻌﺎدﻟﺔ اﻟﺘﻌﺮﯾﻒ ﺑﺎﻋﺎدة|س–٢|=-|س–١|+٣
د اﻟﺪاﻟﺘﯿﻦ ﻧﺮﺳﻢ)س= (|س–٢|ر ،)س= (-|س–١|+٣
اﻟﻤﻨﺤﻨﯿﻦ ﺗﻘﺎطﻊ ﻧﻘﻂ اﻟﺮﺳﻢ ﻣﻦ
ھﻰ)٣،١(،)٠،٢(
Bاﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ=}٠،٣{
اﻟﺠﺒﺮى اﻟﺤﻞ:ﻟﻠﻤﻌﺎدﻟﺔ اﻟﺘﻌﺮﯾﻒ ﺑﺎﻋﺎدة
م.ح=}٠،٣{
س–٢
س–١
-٣
س=٣
-س+٢
س–١
-٣
-٢
ﻣﺮﻓﻮض
-س+٢
-س+١
-٣
س=٠
ص
)٢،٠(
س′
ص′
س
)-٣،٠( )-٠.٥،٠(
د١
د٢
٢.٥
-٥
١٠
-١
٢
-١
٢
-٢ -١ ١ ٢ ٣ ٤
٤
٣
٢
١
-١
-٢
-٣
١ ٢](https://image.slidesharecdn.com/2017-160826233717/85/2017-60-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٦١
ﻣﺜﺎل:اﻟﻤﻌﺎدﻟﺔ ﺣﻞ ﻣﺠﻤﻮﻋﺔ أوﺟﺪ|ــ س٢|+|س|=١ﺑﯿﺎﻧﯿﺎ
اﻟﺤﻞ:
اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻌﺎدﻟﺔ ﻧﻀﻊ:
|ــ س٢|=١ــ|س|
د اﻟﺪاﻟﺘﯿﻦ ﻧﺮﺳﻢ١)س= (|س–٢|
د ،٢)س= (١ــ|س|
اﻟﺮﺳﻢ ﻣﻦ:اﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ=Z
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻟﻤﻌﺎدﻟﺔ ﺣﻞ|س–٢|+|س|=٤ﺑﯿﺎﻧﯿﺎ
اﻟﺤﻞ:
اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻌﺎدﻟﺔ ﻧﻀﻊ:
|ــ س٢|=٤ــ|س|
د اﻟﺪاﻟﺘﯿﻦ ﻧﺮﺳﻢ١)س= (|س–٢|
د ،٢)س= (٤ــ|س|
اﻟﺮﺳﻢ ﻣﻦ:اﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ=}-١،٣{
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﺑﯿﺎﻧﯿﺎ ﻟﻠﻤﻌﺎدﻟﺔ اﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ أوﺟﺪ|س+٢|+|س|=٢
اﻟﺤﻞ:
اﻟﺼﻮرة ﻋﻠﻰ اﻟﻤﻌﺎدﻟﺔ ﻧﻀﻊ
|س+٢|=٢ــ|س|
د ﻧﺮﺳﻢ١)س= (|س+٢|د ،٢)س= (٢ــ|س|
ﻓﻨﺠﺪ اﻟﺒﯿﺎﻧﯿﯿﻦ اﻟﺸﻜﻠﯿﻦ ﺗﻘﺎطﻊ ﻧﻘﻂ ﻧﻮﺟﺪ:
م.ح] =-٢،٠[
-٣ -٢ -١ ١ ٢ ٣ ٤
٤
٣
٢
١
-١
-٢
-٣
-٣ -٢ -١ ١ ٢ ٣ ٤
٤
٣
٢
١
-١
-٢
-٣
-٣ -٢ -١ ١ ٢ ٣ ٤
٤
٣
٢
١
-١
-٢
-٣
](https://image.slidesharecdn.com/2017-160826233717/85/2017-61-320.jpg)




![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٦٩
اﻟﺤﻞ:
)١(|س–٥> |٢
س إﻣﺎ–٥>٢Gس>٢+٥Gس>٧
أو-)ـ س٥(>٢Gس–٥<-٢Gس<٣
Bم.ح[ =٣،٧]
)٢(|٢س+٣|Y٥
إﻣﺎ٢س+٣Y٥G٢سY٥–٣G٢سY٢GسY١
ــ أو)٢س+٣(Y٥G٢س+٣X–٥G٢سX–٨GسX-٤
Bسg]-٤،١[
)٣(|٣س–٤< |٥
إﻣﺎ٣س–٤<٥G٣س<٩Gس<٣
ــ أو)٣س–٤(<٥G٣س–٤>-٥G٣س>-١Gس>
Bم.ح=ــ ح]،٣[
)٤(|س+٧|X٠
س إﻣﺎ+٧X٠GسX–٧
ــ أو)س+٧(X٠Gس+٧Y٠GسY–٧
Bم.ح=ح
ﻣﻼﺣﻈﺔ:اﻟﻤﺘﺒﺎﯾﻨﺔ ﺣﻞ ﻣﺠﻤﻮﻋﺔ أوﺟﺪ اﻟﻄﺎﻟﺐ ﻋﺰﯾﺰ|س+٧> |٠ﻋﻦ اﻟﻔﺮق ﻻﺣﻆ و)٤(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻵﺗﯿﺔ اﻟﻤﺘﺒﺎﯾﻨﺎت ﻣﻦ ﻛﻞ ﺣﻞ ﻓﺘﺮة ﺻﻮرة ﻋﻠﻰ أوﺟﺪ:
١(؟س٢
ـ"ـ٨"س"+"١٦">٣٢(|٥–٣س|X٢
٣(|٢س–٣< |٩-|٦–٤س|
-١
٣ -١
٣](https://image.slidesharecdn.com/2017-160826233717/85/2017-69-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧٠
اﻟﺤﻞ:
)١(؟س٢
"–٨"س"+"١٦"">٣G؟)س""–٤"(٢
">٣G|س–٤> |٣
س إﻣﺎ–٤>٣Gس>٣+٤Gس>٧
،أ-)س–٤(>٣Gس–٤<-٣Gس<١
Bسg[١،٧]
)٢(|٥–٣س|X٢G|٣س–٥|X٢
إﻣﺎ٣س–٥X٢G٣سX٧GسX
،أ-)٣س–٥(X٢G٣س–٥Y-٢G٣سY٣GسY١
Bسgح-[١،]
)٣(|٢س–٣< |٩-|٦–٤س|G|٢س–٣< |٩-|٤س–٦|
G|٢س–٣< |٩–٢|٢س–٣|G|٢س–٣|+٢|٢س–٣< |٩
G٣|٢س–٣<|٩G|٢س–٣<|٣
إﻣﺎ٢س–٣<٣G٢س<٦Gس<٣
،أ-)٢س–٣(<٣G-٢س+٣<٣G–٢س<٠Gس>٠
Bم.ح=ح-]٠،٣[
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻟﻤﺘﺒﺎ ﺣﻞﯾﻨﺔ:|٣س-٤|٥
اﻟﺤﻞ:٣س-٤٥٣س-٤-٥
٣س٩٣س-١
س٣س
م.ح] =٣،]م.ح[ =-،[
م.ح] =٣،]ﺑﻶ[-،[
م.ح=ح-[،٣]
٧
٣
٧
٣
-١
٣
-١
٣
-١
٣
-١
٣](https://image.slidesharecdn.com/2017-160826233717/85/2017-70-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧١
اﻟﻤﺘﺒﺎﯾﻨﺎ و اﻟﻤﻌﺎدﻻت ﺣﻞ ﻋﻠﻰ ﺗﻤﺎرﯾﻦت
]١[اﻵﺗﯿﺔ اﻟﻤﻌﺎدﻻت ﻣﻦ ﻟﻜﻞ اﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ ﺟﺒﺮﯾﺎ أوﺟﺪ:
أ(٢|س+١|-٥=٠ب(٢|س+٥|=٤+س
ﺟـ(٣|س–١|-٢|٢–س|=٠د(؟س٢
"–٤"س"+"٤"=٤
]٢[
]٣[
]٤[
١(
٢(
٣(
٤(
٥(
٦(
٧(
٨(
٩(
١٠(
١١(
١٢(](https://image.slidesharecdn.com/2017-160826233717/85/2017-71-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧٣
أن ﺗﺬﻛﺮ:
)١(ﻛﺎن إذا:اgﺣﺢ،نgﺻﺺ+
ﻓﺈن:ان
=ا×ا×ا×ا×٠٠٠×ا
ﺣﯿﺚاﻛﻌ ﻣﻜﺮرﺎﻣﻞناﻟﺮﻣﺰ و اﻟﻤﺮات ﻣﻦان
ﯾﻘﺮا:اأسن
ﻟﻠﻌﺪد اﻟﻨﻮﻧﯿﺔ اﻟﻘﻮة ،أاﻟﻸﺳﺎس ،أا
ﻣﺜﻼ:]٢ة٥[٤٤
=٢$×]ة٥[$=١٦×٢٥
)٢(اﺻﻔﺮ
=١ﺑﺸﺮطا}٠ﻻن)ﺻﻔﺮ(ﺻﻔﺮ
ﻣﻌ ﻏﯿﺮﺮف
ﺚﻣﻣﺜﻼ]-٧[ﺻﻔﺮ
=١،٥ص
=١ص ﻓﺈن=ﺻﻔﺮ
)٣(ﻛﺎن إذااﺣﻘﯿﻘﻰ ﻋﺪد}، ﺻﻔﺮﻧﻦﻣﻮﺟﺐ ﺻﺤﯿﺢ ﻋﺪد
ﻓﺈن:اﻧﻦ
=،ا-ﻧﻦ
=
ﻣﺜﻼ:٣٤
==٨١،٧–٢
=
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﻼﺣﻈﺎت:
١-اﻟﻌﺪداﻧﻦ
ﻟﻠﻌﺪد ﺿﺮﺑﻰ ﻣﻌﻜﻮسا-ﻧﻦ
أن ﺣﯿﺚ:اﻧﻦ
×ا-ﻧﻦ
=اﺻﻔﺮ
=١
ﻣﺜﻼ:٣–٥
×٣٥
=١،]ة٥[٤
×]ة٥[-٤
=١
٢-[ ]ﻧﻦ[ ] =-ﻧﻦ
ﻣﺜﻼ:[ ]-٤
[ ]=٤=
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻷﺳﺲ ﻗﻮاﻧﯿﻦ) :ح ﻓﻰ اﻟﺼﺤﯿﺤﺔ اﻟﻘﻮى ﻗﻮاﻧﯿﻦ(
ﻛﺎن إذا:ـ ا،بgﺣﺢ،نgﺻﺺﻓﺈن:
١-ام
×ان
=ام+ن
ﻣﺜﻼ٧٣
×٧٢
=٧٥
،]ة٣[٣
×]ة٣]= [ة٣[٤
=٩
٢-ام
÷ان
=ام-ن
ﻣﺜﻼ٣٧
÷٣٣
=٣٧–٣
=٣٤
=٨١
،]-ة٥[١٥
÷]-ة٥[١٢
]=-ة٥[٣
=-٥ة٥
ﺔ ﻴ ﻧ ﺎ ﺜ ﻟ ا ة ﺪ ﺣ ﻮ ﻟ ا
ﻋﻠﯿﮭﺎ ﺗﻄﺒﯿﻘﺎت و اﻟﻠﻮﻏﺎرﯾﺘﻤﺎت و اﻷﺳﺲ
١
ﺍ-ﻦﻧ
١
ﺍﻦﻧ
١
٣-٤
١
٧@
ا
ب
ب
ا
٢
٣
٣
٢
١٦
٨١](https://image.slidesharecdn.com/2017-160826233717/85/2017-73-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧٤
٣-]ب ا[ن
=ان
×بن
ﻣﺜﻼ١٥ن
]=٣×٥[ن
=٣ن
×٥ن
٤-]ا÷ب[ن
=ان
÷بن
ﻣﺜﻼ[ ]ن
=،[ ]=ن
٥-]ام
[ن
=انم
ﻣﺜﻼ]س٣
[٢
=س٦
،ـ]٣٢
[س
=٣٢س
ﻣﻼﺣﻈﺎت:
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﺻﻮرة ﻻﺑﺴﻂ اﺧﺘﺼﺮ:
اﻟﺤﻞ= = :
=٥٣ن+١–٣ن
×٣٣ن–٣ن
=٥×٣٠
=٥×١=٥
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﻗﯿﻤﺔ ﺻﻮرة اﺑﺴﻂ ﻓﻰ أوﺟﺪ
اﻟﺤﻞ:اﻟﻤﻘﺪار==
=٣–٩+٢+٨
×٢٤–٤
=٣١
×٢ﺻﻔﺮ
=٣×١=٣
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:إذاﻛﺎن٣س+١
+٣س-١
=١٠س ﻗﯿﻤﺔ ﻓﺄوﺟﺪ
اﻟﺤﻞ:
٣س+١
+٣س-١
=٣س-١
]٢
٣+١= [٣س-١
]٩+١[=٣س-١
×١٠=١٠
B٣س–١
=١Bس–١=٠Bس=١
آﺧﺮ ﺣﻞ:٣س
)٣+٣–١
= (١٠G٣س
×=١٠G٣س
=١٠×=٣
٥
٧
٣
٥
٣ن
٥ن
٥ن
٧ن
)١) (ا+ب(ن
}ان
+بن
،)ا-ب(ن
}ان
-بن
)٢) (-ا(ن
=ان
)ﺣﯿﺚنزوﺟﻰ ﻋﺪد(ﻣﺜﻼ)-٣(٤
=٣٤
=٨١
)٣) (-ا(ن
=-ان
)ﺣﯿﺚنﻓﺮدى ﻋﺪد(ﻣﺜﻼ)-٣(٣
=-٣٣
=-٢٧
٥٣ن+١
×٢٧ن
١٥٣ن
٥٣ن+١
×]٣٣
[ن
]٣×٥[٣ن
٥٣ن+١
×٣٣ن
٣٣ن
×٥٣ن
٥٣ن+١
×٢٧ن
١٥٣ن
)٢٧(-٣
×)١٢(٢
١٦×)٨١(-٢
)٣٣
(-٣
×)٣×٢٢
(٢
٢٤
×)٣٤
(-٢
٣-٩
×٣٢
×٢٤
٢٤
×٣-٨
١٠
٣
٣
١٠](https://image.slidesharecdn.com/2017-160826233717/85/2017-74-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧٥
ﻣﺜﺎل:أن أﺛﺒﺖ=
اﻟﺤﻞ:اﻷﯾﻤﻦ اﻟﻄﺮف= =
= =÷٥=×= =اﻷﯾﺴﺮ اﻟﻄﺮف
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻟﺼﺤﯿﺤ اﻻﺟﺎﺑﺔ اﺧﺘﺮﺔ:
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﻼﺣﻈﺎت:
١(أوﻟﯿﺎ ﻋﺪدا اﻷﺳﺎس ﺟﻌﻞ ﻣﻦ ﻻﺑﺪ اﻷﺳﺲ ﻣﺴﺎﺋﻞ ﺣﻞ ﻋﻨﺪ)٢،٣،٥،٧،١١،( .....
٢(ﻛﺎﻧﺖ إذا٧٢س
+٤×٧س
ﻓﺮض ﯾﻤﻜﻦ٧س
=صBص٢
+٤ص
٣(ﻛﺘﺎﺑﺘﮫ ﯾﻤﻜﻦ اﻟﻜﺴﺮ ﻛﺎن إذا٣س+س ــ ص
×٧٥ــ٢ــ س١
اﻟﻜﺴﺮ ﺷﺮطﺔ ﻋﻦ ﻧﺴﺘﻐﻨﻰ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻟﻨﻮﻧﯿﺔ اﻟﺠﺬور:
س اﻟﻤﻌﺎدﻟﺔ٢
=٩ھﻤﺎ ﺣﻘﯿﻘﯿﺎن ﺟﺬران ﻟﮭﺎ٣،-٣
س اﻟﻤﻌﺎدﻟﺔ٣
=٨ھﻮ وﺣﯿﺪ ﺣﻞ ﻟﮭﺎ٢)ﻣﺮﻛﺒﺔ اﻋﺪاد اﻟﺠﺬور ﺑﺎﻗﻰ و(ھﻜﺬا و.....
ﻋﺎم ﺑﻮﺟﺔ:س اﻟﻤﻌﺎدﻟﺔن
=اﺣﯿﺚاgح.نgص+
ﻟﮭﺎناﻟﺠﺬور ﻣﻦ
ﻟﻠﻤﻌﺎدﻟﺔ اﻟﻤﺨﺘﻠﻔﺔ اﻟﺤﺎﻻتسن
=ا:
]١[، زوﺟﯿﺎ ن ﻛﺎن إذااﻣﻮﺟﺒﺎ:
ﺳﺎﻟﺐ اﻵﺧﺮ و ﻣﻮﺟﺐ أﺣﺪھﻤﺎ ﺣﻘﯿﻘﯿﺎن ﺟﺬران ﻟﮭﺎ اﻟﻤﻌﺎدﻟﺔ ﻓﺈن)ﻣﺮﻛﺒﺔ أﻋﺪاد اﻟﺠﺬور ﺑﺎﻗﻰ(
٥×٣٢ن
-٤×٣٢ن-١
٢×٣٢ن+١
-٣٢ن
١١
١٥
٥×٣٢ن
-٢٢
×٣٢ن-١
٣٢ن
)٢×٣–١(
٣٢ن
)٥–٢٢
×٣–١
(
٣٢ن
)٢×٣–١(
٥ــ
٥
٤
٣١١
٣
١١
٣
١
٥
١١
١٥
٣س
×٧٥
×٣ص
٧س
×٣٢س+١](https://image.slidesharecdn.com/2017-160826233717/85/2017-75-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧٦
ﻟﮭﻤﺎ ﯾﺮﻣﺰ ون
؟اــ ،ن
؟اوﻟﻠﻌﺪد اﻟﻤﻮﺟﺐ اﻟﻨﻮﻧﻰ اﻟﺠﺬر ﯾﺴﻤﻰااﻟﻨﻮﻧﻰ ﺑﺎﻟﺠﺬر
ﻟﻠﻌﺪد اﻵﺳﺎﺳﻰا
ﻣﺜﻼ:س اﻟﻤﻌﺎدﻟﺔ٤
=٨١ھﻤﺎ ﺟﺬران ﻟﮭﺎ٤
؟٨١"=٣ــ ،٤
؟٨١=ــ٣
]٢[، زوﺟﯿﺎ ن ﻛﺎن إذااﺳﺎﻟﺒﺎ:س اﻟﻤﻌﺎدﻟﺔن
=اﺣﻘﯿﻘﯿﺔ ﺟﺬور ﻟﮭﻞ ﻟﯿﺲ]ﺗﺨﯿﻠﯿﺔ ﺣﺬورھﺎ[
ﻣﺜﻼ:اس ﻟﻤﻌﺎدﻟﺔ٤
=-١٦ﺣﻘﯿﻘﯿﺔ ﺟﺬور ﻟﮭﺎ ﻟﯿﺲ]ﺗﺨﯿﻠﯿﺎن ﺟﺬران ﻟﮭﺎ٤، ت-٤ت[
]٣[ﻛﺎن إذان، ﻓﺮدﯾﺎاgح:
س اﻟﻤﻌﺎدﻟﺔ ﻓﺈنن
=اھﻮ وﺣﯿﺪ ﺣﻘﯿﻘﻰ ﺟﺬر ﻟﮭﺎن
؟ا)ﻣﺮﻛﺒﺔ أﻋﺪاد اﻟﺠﺬور ﺑﺎﻗﻰ(
ﻣﺜﻼ:س اﻟﻤﻌﺎدﻟﺔ٥
=ــ٣٢ھ وﺣﯿﺪ ﺣﻘﯿﻘﻰ ﺟﺬر ﻟﮭﺎﻮ٥
؟ــ٣٢"=-٢
]٤[إذﻛﺎن انgص+
،ا=ﺻﻔﺮ:
س اﻟﻤﻌﺎدﻟﺔ ﻓﺈنن
=ﺻﻔﺮ ھﻮ وﺣﯿﺪ ﺣﻘﯿﻘﻰ ﺣﻞ ﻟﮭﺎ ﺻﻔﺮ
ﻣﺜﻼ:س اﻟﻤﻌﺎدﻟﺔم
=س ﻓﺈن ﺻﻔﺮ=ﺻﻔﺮ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﻓﻰ أوﺟﺪحاﻵﺗﯿﺔ اﻟﻤﻌﺎدﻻت ﻣﻦ ﻛﻞ ﺣﻞ ﻣﺠﻤﻮﻋﺔ:
)أ(س٤
=١٦)ب(س٥
=٢٤٣
اﻟﺤﻞ) :أ(س٤
=١٦Bس=±؟١٦"=±٢)ﻣﺮﻛﺒﺔ اﻋﺪاد اﻟﺠﺬور ﺑﺎﻗﻰ و(
Bم.ح=}٢،-٢{
)ب(س٥
=٢٤٣Bس=٥
؟٢٤٣"=٣)ﻣﺮﻛﺒﺔ اﻋﺪاد اﻟﺠﺬور ﺑﺎﻗﻰ و(
Bم.ح=}٣{
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻟﻜﺴﺮﯾﺔ اﻷﺳـﺲ:
ﻣﺜﻼ:؟ا)=ا(،؟٣) =٣(،٣
؟ا)=ا(،٣
؟٧) =٧(
ﻋﺎم ﺑﻮﺟﺔ:ن
؟ا=ا،ن
؟ان
"=ا=اﯾﺮاﻋﻰنﻓﺮدى أو زوﺟﻰ
ﻣﻼﺣﻈﺔ] :١[ن
؟ان
=|ا|ﻛﺎن إذانزوﺟﻰ]ﻣﺜﻼ٤
؟١٦=٤
؟|-٢"|٤
"=٤
؟|٢|٤
"=٢[
]٢[ن
؟ان
=اﻛﺎن إذانﻓﺮدى]ﻣﺜﻼ٥
؟٣٢"=٢،٥
؟-٣٢"=-٢[
١
٢
١
٢
١
٣
٢
١
٣
٢ ١
ن
ن
ن](https://image.slidesharecdn.com/2017-160826233717/85/2017-76-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧٧
*اﻟﻨﻮﻧﯿﺔ اﻟﺠﺬور ﺧﻮاص:
ﻛﺎن إذان
؟ا،ن
؟بgح،اgح-}٠{ن ،gص+
ــ}١{م ،gصﻓﺈن:
]١[ن
؟ب ا"=ن
؟ا×ن
؟بﻣﺜﻼ٣
؟٥×"٣"=٣
؟٥×٣
؟٣،٧
؟٢×٧
؟٣=٧
؟٦
]٢[ن
ﰈﱂ=ب ،}٠ﻣﺜﻼ٥
ﰈﱂ=،=٣
ﰈﱂ=٣
ﰈ
]٣[ن
؟ام
=)ن
؟ا(م
=اﻣﺜﻼ٥
؟س٢
") =٥
؟س(٢
) =س(
ﻣﻠﺤﻮظﺔ:اﻟﺼﺤﯿﺤﺔ اﻻﺳﺲ ﻗﻮاﻧﯿﻦ ﻟﻨﻔﺲ ﺗﺨﻀﻊ اﻧﮭﺎ ﺣﯿﺚ اﻟﻜﺴﺮﯾﺔ اﻷﺳﺲ ﻗﻮاﻧﯿﻦ ﺗﻌﻤﯿﻢ ﯾﻤﻜﻦ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:أوﺟﺪ)أﻣﻜﻦ إن(ﻣﻦ ﻛﻞ ﻗﯿﻤﺔ:
]١[ــ؟٣٦"]٢[ــ)٨١] (٣) [ــ١٢٥(
]٤[|٧
؟ـ١٢٨"|]٥) [-٩] (٦) [ــ٢٥(
اﻟﺤﻞ:
]١[ــ؟٣٦"=ــ؟٦٢
=ــ٦
]٢[ــ)٨١= (ــ) ]٣٤
= [ (٣=٣
]٣) [ــ١٢٥) ] = (-٥(٣
) = [-٥(
]٤[|٧
؟ـ١٢٨"|=|٧
؟)-٢("
٧
|=|-٢|=٢
]٥) [-٩= (؟-٩hح]٦) [-٢٥= (٤
؟-٢٥"hح
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﻣﻦ ﻛﻞ ﺻﻮرة أﺑﺴﻂ ﻓﻰ أوﺟﺪ:
]١[ــ٣
؟٨ا٦
"ب٩
"]٢[٤
؟١٦"س"
٤
"ص"
٨
"]٣[٤
؟١٦"ا١٢
"]٤[٦
؟)س"+"٢"ص"(١٨
"
اﻟﺤﻞ] :١[ــ٣
؟٨ا٦
"ب٩
"=ــ٣
؟٨×٣
؟ا٦
×٣
؟ب٩
=ــــ٢ا×ب=-٢ا٢
ب٣
ا
ب
ن
؟ا
ن
؟ب
٣
٥
٥
؟٣
٥
؟٥
٣
؟٢
٣
؟٤
٢
٤
١
٢ م
ن
٢
٥
١
٤
٥
١
٣
٤ ١
٢
٣
١
٤
٢
١
٤
٥
١
٤
٥
٤
٤
٥ ١
٣
٤
١
٣
٤
١
٢
٣
١
٤
٢
٦
٣
١
٩
٣
١](https://image.slidesharecdn.com/2017-160826233717/85/2017-77-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧٨
]٢[٤
؟١٦"س"
٤
"ص"
٨
"=٤
؟١٦×٤
؟س٤
"×٤
؟ص٨
"=٢×|س|×|ص|٢
=٢ص س٢
]٣[٤
؟١٦"ا١٢
"=٤
؟١٦×٤
؟ا١٢
=٢×ا=٢ا٣
]٤[٦
؟)س"+"٢"ص"(١٨
") =س+٢ص) = (س+٢ص(٣
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﺻﻮرة اﺑﺴﻂ ﻓﻰ أوﺟﺪ:
اﻟﺤﻞ:اﻟﻤﻘﺪار= =
=٣+ــ
×٧ــ
=٣ﺻﻔﺮ
×٧ﺻﻔﺮ
=١×١=١
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:أ أﺛﺒﺖن=
اﻟﺤﻞ:اﻷﯾﻤﻦ اﻟﻄﺮف= =
=٧٦س–١–٦س
×٤٣س+١–٣س–١
=٧–١
×٤ﺻﻔﺮ
=×١==اﻷﯾﺴﺮ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﻛﺮة ﻗﻄﺮ ﻧﺼﻒ طﻮل ﻛﺎن إذا)ﻧﻖ(ﺑﺎﻟﻌﻼﻗﺔ ﯾﻌﻄﻰُﻧﻖ=٣
ﰈﱂﺣﺠﻤﮭﺎ ،٦٠٠ﺳﻢ٣
ﺣﯿﺚ ﻋﺸﺮﯾﺔ أرﻗﺎم ﻟﺜﻼﺛﺔ اﻟﻨﺎﺗﺞ ﻣﻘﺮﺑﺎ ﻓﺄوﺟﺪحاﻟﻜﺮة ﺣﺠﻢ:
١(اﻟﻜﺮة ﻗﻄﺮ ﻧﺼﻒ طﻮل٢(اﻟﻜﺮة ﺳﻄﺢ ﻣﺴﺎﺣﺔ
١٢
٤
١٨
٦
٣×)١٤٧(
)٦٣(
١
٢
٣
١
٦
٥ ١
٣
٦
٣×)٣×٧٢
(
)٣٢
×٧(
٣×٣×٧
٣×٧
١
٢
٣
١
٦
٥ ١
٣
٦
٢
٣
٦
١
٣
٦
١
٢
٣
١
٦
٥
١
٣
٢
١
٢
٣
١
٦
٥
٢
٣
٢
١
٣
٢
١
٣
٢
)٣٤٣(٢ــ س
×)٤(٣س+١
)١٩٦(٣س
×٤
١
٣
٢
١
٧
٣
)٧٣
(٢ــ س
×)٤(٣س+١
)٧٢
×٤(٣س
×٤
١
٣
٢
)٧(٦ــ س١
×)٤(٣س+١
)٧(٦س
×)٤(٣س
×٤
١
٧
٣
١
٧
٣
٣ح
٤π](https://image.slidesharecdn.com/2017-160826233717/85/2017-78-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٧٩
اﻟﺤﻞ:ﻧﻖ=٣
ﰈﱂ=٣
ﰈﱂﱂT٥.٢٣٢٢٣T٥.٢٣٢ﺳﻢ
اﻟﻜﺮة ﺳﻄﺢ ﻣﺴﺎﺣﺔ=٤πﻧﻖ٢
=٤×π×)٥.٢٣٢(٢
T٣٤٣.٩٨٩٦١٧٥
T٣٤٣.٩٨٩ﺳﻢ٢
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻟﻤﻌــــﺎدﻻ ﺣﻞتح ﻓﻰ اﻷﺳﯿﺔ:
ھﺎﻣﺔ ﻣﻼﺣﻈﺔ:
١(س ﻛﺎن إذا=اس ﻓﺈن=اﻓﺮدى ﻋﺪد م ﺣﯿﺚ
ﻣﺜﻼ:س=٢Bس=٢=٢٣
=٨س ،=٣
٢(س ﻛﺎن إذا=اس ﻓﺈن=±اﻋﺎﻣ ﺑﯿﻨﮭﻤﺎ ﻟﯿﺲ ن ، م ، زوﺟﻰ ﻋﺪد م ﺣﯿﺚﻣﺸﺘﺮك ﻞ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﻓﻰ اﻟﺤﻞ ﻣﺠﻤﻮﻋﺔ أوﺟﺪحاﻵﺗﯿﺔ اﻟﻤﻌﺎدﻻت ﻣﻦ ﻟﻜﻞ:
١(س=٢٧٢) (س–٢= (٢٥
٣(ــ س١٠س+٩=٠٤(ــ س٣ــ س٤=٠
٥) (س+١= (٣٢
اﻟﺤﻞ:آﺧﺮ ﺣﻞ:
]١[س=٢٧اﻟﻄﺮﻓ ﺑﺮﻓﻊﻟﻠﻘﻮة ﯿﻦ٥س=٢٧ﻟﻠﻘﻮة اﻟﻄﺮﻓﯿﻦ ﺑﺮﻓﻊ
Bس٣
) =٢٧(٥
ﻟﻠﻄﺮﻓﯿﻦ اﻟﺘﻜﻌﯿﺒﻰ اﻟﺠﺬر ﺑﺄﺧﺬBس) =٢٧) ] = (٣(٣
= [٣٥
Bس) =٣
؟٢٧(٥
=٣٥
=٢٤٣Bس=٢٤٣
Bم.ح=}٢٤٣{Bم.ح=}٢٤٣{
٣ح
٤π
٣×٦٠٠
٤π
٣
٥
٢
٢
٣
٥٢
٣
٥
٤
٣
٥
٤
٥
٥
٢
٥
٥-١
٢
-٥
٢
٣
٥
٢
٥
٣
٣
٥
٢٥
٣
٢
٥
٣
٢
م
ن
ن
م
١
٣
٣
١
٥
٣
٣
٥
م
ن
ن
م](https://image.slidesharecdn.com/2017-160826233717/85/2017-79-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٨٠
]٢) [س–٢= (٢٥ﻟﻠﻘﻮة اﻟﻄﺮﻓﯿﻦ ﺑﺮﻓﻊ٣
B)س–٢(٣×
) =٢٥(٣
آﺧﺮ ﺣﻞ:
B)س–٢(٢
) =٢٥(٣
س–٢=±)٢٥= (±)؟٢٥(٣
=±٥٣
Bس–٢=±)؟٢٥(٣
=±٥٣
Bس–٢=±١٢٥
Bس–٢=١٢٥س أو–٢=-١٢٥Bس–٢=١٢٥س أو–٢=-١٢٥
Bس=١٢٧س أو=-١٢٣Bس=١٢٧س أو=-١٢٣
Bم.ح=}١٢٧،-١٢٣{Bم.ح=}١٢٧،-١٢٣{
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٣[ــ س١٠س+٩=٠]٤[ــ س٣ــ س٤=٠
)س-٩) (س-١= (٠ﺑﺎﻟﺘﺤﻠﯿﻞ)س-٤) (س+١= (٠
Bس-٩=٠س ،-١=٠Bس=٤س=-١
Bس=٩Bس=١Bس٢
=٤٣
س٢
) =-١(٣
=-١
Bس٢
=٩٥
Bس٢
=١٥
=١Bس=±)؟٤(٣
س=±؟-١hح
Bس=±)؟٩(٥
Bس=±١Bس=±٢٣
=±٨
Bس=±٣٥
Bم.ح=}٨،-٨{
س=±٢٤٣
Bم.ح=}٢٤٣،-٢٤٣،١،-١{
٢
٣
٥٢
٣
٥
٣
٢
٣
٤
٥
٥
٢
٥
٥ ٢
٥
٥
٢
٥
٥
٢
٥
٥
٢
٥
٥
٢
٥
٥
٢
٥
٥
٢
٣
٥
٤
٣
٥٢
٣
٥
٢
٣
٥ ٢
٣
٥
٢
٣
٥](https://image.slidesharecdn.com/2017-160826233717/85/2017-80-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٨١
]٥) [س+١= (٣٢آﺧﺮ ﺣﻞ:
اﻟﺤﻞ:ــ ﻟﻠﻘﻮة اﻟﻄﺮﻓﯿﻦ ﺑﺮﻓﻊ٢ﻟﻠﻘﻮة اﻟﻄﺮﻓﯿﻦ ﺑﺮﻓﻊ٢
B)س+١(٥
=٣٢ﻟﻠﻘﻮة اﻟﺠﺬر ﺑﺄﺧﺬ٥B)س+١(ــ٥
=٣٢-١
Bس+١=٥
؟٣٢"=٢B)س+١(٥
=٣٢
Bس=٢–١=١Bس+١) =٢٥
= (٢
Bم.ح=}١{Bس=٢–١=١
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]١[اﺧﺘﺼﺮ:
]٢[اﻟﻌﻼﻗﺔ ﺗﻜﻮن ﻣﺘﻰن
؟ا×ن
؟بﻗﯿﻢ ﻟﺠﻤﯿﻊ ﺻﺤﯿﺤﺔااﻟﺤﻘﯿﻘﯿﺔ ب ،.
]٣[ﯾﺄﺗﻰ ﻣﺎ أﻛﻤـﻞ:
)أ) (٨(ﺗﺴﺎوى ﺻﻮرة اﺑﺴﻂ ﻓﻰ) ..........ب) (٦(ﺗﺴﺎوى ﺻﻮرة اﺑﺴﻂ ﻓﻰ.......
)ﺟـ( ) (ﺗﺴﺎوى ﺻﻮرة أﺑﺴﻂ ﻓﻰ) .....د(٣
ﰈ)ﱂ٣(ﱂ
-١
ﺗﺴﺎوى ﺻﻮرة أﺑﺴﻂ ﻓﻰ......
)ھـ) (٥٢
ــ٣٢
(ﺻﻮرة أﺑﺴﻂ ﻓﻰ.......
-١
٢
-٥
٢
١
٥
٥
اﻟﻜﺴﺮﯾﺔ اﻷﺳﺲ ﻋﻠﻰ ﺗﻤﺎرﯾﻦ
واﻟﻤﻌﺎدﻻت واﻟﺠﺬوراﻟﻨﻮﻧﯿﺔ
؟٨×٤ــ١
×٢ــ
٦–٢
×٣٢
٢
٣
٥
٢
٣
٥
١
٤
٥
٣
٢
٥
١٦
٦٢٥
-٣
٤١
٤
٥
١
٣
٥](https://image.slidesharecdn.com/2017-160826233717/85/2017-81-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٨٢
]٥[اﻟﺨﻄﺄ اﻛﺘﺸﻒ:
)أ(ــ٩) =-٩= (؟)-٩("
٢
=؟٨١=٩
)ب(س ﻛﺎن إذا٤
=٨١س ﻓﺈن=٤
؟٨١Bس=٣
]٦[ﻧﻖ اﻟﻌﻼﻗﺔ ﻣﻦ اﻟﺤﺠﻢ ﺑﺪﻻﻟﺔ ﯾﻌﻄﻰ ﻛﺮة ﻗﻄﺮ ﻧﺼﻒ طﻮل ﻛﺎن إذا( ) =اﻟﺰﯾﺎدة أوﺟﺪ
ﻣﻦ اﻟﺤﺠﻢ ﯾﺘﻐﯿﺮ ﻋﻨﺪﻣﺎ اﻟﻘﻄﺮ ﻧﺼﻒ طﻮل ﻓﻰπإﻟﻰ٣٦πﻣﻜﻌﺒﺔ وﺣﺪة.
]٧[
]٨[س ﻛﺎن إذا=٣ص=٢٧س ﻗﯿﻤﺔ ﻓﻤﺎ+ص
]٩[
٢
٢
٥
٣ح
٤π
١
٢
٥
٣٢
٣
٣
٢
٥
٢
٣
٥](https://image.slidesharecdn.com/2017-160826233717/85/2017-82-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٨٣
]١٠[
]١١[اﻟﺼﺤﯿﺤﺔ اﻻﺟﺎﺑﺔ اﺧﺘﺮ:
] ...... =ا،ا–١،سا،١[
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻷﺳﯿﺔ اﻟﺪاﻟﺔﺗﻄﺒﯿﻘﺎﺗﮭﺎ و:
ﺗﻌﺮﯾﻒ:د ﻛﺎﻧﺖ إذا:حCح+
د ﺣﯿﺚ)س= (اس
ﻟﻜﻞاgح+-}١{
،سحﻣﺠﺎﻟﮭﺎ ﯾﻜﻮن وﻟﮭﺬا=ح،اس
ح+
ﻣﺪاھﺎ ﯾﻜﻮن وﻟﮭﺬا=ح+
أﺳﺎﺳﮭﺎ أﺳﯿﺔ داﻟﺔ ﺗﺴﻤﻰ د ﻓﺈنا
ﻣﺜﻞ:د)س= (٣س
اﺳﺎﺳﮭﺎ٣س أﺳﮭﺎ ،
د ،)س( ) = (س+٢
س أﺳﮭﺎ ، اﺳﺎﺳﮭﺎ+٢
ﻣﺜﺎل:
اس+٢
+اس+١
+اس
اس+١
+اس
+اس-
١
١
٢
٥
١
٢
٥
أن ﺗﺬﻛﺮ:
]١[اﻟﺠﺒﺮﯾﺔ اﻟﺪاﻟﺔ:اﻟﻤﺴﺘﻘﻞ اﻟﻤﺘﻐﯿﺮ ﯾﻜﻮن)س(ﺣﻘﯿﻘﻰ ﻋﺪد اﻷس أﻣﺎ اﻷﺳﺎس ھﻮ
ﻣﺜﻞ:د)س= (س٢
د ،)س= (س٣
+، س٠٠٠٠
]٢[اﻷﺳﯿﺔ اﻟﺪاﻟﺔ:اﻟﻤﺴﺘﻘﻞ اﻟﻤﺘﻐﯿﺮ ﯾﻜﻮن)س(ﺣﻘﯿﻘﻰ ھﻮﻋﺪد اﻷﺳﺎس أﻣﺎ اﻷس ھﻮ
اﻟﻮاﺣﺪ ﯾﺴﺎوى ﻻ ﻣﻮﺟﺐ
ﻣﺜﻞ:د)س= (٢س
د ،)س= (٣س–١
،٠٠٠٠٠](https://image.slidesharecdn.com/2017-160826233717/85/2017-83-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٨٤
*اﻟ اﻟﺘﻤﺜﯿﻞاﻷﺳﯿﺔ ﻟﻠﺪاﻟﺔ ﺒﯿﺎﻧﻰ:
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﻟﺪاﻟﺔ ﻣﻨﺤﻨﻰ أرﺳﻢد)= (۲
اﻟﻔﺘﺮة ﻓﻲ]–٣،٤[ﻣﻦ وأوﺟﺪ اﻟﺮﺳﻢ:
)١(د)–٠.٥()۲(د)١.٥(
)٣(ﻟﻠﻌﺪد ﺗﻘﺮﯾﺒﯿﺔ ﻗﯿﻤﺔ]ﺢﺧ۲/٣/)٤(اﻟﻤﻌﺎدﻟﺔ ﺣﻞد)= (١٠
اﻟﺤﻞ:
د ﻗﯿﻤﺔ ﻹﯾﺠﺎد)–٠.٥: (
ﻋﻨﺪ ﻣﺴﺘﻘﯿﻤﺎ ﻧﺮﺳﻢً–٠.٥اﻟﺼﺎدات ﻣﺤﻮر ﯾﻮازى
ﺗﻘﺮﯾﺒﺎ ﺗﺴﺎوى ﻓﻨﺠﺪھﺎ ﻧﻘﻄﺔ ﻋﻨﺪ اﻟﻤﻨﺤﻨﻰ ﻟﯿﻘﺎﺑﻞً٠.٧
Bد)–٠.٥= (٠.٧
د ﻗﯿﻤﺔ ﻹﯾﺠﺎد)١.٥(ﺳﺒﻖ ﻛﻤﺎ ﻧﺮﺳﻢ
أن ﻧﺠﺪ:د)١.٥= (٨.۲
ﻗﯿﻤﺔ ﻹﯾﺠﺎد]ﺢﺧ۲/٣/أن ﻧﻼﺣﻆ:٣۲=۲
٥
Bد ﻧﻮﺟﺪ)%؛٢(=د)!؛٢۲(اﻟﺴﺎﺑﻖ ﻓﻰ ﻛﻤﺎ وﻧﺮﺳﻢ
Bﻗﯿﻤﺔ]ﺢﺧ۲/٣/=٥.٧
٤٣۲١٠–١–۲–٣
ص١٦٨٤۲١!؛٢!؛٤!؛٨](https://image.slidesharecdn.com/2017-160826233717/85/2017-84-320.jpg)


![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٩٠
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
*اﻷﺳﯿﺔ اﻟﻤﻌﺎدﻻت ﺣﻞ*
ھﺎﻣﺔ ﻗﻮاﻋﺪ:
١-ﻛﺎن إذا:ام
=ان
ﻓﺈن:م=نﺣﯿﺚ:اgﺣﺢ-c٠،١،-١d
ﻣﺜﻼ:ﻛﺎن إذا٣س+٤
=٣٣
ﻓﺈنس+٤=٣Bس=٣–٤=-١
٢-ﻛﺎن إذا:ام
=بم
ﻓﺈن:
*م=٠ﺣﯿﺚا}٠،ب}٠،ا}_ب
ﻣﺜﻼ:٧س-٤
=٥س-٤
ﻓﺈن:س–٤=٠Bس=٤
*ا=بﻛﺎن إذامﻋﺪد، ﻓﺮدﯾﺎ اا}٠،ب}٠
ﻣﺜﻼ:ﻛﺎن إذاس٣
=[ ]=٣
Bس=
*|ا|=|ب|ﻛﺎن إذام، زوﺟﯿﺎ ﻋﺪداا}٠،ب}٠
ﻣﺜﻼ:س٢
=[ ]=٢
Bس=_
١
٨
١
٢
١
٢
١
٤
١
٢
١
٢](https://image.slidesharecdn.com/2017-160826233717/85/2017-90-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٩١
ص ،$=٨١) =٣(٤
) =-٣(٤
Bص=_٣
٣-ﻛﺎن إذا:ام
=١ﻓﺈن:م=٠ﺣﯿﺚا}٠،ا}_١
ﻣﺜﻼ:ﻛﺎن إذا]ة٣[س-٢
=١Bس–٢=٠Bس=٢
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:
اﻟﺤﻞ:](https://image.slidesharecdn.com/2017-160826233717/85/2017-91-320.jpg)





![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٩٧
اﻟﻌﻜﺴﯿﺔ اﻟﺪاﻟﺔ ﺧﻮاص ﻣﻦ:
١(د أن ﯾﻘﺎل)س(ر ،)س(ﻟﻸﺧﺮى ﻋﻜﺴﯿﺔ داﻟﺔ
ﻛﺎن إذا)دºر) (س= (، س)رºد)(س= (س
٢(د اﻟﺪاﻟﺔ ﻣﺠﺎل)س= (د اﻟﻌﻜﺴﯿﺔ اﻟﺪاﻟﺔ ﻣﺪىـــ١
)س(
د اﻟﺪاﻟﺔ ﻣﺪى)س= (اﻟﺪا ﻣﺠﺎلد اﻟﻌﻜﺴﯿﺔ ﻟﺔــ١
)س(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د ﺣﯿﺚ د ﻟﻠﺪاﻟﺔ اﻟﻌﻜﺴﯿﺔ اﻟﺪاﻟﺔ أوﺟﺪ)س= (٢س+١ﺑﯿﺎﻧﯿﺎ ﻣﻌﻜﻮﺳﮭﺎ و اﻟﺪاﻟﺔ ﻣﺜﻞ و
واﺣﺪ ﺷﻜﻞ ﻓﻰ.
اﻟﺤﻞ:Aص=٢س+١Bس=٢ص+١B٢ص=س–١
Bص) =س–١(Bدــ١
)س) = (س–١(
أن ﯾﻼﺣﻆ و:
د اﻟﻌﻜﺴﯿﺔ اﻟﺪاﻟﺔ و د اﻟﺪاﻟﺔــ١
ﻣﻨﺤﻨﺎﻣﺘﻤﺎﺛﻼن ھﻤﺎ
ص ﻟﻠﻤﺴﺘﻘﯿﻢ ﺑﺎﻟﻨﺴﺒﺔ=س
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:د ﺑﺤﯿﺚ داﻟﺔ د ﻛﺎﻧﺖ إذا)س= (٣+؟س"–"١"ﻓﺄوﺟﺪ:
أ(د ﻣﺠﺎل)س(د ﻣﺪى و)س(ب(دــ١
)س(ﻣﺪاھﺎ و ﻣﺠﺎﻟﮭﺎ ﻋﯿﻦ و
ﺟـ(د ﻣﻦ ﻟﻜﻞ اﻟﺒﯿﺎﻧﻰ اﻟﺸﻜﻞ ارﺳﻢ اﻟﺮﺳﻮﻣﯿﺔ اﻟﺒﺮاﻣﺞ أﺣﺪ ﻣﺴﺘﺨﺪﻣﺎ)س(د ،ــ١
)س(
اﻟﺤﻞ) :أ(د)س(س ﻗﯿﻢ ﻟﺠﻤﯿﻊ ﻣﻌﺮﻓﺔ–١X٠س أىX١
Bد ﻣﺠﺎل)س] = (١،∞]
A؟س"–"١"X٠اﻟﺪاﻟﺔ ﻣﺠﺎل ﻓﻰ اﻟﻮاﻗﻌﺔ س ﻗﯿﻢ ﻟﺠﻤﯿﻊ
س-١٠١
د)س(-١١٣
دــ١
)س(-١-٠.٥٠
١
٢
١
٢
د ﻣﺠﺎلــ١
)س(
سد)س(
د ﻣﺪى)س(
د ﻣﺠﺎل)س(
د ﻣﺪىــ١
)س(](https://image.slidesharecdn.com/2017-160826233717/85/2017-97-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
٩٨
B٣+؟س"–"١"X٣Gد)س(X٣Bد ﻣﺪى)س] = (٣،∞]
)ب(Aص=٣+؟س"–"١"ص ، س اﻟﻤﺘﻐﯿﺮات ﺑﺎﺳﺘﺒﺪال
Bس=٣+؟ص"–"١"Bس–٣=؟ص"–"١"اﻟﻄﺮﻓﯿﻦ ﺑﺘﺮﺑﯿﻊ
B)س–٣(٢
=ص–١Bص) =س–٣(٢
+١
Bدــ١
)س) = (س–٣(٢
+١
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻟﻌﻜﺴﯿﺔ اﻟﺪاﻟﺔ ﻋﻠﻰ ﺗﻤﺎرﯾﻦ](https://image.slidesharecdn.com/2017-160826233717/85/2017-98-320.jpg)

![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٠٠
*ﺗﻤﺜﯿﻠﮭﺎ و اﻟﻠﻮﻏﺎرﯾﺘﻤﯿﺔ اﻟﺪاﻟﺔﺑﯿﺎﻧﯿﺎ:
ﺗﻌﺮﯾﻒ:ﻛﺎن إذا:اgح+–}١{،سgح،صgح+
ﻓﺈن:اﻟﻠﻮﻏﺎرﯾﺘﻤﯿﺔ اﻟﺪاﻟﺔص=ﻟـــــﻮاسﻟﻠﺪاﻟﺔ ﻋﻜﺴﯿﺔ داﻟﺔاﻷﺳﯿﺔص=ا
س
ﻣﺜﻼ:٨=٢٣
Eﻟـــــــﻮ٢٨=٣ﻟــﻮ ،٢٣٢=٥E٣٢=٢٥
،٢٤٣=٣٥
Eﻟـــــــﻮ٣٢٤٣=٥
ﻣﻼﺣﻈﺎت:
*ﻟـــــﻮاسﺗﻘﺮأﻟﻮﻏﺎرﯾﺘﻢسﻷﺳﺎسا
*اﻵﺳﯿﺔ ﻟﻠﺪاﻟﺔ اﻟﻌﻜﺴﯿﺔ اﻟﺪاﻟﺔ ھﻰ اﻟﻠﻮﻏﺎرﯾﺘﻤﯿﺔ اﻟﺪاﻟﺔ
*ﻓﻤﺜﻼ ﻣﻮﺟﺐ ﻏﯿﺮ ﻋﺪد ﻟﻮﻏﺎرﯾﺘﻢ ﻋﻦ ﻟﻠﺤﺪﯾﺚ ﻣﻌﻨﻰ ﻻ:ﻟﻮ٤–٣،ﻟﻮ۲
ﺻﻔﺮﻟﮫ ﻣﻌﻨﻰ ﻻ
*اﻷﺳﺎساﻋﺪد ﯾﻜﻮن أن ﯾﺠﺐﻣﻮ اًاﻟﺼﺤﯿﺢ اﻟﻮاﺣﺪ ﻋﻦ ﯾﺨﺘﻠﻒ ﺟﺒﺎً
ﻓﻤﺜﻼ:ﻟﻮ-۲
٨،ﻟﻮﺻﻔﺮ
٧ﻟﮫ ﻣﻌﻨﻰ ﻻ
*اﻟﻤﻌﺘﺎدة اﻟﻠﻮﻏﺎرﯾﺘﻤﺎت:
ا ھﻰأﺳﺎﺳﮭﺎ اﻟﺘﻰ ﻟﻠﻮﻏﺎرﯾﺘﻤﺎت=١٠ﯾﻜﺘﺐ وﻻ]اﻷﺳﺎس ھﺬا ﺣﺬف ﻋﻠﻰ أﺗﻔﻖ وﻗﺪ[
ﻓﻤﺜﻼ:ﻟﻮ٣ﺗﻌﻨﻰﻟﻮ١٠
٣
ﯾﻜﻮن ذﻟﻚ وﻋﻠﻰ:
ﻟﻮ١٠=١ﻟﻮ ،١٠٠=ﻟﻮ١٠
۲
=۲ﻟﻮ ،١٠٠٠=ﻟﻮ١٠٣
=٣وھﻜﺬا
ﻟﻮ ،٠.١=–١ﻟﻮ ،٠.٠١=–۲ﻟﻮ ،٠.٠٠١=-٣وھﻜﺬا
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻟﻰ اﻷﺳﯿﺔ اﻟﺪاﻟﺔ ﻣﻦ اﻟﺘﺤﻮﯾﻞاﻟﻌﻜﺲ اﻟﻠﻮﻏﺎرﯾﺘﻤﯿﺔ:اب
=جب ﻓﺈن=ﻟﻮاج
ﻣﺜﺎل:
اﻟﺤﻞ) :أ(A٢٧
=١٢٨Bﻟـﻮ٢١٢٨=٧
)ب(A)؟٢(١٠
=٣٢Bﻟــﻮ؟٢٣٢=١٠
)ﺟـ(A( )ــ٢
=Bﻟــﻮ=-٢ ٢
٣
٩
٤
٩
٤ ٢
٣](https://image.slidesharecdn.com/2017-160826233717/85/2017-100-320.jpg)
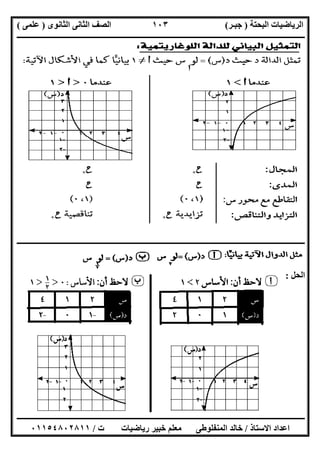

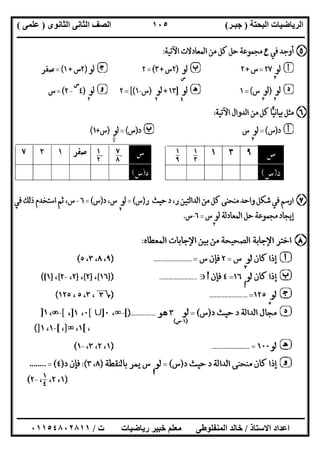


![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٠٨
ﻣﺜﺎل:ﻟـﻮ ﻗﯿﻤﺔ أوﺟﺪ٣١٥ﻟـﻮ ﻛﺎن إذا ﺻﻮرة أﺑﺴﻂ ﻓﻰ٣٥T١.٤٦٥
اﻟﺤﻞ:ﻟـﻮ٣١٥=ﻟـﻮ٣٥×٣=ﻟـﻮ٣٥+ﻟـﻮ٣٣=١.٤٦٥+١=٢.٤٦٥
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﺻﻮرة ﻻﺑﺴﻂ اﺧﺘﺼﺮ:٢ﻟﻮ٢٥+ﻟﻮ+ ( + )٢ﻟﻮ٣–ﻟﻮ٣٠
اﻟﺤﻞ:اﻟﻤﻘﺪار=ﻟﻮ)٢٥(٢
+ﻟﻮ+ﻟﻮ٣٢
ﻟﻮ ــ٣٠
=ﻟﻮ)٢٥(٢
× ×٩×=ﻟﻮ١٠٠
=٢ﻟﻮ١٠=٢
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:اﺧﺘﺼﺮ:ﻟﻮ٥٤٩×ﻟﻮ٨٥×ﻟﻮ٩٨×ﻟﻮ٧٩
اﻟﺤﻞ:اﻟﻤﻘﺪار=× × ×= = =٢
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:أن أﺛﺒﺖ=٣
اﻟﺤﻞ:اﻻﯾﻤﻦ=ﻟﻮ÷ﻟﻮ=ﻟﻮ( )٦
÷ﻟﻮ( )٢
=٦ﻟﻮ÷٢ﻟﻮ=٣=اﻻﯾﺴﺮ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ﻛﺎن إذا:٣س ﻟــﻮ+٤ص ﻟــﻮ–ﻟص س ــﻮ۲
=۲)ﻟــﻮ۲+ﻟـﻮ٣(
أن اﺛﺒﺖ:ص س=٦]ص س ﻗﯿﻤﺔ ﯾﻄﻠﺐ أﺧﺮ ﺳﺆال ﻓﻰ اﻟﻤﻌﻄﻰ ﺑﻨﻔﺲ[
اﻟﺤﻞ:
٣س ﻟــﻮ+٤ص ﻟــﻮ–ﻟـص س ـﻮ۲
=۲ﻟــﻮ۲+۲ﻟــﻮ٣
ﻟس ــﻮ٣
+ص ﻟــﻮ٤
–ﻟـص س ــﻮ۲
=ﻟـــﻮ)۲(۲
+ﻟــﻮ)٣(۲
ﻟـــــــ ــﻮـــــــــــــــــ=ﻟــــﻮ٤+ﻟـــــﻮ٩=ﻟـــﻮ٤×٩
ﻟـس ـــﻮ۲
ص۲
=ﻟـــﻮ٣٦Bس۲
ص۲
=٣٦Bص س=٦
١
٣
١
٥
٨
١٥
٨
١٥
١
٣٠
ﻟـﻮ٤٩
ﻟـﻮ٥
ﻟـﻮ٥
ﻟـﻮ٨
ﻟـﻮ٨
ﻟـﻮ٩
ﻟـﻮ٩
ﻟـﻮ٧
ﻟـﻮ٤٩
ﻟـﻮ٧
٢ﻟـﻮ٧
ﻟـﻮ٧
ﻟـﻮ٧٢٩ﻟﻮ ــ٦٤
ﻟـﻮ٩ﻟﻮ ــ٤
٧٢٩
٦٤
٩
٤
٣
٢
٣
٢
٣
٢
٣
٢
اﻷﯾﻤﻦ اﻟﻄﺮف ﻧﺠﻌﻞ
ﺑﮫ"ﻟــﻮ"
ﺑﺎﺳﺘﺨﺪام ﻓﻘﻂ واﺣﺪ
اﻟﻘﻮاﻧﯿﻦ
س٣
×ص٤
س×ص۲](https://image.slidesharecdn.com/2017-160826233717/85/2017-108-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١٠٩
ﻣﺜﺎل:س ﻛﺎن إذا٢
+ص٢
=٨أن أﺛﺒﺖ ص س٢ﻟﻮ)س+ص= (١+س ﻟﻮ+ص ﻟﻮ
اﻟﺤﻞ:Aس٢
+ص٢
=٨ﺑﺎﺿﺎﻓﺔ ص س٢ﻟﻠﻄﺮﻓﯿﻦ ص س
Bس٢
+٢ص س+ص٢
=٨ص س+٢ص س
B)س+ص(٢
=١٠اﻟﻄﺮﻓﯿﻦ ﻟﻮﻏﺎرﯾﺘﻢ ﺑﺄﺧﺬ ص س
Bﻟﻮ)س+ص(٢
=ﻟﻮ١٠ص س
B٢ﻟﻮ)س+ص= (ﻟﻮ١٠+س ﻟﻮ+ص ﻟﻮ=١+س ﻟﻮ+ص ﻟﻮ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:ص س ﻛﺎن إذا=٤؟٢اﻟﻤﻘﺪار ﻗﯿﻤﺔ أوﺟﺪ٥ﻟــﻮ٢س+٤ﻟــﻮ٢ص–ﻟــﻮ٢س٣
ص٢
اﻟﺤﻞ:
اﻟﻤﻘﺪار=ﻟــــــﻮ٢ـــــــــــــــــــــ=ﻟــــﻮ٢س٢
ص٢
=ﻟـــــﻮ٢)ص س(٢
=ﻟــــﻮ٢)٤؟٢(٢
=ﻟــــﻮ٢٣٢=ﻟــــﻮ٢٢٥
=٥ﻟــــﻮ٢٢=٥×١=٥
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:أن إﺛﺒﺖ:ﻟــــﻮ٢ﻟـــــﻮ٤ﻟــــــﻮ٨٦٤=-١
اﻟﺤﻞ:اﻟﻤﻘﺪار=ﻟـــــﻮ٢ﻟــــــﻮ٤ﻟـــــﻮ٨٨٢
=ﻟـــــﻮ٢ﻟــــــﻮ٤٢ﻟـــــﻮ٨٨
=ﻟــــﻮ٢ﻟــــــﻮ٤)٤(=ﻟــــﻮ٢ﻟـــﻮ٤٤
=ﻟــــــﻮ٢=ﻟــــﻮ٢٢-١
=-١ﻟـــﻮ٢٢=-١
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ﻣﺜﺎل:أن ﺗﺤﻘﻖ اﻟﺘﻰ س ﻗﯿﻤﺔ أوﺟﺪس ﻟــــﻮ=ــــــــــــــــــــــــــــ
اﻟﺤﻞ:
Aس ﻟــــﻮ=ــــــــــــــــــــــــــــــBس ﻟــــﻮ=ــــــــــــــــــــــــــــ
Bس ﻟــــﻮ=ــــــــــــــــــــــــــــــBس ﻟــــﻮ=ﻟــــﻮ٥Bس=٥
س٣
×ص٢
س٥
×ص٤
١
٢١
٢
١
٢
)ﻟﻮ٥(٢
–ﻟﻮ١٢٥
ﻟﻮ٠.٠٠٥
)ﻟﻮ٥(٢
–ﻟﻮ٥٣
ﻟﻮ٥–ﻟﻮ١٠٠٠
)ﻟﻮ٥(٢
–٣ﻟﻮ٥
ﻟﻮ٥–٣
ﻟﻮ٥–٣
ﻟﻮ٥]ﻟﻮ٥–٣[](https://image.slidesharecdn.com/2017-160826233717/85/2017-109-320.jpg)




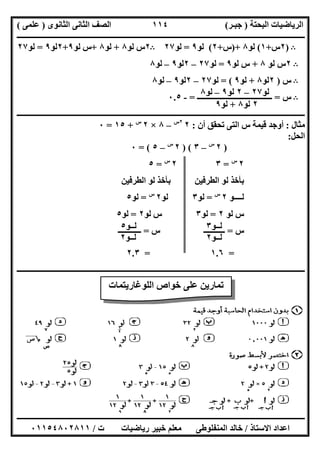
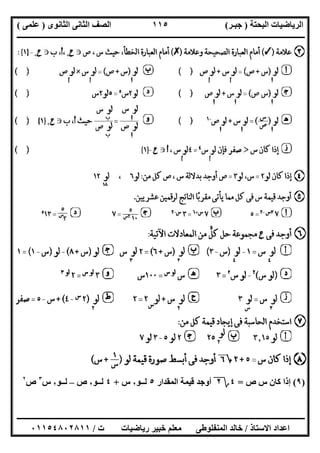
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١١٦
اﻟﻠﻮﻏﺎرﯾﺘﻤﺎت ﻋﻠﻰ ﻣﺘﻨﻮﻋﺔ ﺗﻤﺎرﯾﻦ:
]١[ﻣﻦ ﻛﻞ ﻗﯿﻤــﺔ أوﺟﺪ:ــ
١(ﻟﻮ٥٤٠–ﻟﻮ٥١٦+ﻟﻮ٥١٠
٢(ﻟﻮ٤۲+ﻟﻮ٤٥٦–ﻟﻮ٤٤۲+ﻟﻮ٤۲٤
٣(٣ﻟـﻮ-٢ﻟـﻮ-٤ﻟـﻮ-ﻟـﻮ٧٣
٤(ﻟــــﻮ٢ﻟـــــﻮ٤ﻟــــــﻮ٥٢٥
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٢[أن إﺛﺒــﺖ:ــ
١(ﻟـﻮ٢-ﻟـﻮ٢+ﻟـﻮ=ﻟـﻮ٣٢٧
٢(ﻟـﻮ٠.٧٥+ﻟـﻮ١۲–۲ﻟـﻮ٠.٣=ﻟـﻮ٦٣٦
٣= (٢
٤(س=ﻛﺎن إذا٧ﻟـﻮس+٤ﻟـﻮص–ﻟـﻮس٥
ص٢
=٢)ﻟـﻮ٢+ﻟـﻮ٣(
٥(ﻟـﻮس۲
=ﻟﻮصسأن إﺛﺒﺖ ﺛﻢ:ﻟﻮصس
٣
+ﻟﻮص۲س
٦
=٦ﻟﻮصس
ص
٢
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٣[ﯾﻠﻰ ﻓﯿﻤﺎ س ﻗﯿﻤــﺔ أوﺟﺪ:
١(ﻟـﻮس+ﻟـﻮ٤.٩=ﻟـﻮ٣٥–ﻟـﻮ١۲٥+ﻟـﻮ١٧٥
٢(ﻟـﻮ٢س=ﻟـﻮ+ﻟـﻮ١٢-٢ﻟـﻮ٠.٣
٣(ﻟـﻮ)س–١+ (ﻟـﻮ)س+١= (ﻟﻮ٨
٤(ﻟـﻮ)س۲
+٩س= (١
١
٢
٥
٣
٥
٧
١
٣
٧
١٢
٤٠
١٣
٩١
٦٠
١+ﻟﻮ۲–ﻟﻮ٤٥
١–ﻟﻮ١٥
٦
ص
٣
٤](https://image.slidesharecdn.com/2017-160826233717/85/2017-116-320.jpg)
![اﻟﺒﺤﺘﺔ اﻟﺮﯾﺎﺿﯿﺎت)ﺟﺒـﺮ(اﻟﺜﺎﻧﻮى اﻟﺜﺎﻧﻰ اﻟﺼﻒ)ﻋﻠﻤﻰ(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
اﻻﺳﺘﺎذ اﻋﺪاد/ت رﯾﺎﺿﯿﺎت ﺧﺒﯿﺮ ﻣﻌﻠﻢ اﻟﻤﻨﻔﻠﻮطﻰ ﺧﺎﻟﺪ/٠١١٥٤٨٠٢٨١١
١١٧
]٤[اﻟﻤ ﺣﻞ ﻣﺠﻤـﻮﻋﺔ أوﺟـﺪﻌاﻵﺗﯿﺔ ﺎدﻻت:
١(ﻟـــﻮ٢س+ﻟـــــﻮ٢)س-٢= (٣٢()ﻟـﻮ۲س(۲
+۲ﻟـﻮ۲س=٨
٣()س ﻟــــﻮ(٣
=س ﻟـــــﻮ٤
٤(ﻟﻮ۲س+ــــــــــــــ=٤
٥(ﻟـﻮ٣|س+١|=٢٦(٢×٦٤=٣٢
٧(٥٢س–٣
=٣س+٤
٨(٢٢س
–٨×٢س
+١٥=٠
٩(س=ﻟﻮ٣)ظﺎ(١٠(ﻟـﻮ٣ﻟـﻮ٢)س٢
–١٧= (١
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٥[ﯾﺄﺗﻰ ﻣﻤﺎ ﻛﻞ ﻓﻰ ﻋﺸﺮﯾﯿﻦ رﻗﻤﯿﻦ ﻷﻗﺮب س ﻗﯿﻤﺔ أوﺟﺪ:
١(ﻛﺎن إذا٥س
=١٧٢(ﻛﺎن إذا)١٨(٣س–٥
=٧.١٢
٣(ﻛﺎن إذا٨س+١
=٩س–٢
٤(٥
س–١
) =٦
س
÷٣٦(
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٦[ﻟﺮﻗﻢ اﻟﻨﺎﺗﺞ ﻣﻘﺮﺑﺎ س ﻗﯿﻢ أوﺟﺪ اﻟﺠﯿﺐ ﺣﺎﺳﺒﺔ ﺑﺈﺳﺘﺨﺪامﻋﺸﺮى:
١(۲
۲س
–١٠×۲
س
+۲٤=٠
٢(٣×٥
۲س+١
=۲٥×٩
س+١
٣(س=٢ﻟــــﻮ٧–٣ﻟـــــﻮ٢
٤(د ﻛﺎن إذا)س= (٣
س
،د)س+ (د)س–٢= (٢٠٠
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٧[اﻟﻜﺮة ﺣﺠﻢ ﻛﺎن إذا=$؛٣طﻧﻖ
٣
ﺣﺠﻤﮭﺎ اﻟﺘﻰ اﻟﻜﺮة ﻗﻄﺮ ﻧﺼﻒ طﻮل أوﺟﺪ=٩٠٤.٣۲ﺳﻢ٣
ط ﻣﺘﺨﺬا=٣.١٤ﺳﻢ ﻟﻘﺮب
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
]٨[ــــــــــــ ﻛﺎن إذا=ــــــــــــــ=ــــــــص ، س ﻗﯿﻤﺘﻰ أوﺟﺪ ــــــ
٣
ﻟﻮ۲س
)ﻟــﻮس(٢
)ﻟــﻮس(
ط
٣
س ﻟـــﻮ
ﻟـــﻮ٥
ﻟـــﻮ٩
ﻟـــﻮ٣
ﻟـــﻮ٤٩
ﻟــــﻮص](https://image.slidesharecdn.com/2017-160826233717/85/2017-117-320.jpg)