المستند يتضمن مجموعة متنوعة من تمارين الرياضيات للصف الثالث متوسط، حيث يطرح أسئلة متعددة حول حل المعادلات. تحتوي الوثيقة على خطوات الحلول لبعض المعادلات الرياضية، بالإضافة إلى توضيح المفاهيم الهندسية المتعلقة بالمسائل المطروحة. تعتبر هذه التمارين مفيدة لتعزيز الفهم الرياضي لدى الطلاب.
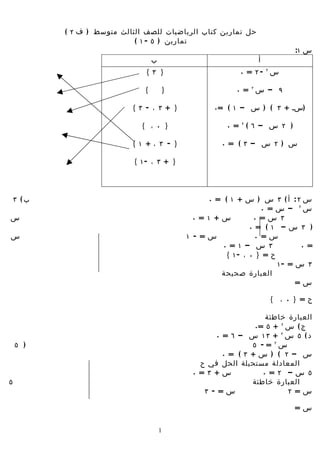





![س ٤: س ٣ : العدد الول = س
الول = س العدد الثاني = س + ٢
الثاني = س + ١ ناتج ضربهما = س ) س + ٢ ( =
٢
مربع الول = س س٢ + ٢ س
٢
مربع الثاني = ) س + ١ ( = س
٢
مجموعهما = س + ) س + ٢ ( = ٢
+ ٢ س+ ١ س+ ٢
س ٢ – ) س + ٢ س + ١ ( = ٥١
٢
ثلثة أمثال مجموعهما = ٣ ) ٢ س
س ٢ – س ٢ - ٢ س - ١ = ٥١ + ٢ ( = ٦ س+ ٦
- ٢ س – ١ = ٥١ ٦ س+ ٦ – ) س + ٢ س (= ٦
٢
٢ س + ١ = - ٥١ ٦ س + ٦ - س٢ - ٢ س = ٦
٢ س = - ٥١ - ١ - س٢ + ٤ س = ٦ – ٦
٢ س = - ٦١ س٢ – ٤ س = ٠
س= - ٨ س ) س – ٤ ( = ٠
الول = - ٨ س س= ٠
الثاني = - ٨ + ١ = - ٧ - ٤ = ٠
س س= ٣
س ٦ : الطول = ط س٤٥ : العدد = س =
العرض = ع معكوسه الضربي =مقبول
٢ × ) ط + ع ( = ٦٧ مقبول أمثال معكوسه الضربي =
ثمانية
ط + ع = ٦٧ ÷ ٢ = ٨٣ الول س+==
الول ٢ ٠
ع = ٨٣ - ط س٢ + ٢ س = ٨
ط × ع = ٠٦٣ س٢ + ٢ س – ٨ = ٠
ط ) ٨٣ – ط ( = ٠٦٣ ) س – ٢ ( ) س+ ٤ ( = ٠
٨٣ ط – ط ٢ = ٠٦٣ س - ٢ = ٠
ط ٢ – ٨٣ ط + ٠٦٣ = ٠ س+ ٤ = ٠
) ط – ٨١ ( ) ط – ٠٢ ( = ٠ س= ٢
ط - ٨١ = ٠ س= - ٤
ط - ٠٢ = ٠ مقبول
ط = ٨١ مرفوض
ط = ٠٢ العدد = ٢
مرفوض
س ٨ : ] م ن [ محصورة بين منتصفي
مقبول
ضلعي المثلث أ ب جس
س ٧ : القاعدة = ق
أي أن │ = ٠٢│ = │ ب جس│
طم ن
│ ب جس│ = ٨٣ –م ٠٢ = ٨١ الرتفاع = ع
ع= ٢ │ ن │
ق= ٢ ع
= ٢ × ٢ س٢ + ٦ س
= ١٢١
= ٤ س٢ + ٦ س
= ١٢١
+ ٣٢ = ٤ + ٣٢ س٢ + ٦ س
ع ٢ = ١٢١
= ٣١ ٢
) س+ ٣ (
ع = ± ١١
س+ ٣ =±
ع = ١١
س= - - س= - ٣
ق = ٢ × ١١ = ٢٢
٣
مقبول
مرفوض
س =7 - ٣](https://image.slidesharecdn.com/32-110306145016-phpapp02/85/3-2-7-320.jpg)



![│ ب جس│ ٢ = │ أ ب│ ٢+│ أ جس│
٢
٢
│ ب جس│ ٢ = ٦١ ٢ + ٠١
│ ب جس│ ٢ = ٦٥٢ + ٠٠١
│ ب جس│ ٢ = ٦٥٣
بأخذ الجذر التربيعي للطرفين
│ ب جس│ ≈ ٩.٨١
بعد الشخص عن نقطة النطلق ≈ ٩.٨١ م
^ المثلث أ ب جس قائم الزاوية ٥
أ ب جس = ٠٩ س ٤: زوايا المربع قوائم
^
في ب
│ أ جس│ = │ أ ب│ +│ ب جس│
٢ ٢ ٢
د
أ ٢
│ أ جس│ ٢ = ٥ ٢ + ٥
│ أ جس│ ٢ = ٥٢ + ٥٢
│ أ جس│ ٢ = ٠٥
بأخذ الجذر التربيعي للطرفين
5 │ أ جس│ = = ٥
جـ ب
س ٥ : نفرض أن طول ضلع المربع = س
٥ ٢
│ أ جس│ ٢ = │ أ ب│ ٢+│ ب جس│
د أ ٢
٠١٢ = س ٢ + س
٢
٠٠١ = ٢ س
س ٢ = ٠٥
01 بأخذ الجذر التربيعي للطرفين
س س = = ٥
^
س ٦ : نرسم م ن عمودي على الوتر ] أ ب [ فنحصل على المثلث أأ ن م القائم الزاوية في
4 جـ ب ن
س
4 ب ن
وحيث أن الفطر العمودي على وتر في دائرة يمر في منتصف ذلك الوتر فإن │ أ ن│=
5
×م ٤ سم
٢
│ م ن│ = │ أ م│ - │ أ ن│
٢ ٢
٢
│ م ن│ ٢ = ٥ ٢ - ٤
│ م ن│ ٢ = ٥٢ - ٦١
│ م ن│ ٢ = ٩
بأخذ الجذر التربيعي للطرفين
│ م ن│ = ٣
أي أن مركز الدائرة يبعد عن الوتر مسافة ٣ سم ٠
س ٧: المثلث أ ن م قائم الزاوية في ن
^
ب ٣ ن ٣ أ ٢
│ أ م│ ٢ = │ أ ن│ ٢+│ م ن│
٤
٢
│ أ م│ ٢ = ٣ ٢ + ٤
٤ │ أ م│ ٢ = ٩ + ٦١
×م
│ أ م│ ٢ = ٥٢
بأخذ الجذر التربيعي للطرفين
11](https://image.slidesharecdn.com/32-110306145016-phpapp02/85/3-2-11-320.jpg)






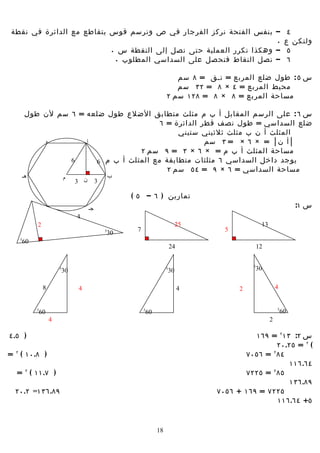
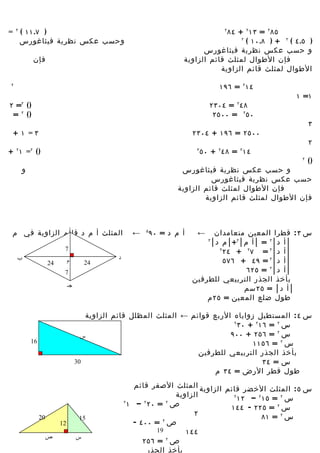
![بأخذ الجذر التربيعي للطرفين
س= ٩
س ٦ : ^أ = ٠٩ ٥ ← المثلث أ ب جس قائم الزاوية في أ
ب
٢
│ أ جس│ ٢ = │ ب جس│ ٢- │ أ ب│
٢
│ أ جس│ ٢ = ٣١ ٢ - ٥
│ أ جس│ ٢ = ٩٦١ - ٥٢
31
5 │ أ جس│ ٢ = ٤٤١
بأخذ الجذر التربيعي للطرفين
أ جـ │ أ جس│ = ٢١
د
بما أن د منتصف ] أ جس [
│ أ د│ = = ٦ سم
تابع س ٦:
^أ = ٠٩ ← المثلث أ ب د قائم الزاوية في أ٥
٢
│ ب د│ ٢ = │ أ ب│ ٢+│ أ د│
٢
│ ب د│ ٢ = ٥ ٢ + ٦
│ ب د│ ٢ = ٥٢ + ٦٣
│ ب د│ ٢ = ١٦
بأخذ الجذر التربيعي للطرفين
│ ب د│ =
المثلث الخضر قائمس ٧: المثلث الصفر قائم الزاوية
5 4 الزاوية ٢
س ٢ = ٦٢ – ٤
٢
ص ٢ =) ٢ ( ٢ + ٥ س ٢ = ٦٣ - ٦١
س ص ٢ = ٠٢ + ٥٢ س ٢ = ٠٢
ص 6
ص ٢ = ٥٤ بأخذ الجذر التربيعي للطرفين
بأخذ الجذر التربيعي س= ٢
للطرفين
ص= ٣
س ٨ : أ ( طول نصف قطر الدائرة = ٨ ÷ ٢ = ٤
طول ضلع المثلث = نسق = ٤ × = ٢١ سم
طول ضلع السداسي = نسق = ٤
طول ضلع المربع = نسق = ٤ × = ٤ سم
س ٩: من الرسم المقابل : المثلث قائم الزاوية
س
٢
س ٢ = ٨٢ + ٤
8
س ٢ = ٤٦ + ٦١
س ٢ = ٠٨
4 بأخذ الجذر التربيعي للطرفين
س = ٤ ≈ ٩.٨ م
21 21 طول الحبل ≈ ٩.٨ م
02
4](https://image.slidesharecdn.com/32-110306145016-phpapp02/85/3-2-20-320.jpg)


