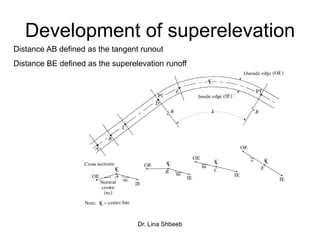
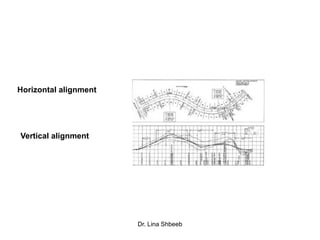
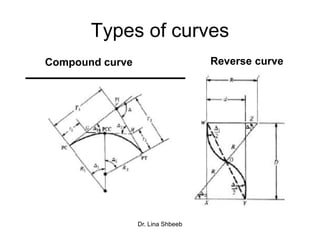
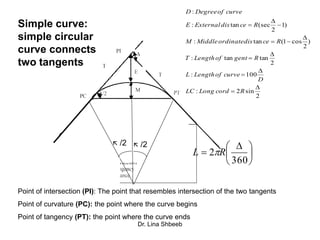
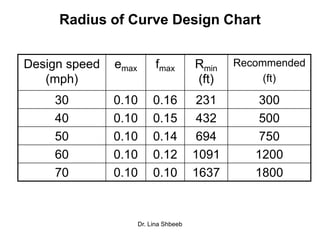
The document discusses horizontal alignment in transportation engineering. It defines horizontal alignment as straight segments connected by circular curves. It describes different types of curves like simple, compound, and reverse curves. It provides formulas to calculate curve length, radius, degree of curve, and sight distance. Examples are given to demonstrate calculating curve length, radius, and minimum sight distance around a curve. Methods for attaining superelevation on curves through pavement revolutions are also summarized.

1. Dr. Lina Shbeeb
Horizontal alignment
Transportation Engineering

2. Dr. Lina Shbeeb
Geometric design
• Consists of the following:
• Horizontal Design of roadways (Horizontal
design)
• Vertical Design of roadways (Vertical design)
• Cross-sectional Design (pavement design, no of
lane, etc)
• Terminal Facilities (Parking Lots, Garages, etc)
• Intersections & Interchanges.

3. Dr. Lina Shbeeb
Horizontal alignment
Vertical alignment

4. Dr. Lina Shbeeb
Horizontal Alignment (HA)
• Definition: Straight segments of roadways
(tangents) connected by suitable curves
(horizontal curves) there might be a need to
provide transitions.
• Curves require superelevation to provide
banking of curve, retard sliding, allow more
uniform speed.
• The length of the facility is measured along the
horizontal of control line like the center line and
is usually expressed in terms of 100-ft stations
from a reference point (i.e. sta 14 is located at
1400 ft from a reference point.

5. Dr. Lina Shbeeb
Types of curves in horizontal
alignment
• simple curves: it will be discussed in the
following section.
• Compound Curves consist of 2 or more curves
in succession turning in the same direction with
a common tangent point
• Reverse Curves consist of two simple curves
with equal radii turning opposite directions with a
common tangent
• Transition or Spiral curves are placed between
tangents and circular curves or between two
adjacent circular curves with substantially
different radii.

6. Dr. Lina Shbeeb
Types of curves
Compound curve Reverse curve

7. Dr. Lina Shbeeb
2
sin2:
100:
2
tantan:
)
2
cos1(tan:
)1
2
(sectan:
:











RcordLongLC
D
curveofLengthL
RgentofLengthT
RcedisordinateMiddleM
RcedisExternalE
curveofDegreeD
2
cos
1
2
sec



 /2  /2
Simple curve:
simple circular
curve connects
two tangents
Point of intersection (PI): The point that resembles intersection of the two tangents
Point of curvature (PC): the point where the curve begins
Point of tangency (PT): the point where the curve ends





 

360
2 RL 

8. Dr. Lina Shbeeb
Radius Calculation
Rmin = ___V2______
15(e + fs)
Where:
V = velocity (mph)
e = superelevation
fs =side friction coefficient
15 = gravity and unit
conversion
fs is a function of
• speed,
• Roadway surface,
• weather condition,
• tire condition, ect
• AASHTO: 0.5 if the
speed is 20 mph with
new tires and wet
pavement to 0.35 if
speed becomes 60
mph
e-value as function of road
and surface conditions
0.1: commonly used,
highway
0.08: snow and ice,
highway
0.12: low-volume, gravel-
surfaced, rural (drainage)
0.4-0.6: urban, traffic
congestion

9. Dr. Lina Shbeeb
Degree of curve
• As two tangents intersect they can be connected with infinite
number of curves that differ by D: Degree of curve they
have two definitions one for highway and one for railway
– The arc definition (highway) is equal to the central angle in degree
subtended by an arc of 100 ft; the relation between D and R is
estimated by
– The Chord definition (Railway) is equal to the central angle in degree
subtended by a cord of 100 ft; the relation between D and R is
estimated by








R
D
D
R
58.5729
3602
100

R
D 50
2
sin 






10. Dr. Lina Shbeeb
Degree of curve
100ft
Arc Definition Chord Definition

11. Dr. Lina Shbeeb
Radius of Curve Design Chart
Design speed
(mph)
emax fmax Rmin
(ft)
Recommended
(ft)
30 0.10 0.16 231 300
40 0.10 0.15 432 500
50 0.10 0.14 694 750
60 0.10 0.12 1091 1200
70 0.10 0.10 1637 1800

12. Dr. Lina Shbeeb
Radius Calculation (Example)
Design radius example: assume a maximum e
of 8% and design speed of 60 mph, what is
the minimum radius?
fmax = 0.12 (from ASSHTO for speed 60)
Rmin = 602/ 15(0.08 + 0.12)=1200 ft

13. Dr. Lina Shbeeb
Horizontal Curve Example
• Deflection angle of a 5º curve is 55º30’, PC at
station 238 + 44.75. Find length of curve,T, and
station of PC.
• D = 4º
•  = 55º30’ = 55.5º
• D = 5729.58 R = 5729.58 = 1,145.9 ft
R 5

14. Dr. Lina Shbeeb
Horizontal Curve Example
• D = 5º
•  = 55.5º
• R = 1,145.9 ft
• L = 2R = 2(1,145.9 ft)(55.5º) = 1109.4ft
360 360

15. Dr. Lina Shbeeb
Horizontal Curve Example
• D = 4º
•  = 55.417º
• R = 1,145.9 ft
• L = 1109.4 ft
• T = R tan  = 1,145.9 ft tan (55.5) = 583.97 ft
2 2

16. Dr. Lina Shbeeb
Sight Distance for Horizontal
Curves
• Location of object along
chord length that blocks
line of sight around the
curve
• m = R(1 – cos [28.65 S])
R
Where:
m = line of sight
S = stopping sight distance
R = radius

17. Dr. Lina Shbeeb
Sight Distance Example
A horizontal curve with R = 800 ft is part of a 2-
lane highway with a posted speed limit of 35
mph. What is the minimum distance that a
large billboard can be placed from the
centerline of the inside lane of the curve without
reducing required SSD? Assume p/r =2.5 and
a = 11.2 ft/sec2
SSD = 1.47vt + _________v2____
30(__a___  G)
32.2

18. Dr. Lina Shbeeb
Sight Distance Example
SSD = 1.47(35 mph)(2.5 sec) +
_____(35 mph)2____ = 246 feet
30(__11.2___  0)
32.2

19. Dr. Lina Shbeeb
Sight Distance Example
m = R(1 – cos [28.65 S])
R
m = 800 (1 – cos [28.65 {246}]) = 9.43 feet
800

20. Dr. Lina Shbeeb
Development of superelevation
Distance AB defined as the tangent runout
Distance BE defined as the superelevation runoff

21. Dr. Lina Shbeeb
Methods of Attaining Superelevation
1. Pavement revolved about center line
Centerline is point of control
2. Pavement revolved around inner edge
Inner edge is point of control
3. Pavement revolved around outer edge
Outer edge is point of control