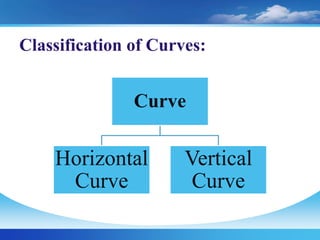
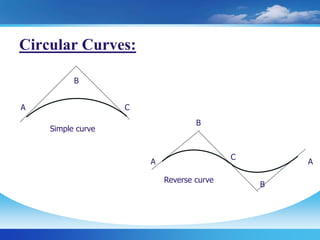
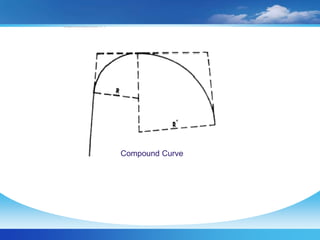
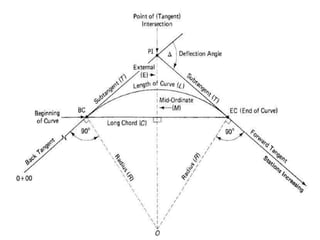
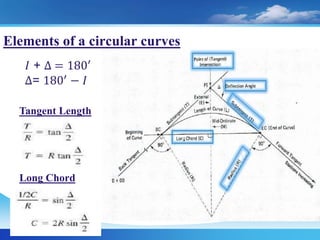
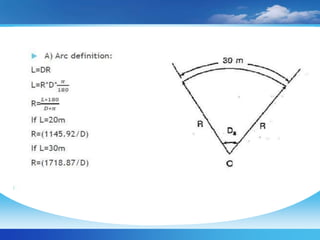
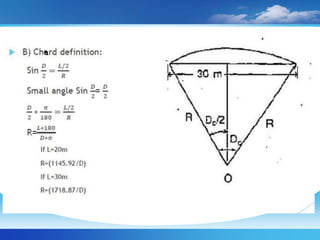
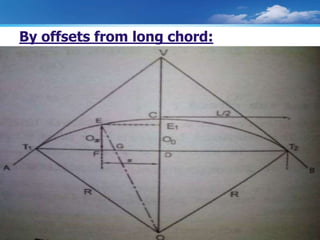
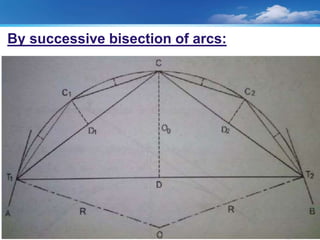
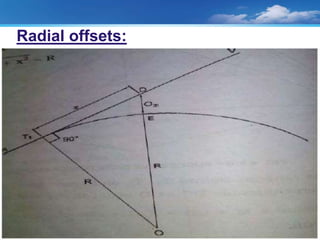
The document discusses setting out curves for highways. It defines different types of curves, including horizontal and vertical curves. Horizontal curves can be circular, transition, or lemniscate curves. Vertical curves connect different gradients and can be circular arcs or parabolic arcs. Common elements of circular curves are defined, such as tangents, points of intersection, and long chords. Methods for setting out simple circular curves include linear methods using offsets from long chords, bisection of arcs, tangents, or chords produced.

1. CE2307: Advanced Engineering
Surveying
Engr. Muhammad Irfan
irfan7235@yahoo.com
Department of Civil Engineering
The University of Lahore (Islamabad
Campus)

2. Overview of Course
CE2307: Advanced Engineering Surveying
Office: 4rth floor, 2nd room from right
Email: irfan7235@yahoo.com
Reference books:
1. Surveying and leveling by T.P Kanetkar and S.V
Kulkarni.
2. Surveying with construction applications, 7th edition,
Pearson Education by Kavanagh Barry.
3. Surveying and leveling 2nd edition N.N Basak.
4. Engineering surveying 6th edition by W. Schofield and
M. Breach.

3. Lecture 2
CURVES AND SETTING OUT OF
HIGHWAY CURVES

4. CURVES
a. Curves are usually employed in the line of
communication in order that the change of
direction at the intersection of the straight lines be
gradual.
b. Generally circular arcs but they can be parabolic
as well.
ROAD ALIGNMENT

5. CURVES
They enable the vehicle to pass
from one path on to another
when the two paths meet at an
angle. They are also used in the
vertical plane at all changes of
grade to avoid the abrupt change
of grade at the apex.

6. NEED OF PROVIDING CURVES
Curves are needed on Highways, railways and
canals for bringing about gradual change of
direction of motion. They are provided for following
reasons:-
i) To bring about gradual change in direction of
motion.
ii) To bring about gradual change in grade and for
good visibility.

7. iii) To alert the driver so that he may
not fall asleep.
iv) To layout Canal alignment.
v) To control erosion of canal banks by
the thrust of flowing water in a canal.

8. Curve
Horizontal
Curve
Vertical
Curve
Classification of Curves:

9. Horizontal Curve Vertical Curve

10. ROAD ALIGNMENT
Horizontal Curve

11. ROAD ALIGNMENT
Vertical Curve

12. CLASSIFICATION OF HORIZONTAL CURVES:
Horizontal curves are provided in horizontal plane.
Its types include circular curves ,transition curves
and lemniscate curves.
Circular Curves:
a. Simple Curve
b. Reverse Curve
c. Compound Curve

13. Circular Curves:
Simple curve
A
B
C
Reverse curve
A
B
C
B
A

14. Compound Curve

15. TRANSITION CURVES:
Curve of varying radius called a transition curve between the
tangent and a circular curve. The transition curve is also called the
spiral or easement curve

16. VERTICAL CURVE:
When two different gradients meet, they are
connected by a curve in a vertical plane called a
vertical curve. The vertical curve may be circular arc
or an arc of a parabola.
Types of Vertical Curves:
a. An up grade followed by a down grade.
o
A
B
C
ROAD ALIGNMENT
Vertical curve

17. b. A down grade followed by an up grade.
c. An up grade followed by another up grade.
A
B
E
F
ROAD ALIGNMENT
A
B

18. d. A down grade followed by another down grade.
ROAD ALIGNMENT

19. Parts of Circular Curve:
-The straight line T1 B and T2 B, which are connected by the curve are called
the tangents or straights to the curve.
-The Point B at which the two tangent lines T1B and T2B intersect is known
as the point of intersection (P.I)
-The tangent line T1Bis called the first tangent or back tangent.
-The tangent line BT2 is called the second tangent or forward tangent
ROAD ALIGNMENT

20. -The point T1 and T2 at which the curve touches the straight are called
tangent points.
-The angle T1BT2 between two tangent lines is called the angle of Intersection (I).
-The line T1T2 joining the two tangent points is known as the long chord (L).
-The arc T1FT2 is called the length of the curve.
-Ø is called the Deflection Angle
-The mid point(F) of the arc (T1FT2) is called the summit or apex of the curve
-The distance from the point of intersection to the apex of the curve BF is
called the apex distance
F
E

21. The distance between the apex of the curve and the mid point of the long chord
(EF) is called versed sine of the curve.
The angle subtended at the center of the curve by the arc T1FT2 is known as
central angle and is equal to the deflection angle (φ).
The distance from the point of intersection to the tangent point is called
tangent length (BT1 and BT2).

23. Super-elevation
-When a particle moves in a circle, a force known as
centrifugal force act upon it and tends to push it away from
circle.
-Similar force is experienced by a vehicle on circular path.
-Only weight of vehicle can resist this force which is
insufficient.
-To counter-balance this force, the outer edge of the road is
raised to some height (w.r.t inner edge)
-The height through which the outer edge is raised is called
Super-elevation.

24. Super-elevation
Formula derivation
For Roads
For Railway
When θ becomes
small then
sinθ=tanθ=h/b

25. Centrifugal Ratio
The ratio between centrifugal force and
weight of vehicle is called C.R.
(Used when V is in m/sec)

26. Example:
Radius of circular road= 300 m
Width of road= 8 m
Speed of vehicle= 50 km/hr
Take CR= 1/10
Calculate super elevation value.

27. Elements of a circular curves
Tangent Length
Long Chord

28. 180180
πRφπφR.Rφl 






Length of curve
Apex distance

29. Versed sine of curve
Chainage at BC= Chainage at PI – T
Chainage at EC= Chainage at BC + length of curve

30. 

31. Designation of a curve:
-A curve may be designated either by the radius or
by the angle subtended at the center by an arc of
specified length.

34. Relation between the Radius of curve and Degree of Curve:
The relation between the radius
and the degree of the curve may
be determined as follows:-
Let R = the radius of the curve in m.
D = the degree of the curve.
MN = the chord, 30m long.
P = the mid-point of the chord.
In OMP,OM=R,
MP= ½ MN =15m
MOP=D/2

35. Then, sin D/2=MP/OM= 15/R
Or R = 15/(sin D/2)--------(Exact)
But when D is small, sin D/2 may be
assumed approximately equal to
D/2 in radians.
Therefore:
R = 15X2x180/3.14xD
= 1718.87/D
Or say , R = 1719/D-------(Approximate)
Note: This relation holds good up to 5 degree
Curves. For higher degree curves the
exact relation should be used.

36. Exercise:
Perform same steps considering length of
chord to be 10m, 20m and 100 ft and
compare all the results.

37. Methods of setting out simple circular curve:
Based on the instruments used in setting
out the curves on the ground there are two
methods:
1) Linear method
2) Angular method

38. Linear Method:
In these methods only tape or chain is used
for setting out the curve . Angle measuring
instruments are not used.
Main linear methods are:
By offsets from the long chord.
By successive bisection of arcs.
By offsets from the tangents.
By offsets from chord produced

39. By offsets from long chord:

41. By successive bisection of arcs:

42. 

43. By offsets from the tangents:
The offsets from the tangents can be of two types:
Radial offsets
If the center of curve O is accessible from the
points on tangent, this method of curve setting is
possible.
Perpendicular offsets
If the center of a circle is not visible, perpendicular
offsets from tangent can be set to locate the
points on the curve.

44. Radial offsets:

46. Perpendicular offsets:

48. /2

52. Offsets from chords produced:
C3
C3
C2
C1
E
D

53. 

55. R