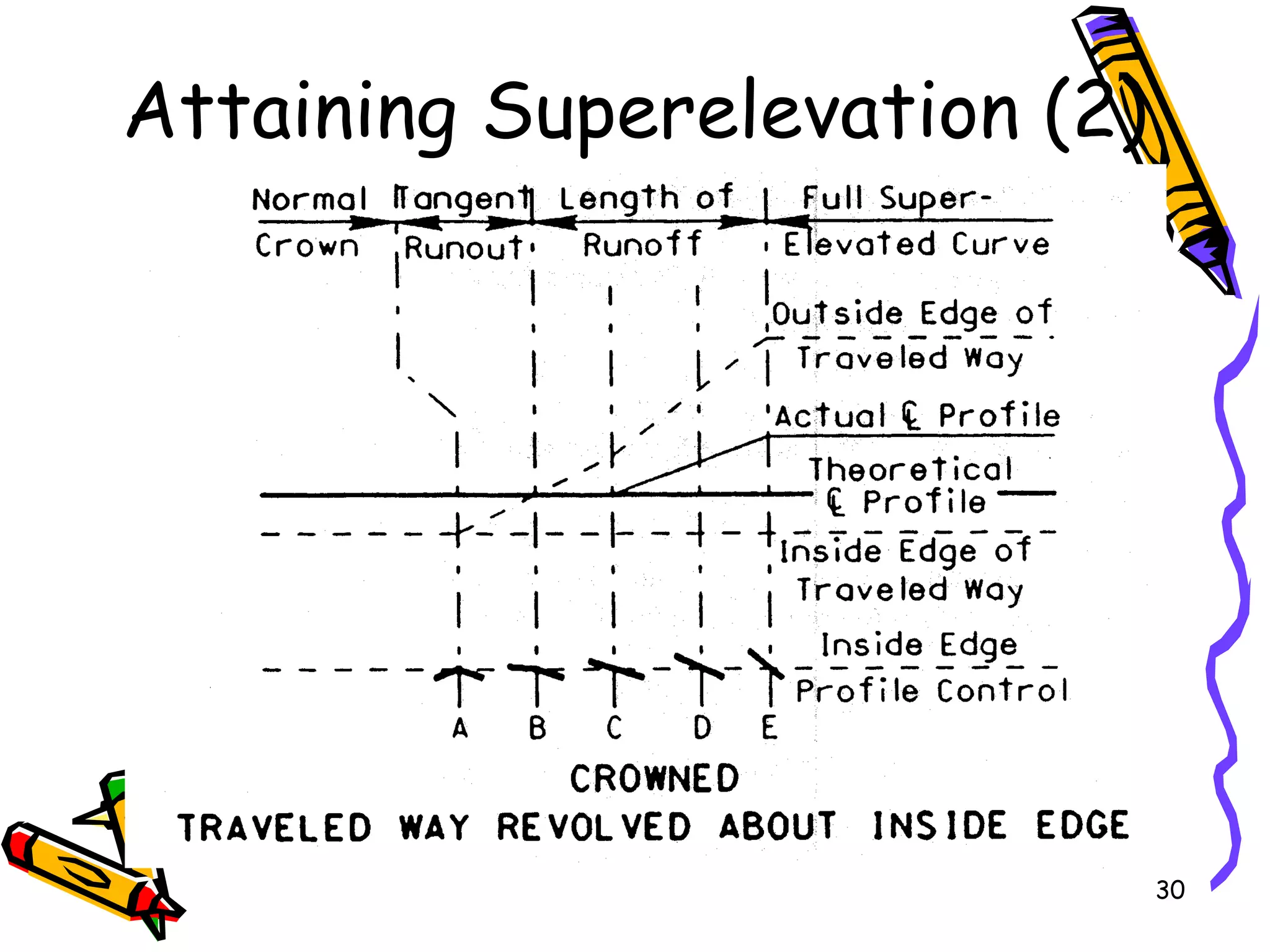
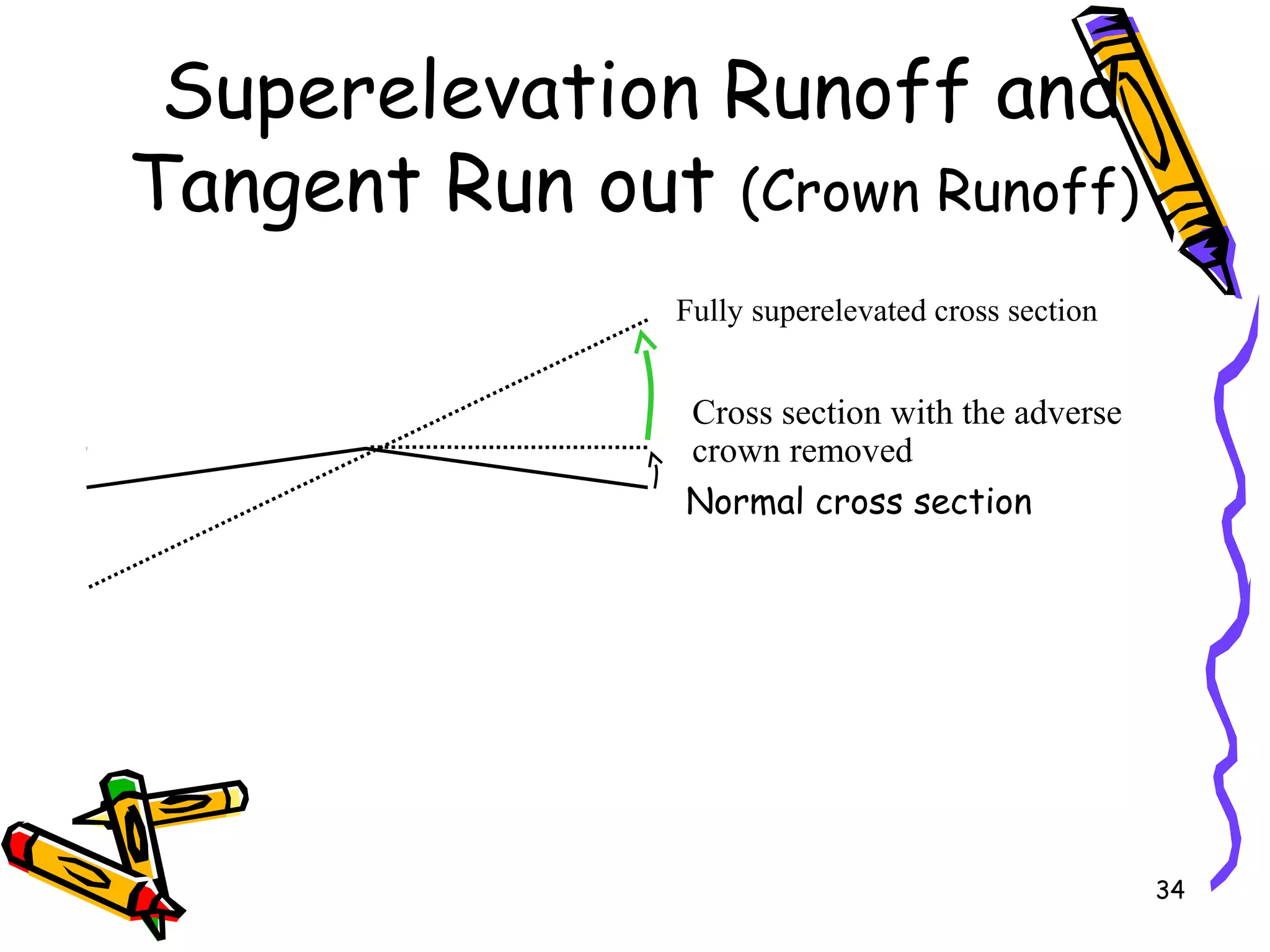
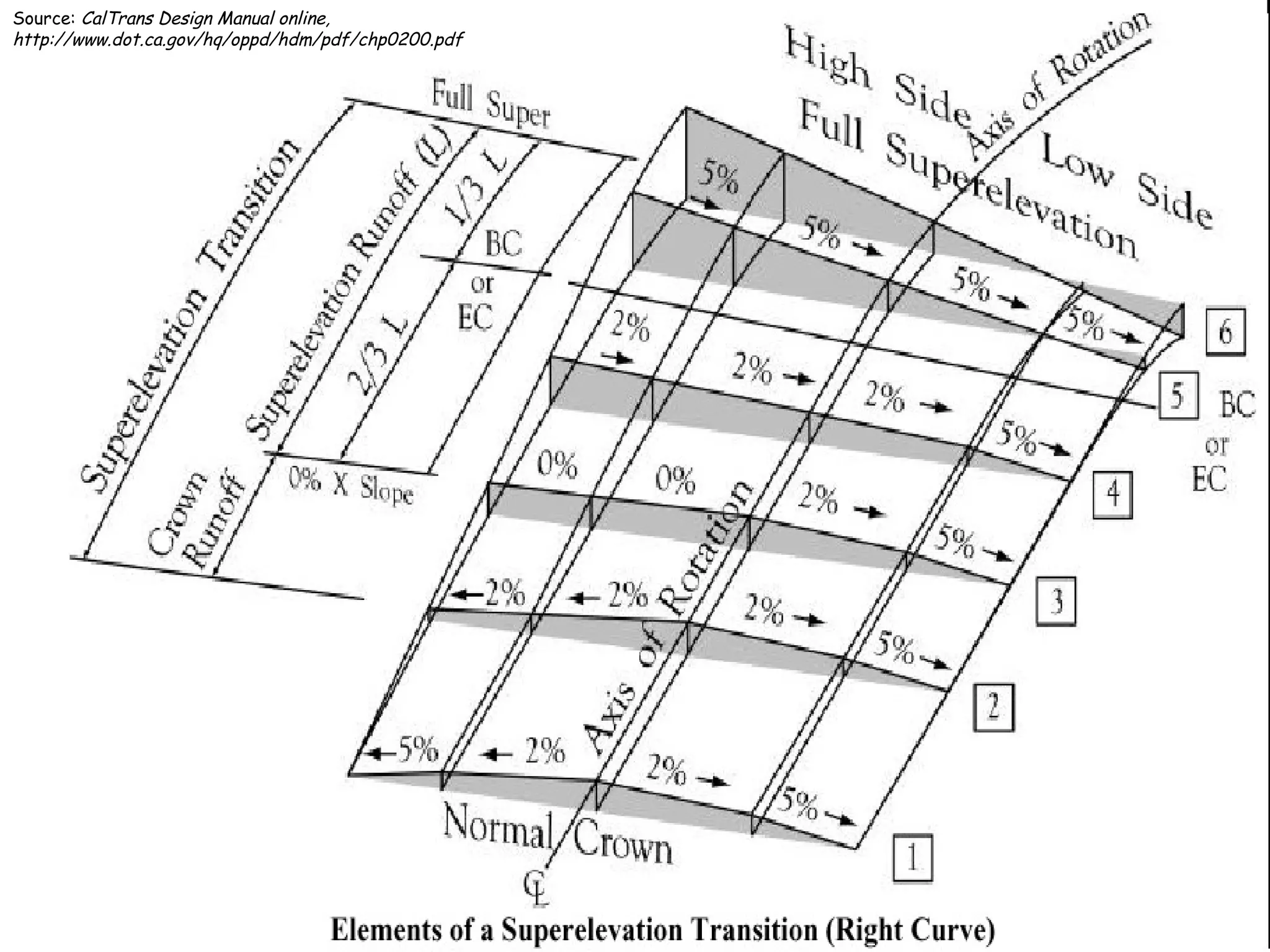
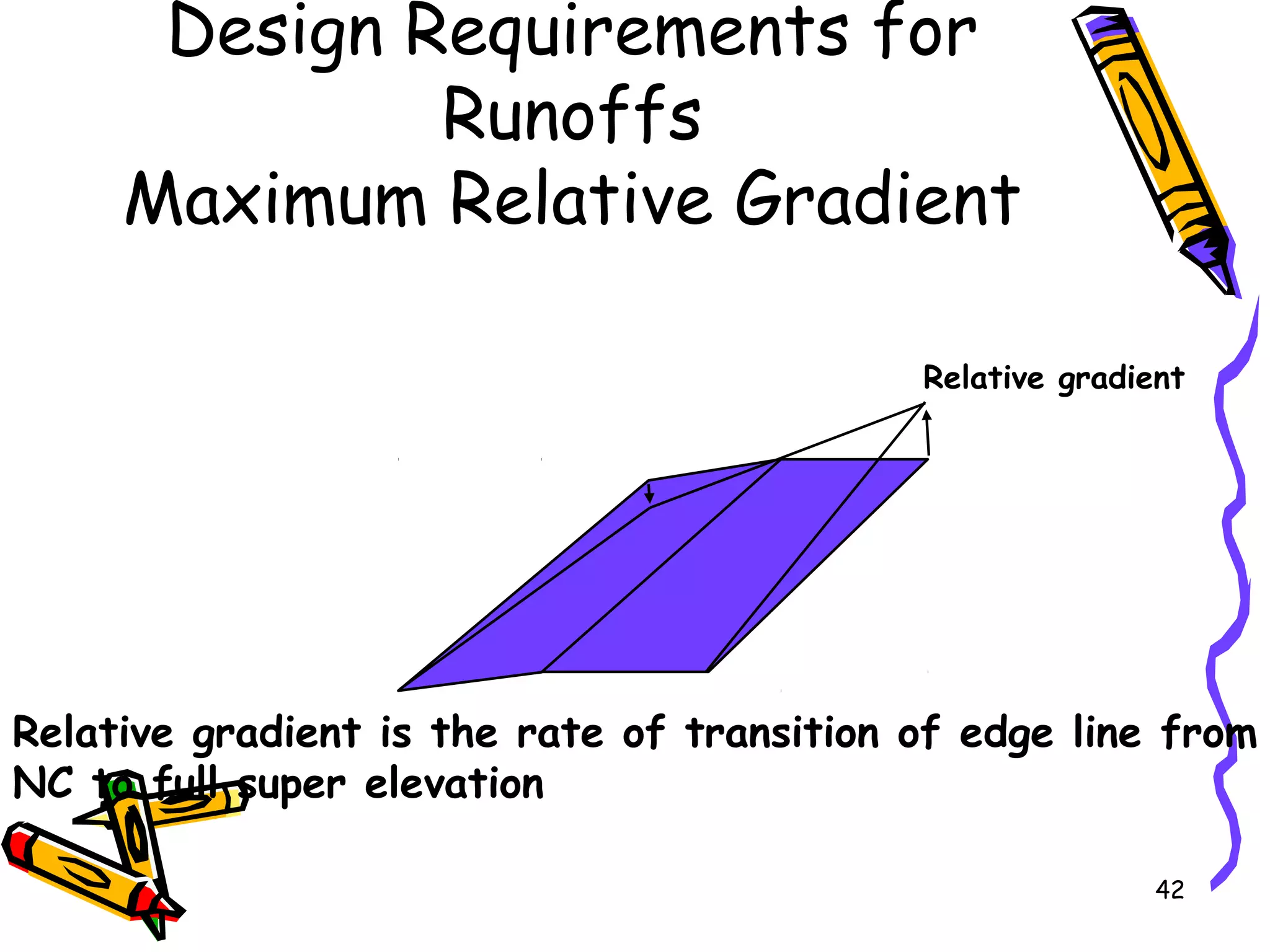
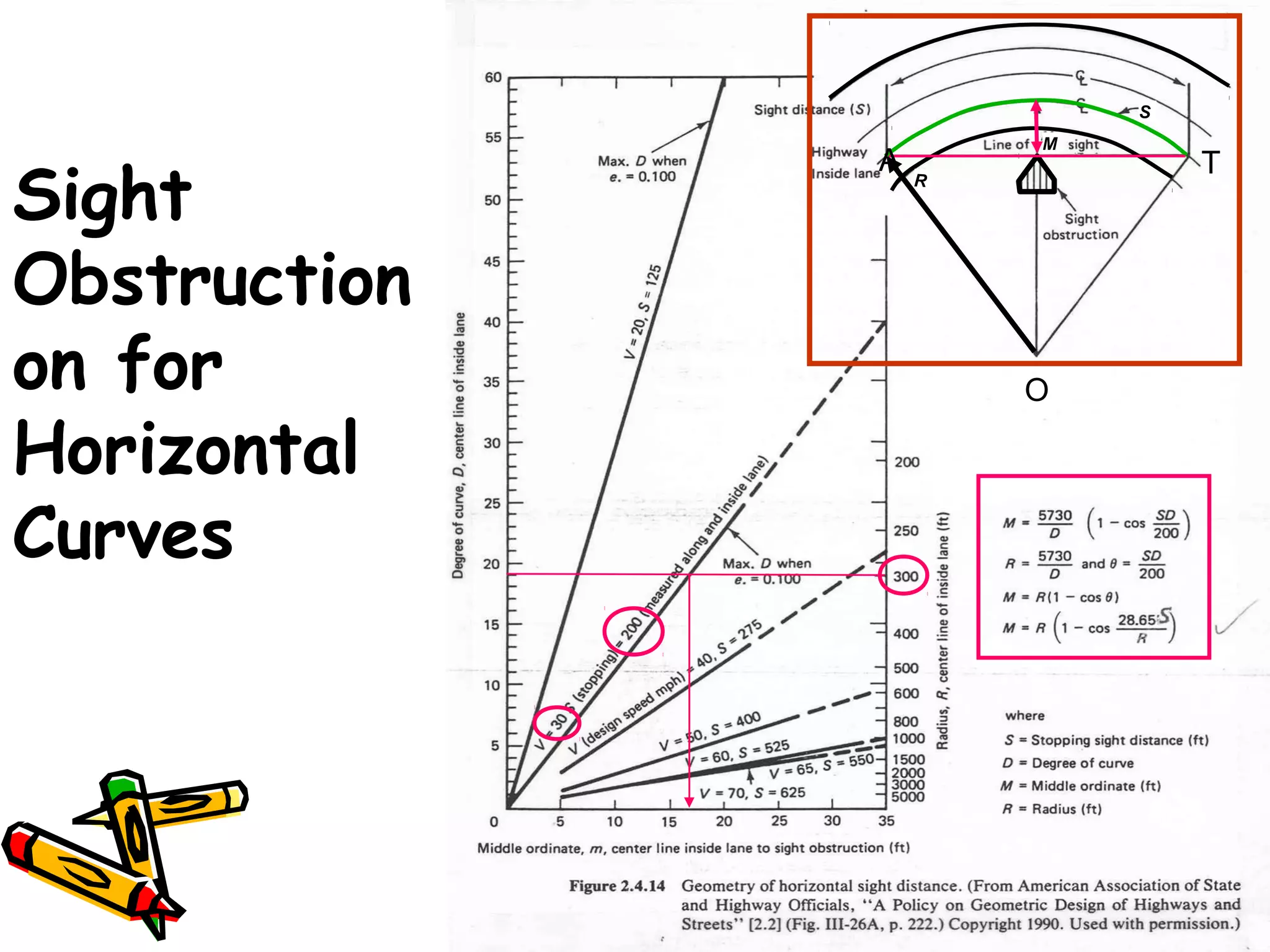
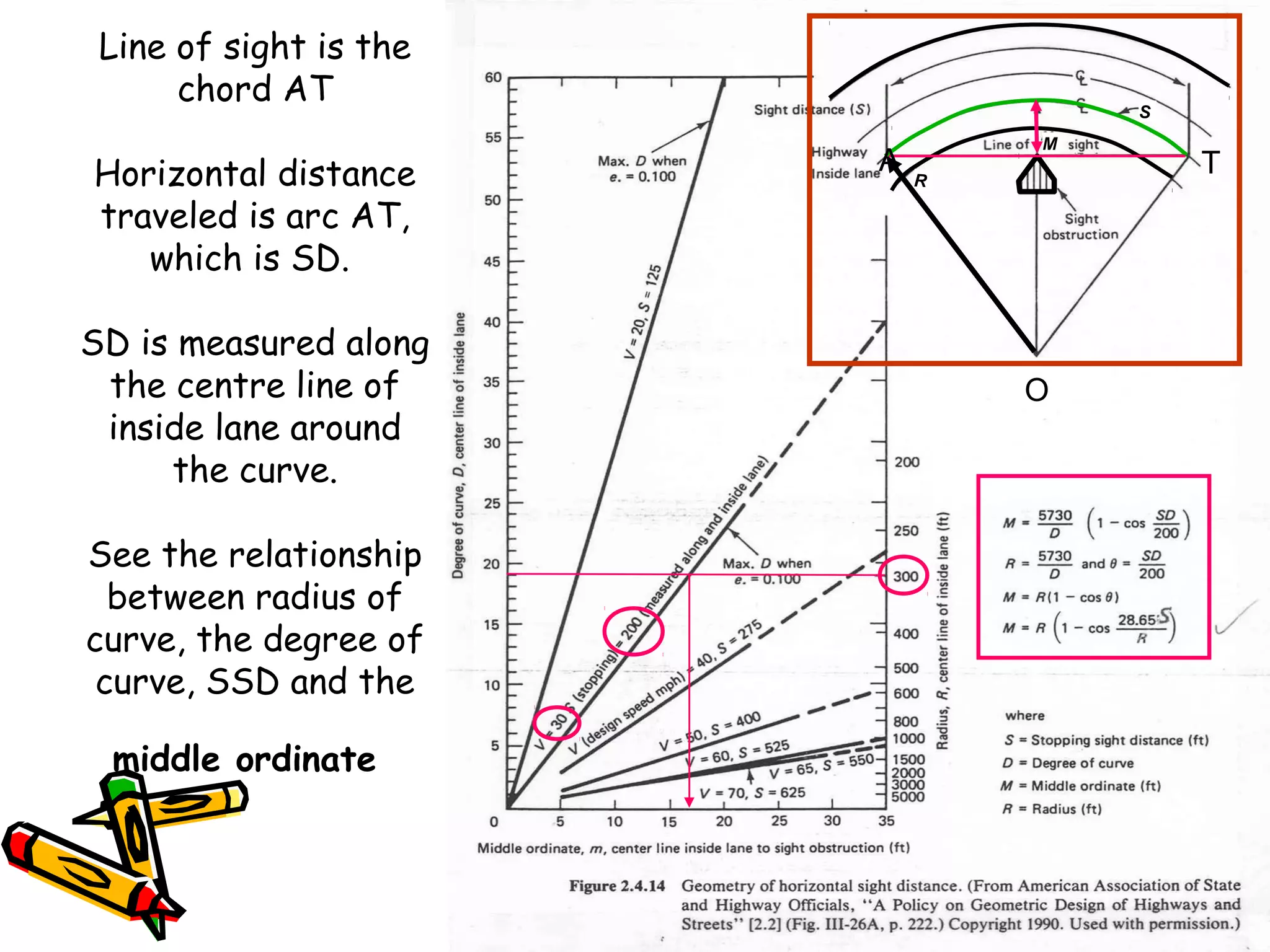
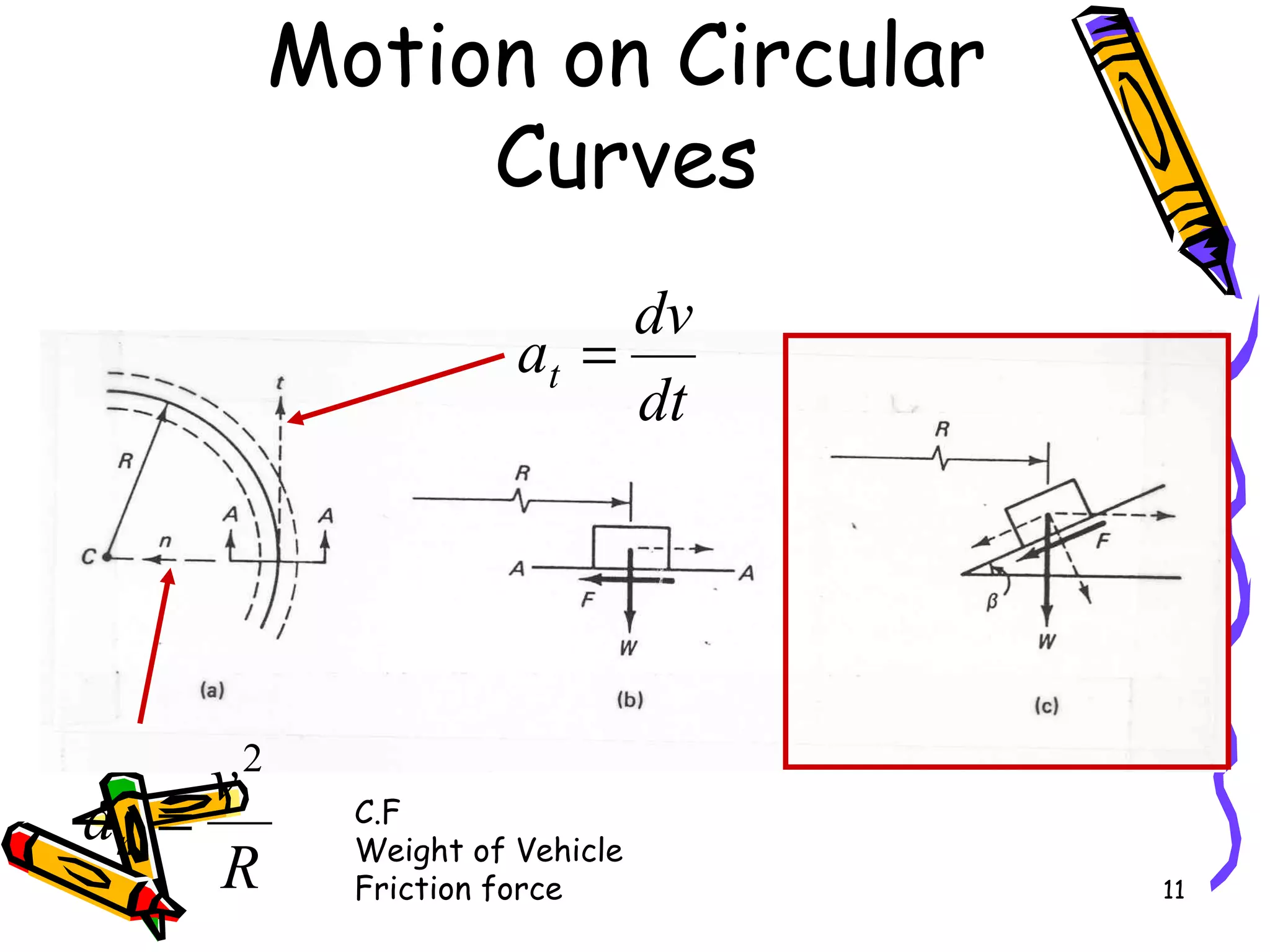
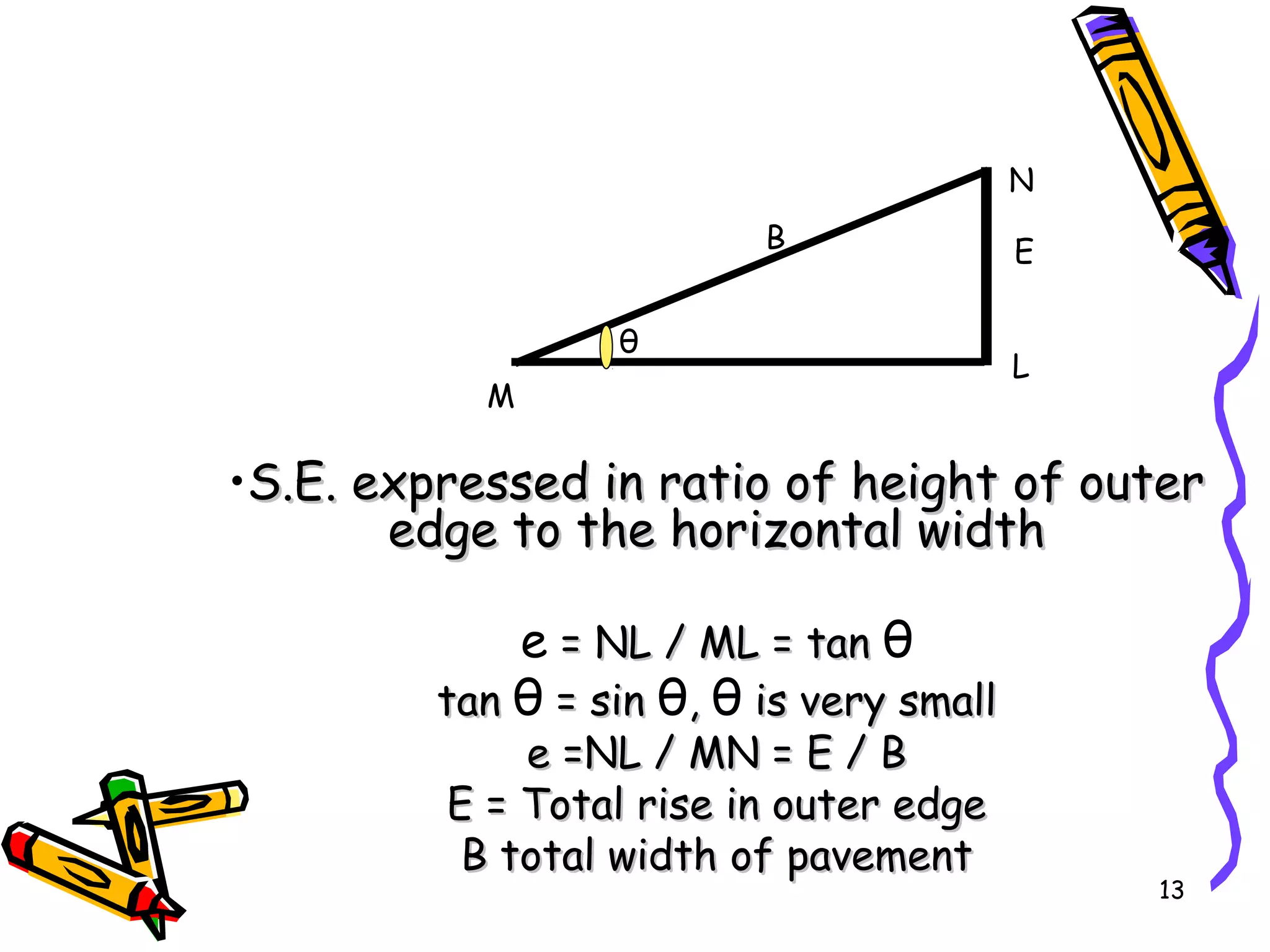
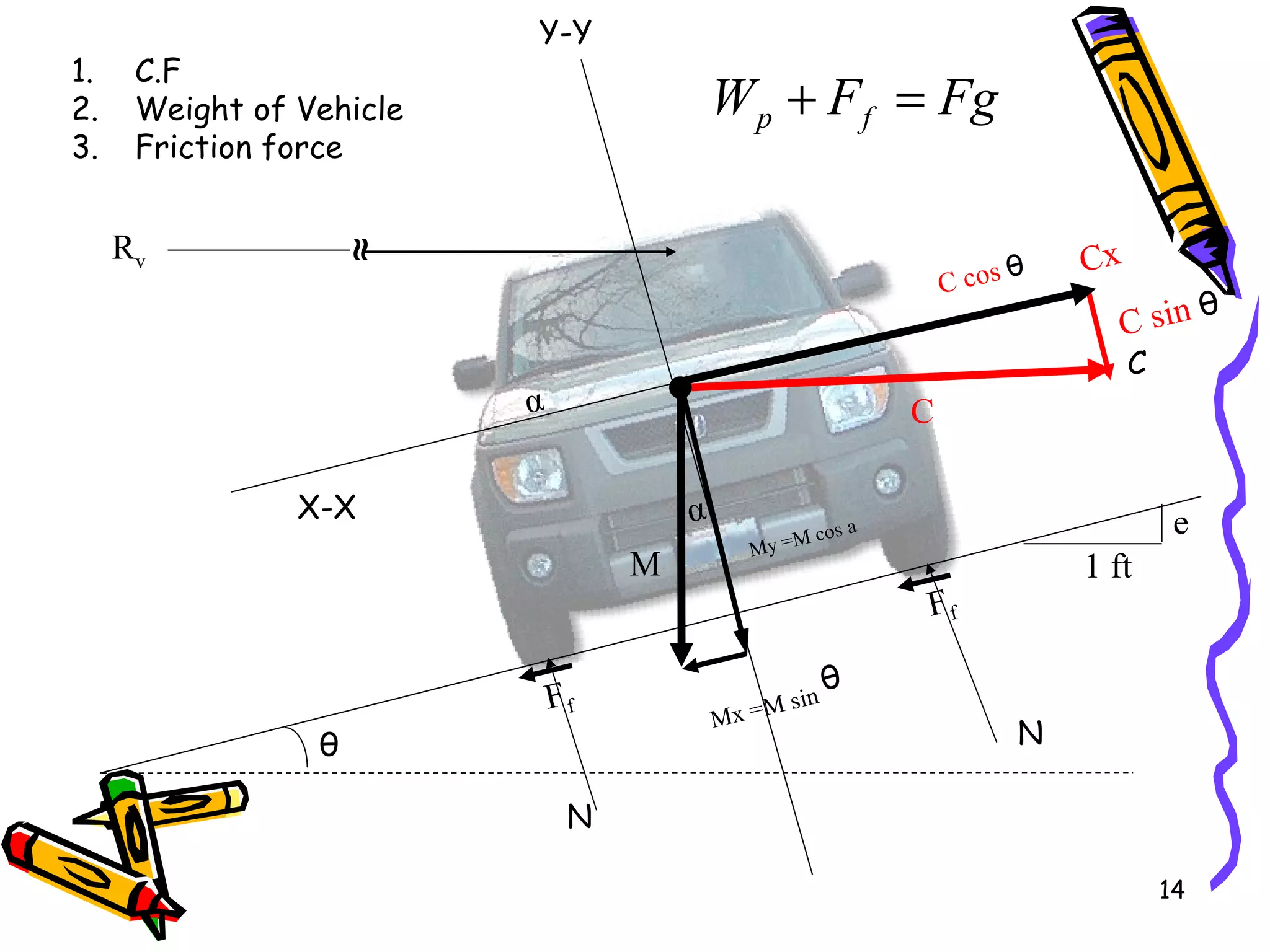
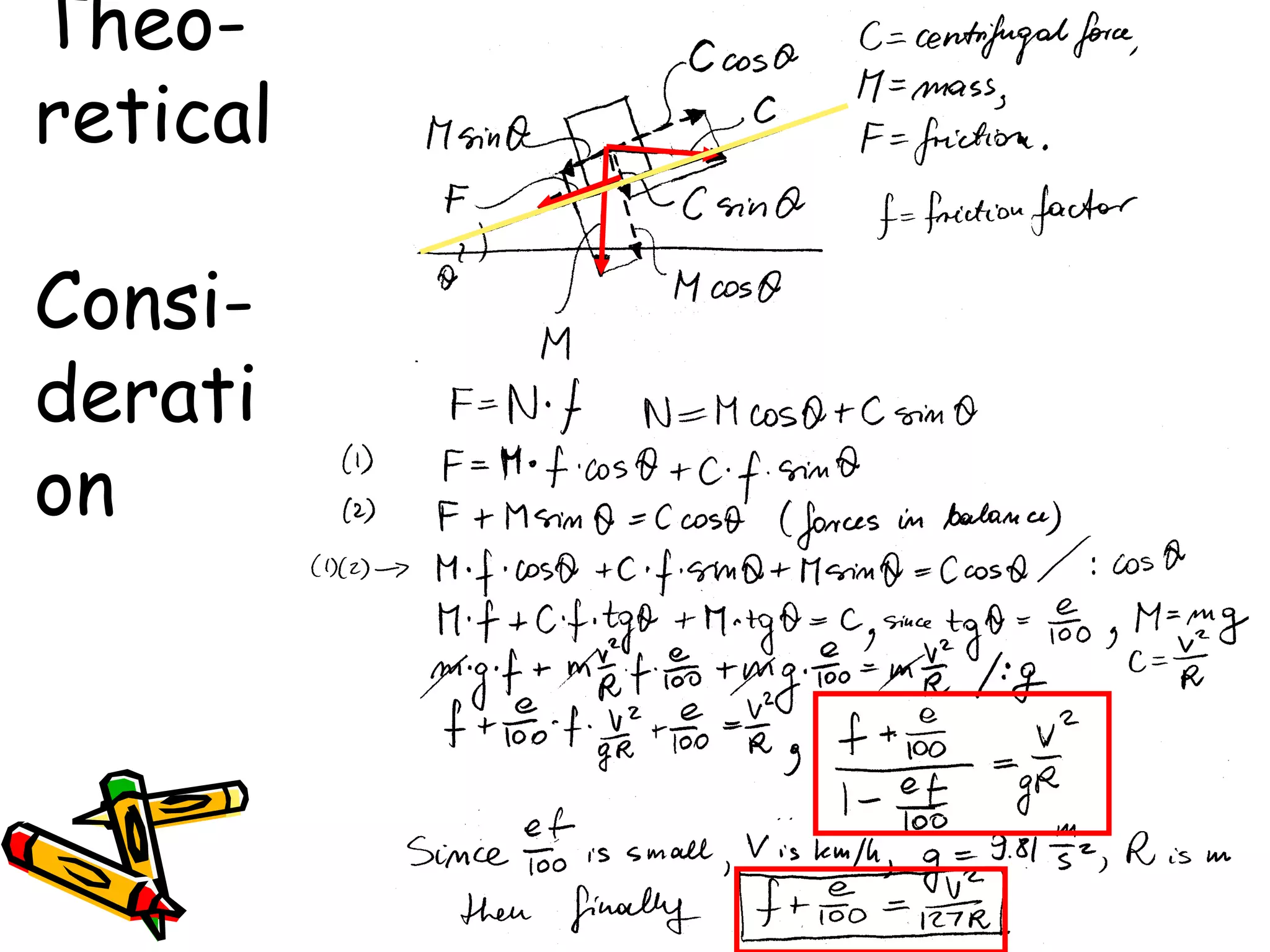
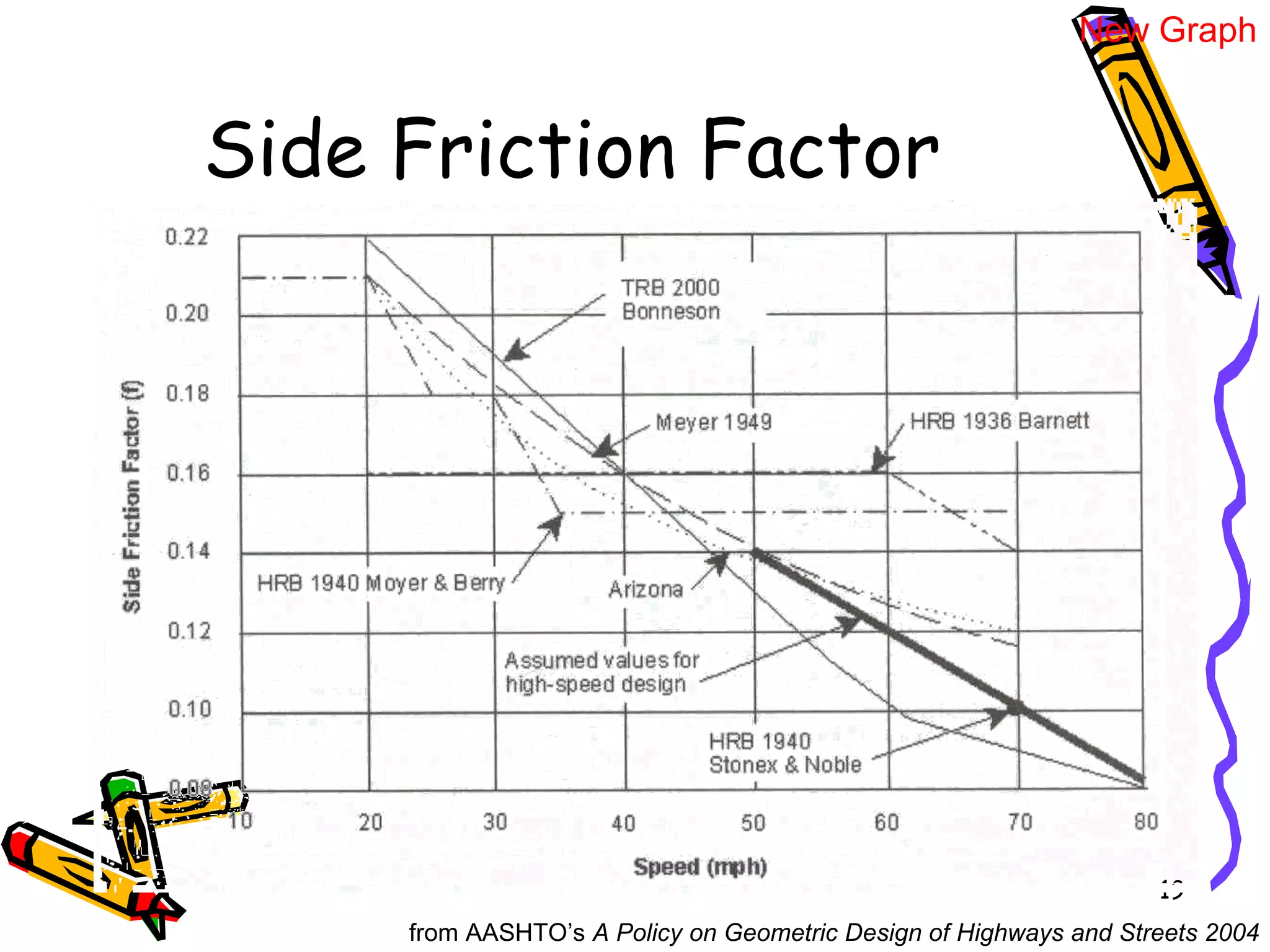
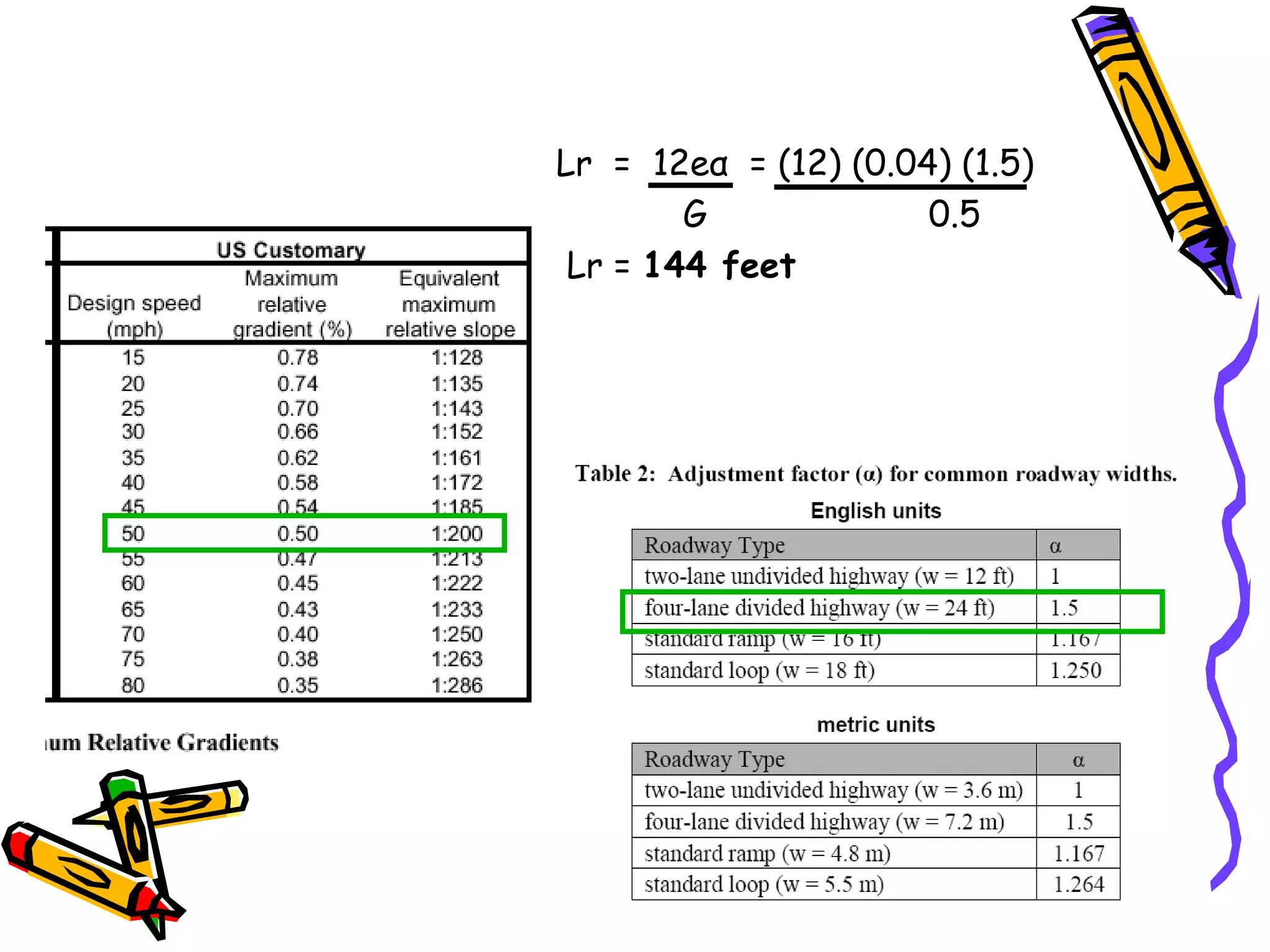
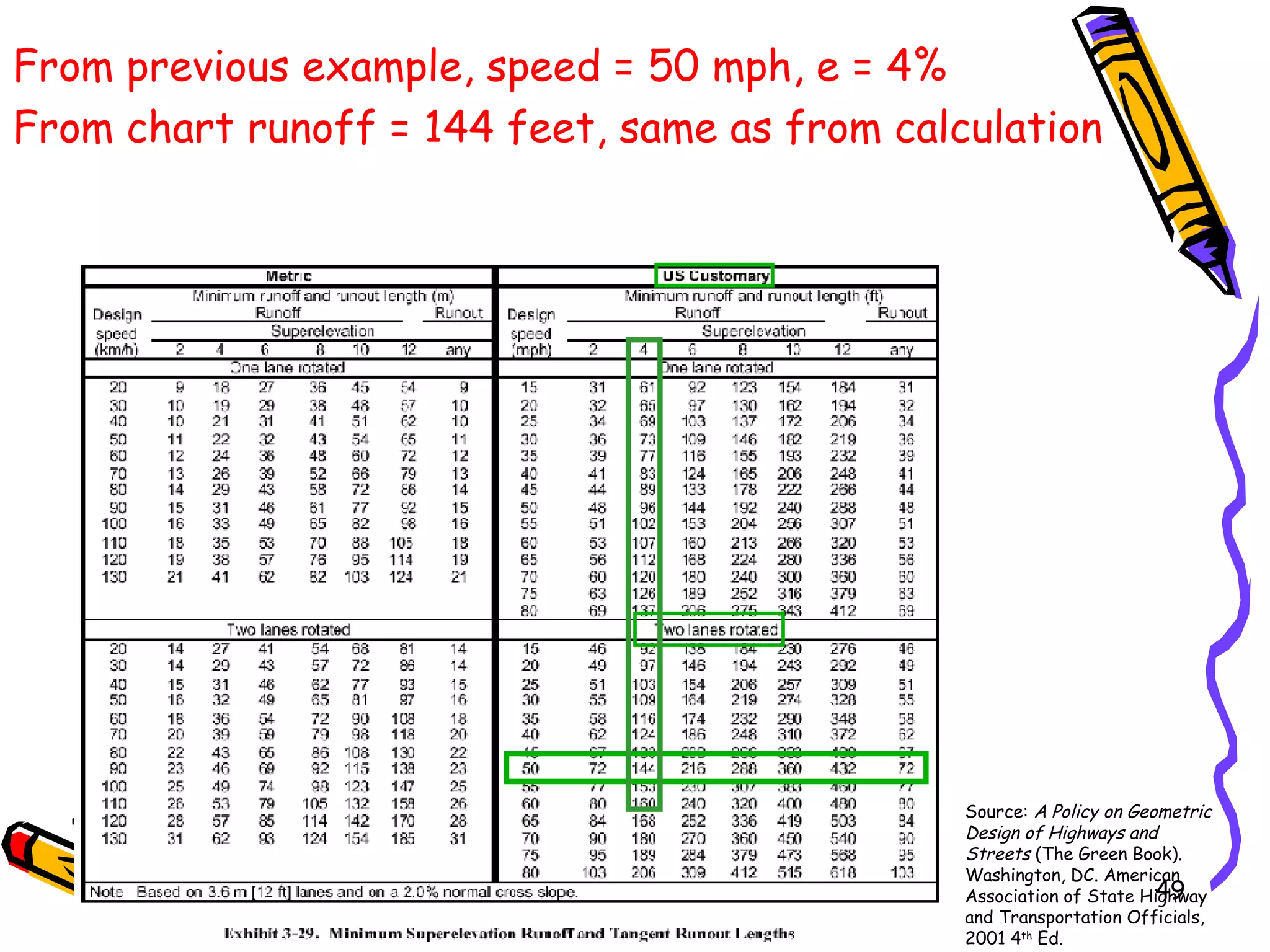
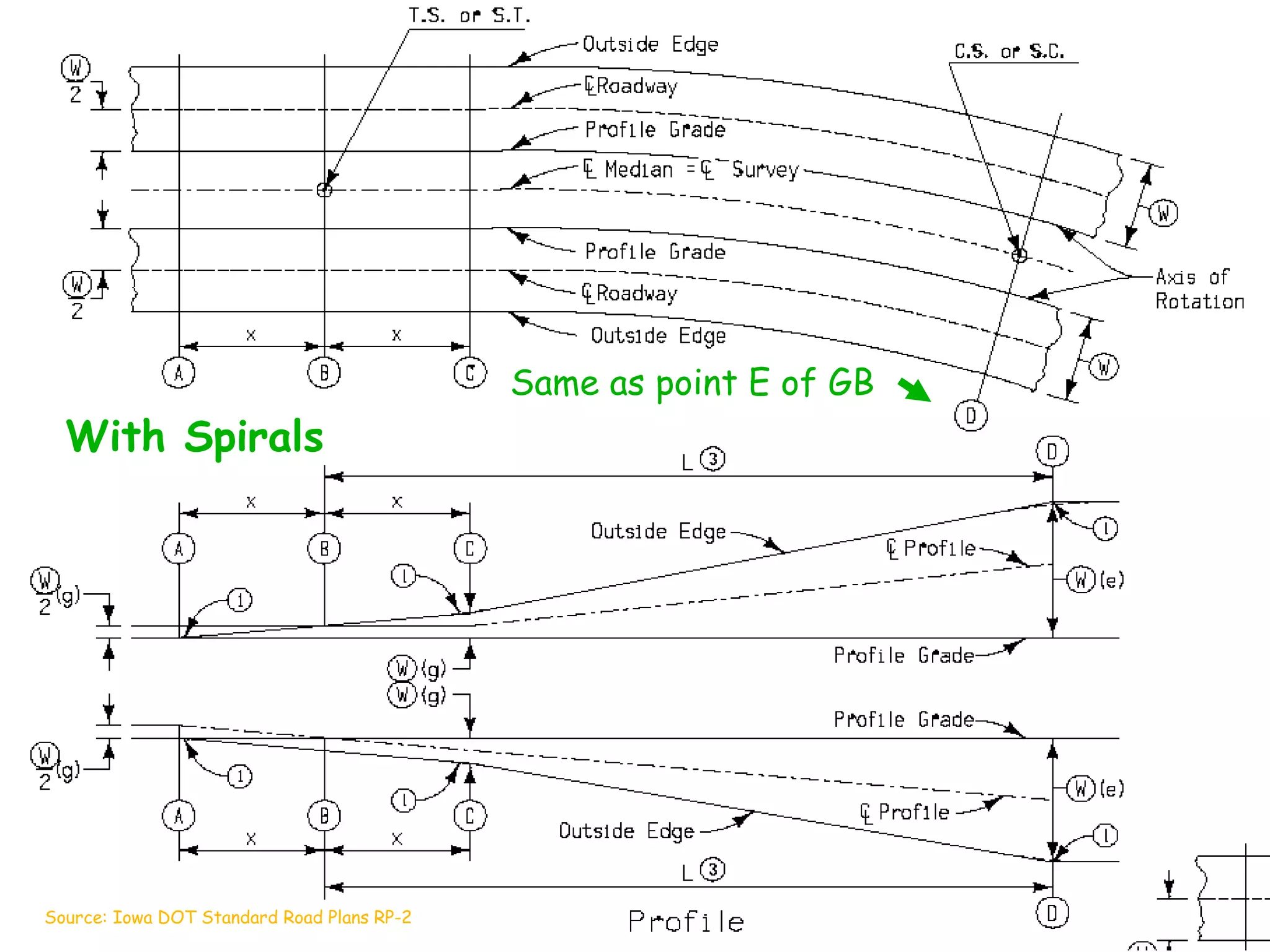
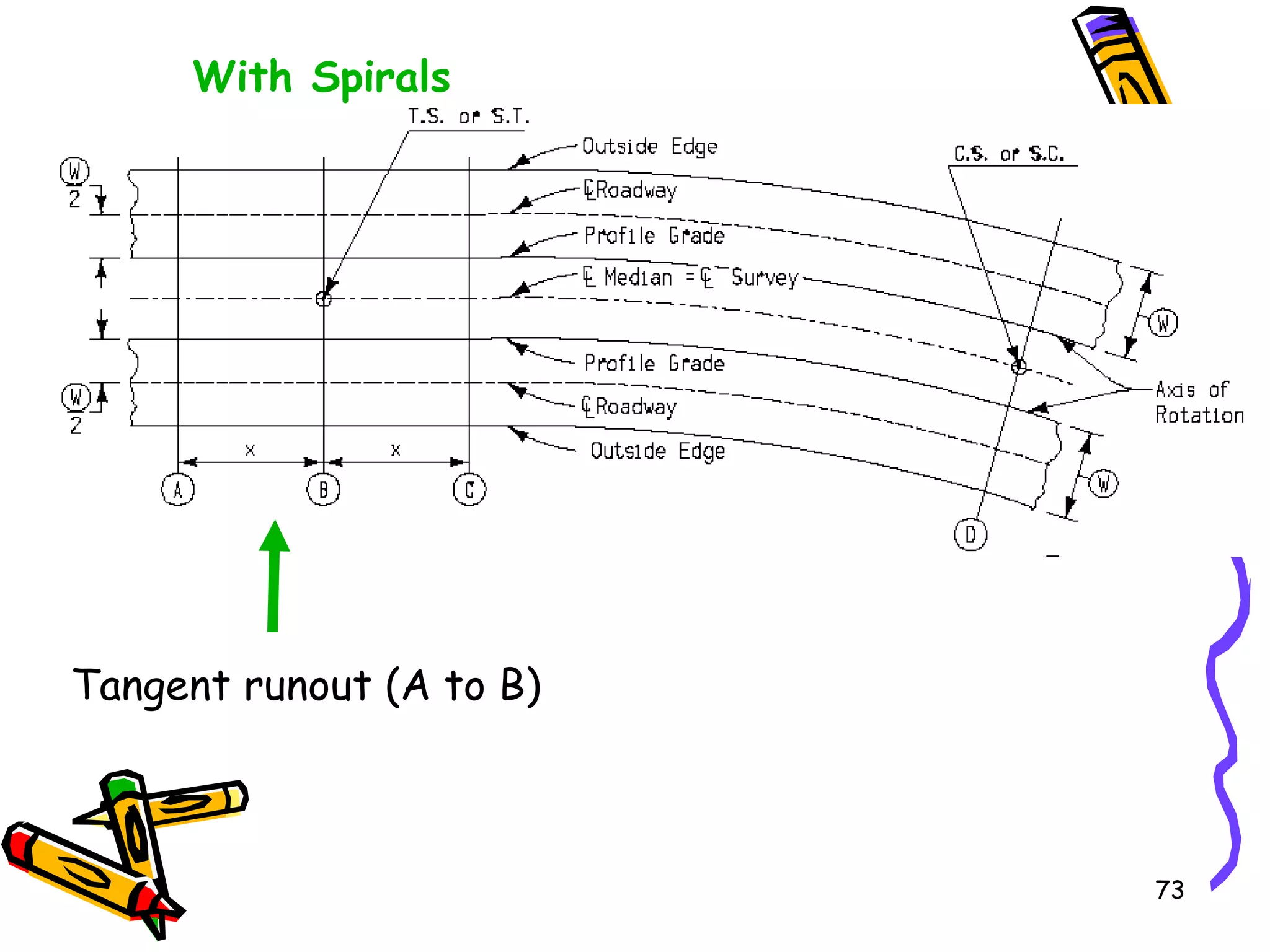
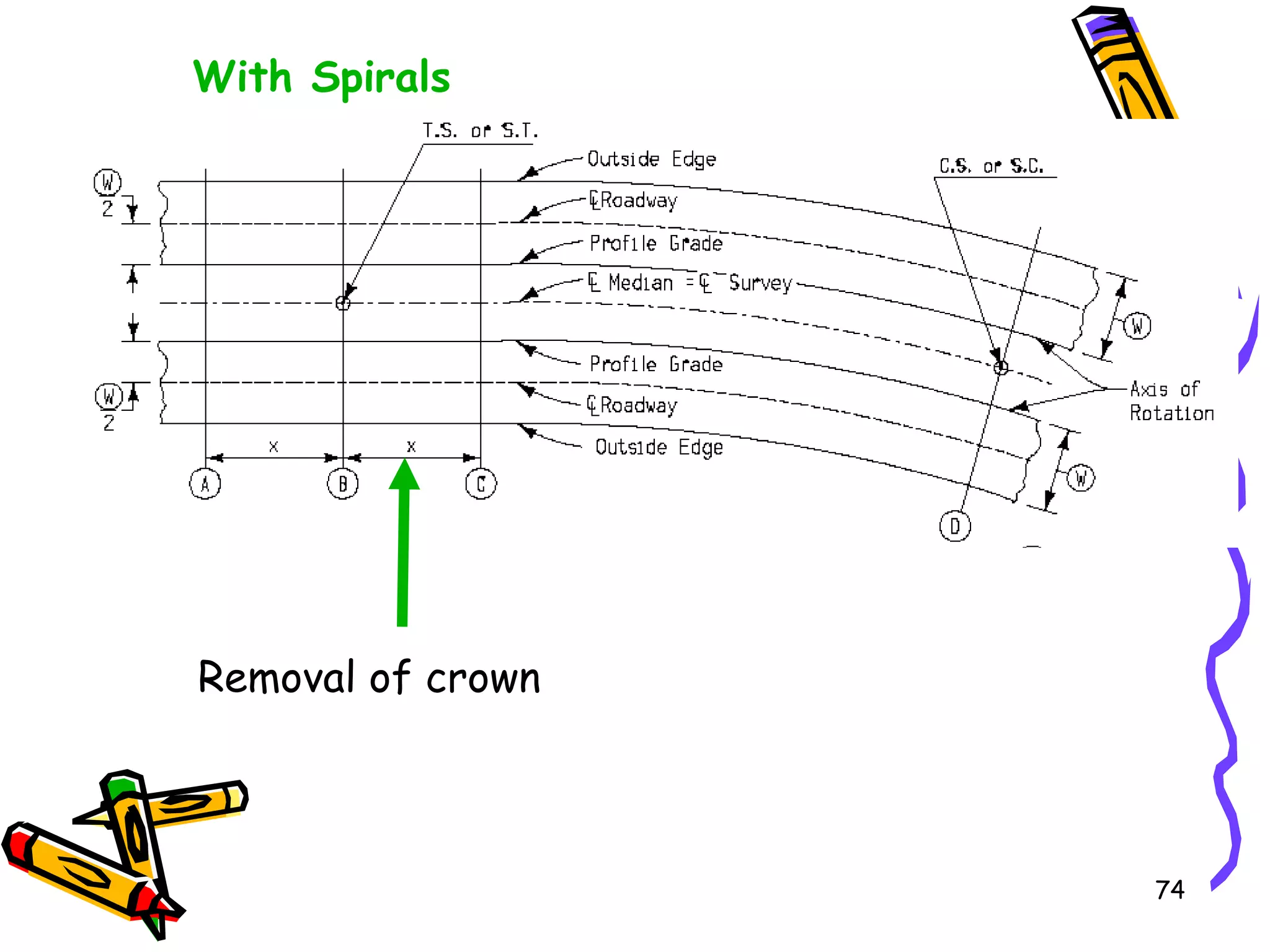
This document discusses sight distance and horizontal curves, superelevation, and transition curves. It provides the following key points: 1. Sight distance must be provided on horizontal curves to avoid obstructions. The middle ordinate equation calculates the maximum distance an obstruction can be from the centerline while maintaining sight distance. 2. Superelevation is used on curves to counteract centrifugal force. It is expressed as a ratio of outer edge height to width. Maximum rates vary from 4-12% depending on conditions. 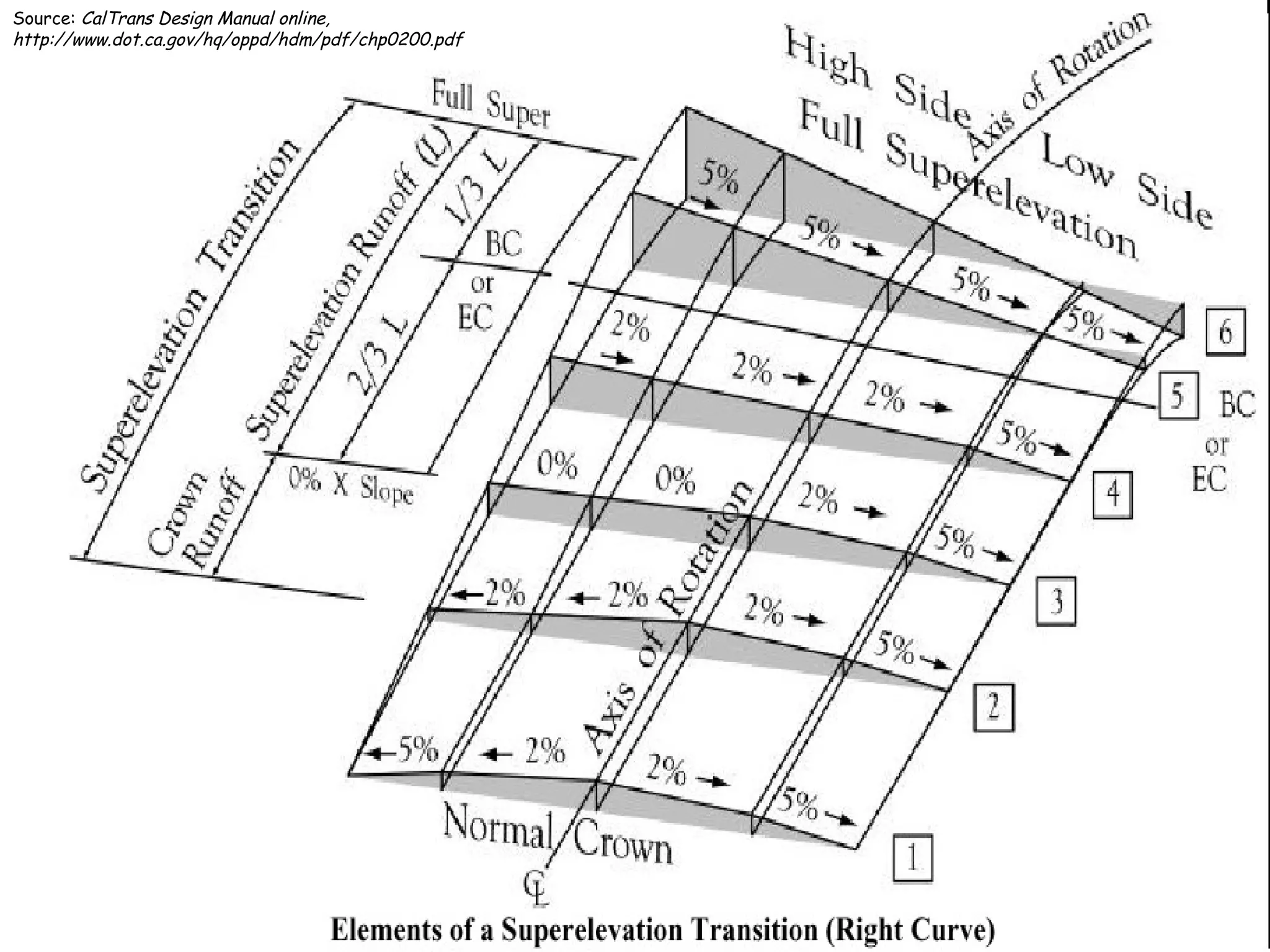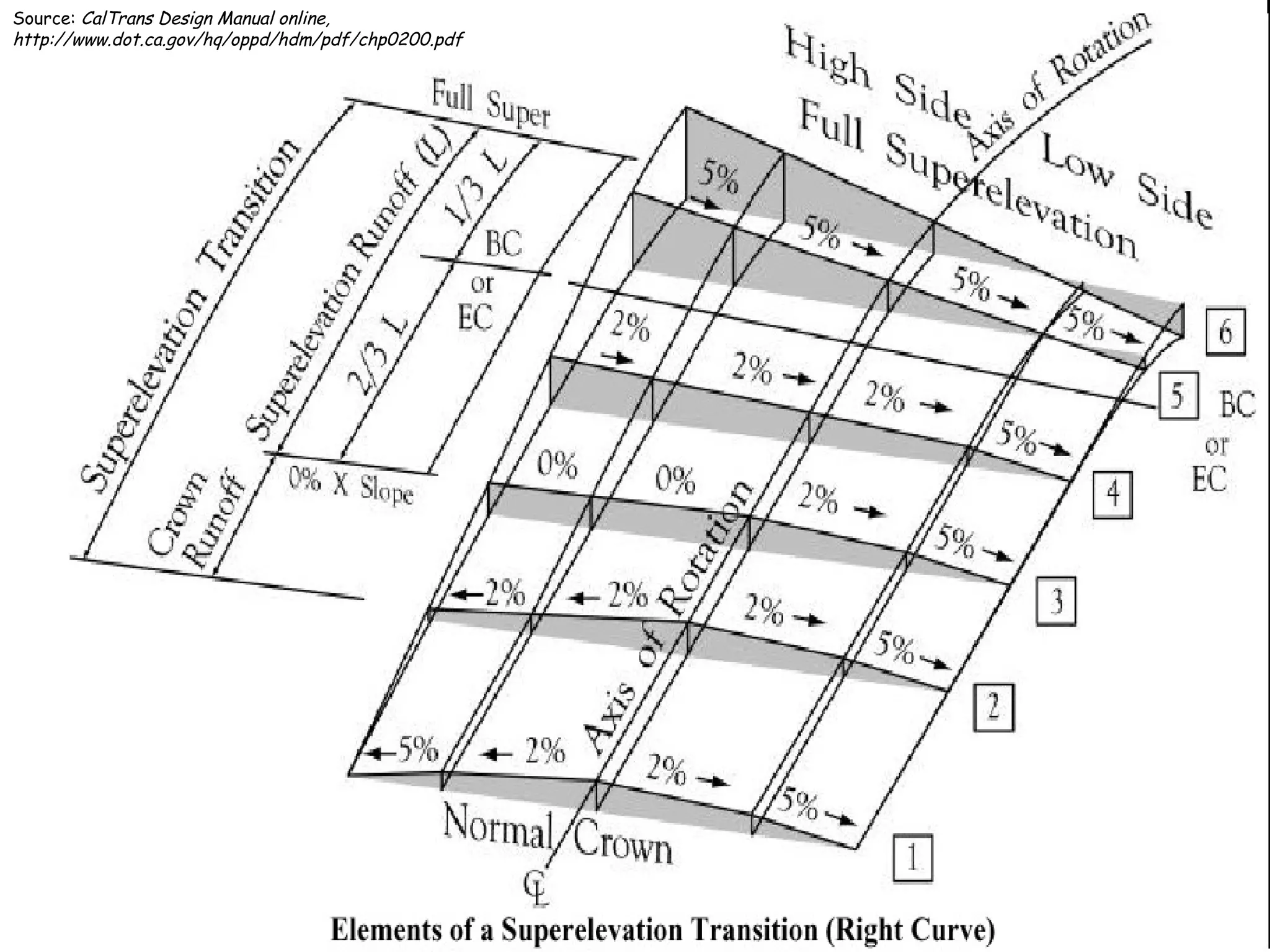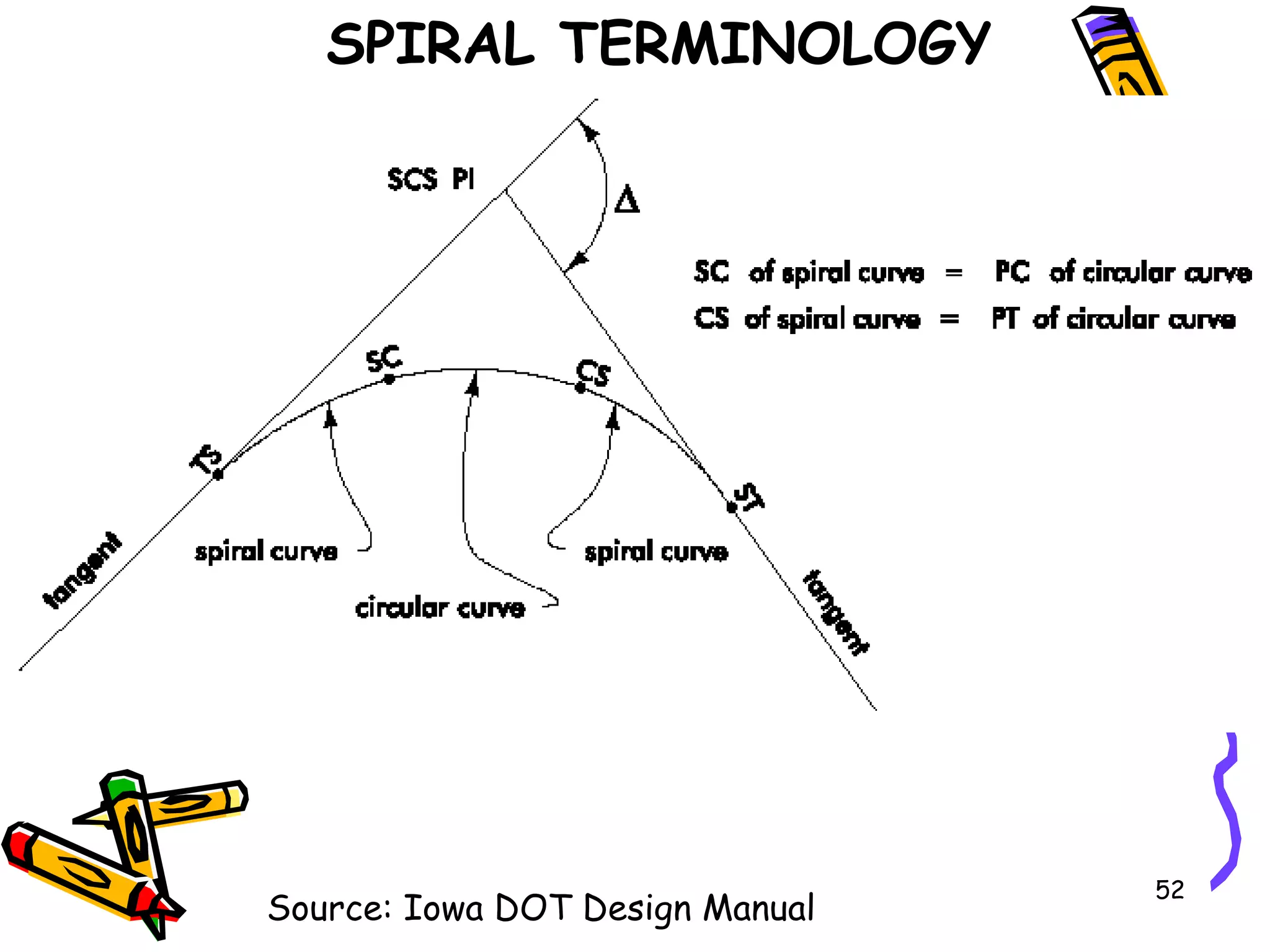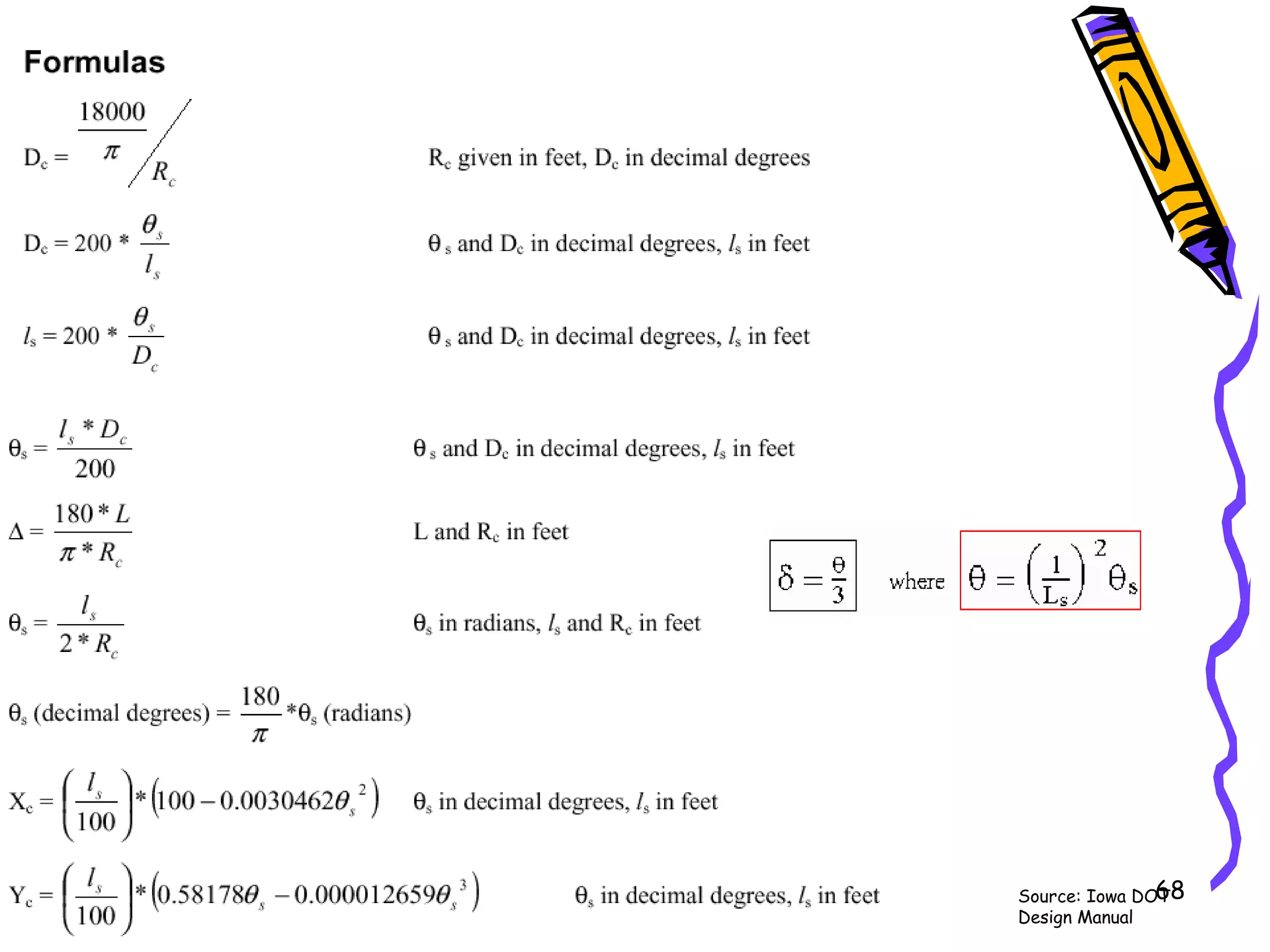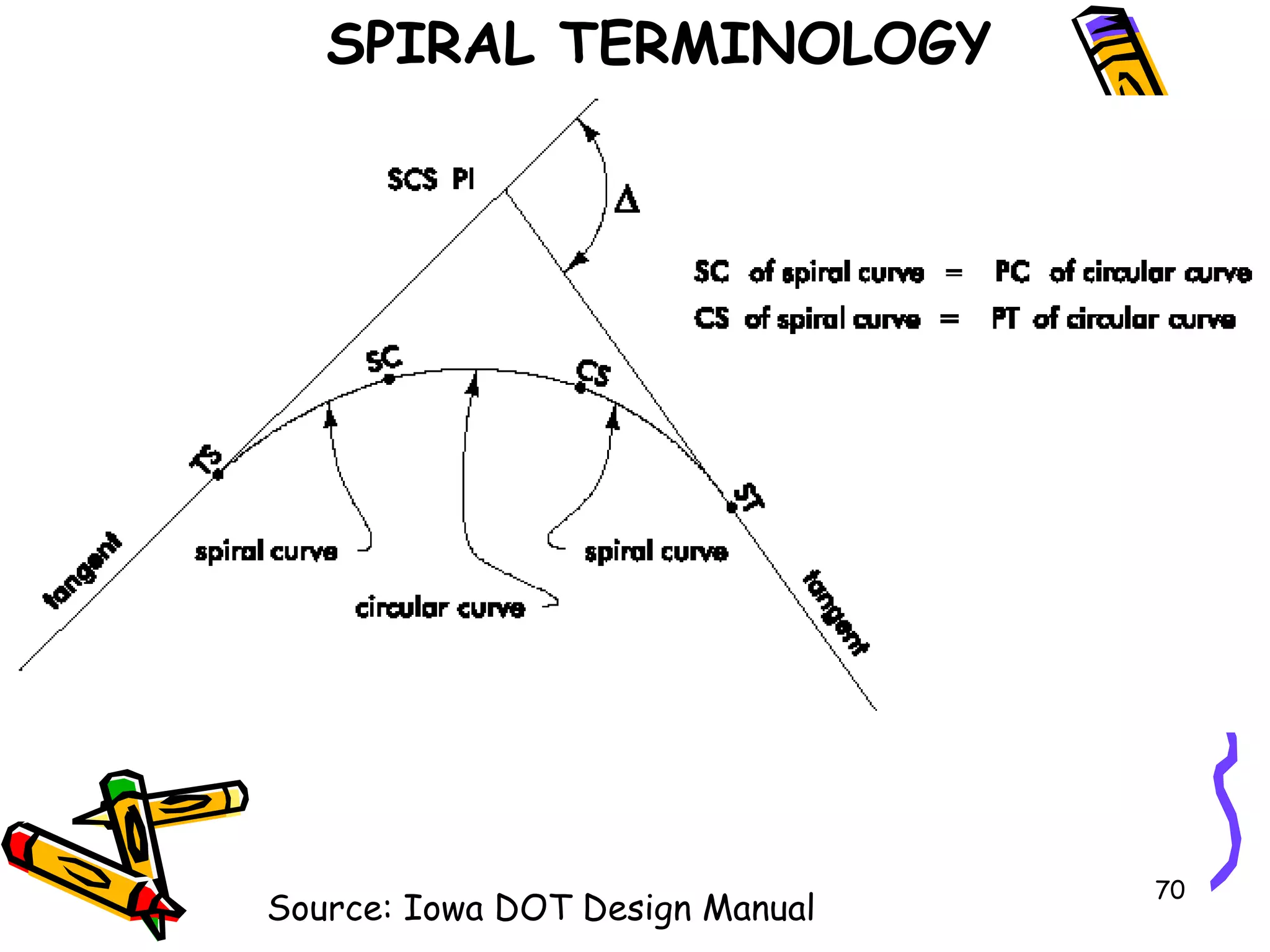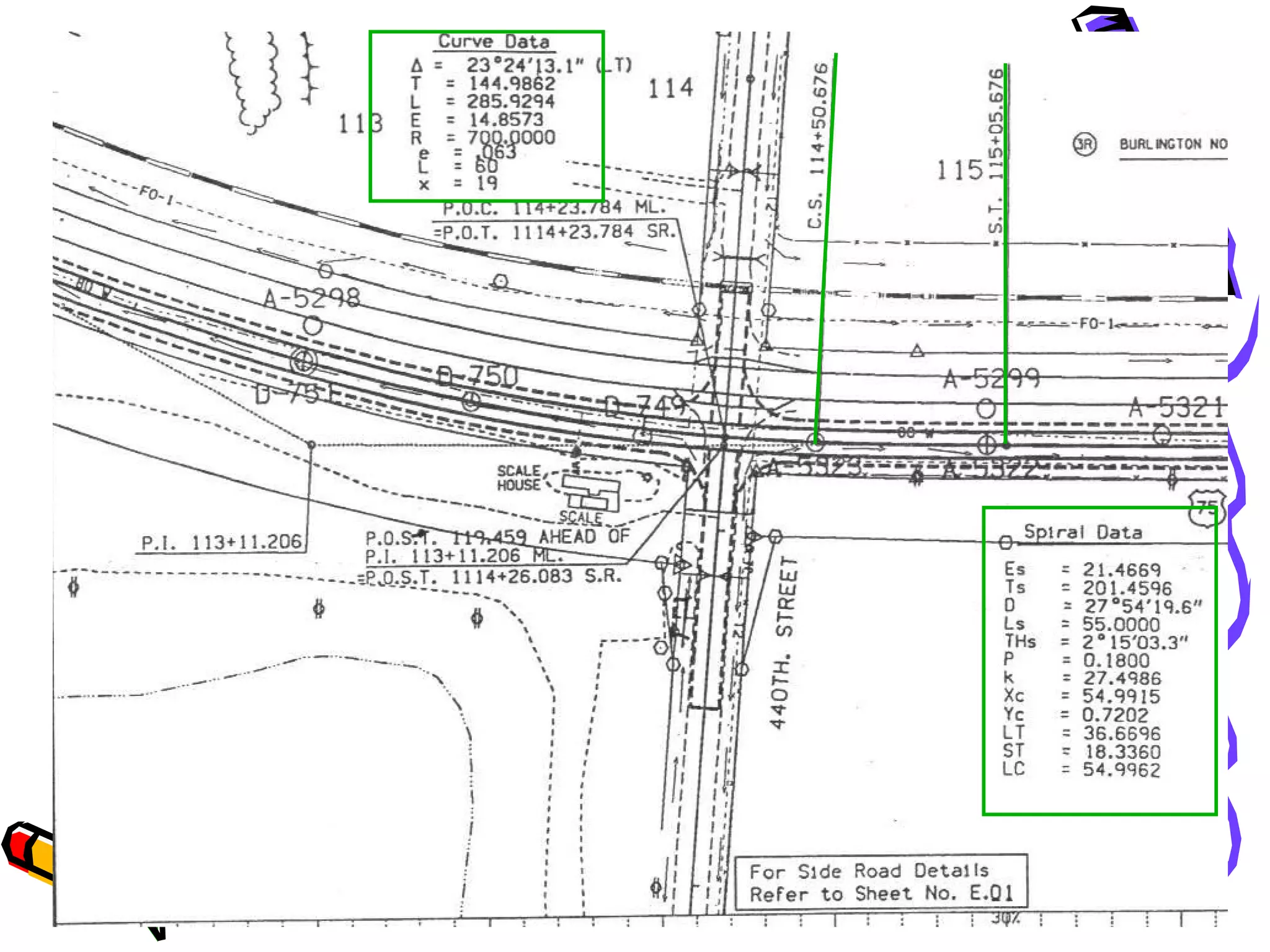3. Transition curves like spirals are used between tangents and curves to gradually change the radius. Their minimum length is calculated using equations involving design speed, radius, and rate

1. Sight Distance forSight Distance for
Horizontal CurvesHorizontal Curves
1

2. Provided Sight Distance
• Potential sight obstructions
– On horizontal curves: barriers,
bridge-approach fill slopes, trees,
back slopes of cut sections
– On vertical curves: road surface at
some point on a crest vertical
curve, range of head lights on a sag
curve

3. 3
S
R
M
O
TA
Sight
Obstruction
on for
Horizontal
Curves

4. 4
Line of sight is the
chord AT
Horizontal distance
traveled is arc AT,
which is SD.
SD is measured along
the centre line of
inside lane around
the curve.
See the relationship
between radius of
curve, the degree of
curve, SSD and the
middle ordinate
S
R
M
O
TA

5. 5
Middle ordinate
• Location of object along chord length that
blocks line of sight around the curve
• m = R(1 – cos [28.65 S])
R
Where:
m = line of sight
S = stopping sight distance
R = radius

6. 6
Middle ordinate
• Angle subtended at centre of circle by
arc AT is 2θ in degree then
• S / πR = 2θ / 180
• S = 2R θπ / 180
• θ = S 180 / 2R π = 28.65 (S) / R
• R-M/R = cos θ
• M = [1 – cos 28.65 (S) / R ]
θR
M
A T
B
T
O
θ

7. 7
Sight Distance Example
A horizontal curve with R = 800 ft is part of
a 2-lane highway with a posted speed limit
of 35 mph. What is the minimum distance
that a large billboard can be placed from
the centerline of the inside lane of the
curve without reducing required SSD?
Assume p/r =2.5 and a = 11.2 ft/sec2
SSD = 1.47vt + _________v2
____
30(__a___ ± G)
32.2

8. 8
Sight Distance Example
SSD = 1.47(35 mph)(2.5 sec) +
_____(35 mph)2
____ = 246 feet
30(__11.2___ ± 0)
32.2

9. 9
Sight Distance Example
m = R(1 – cos [28.65 S])
R
m = 800 (1 – cos [28.65 {246}])= 9.43’
800
(in radians not degrees)

10. 10
SuperelevationSuperelevation
DR ABDUL SAMI QURESHIDR ABDUL SAMI QURESHI
M
L
N
a
E
B

11. 11
Motion on Circular
Curves
dt
dv
at =
R
v
an
2
= C.F
Weight of Vehicle
Friction force

12. 12
Definition
• The transverse slope provided by
raising outer edge w.r.t. inner edge
• To counteract the effects of C.
Force (overturning/skid laterally)
L
N
a
EB
M

13. 13
•S.E. expressed in ratio of height of outerS.E. expressed in ratio of height of outer
edge to the horizontal widthedge to the horizontal width
e = NL / ML = tan= NL / ML = tan θ
tantan θ = sin= sin θ,, θ is very smallis very small
e =NL / MN = E / Be =NL / MN = E / B
E = Total rise in outer edgeE = Total rise in outer edge
B total width of pavementB total width of pavement
M
L
N
θ
EB

14. 14
FgFW fp =+
α
α
C cos θ Cx
Mx =M sin
θ
My =M cos a
Ff
Ff
θ
C
M 1 ft
e
≈
Rv
1. C.F
2. Weight of Vehicle
3. Friction force
X-X
Y-Y
C
N
N
C sin θ

15. 15
Theo-
retical
Consi-
derati
on

16. 16
Vehicle Stability on Curves
where:
gR
v
fe s
2
=+
(ft/s),speeddesign=v
(-),tcoefficienfrictionside=sf
).ft/s(32onacceleratigravity 2
=g
(-),tionsupereleva=e
(ft),radius=R
Assumed
Desig
n
speed
(mph)
Maximum
design
fs max
20 0.17
70 0.10
Must not be too short
(0.12)0.10-0.06max =e

17. 17
Selection of e and fs
• Practical limits on super elevation (e)
– Climate
– Constructability
– Adjacent land use
• Side friction factor (fs) variations
– Vehicle speed
– Pavement texture
– Tire condition
• The maximum side friction factor is the point at
which the tires begin to skid
• Design values of fs are chosen somewhat below
this maximum value so there is a margin of safety

18. 18

19. 19
Side Friction Factor
from AASHTO’s A Policy on Geometric Design of Highways and Streets 2004
New Graph

20. 20
Maximum Superelevation
• Superelevation cannot be too large since an
excessive mass component may push slowly
moving vehicles down the cross slope.
• Limiting values emax
– 12 % for regions with no snow and ice conditions
(higher values not allowed),
– 10 % recommended value for regions without
snow and ice conditions,
– 8% for rural roads and high speed urban roads,
– 4, 6% for urban and suburban areas.

21. 21
Example
• A section of road is being designed as a high-speed highway.
The design speed is 70 mph. Using AASHTO standards,
what is the maximum super elevation rate for existing curve
radius of 2500 ft and 300 ft for safe vehicle operation?
• Assume the maximum super elevation rate for the given
region is 8%.
• max e = ?
• For 70 mph, f = 0.10
• 1. 2500 = V2/15(fs+e) = (70 )2/(0.10 + e) = 0.0306
• e = 3%
• 2. 300 = V2/(fs+e) = (70 x 1.47)2/32.2(0.10 + e) = 0.988
• e = 9.8%

22. • 300 = V2/g(fs+e) = (70)2/15(fs + 0.8)
• f = 1.008 > 0.10
• 300 = V2/15(fs+e) = (V )2/15(0.10+ 0.8)
• V = 28.46 mph
22

23. 23
Crown / super elevation
runoff length

24. 24
Source: CalTrans Design Manual online,
http://www.dot.ca.gov/hq/oppd/hdm/pdf/chp0200.pdf

25. 25
Attainment of Superelevation -
General
1. Tangent to superelevation
2. Must be done gradually over a distance without
appreciable reduction in speed or safety and
with comfort
3. Change in pavement slope should be consistent
over a distance
4. Methods (Exhibit 3-37 p. 186)
a. Rotate pavement about centerline
b. Rotate about inner edge of pavement
c. Rotate about outside edge of pavement

26. 26
Source: CalTrans Design Manual online,
http://www.dot.ca.gov/hq/oppd/hdm/pdf/chp0200.pdf

27. 27
Common methods of developing the
transition to super elevation
• At (2)the out side edge is far below the centre
line as the inside edge
• At (3)the out side edge has reached the level of
the centre line
• At point (4) the out side edge is located as far
above as the inside edge is below the centerline.
• Finally , at point (5) the cross section is fully
super elevated and remain through out the
circular curve
• The reverse of these profiles is found at the
other end of circular curve.

28. 28
Common methods of developing the
transition to super elevation
• Location of inside edge, centre line, and out side edge are
shown relative to elevation of centerline
• The difference in elevation being equal to the normal crown
times the pavement width.
• At A the out side edge is far below the centre line as the
inside edge
• At B the out side edge has reached the level of the centre
line
• At point C the out side edge is located as far above as the
inside edge is below the centerline.
• Finally , at point E the cross section is fully super elevated
• The reverse of these profiles is found at the other end of
circular curve.

29. 29
Attaining Superelevation (1)
•Location of inside edge, centre line, and out side edge are shown
relative to elevation of centerline

30. 30
Attaining Superelevation (2)

31. 31
Attaining Superelevation (3)

32. 32
Superelevation
Transition Section
• Tangent Runout (Crown Runoff)
Section + Superelevation Runoff
Section.
• Tangent runout = the length of highway
needed to change the normal cross section
to the cross section with the adverse crown
removed.

33. Super elevation runoff
• Super elevation runoff = the length of
highway needed to change the cross section
with the adverse crown removed to the
cross section fully super elevated.
33

34. 34
Superelevation Runoff and
Tangent Run out (Crown Runoff)
Normal cross section
Fully superelevated cross section
Cross section with the adverse
crown removed

35. 35
Location of Runout and
Runoff

36. 36
Tangent Runout Section
• Length of roadway needed to
accomplish a change in outside-lane
cross slope from normal cross
slope rate to zero
For rotation about
centerline

37. 37
Superelevation Runoff
Section
• Length of roadway needed to
accomplish a change in outside-lane
cross slope from 0 to full
superelevation or vice versa
• For undivided highways with cross-
section rotated about centerline

38. 38
Source: CalTrans Design Manual online,
http://www.dot.ca.gov/hq/oppd/hdm/pdf/chp0200.pdf

39. 39
Minimum Length of Tangent Runout
Lt = eNC x Lr
ed
where
• eNC = normal cross slope rate (%)
• ed = design superelevation rate
• Lr = minimum length of superelevation
runoff (ft)
(Result is the edge slope is same as for
Runoff segment)

40. 40
Length of Superelevation
Runoff
α = multilane adjustment factor
Adjusts for total width
r

41. 41
Minimum Length of Runoff
for curve
• Lr based on drainage and
aesthetics and design speed.
• Relative gradient is the rate of
transition of edge line from NC
to full superelevation
traditionally taken at 0.5% ( 1
foot rise per 200 feet along the
road)

42. 42
Design Requirements for
Runoffs
Maximum Relative Gradient
Relative gradient is the rate of transition of edge line from
NC to full super elevation
Relative gradient

43. 43
Relative Gradient (G)
• Maximum longitudinal slope
• Depends on design speed, higher
speed = gentler slope. For example:
• For 15 mph, G = 0.78%
• For 80 mph, G = 0.35%
• See table, next page

44. 44
Maximum Relative
Gradient (G)
Source: A Policy on Geometric Design of
Highways and Streets (The Green Book).
Washington, DC. American Association of
State Highway and Transportation Officials,
2001 4th
Ed.

45. 45
Multilane Adjustment factor
• Runout and runoff must be adjusted for
multilane rotation.

46. 46
Length of Superelevation
Runoff Example
For a 4-lane divided highway with cross-
section rotated about centerline, design
superelevation rate = 4%. Design speed
is 50 mph. What is the minimum length
of superelevation runoff (ft)
Lr = 12eα
G
•

47. 47
Lr = 12eα = (12) (0.04) (1.5)
G 0.5
Lr = 144 feet

48. 48
Tangent runout length
Example continued
• Lt = (eNC / ed ) x Lr
as defined previously, if NC = 2%
Tangent runout for the example is:
LT = 2% / 4% * 144’ = 72 feet

49. 49
From previous example, speed = 50 mph, e = 4%
From chart runoff = 144 feet, same as from calculation
Source: A Policy on Geometric
Design of Highways and
Streets (The Green Book).
Washington, DC. American
Association of State Highway
and Transportation Officials,
2001 4th
Ed.

50. 50
Transition curve

51. 51
Spiral CurveSpiral Curve
TransitionsTransitions

52. 52
Source: Iowa DOT Design Manual
SPIRAL TERMINOLOGY

53. 53
Transition Curves –
Spirals (Safety)
• Provided between tangents and
circular curves or between two
circular curves
• It provides the path where radial
force gradually increased or
decreased while entering or leaving
the circular curves

54. 54
Tangent-to-Curve
Transition (Appearance)
• Improves appearance of the highways
and streets
• Provides natural path for drivers

55. 55
Tangent-to-Curve
Transition (Superelvation or curve
widening requirement)
• Accommodates distance needed to
attain super elevation
• Accommodates gradual roadway
widening

56. 56
Ideal shape of transition curve
• When rate of introduction of C.F. is
consistent
• When rate of change C. Acceleration
is consistent
• When radius of transition curve
consistently change from infinity to
radius of circular curve

57. 57
Shape of transition
curves
• Spiral (Clotoid)= mostly used
• Lemniscates (rate of change of
radius not constant)
• Cubic parabola

58. 58
Transition Curves -
Spirals
The Euler spiral (clothoid) is used. The radius at any point of
the spiral varies inversely with the distance.

59. 59
Minimum Length of Spiral
Possible Equations: When consistent C.F is considered
Larger of (1) L = 3.15 V3
RC
Where:
L = minimum length of spiral (ft)
V = speed (mph)
R = curve radius (ft)
C = rate of increase in centripetal acceleration
(ft/s3
) use 1-3 ft/s3
for highway)

60. 60
• V= 50 mph
• C = 3 ft p c. sec
• R= 929
• Ls = 141 ft

61. 61
Minimum Length of Spiral
When appearance of the highways is considered
1.Minimum- 2.Maximum Length of Spiral
Or L = (24pminR)1/2
Where:
L = minimum length of spiral (ft) = 121.1 ft
R = curve radius (ft) = 930
pmin = minimum lateral offset between the
tangent and circular curve (0.66 feet)

62. 62
Maximum Length of Spiral
• Safety problems may occur when
spiral curves are too long – drivers
underestimate sharpness of
approaching curve (driver
expectancy)

63. 63
Maximum Length of Spiral
L = (24pmaxR)1/2
Where:
L = maximum length of spiral (ft) = 271
R = curve radius (ft)
pmax = maximum lateral offset between the
tangent and circular curve (3.3 feet)

64. 64
Length of Spiral
o AASHTO also provides recommended spiral
lengths based on driver behavior rather
than a specific equation.
o Super elevation runoff length is set equal
to the spiral curve length when spirals are
used.
o Design Note: For construction purposes,
round your designs to a reasonable values;
e.g.
Ls = 141 feet, round it to
Ls = 150 feet.

65. 65
Location of Runouts and
Runoffs
• Tangent runout proceeds a spiral
• Superelevation runoff = Spiral curve

66. 66

67. 67Source: Iowa DOT
Design Manual

68. 68Source: Iowa DOT
Design Manual

69. 69Source: Iowa
DOT Design
Manual

70. 70
Source: Iowa DOT Design Manual
SPIRAL TERMINOLOGY

71. 71
Attainment of superelevation
on spiral curves
See sketches that follow:
Normal Crown (DOT – pt A)
1. Tangent Runout (sometimes known as crown
runoff): removal of adverse crown (DOT – A to B)
B = TS
2. Point of reversal of crown (DOT – C) note A to B =
B to C
3. Length of Runoff: length from adverse crown
removed to full superelevated (DOT – B to D), D =
SC
4. Fully superelevate remainder of curve and then
reverse the process at the CS.

72. 72
Source: Iowa DOT Standard Road Plans RP-2
With Spirals
Same as point E of GB

73. 73
With Spirals
Tangent runout (A to B)

74. 74
With Spirals
Removal of crown

75. 75
With Spirals
Transition of
superelevation
Full superelevation

76. 76

77. 77
Transition Example
Given:
• PI @ station 245+74.24
• D = 4º (R = 1,432.4 ft)
∀∆ = 55.417º
• L = 1385.42 ft

78. 78
With no spiral …
• T = 752.30 ft
• PC = PI – T = 238 +21.94

79. 79
For:
• Design Speed = 50 mph
• superelevation = 0.04
• normal crown = 0.02
Runoff length was found to be 144’
Tangent runout length =
0.02/ 0.04 * 144 = 72 ft.

80. 80
Where to start transition for superelevation?
Using 2/3 of Lr on tangent, 1/3 on curve for
superelevation runoff:
Distance before PC = Lt + 2/3 Lr
=72 +2/3 (144) = 168
Start removing crown at:
PC station – 168’ = 238+21.94 - 168.00 =
Station = 236+ 53.94

81. 81
Location Example – with spiral
• Speed, e and NC as before and
∀∆ = 55.417º
• PI @ Station 245+74.24
• R = 1,432.4’
• Lr was 144’, so set Ls = 150’

82. 82
Location Example – with spiral
See Iowa DOT design manual for more
equations:
http://www.dot.state.ia.us/design/00_toc.htm#Ch
• Spiral angle Θs = Ls * D /200 = 3 degrees
• P = 0.65 (calculated)
• Ts = (R + p ) tan (delta /2) + k = 827.63 ft

83. 83
• TS station = PI – Ts
= 245+74.24 – 8 + 27.63
= 237+46.61
Runoff length = length of spiral
Tangent runout length = Lt = (eNC / ed ) x Lr
= 2% / 4% * 150’ = 75’
Therefore: Transition from Normal crown begins
at (237+46.61) – (0+75.00) = 236+71.61
Location Example – with spiral

84. 84
With spirals, the central angle for the
circular curve is reduced by 2 * Θs
Lc = ((delta – 2 * Θs) / D) * 100
Lc = (55.417-2*3)/4)*100 = 1235.42 ft
Total length of curves = Lc +2 * Ls = 1535.42
Verify that this is exactly 1 spiral length
longer than when spirals are not used
(extra credit for who can tell me why,
provide a one-page memo by Monday)
Location Example – with spiral

85. 85
Also note that the tangent length with
a spiral should be longer than the
non-spiraled curve by approximately ½
of the spiral length used. (good check
– but why???)
Location Example – with spiral

86. 86
Notes – Iowa DOT

87. 87
Quiz Answers
What can be done to improve the safety of a
horizontal curve?
 Make it less sharp
 Widen lanes and shoulders on curve
 Add spiral transitions
 Increase superelevation

88. 88
Quiz Answers
5. Increase clear zone
6. Improve horizontal and vertical
alignment
7. Assure adequate surface drainage
8. Increase skid resistance on downgrade
curves

89. 89
Some of Your Answers
 Decrease posted speed
 Add rumble strips
 Bigger or better signs
 Guardrail
 Better lane markers
 Sight distance
 Decrease radius