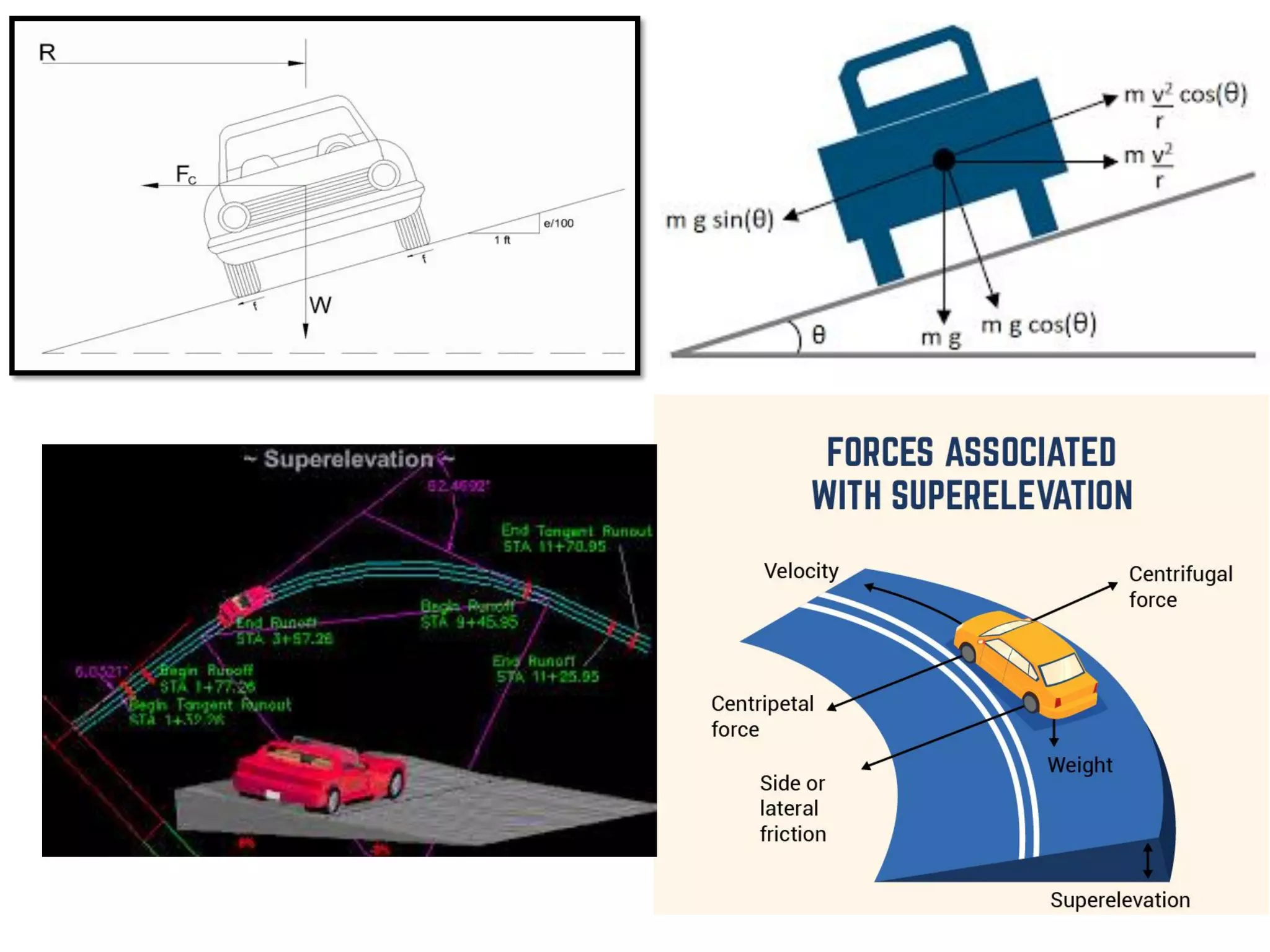
The document discusses key considerations for designing horizontal curves, including: 1. Calculating the minimum radius based on design speed, superelevation rate, and side friction factor. 2. Establishing practical maximum limits for superelevation rate of 8-12% due to factors like snow, driver comfort. 3. Using transition curves to gradually develop superelevation over a length determined by design speed and superelevation rate. 4. Widening the carriageway on curves below a certain radius to allow vehicles to pass safely. Iterative design is recommended to consider factors like cost, sight distance, and aesthetics beyond minimum standards.

1. HORIZONTAL ALIGNMENT

2. Horizontal Alignment
The key steps in the design of horizontal curves are
listed below.
• Determine a reasonable maximum superelevation
rate
• Decide upon a maximum side-friction factor
• Calculate the minimum radius for your horizontal
curve
• Iterate and test several different radii until you are
satisfied with your design
• Make sure that the stopping sight distance is
provided throughout the length of your curve.
Adjust your design if necessary.
• Design the transition segments

3. Superelevation and Side-Friction
• Most highways will change directions several
times over the course of their lengths.
• These changes may be in a horizontal plane, in
a vertical plane, or in both
• The superelevation of the highway
cross-section and the side-friction factor are
two of the most crucial components in the
design of horizontal curves.

6. Superelevation and Side-Friction
• The superelevation is normally discussed in
terms of the superelevation rate, which is the
rise in the roadway surface elevation as you
move from the inside to the outside edge of the
road
• For example, a superelevation rate of 10%
implies that the roadway surface elevation
increases by 1 ft for every 10 ft of roadway
width.
• The side-friction factor is simply the coefficient
of friction between the design vehicle's tires and
the roadway.

7. General Considerations
• From accumulated research and experience,
limiting values for superelevation rate (emax
) and
side friction
• demand ( fmax
) have been established for curve
design.
• Using these established limiting values in the
basic curve formula permits determining a
minimum curve radius for various design
speeds.

8. General Considerations
• Use of curves with radii larger than this
minimum allows superelevation, side friction,
or both to have values below their respective
limits.
• The amount by which each factor is below its
respective limit is chosen to provide an
equitable contribution of each factor toward
sustaining the resultant lateral acceleration.

9. Superelevation
• There are practical upper limits to the rate of
super elevation on a horizontal curve.
• These limits relate to considerations of climate,
constructability, adjacent land use, and the
frequency of slow-moving vehicles.
• Where snow and ice are a factor, the rate of
superelevation should not exceed the rate on
which vehicles standing or traveling slowly
would slide toward the center of the curve when
the pavement is icy.
•

10. Superelevation
• At higher speeds, the phenomenon of partial
hydroplaning can occur on curves with poor
drainage that allows water to build up on the
pavement surface.
• Skidding occurs, usually at the rear wheels, when
the lubricating effect of the water film reduces
the available lateral friction below the friction
demand for cornering.

11. Superelevation
• When travelling slowly around a curve with
high superelevation, negative lateral forces
develop and the vehicleis held in the proper
path only when the driver steers up the slope
or against the direction of the horizontal curve
• Some vehicles have high centers of gravity and
some passenger cars are loosely suspended on
their axles
• When these vehicles travel slowly on steep
cross slopes, the down-slope tires carry a high
percentage of the vehicle weight

12. Superelevation
• There are practical maximum limits for the rate
of superelevation.
• In areas where ice and snow are expected, a
superelevation rate of 8% seems to be a
conservative maximum value.
• In areas that are not plagued by ice and snow, a
maximum superelevation rate of 10-12% seems
to be a practical limit.
• Both modern construction techniques and driver
comfort limit the maximum superelevation rate
to 12%.

13. Geometric Design Guide of RHD

14. Side Friction Factor
• The side friction factor represents the
vehicle’s need for side friction, also called the
side friction demand; it also represents the
lateral acceleration af
that acts on the vehicle.
• In every case, the side-friction factor that is
used in design should be well below the
side-friction factor of impending release.

15. Side Friction Factor
• In addition to the safety concerns, drivers
don't feel comfortable if the roadway seems to
rely heavily on the frictional force.
• The side-friction factors that are employed in
the design of horizontal curves should
accommodate the safety and comfort of the
intended user

16. Side Friction, Superelevation , Radius and Velocity

17. Side Friction Factor Recommended by AASHTO (2011) for
Horizontal Curve

18. Side Friction Factor Recommended by AASHTO (2011) for
Horizontal Curve

19. Minimum Radius Calculations
Calculating the minimum radius for a horizontal
curve is based on three factors:
• the design speed,
• the superelevation, and
• the side-friction factor
The minimum radius serves not only as a constraint
on the geometric design of the roadway, but also as
a starting point from which a more refined curve
design can be produced.

20. Minimum Radius Calculations
• For a given speed, the curve with the smallest
radius is also the curve that requires the most
centripetal force.
• The maximum achievable centripetal force is
obtained when the superelevation rate of the
road is at its maximum practical value, and the
side-friction factor is at its maximum value as
well.
• Any increase in the radius of the curve beyond
this minimum radius will allow you to reduce
the side-friction factor, the superelevation rate,
or both.

21. Minimum Radius of Curvature
This equation allows the engineer to calculate the
minimum radius for a horizontal curve based on the
design speed, the superelevation rate, and the side
friction factor.

22. Design Iterations for Curve Radius
• In many ways, horizontal alignment is an art form.
• The goal is to produce a horizontal curve that is
comfortable and safe to use, and also cost
efficient and aesthetically pleasing.
• The first step is to calculate the radius of the
horizontal curve.
• We can calculate the radius for any combination
of superelevation and side-friction factors using
the equation mentioned before.

23. Design Iterations for Curve Radius
• As long as the radius of your curve is above
the minimum radius as described in the
minimum radius module, and as long as you
haven't exceeded the practical values for the
superelevation or for the side-friction factor,
you know that your design is acceptable .

24. Design Iterations for Curve Radius
• You will probably need to test several different
curve radii before you select your final design.
• While iterating, you also need to consider
other factors:
– the cost, environmental impacts, sight distances,
and, of course, the aesthetic consequences of your
curve.

25. Example
• A new transportation engineer is assigned with
the design of a horizontal curve for A
Highway. His final design decides for a curve
with a radius of 520 meters. Verify his design.
• Assume that the design speed for the highway
is 110 km/h
• You can also assume that snow and ice will be
present on the roadway from time to time.

26. Solution
• The first step in a review of his plans would be to
make sure that the curve radius as designed is
greater than the minimum curve radius. For a
design speed of 110 km/h, the comfortable
side-friction factor is 0.10.
• In addition, since the roadway will be covered
with snow and ice from time to time, the
maximum superelevation rate is 8%.

27. Solution
With this information we can go ahead and calculate the
minimum curve radius using the equation below.
• Rmin
= V2
/(127(e max
/100 +fmax
))
• Where:
Rmin
= Minimum radius (m)
V = Design speed,110 km/hr
emax
= Maximum superelevation rate, 8%
fmax
= Maximum side-friction factor, 0.10
• Substituting and solving yields a minimum radius of 530
meters.
• The 520 meter radius that is called for in the plans would
probably work, but it might be uncomfortable for the
vehicle occupants. A larger radius would be appropriate.

28. Horizontal Alignment
(RHD Design Guide)
• The horizontal alignment of single carriageway roads
will normally consist of a series of straights (tangents)
or very large radius curves, linked by smaller radius
curves.
• Continuous curving alignments with few or no straight
sections are not recommended, because unless the
curve radii are very large they will not provide
sufficient sight distance to allow drivers to clearly see
whether it is safe to overtake.
• Instead, relatively short curves, at or near the
minimum radius for the design speed should be used
in conjunction with straights or very large radius
curves.

31. Horizontal Alignment
(RHD Design Guide)
• Maximising safe overtaking conditions is one
of the key objectives of alignment design.
• This is especially important in Bangladesh
where there is a large proportion of
slow-moving vehicles Excessive lengths of
straight should be avoided as these could
encourage dangerously high speeds.
• Very large radius curves (>5000m radius) are
safer than long straight sections.

32. Horizontal Alignment
(RHD Design Guide)
• A succession of curves and straights makes for a
more interesting driving task, and helps the driver
stay in control.
• Drivers are better able to assess the distances and
speeds of other vehicles, they are more likely to
remain alert, and there is less headlight glare at
night.
• Continuous curving alignments are more
acceptable on dual carriageway roads because
there is no need to provide overtaking sight
distance.

33. Determining the Curve Parameters
(RHD Design Guide)
The key design parameter for circular curves is the radius,
and the main factors that help determine the appropriate
value are the design speed and the required sight distance.
A step by step guide to determining curve radius and
related design parameters is given below:
1. Decide what sight distance to use
• The Intermediate Sight Distance (ISD) provides a good
starting point for curve design.
• It avoids the need for superelevation and makes future
upgrades much easier.
• Single lane roads and dual carriageway roads must always
be designed to provide Intermediate Sight Distance.

34. Determining the Curve Parameters
(RHD Design Guide)
2.Use Table 5.1 to determine the minimum curve radius
• Knowing the road type and the design speed, and
having selected a sight distance, read off the
appropriate value for curve radius.
3. Check for feasibility – amend if necessary
• If site constraints prevent a curve of this radius being
provided, check whether a curve to Stopping Sight
Distance (SSD) requirements will be feasible.
• Do not use curves whose radius is between the ISD and
SSD standards as these could tempt drivers to overtake
when there is not enough visibility – curves must be
clearly non-overtaking (SSD standards) or clearly
overtaking (at least ISD standards and preferably
Overtaking Sight Distance standards).

35. Determining the Curve Parameters
(RHD Design Guide)
4. Use Table 5.2 to determine the minimum
superelevation requirements
• Knowing the design speed and the curve radius
the appropriate value of superelevation is read
off from Table 5.2.
• In some cases no superelevation will be
required. Refer to Section 5.3.

36. Determining the Curve Parameters
(RHD Design Guide)
5. Use Table 5.3 to determine minimum transition
lengths
• Knowing the design speed and the superelevation
the appropriate transition length is read off from
Table 5.3. Refer to Section 5.4.
• If transition curves are not being used Table 5.3
can be used to find the superelevation
development length (Lp + Lc).
6. Use Table 5.4 to determine whether there are any
curve widening requirements Knowing the road type
and the curve radius the appropriate curve widening
(if any) is read off from Table 5.4. Refer to Section
5.5.

37. Determining the Curve Parameters
(RHD Design Guide)

38. Determining the Curve Parameters
(RHD Design Guide)

39. Determining the Curve Parameters
(RHD Design Guide)

41. Transition Curves
• The length of the transition curve is dependent
on the superelevation requirements.
• The transition curve is used to develop the
superelevation from where the outer lane is level
to full superelevation at the start of the circular
curve – see Figure 5.1.
• Table 5.3 gives the minimum lengths to be used.
It is desirable to use a transition curve length that
is one design speed and one superelevation value
higher than indicated by the input values in order
to allow for future road upgrades

42. Figure 5.1 Development of Superelevation on Transitioned
Curves
S.LC = Start of
superelevation
development
TS = Tangent to
spiral point
SC = Spiral to curve
point

45. Curve Widening
• It is necessary to widen the carriageway on small radius
curves in order to enable vehicles to pass each other
safely.
• The lateral positioning of vehicles varies more on a curve
than on a straight.
• Moreover long vehicles occupy a greater width of
pavement on a curve.
• The amount of widening needed is dependent on the
curve radius, the width of the carriageway, and the type of
the vehicle.
• Table 5.4 sets out the extra carriageway widths that are
required.
• These are appropriate for rigid two-axle vehicles similar to
the buses and trucks widely used in Bangladesh.

47. Curve Widening

48. Compound Curve
Reverse Curve
• Compound, Reverse
and are Broken back
curves are discouraged
to use unless very
unusual topography or
right of way dictate