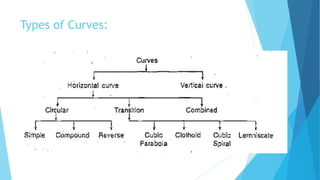
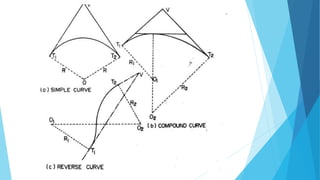
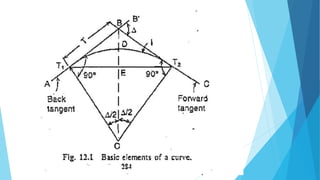
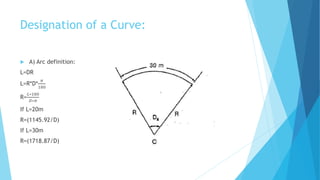
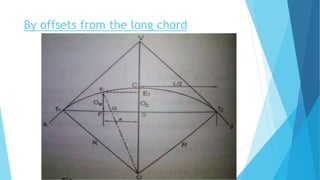
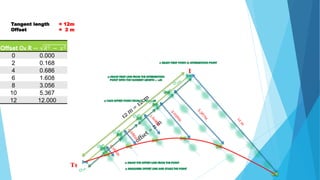
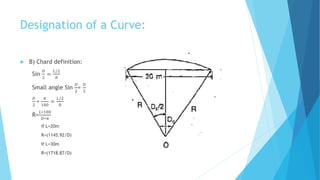
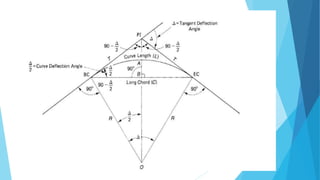
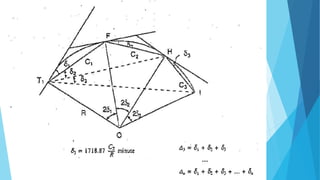
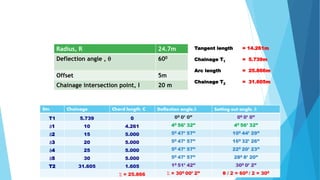
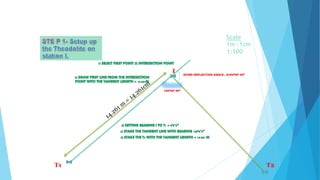
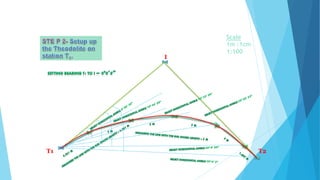
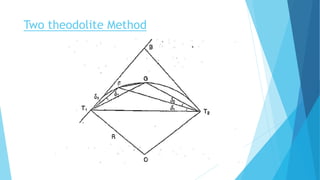
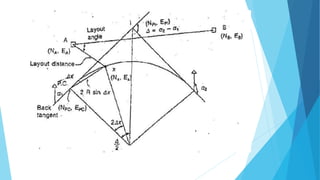
This document discusses methods for setting out simple circular curves in surveying. There are two main methods: linear and angular. The linear method uses only a tape or chain and does not require angle measurement. It includes setting out curves by offsets from the long chord, by successive bisection of arcs, and by offsets from the tangents. The angular method is used for longer curves and involves measuring deflection angles. It includes Rankine's method of tangential angles using a tape and theodolite to measure deflection angles from the back tangent to points on the curve. The two theodolite method also uses angle measurement between two theodolites.

1. SURVEYING
Simple Circular Curves
Presented By
Srikanth Samudrala
Department of CIVIL ENGINEERING
KAMALA INSTITUTE OF TECHNOLOGY AND SCINCE, SINGAPUR

2. Types of Curves:

5. Designation of a Curve:
 A) Arc definition:
L=DR
L=R*D*
𝜋
180
R=
𝐿∗180
𝐷∗𝜋
If L=20m
R=(1145.92/D)
If L=30m
R=(1718.87/D)

6. Designation of a Curve:
 B) Chard definition:
Sin
𝐷
2
=
𝐿/2
𝑅
Small angle Sin
𝐷
2
=
𝐷
2
𝐷
2
∗
𝜋
180
=
𝐿/2
𝑅
R=
𝐿∗180
𝐷∗𝜋
If L=20m
R=(1145.92/D)
If L=30m
R=(1718.87/D)

7. Circular Curve Geometry

11. Based on the instruments used in setting out the curves on the ground there are
two methods:
1) Linear method
2) Angular method
Methods of setting out simple
circular curve

12. Linear Method
 In these methods only tape or chain is used for setting out the curve . Angle
measuring instrument are not used.
Main linear methods are
 By offsets from the long chord.
 By successive bisection of arcs.
 By offsets from the tangents.

13. By offsets from the long chord

14. R = Radius of the curve
0o = Mid ordinate
0x = ordinate at distance x from the mid point
of the chord
T1 and T2 = Tangent point
0o = R -- 𝑅2 − (
𝐿
2
)2
0x = (𝑅2 −𝑥2 ) –(R – 0o)

15. Offset,
0x
(𝑅2 −𝑥2 ) –
(R – 0o)
0 3.515
2 3.347
4 2.828
6 1.907
8 0.459
8.485 0.000
Long chord length = 16.971
L/2 = 8.845m
Offset interval = 2 m
Scale
1m :1cm
1:100
W = 16.971 m
T1 T2
W/2 = 8.845m W/2 = 8.845m
2 m 2 m 2 m 2 m 0.459 m
O0m O2m O4m O6m O8m O8.845mO2mO4mO6mO8mO8.845m
3.515m
3.515m
2.828m
1.907m
2.828m
3.515m
2.828m
1.907m
2.828m

16. By successive bisection of arcs

17.  Join the tangent points T1,T2 and bisect the long chord at D.
 Erect perpendicular DC at D equal to the mid ordinate.
 Join T1C and T2C and bisect them at D1 and D2 respectively.
 D1 & D@ set out perpendicular offsets C1D1=C2D2=(1- cos
∆
4
) and obtain points
C1 and C2 on the curve.

18. By offsets from the tangents
 The offsets from the tangents can be of two types
1) Radial offsets
2) Perpendicular offsets

19. 1) Radial offsets
 0X = 𝑅2 + 𝑥2 -- R

20. 2) Perpendicular offsets
 Ox = R -- 𝑅2 − 𝑥2

21. Offset Ox R -- 𝑅2 − 𝑥2
0 0.000
2 0.168
4 0.686
6 1.608
8 3.056
10 5.367
12 12.000
Tangent length = 12m
Offset = 2 m
I
T1

22. Angular Method
 This methods are used when the length of curve is large.
The Angular methods are:
1) Rankine method of tangential angles
2) Two theodolite method
3) Tacheometric method

23. Rankine method of tangential angles
 this method also known as Tape and Theodolite method
 “A deflection angle to any point on the curve is the angle at p.c. between the
back tangent and the chord from p.c. to that point.”

25. Radius, R 24.7m
Deflection angle , q 600
Offset 5m
Chainage intersection point, I 20 m
Tangent length = 14.261m
Chainage T1 = 5.739m
Arc length = 25.866m
Chainage T2 = 31.605m
Stn. Chainage Chord length, C Deflection angle, Setting out angle, 
T1 5.739 0 00 0’ 0” 00 0’ 0”
1 10 4.261 40 56’ 32” 40 56’ 32”
2 15 5.000 50 47’ 57” 100 44’ 29”
3 20 5.000 50 47’ 57” 160 32’ 26”
4 25 5.000 50 47’ 57” 220 20’ 23”
5 30 5.000 50 47’ 57” 280 8’ 20”
T2 31.605 1.605 10 51’ 42” 300 0’ 2”
 = 25.866  = 300 00’ 2” θ / 2 = 600 / 2 = 300

26. I
T1
Scale
1m :1cm
1:100
T2
120000’ 00”
GIVEN DEFLECTION ANGLE , θ=60000’ 00”

27. I
T1
Scale
1m :1cm
1:100
T2

28. Two theodolite Method