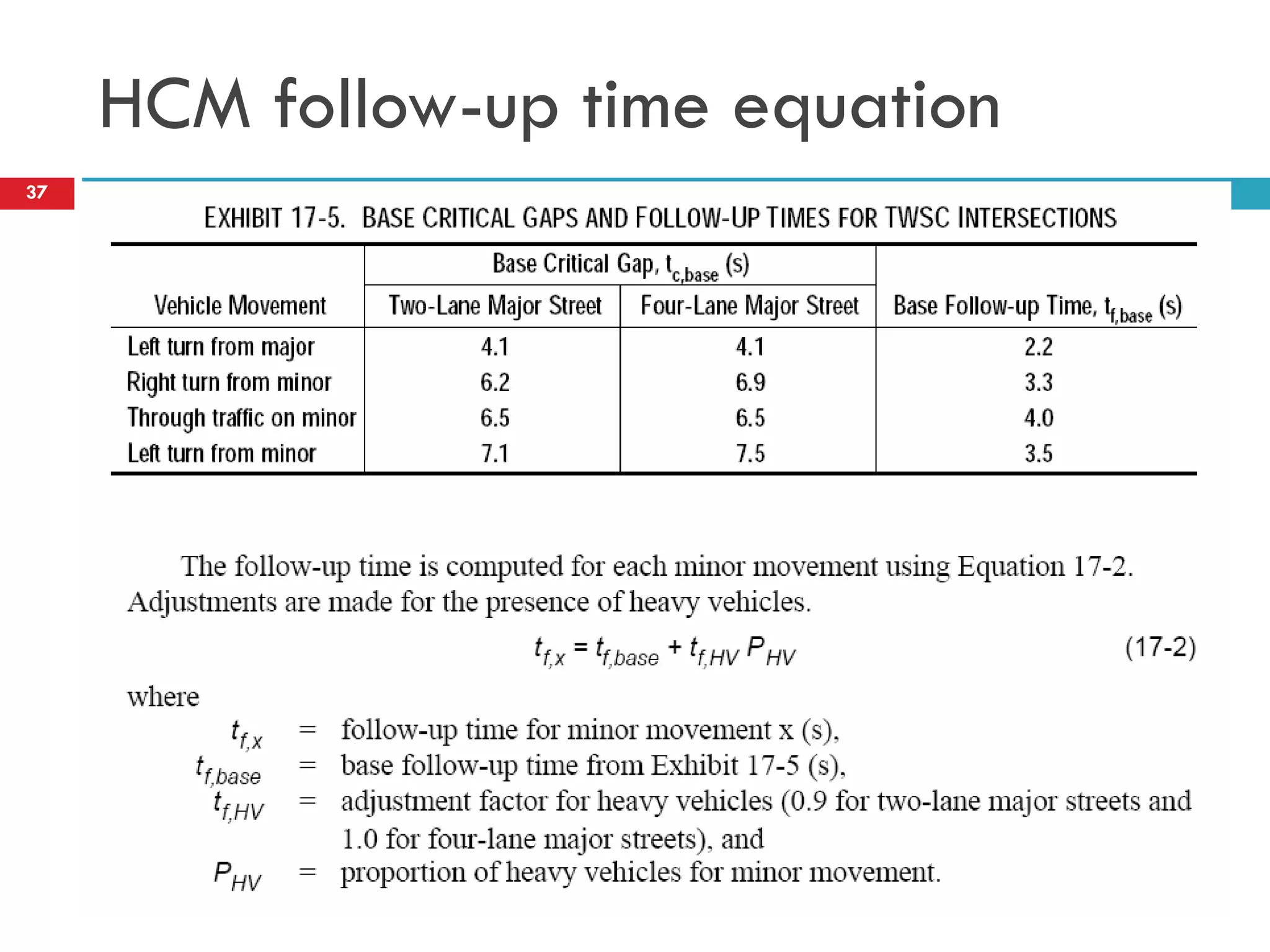
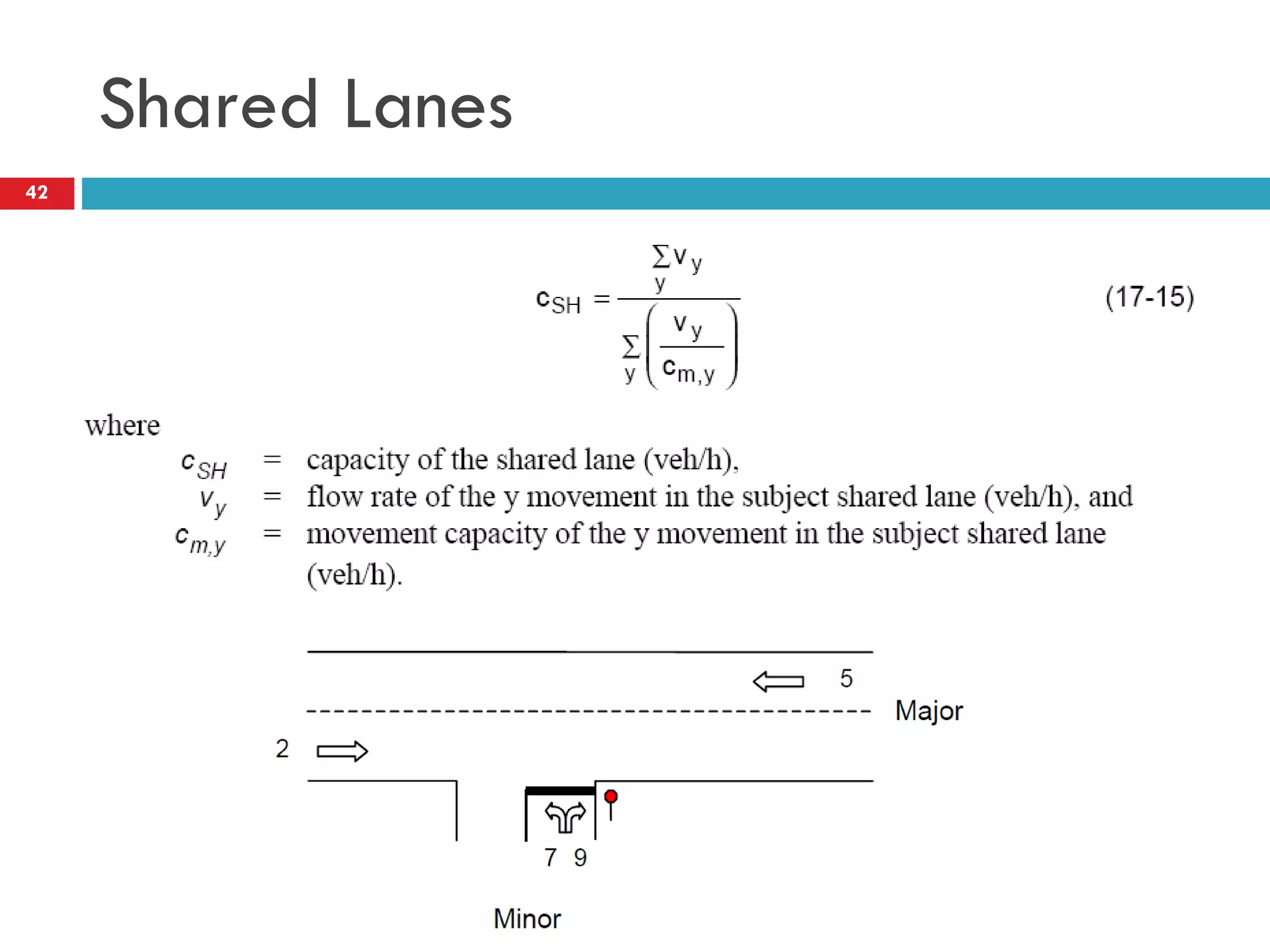
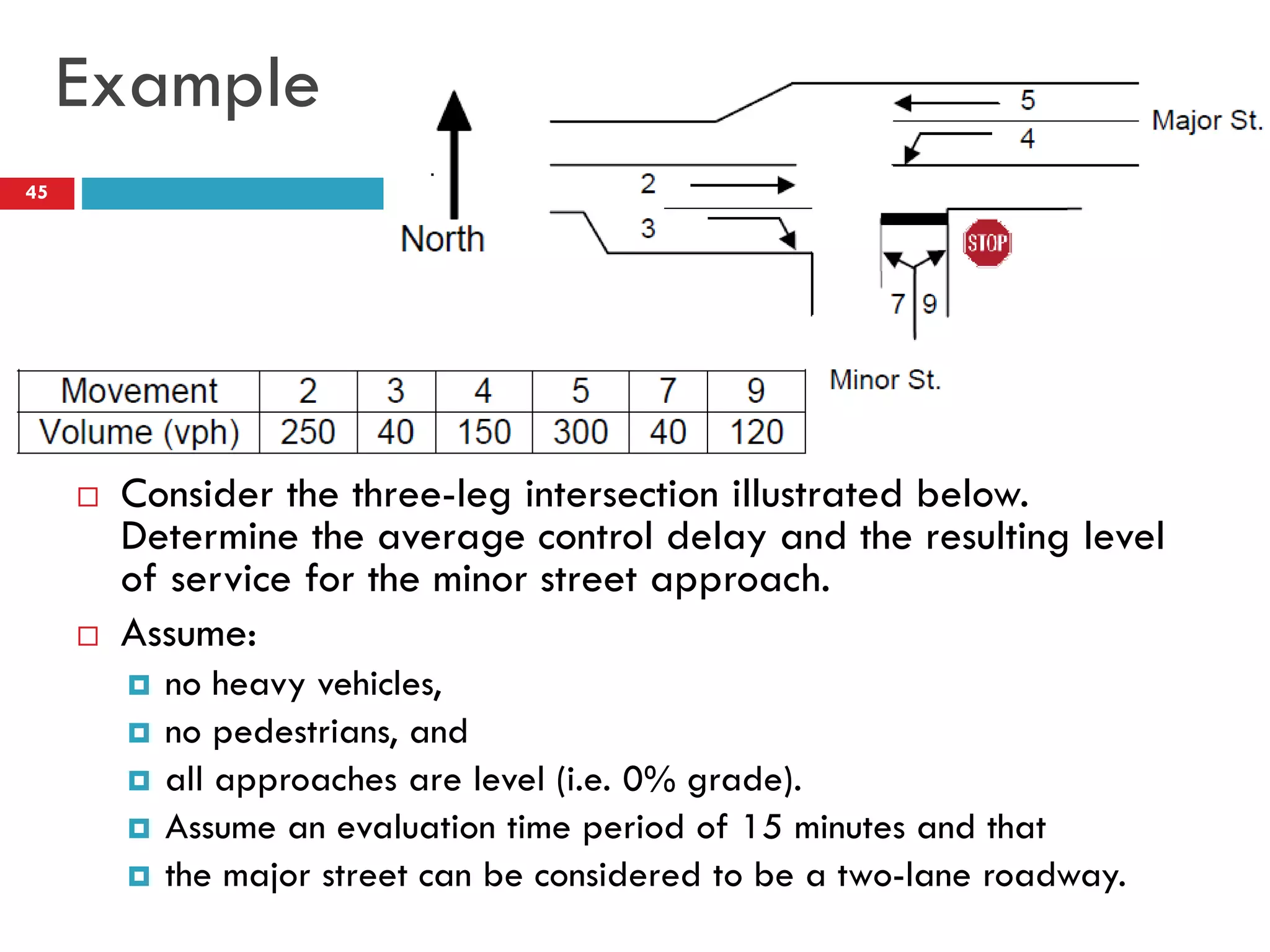
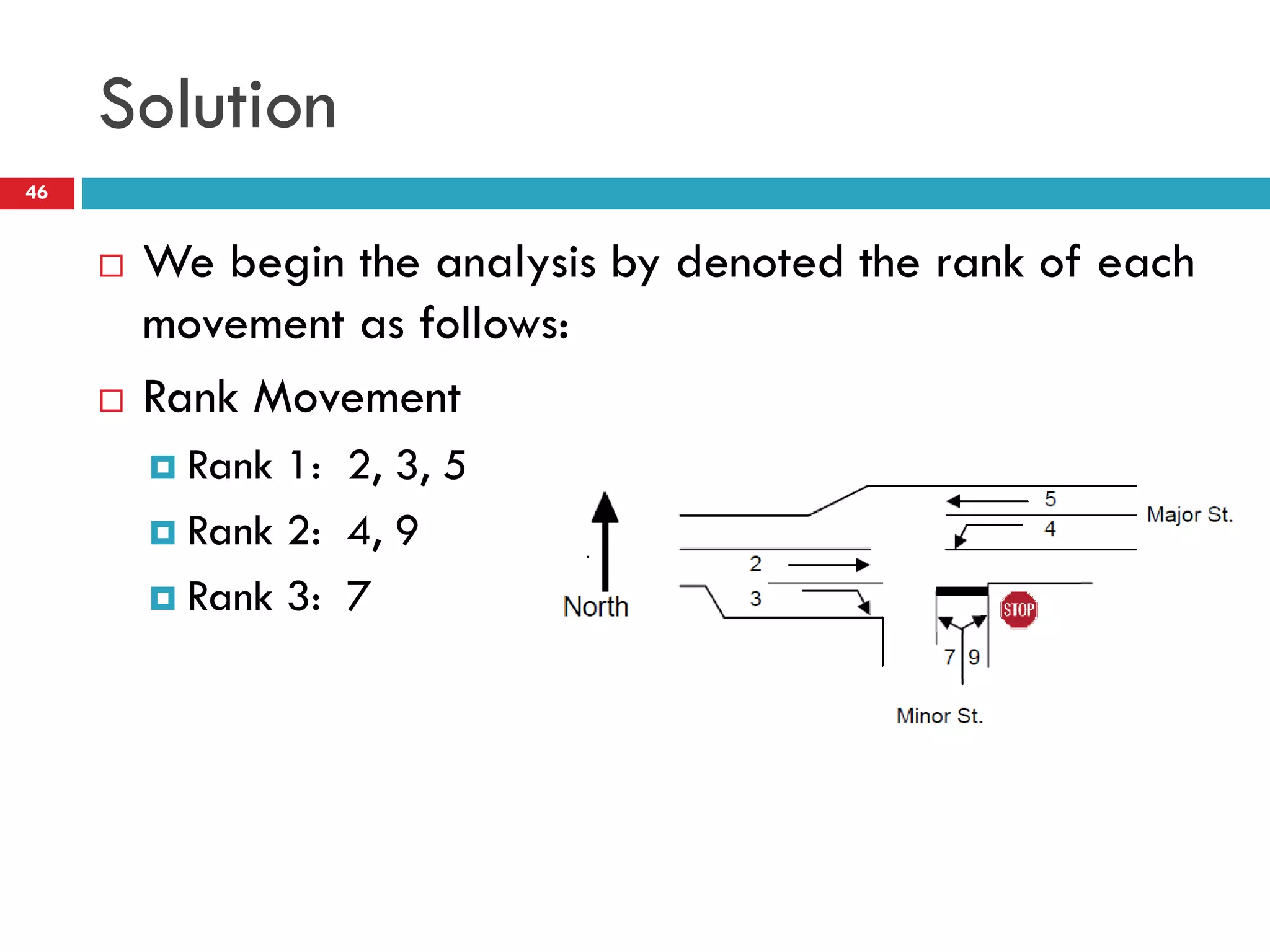
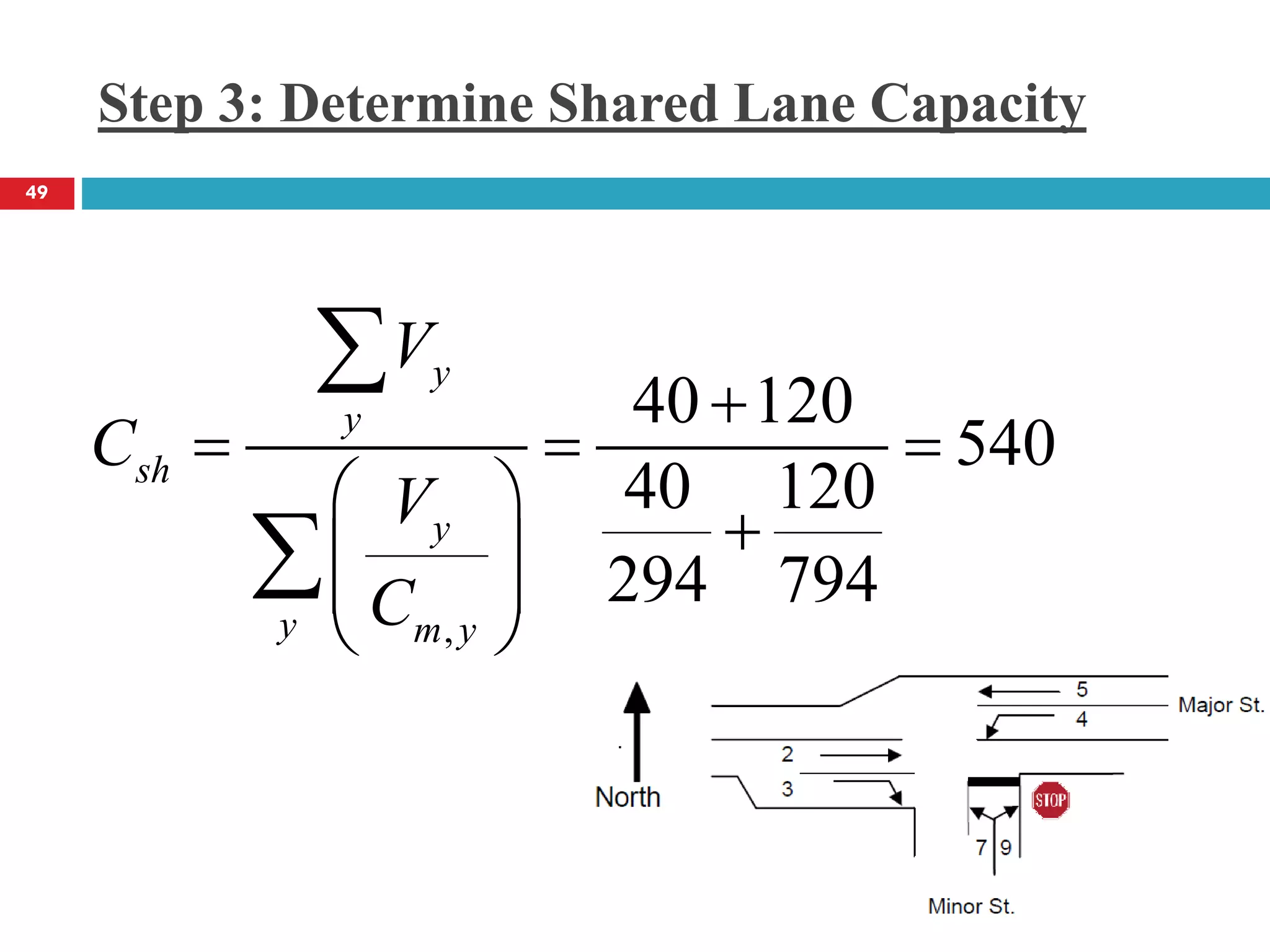
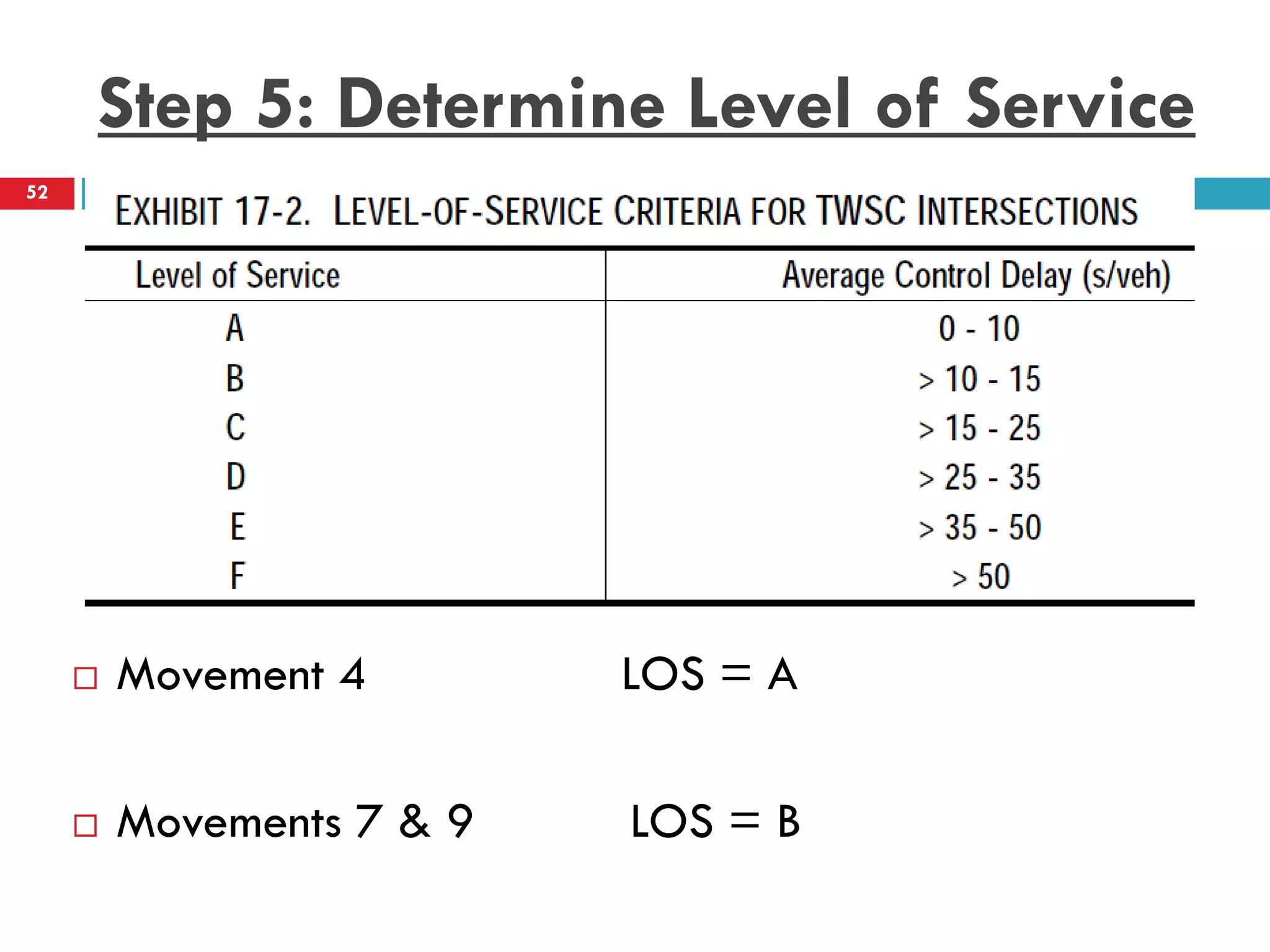
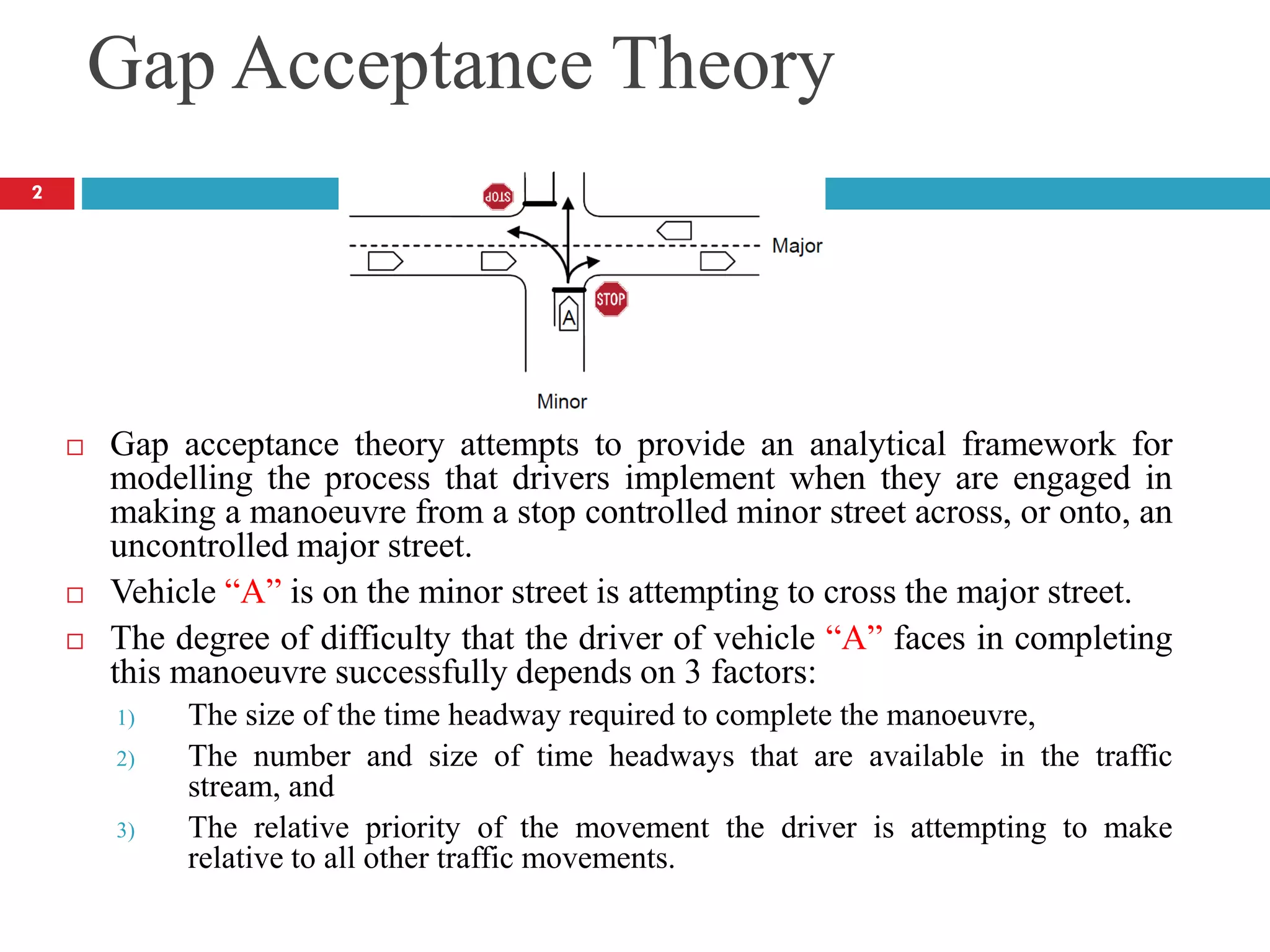
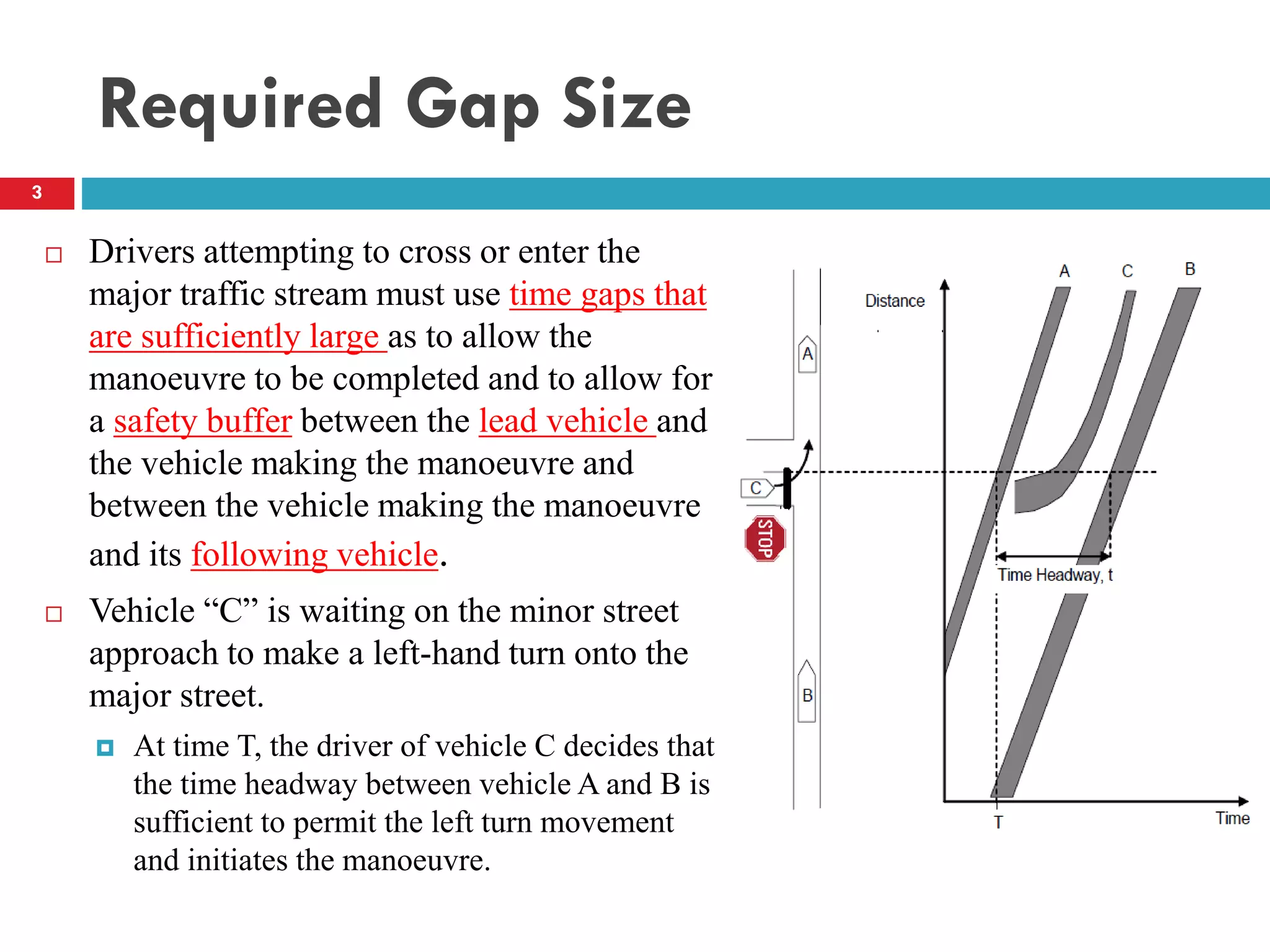
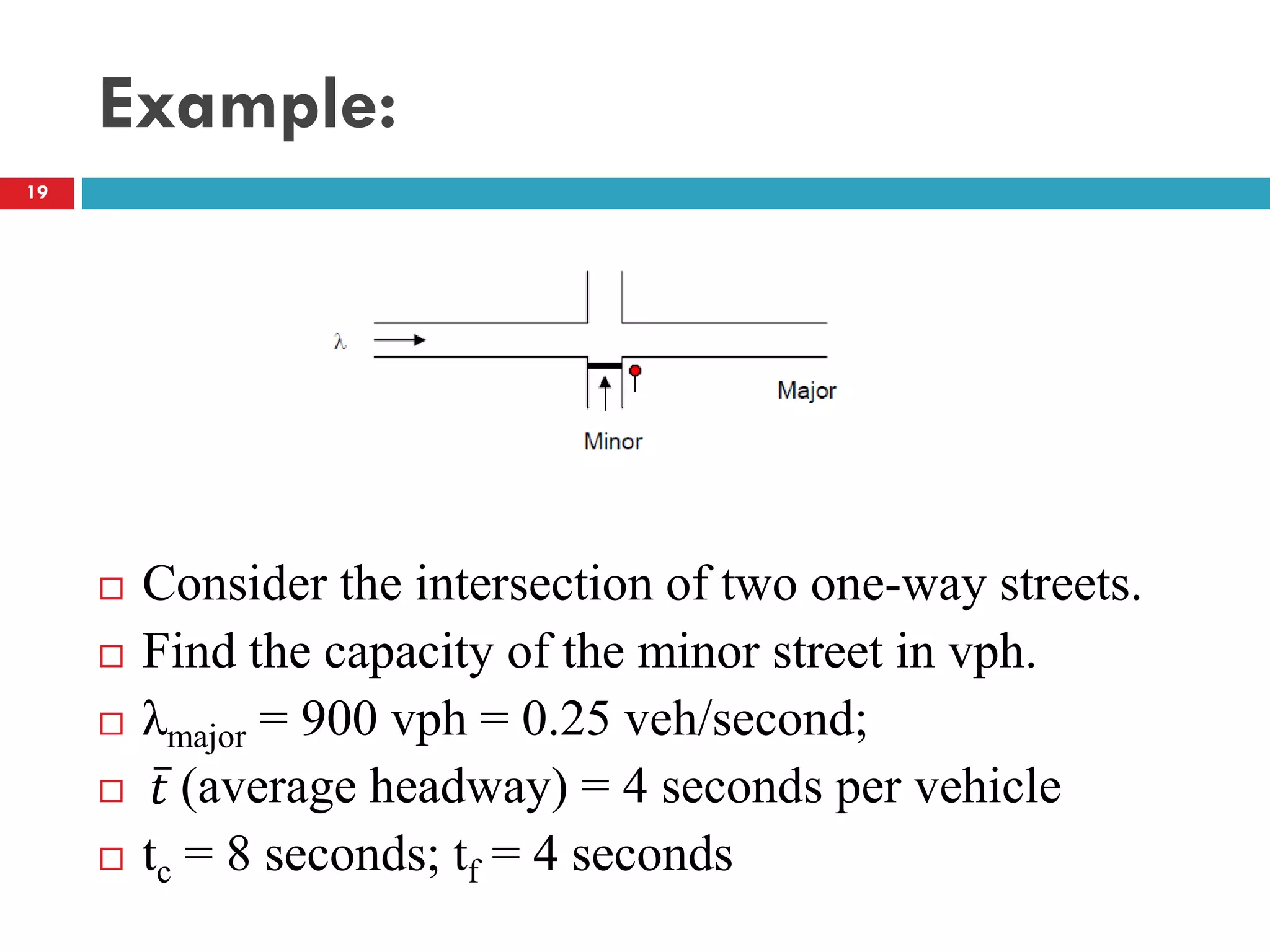
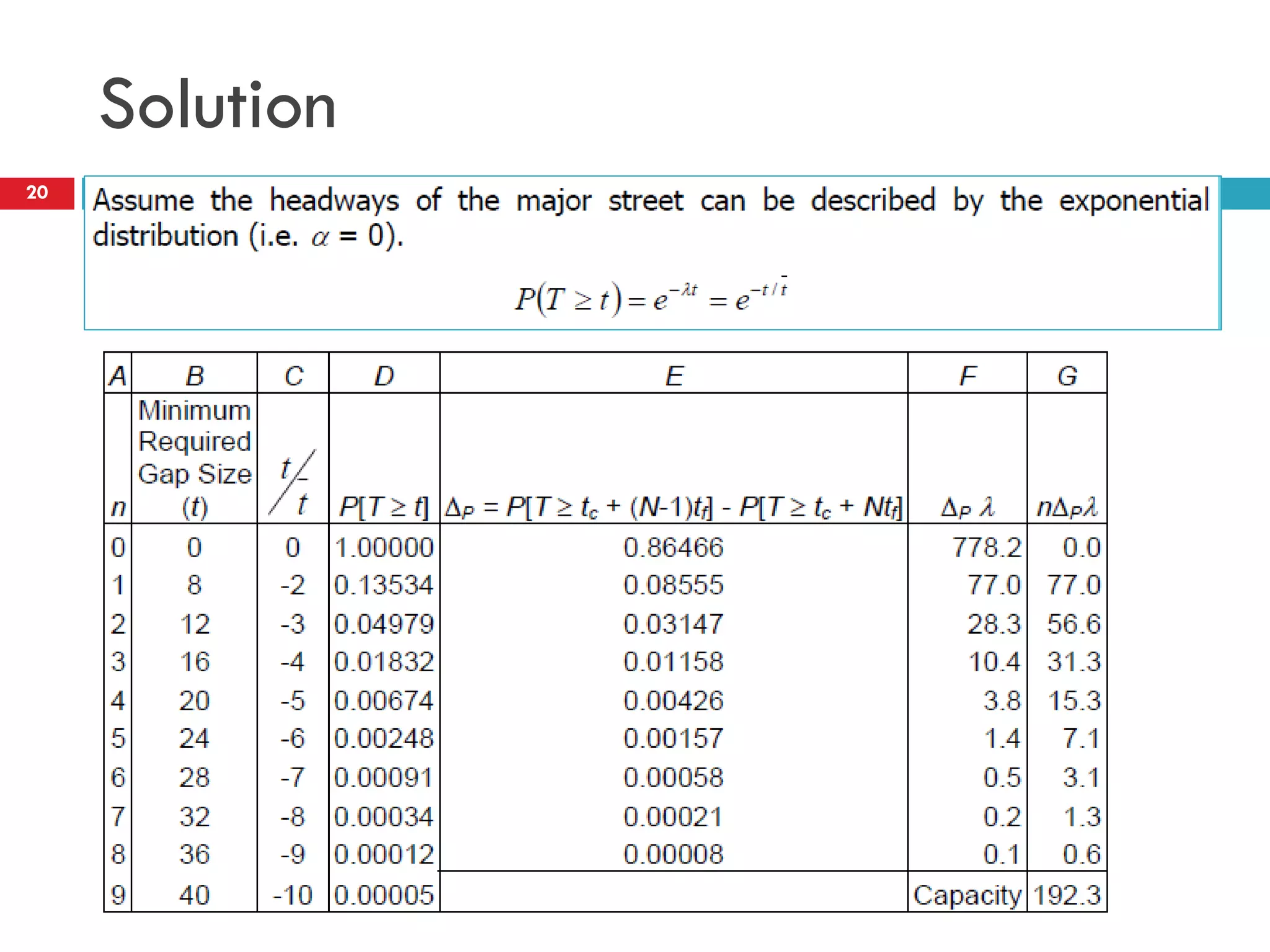
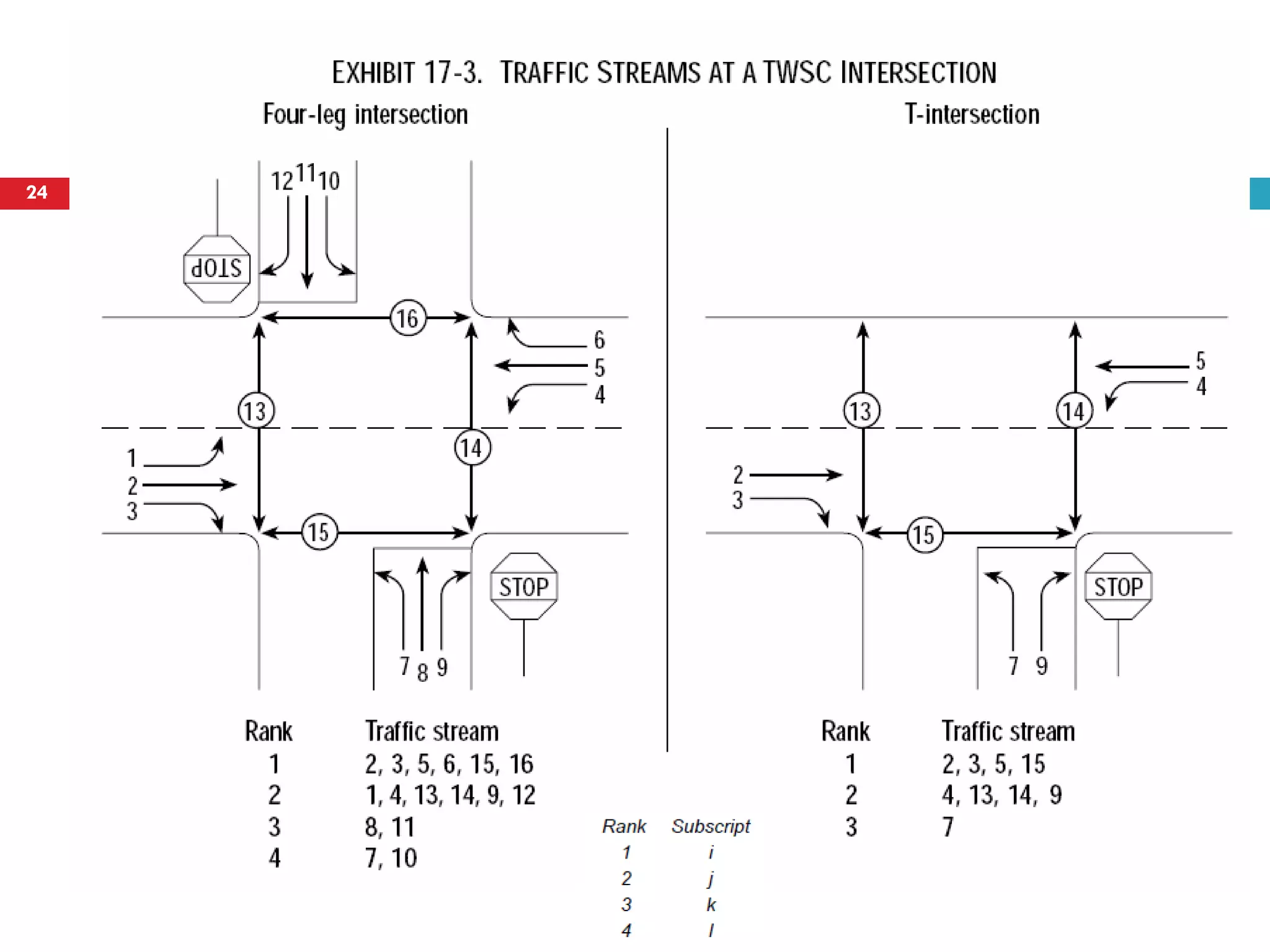
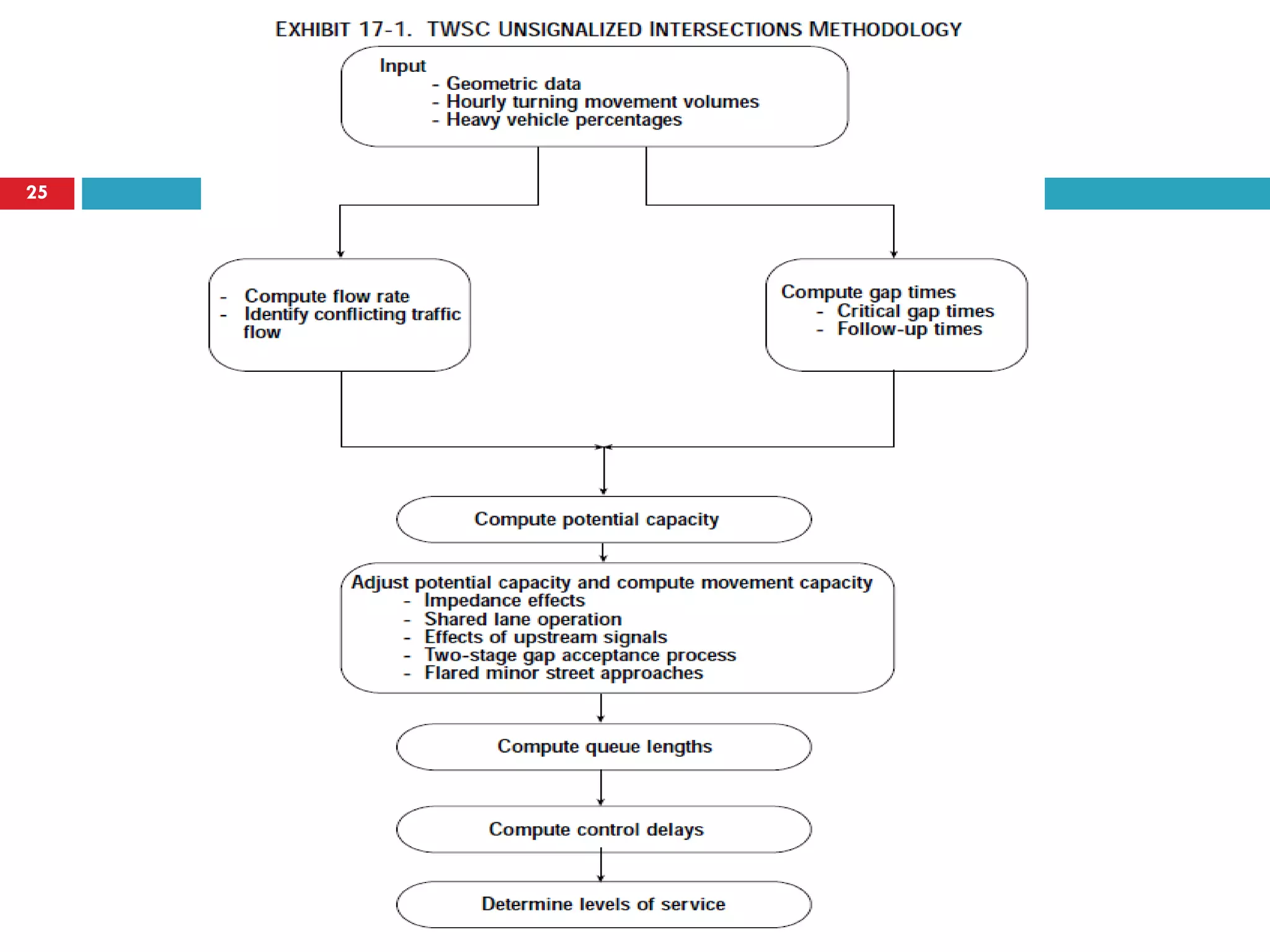
This document discusses gap acceptance theory and its application in determining the capacity of traffic movements at two-way stop controlled (TWSC) intersections. It covers key concepts such as critical gap (tc), follow-up time (tf), and impedance. An example calculation is provided to estimate capacity for different movements based on conflicting traffic volumes and tc/tf values. Adjustments to tc and tf for factors like vehicle type and number of lanes are also outlined. Finally, the document provides the Highway Capacity Manual (HCM) methodology for calculating control delay and level of service at TWSC intersections.

1. TRAFFIC ENGINEERING COURSE
(PWE 8322)
CAPACITY FOR TWSC
Instructor: Usama Elrawy Shahdah, PhDLecture # 04

2. Gap Acceptance Theory
 Gap acceptance theory attempts to provide an analytical framework for
modelling the process that drivers implement when they are engaged in
making a manoeuvre from a stop controlled minor street across, or onto, an
uncontrolled major street.
 Vehicle “A” is on the minor street is attempting to cross the major street.
 The degree of difficulty that the driver of vehicle “A” faces in completing
this manoeuvre successfully depends on 3 factors:
1) The size of the time headway required to complete the manoeuvre,
2) The number and size of time headways that are available in the traffic
stream, and
3) The relative priority of the movement the driver is attempting to make
relative to all other traffic movements.
2

3. Required Gap Size
 Drivers attempting to cross or enter the
major traffic stream must use time gaps that
are sufficiently large as to allow the
manoeuvre to be completed and to allow for
a safety buffer between the lead vehicle and
the vehicle making the manoeuvre and
between the vehicle making the manoeuvre
and its following vehicle.
 Vehicle “C” is waiting on the minor street
approach to make a left-hand turn onto the
major street.
 At time T, the driver of vehicle C decides that
the time headway between vehicle A and B is
sufficient to permit the left turn movement
and initiates the manoeuvre.
3

4. Required Gap Size (cont.)
The size of the time gap required to complete a manoeuvre is a function
of many parameters, including:
1) The physical length of vehicle C.
 Consider the same time headway between vehicles A and B, but in this case
vehicle C is a tractor-trailer.
 Even though the truck accelerates at the same rate as vehicle C in previous slide,
the length of the truck occupies a greater portion of the roadway and
 if vehicle B does not decelerate, there will be a collision.
2) Acceleration capabilities of vehicle C.
 A vehicle that accelerates quickly is able to clear the roadway in less time and
therefore can safely use a smaller gap than a vehicle that accelerates slowly.
3) Characteristics of the driver of vehicle C.
 A cautious driver generally requires a longer gap than a more aggressive driver.
 Some drivers are not capable of accurately estimating the gap size, and therefore
compensate by requiring longer gaps.
4) Width of the major roadway.
 The number of lanes that need to be crossed by vehicle C impacts the size of gap
required,
 as the gap must be long enough to permit the vehicle to safely clear the conflict
zone.
5) The type of manoeuvre being executed.
 left turn movement from a minor street requires a longer time gap than does a
through movement.
 For the left turn movement, vehicle C is merging with a traffic stream and must
not "cut off" the following vehicle (vehicle B ) such that a rear-end collision
results.
4

5. Usefulness of gaps
 The usefulness of gaps depends on:
 whether or not drivers from the minor street will make
use of an available gap, and
 if they do, how many drivers will complete their
manoeuvre in the same gap.
 Need to be able to answer two questions:
1) Will drivers be able to use a gap of a specific
duration (e.g. 10 seconds)?
2) If drivers are able to use the gap, How many drivers
will depart in this gap?
5

6. Capacity
 The maximum number of vehicles that can
complete one or more specific manoeuvres (e.g.
left turn) from the minor street approach during 1
hour
Note: Estimates of delay and queue length can be made on the
basis of capacity and the number of vehicles attempting to
make the manoeuvre.
6

7. Critical gap and follow-up time
 Critical gap (tc) (Critical time headway) : The minimum gap size in the
major steert that drivers in the minor street will accept.
 Follow-up time (tf):
 if the gap is long enough, then more than one vehicle will complete
their intended manoeuvre in the gap.
 The time required for each non-first vehicle to initiate its manoeuvre
and clear the stop line is referred to as the “follow-up time”
 Minimum headway between two consecutive vehicles in the minor stream
 Critical gap and follow-up time:
 varies from driver to driver and
 varies for a single driver from situation to situation.
 there exist distributions of values for tc and tf
 Using distributions complicates the determination of capacity of the minor street
approach.
7

8. Critical gap and follow-up time
 Assumptions to remove these distributions:
1) Drivers are consistent in that a driver behaves the same way each time
she is faced with the same traffic conditions (i.e. drivers do not change
behaviour with time).
2) The driver population is homogeneous in that all drivers behave in the
same way and have the same gap size requirements (i.e. there is no
distribution of driver types).
 The errors incurred by these unrealistic assumptions counteract
each other and that the resulting total error is small
 Assume that tc and tf are constants instead of distributions.
 Different constant values of tc and tf are used for :
 different minor street movements (e.g. left turn versus a through
movement).
 different vehicle types (e.g. trucks versus passenger cars)
8

9. Estimating tc and tf (using filed data)
 field data reflects a range of
time headways used by 1, 2,
3, …, n vehicles.
 Estimate the mean time gap
used by 1 vehicle, the mean
gap used by 2 vehicles, etc.
 use linear regression to find
the single value for tc and tf
that best fit the observed
data.
 Linear Relationship: n = at + b
 a: the slope of the line
 b: the intercept.
4 6 8 10 12
Gap Size (Sec)
Accepted gap by only One Vehicle
9

10.  The relationship between the number of vehicles using a gap and the gap size
is a step function.
 tf is the additional time required for another vehicle to use the same gap:
tf = 1/a
 The critical time headway is the time required for the first vehicle to use a
gap.
 Step function B reflects the assumption that the regression accounts for
variance in driver behaviour and therefore point C represents the critical gap.
 For this assumption: tc(B) = t0 + tf
 t0 = -b/a (by setting t = 0 and n=0 in n = at + b)
10

11. Critical Gap (tc)
 Step function A reflects an assumption that:
 the regression line is a reflection of average driver behaviour but
 there is variance in driver behaviour (i.e. some drivers accept gaps less than the
gap size associated with point C) and
 therefore the critical gap size is assumed to be halfway between points t0 and C.
 For this assumption: tc(A) = t0 + 0.5tf
 Step function B is more conservative than function A (larger
value for tc).
 HCM based on the assumptions associated with step function A.
11

12. 12

13. Example:
 A gap use study has collected data for
vehicles making a left-hand turn from a
stop controlled minor street onto a one-
way 1-lane major street.
 Time headways were recorded between
each pair of consecutive vehicles on the
major street and the associated number of
minor street vehicles using the gap to
make a left turn.
 Data were collected for 1,460 vehicles
over a period of approximately 1 hour
and 45 minutes.
 The average gap size associated with
each number of vehicles using a gap is
shown in the next table
13

14. Solution
 regression coefficients: a = 0.30 and b = -1.2.
 Note: Do not use the data for 0 vehicles using a
gap
 tf = 1/a = 1/0.30 = 3.3 seconds
 t0 = -b/a = -(-1.2)/0.3 = 4 seconds
 tc = t0 + 0.5tf = 4 + 0.5*3.3 = 5.65 seconds
14

15. Important Note
 using the data for 0 vehicles using a gap
 a = 0.23 and b = -0.64
 tf = 4.3 seconds and
 tc = 5.0.
 These results are incorrect as they are biased by the
large number of gaps in which no minor street
vehicles were able to make their manoeuvre.
15

16. Distribution of Gap Sizes
 Please review lecture # 02
 Vehicle Arrival Patterns (Poisson Distribution)
 Exponential Distribution of Gaps
 Shifted Exponential Distribution of Gaps
16

17. Capacity Analysis for TWSC
intersections
 Capacity of a minor street movement is
governed by:
1) The number of gaps in the opposing stream.
2) Size of gaps.
3) Characteristics of drivers use of gaps (i.e. tc and tf)
4) Priority to use suitable gaps.
17

18. Interaction of Two Traffic Streams
 Cx = capacity of minor street movement x (vph)
18

19. Example:
 Consider the intersection of two one-way streets.
 Find the capacity of the minor street in vph.
 λmajor = 900 vph = 0.25 veh/second;
 (average headway) = 4 seconds per vehicle
 tc = 8 seconds; tf = 4 seconds
̅𝑡𝑡
19

20. Solution
20

21. Solution
A Number of vehicles using the associated gap
B Minimum gap size required for n vehicles to complete
manoeuvre
C Calculation of exponent term for the exponential
distribution
D Probability that headway is larger than the minimum
from column B
E Probability that headway permits exactly n vehicles to
complete their manoeuvre
F Number of gaps per hour that permit exactly n vehicles
to complete their manoeuvres
G Number of minor street vehicles per hour that
complete their manoeuvres using the associated gap
size
21

22. Interaction of More Than Two streams
 If streams are independent of
each other, then
 the probability of finding a
suitable gap in both streams
simultaneously is equal to
 the product of the probability
of finding a suitable gap in
each stream individually.
22

23. Priority of traffic streams
 When calculating the capacity of movements
for an intersection with more than two traffic
streams, one must consider the rank/priority of
that movement
 For North America the HCM is the standard
commonly used for TWSC analysis
 Exhibit 17-3 illustrates the ranks of the
different possible intersection movements
23

24. 24

25. 25

26. Example
 tc = 8 seconds; tf = 4 seconds for both minor street
movements.
 λ 2 = 900 vph; λ9 = 100 vph; λ10 = 60 vph.
 Determine:
 (a) the capacity of movement 9 and
 (b) the capacity of movement 10.
26

27. Solution: part (a)
 Movement 9 must yield right of way to movement
2 only
 capacity is a function of λ2 and not λ10.
 The opposing volume of 900 vph and the critical
gap and follow up times are the same as used in the
previous example,
 capacity of movement 9 = 192 vph.
27

28. Solution: part (b)
 The capacity of movement 10 ≠ 192 vph because
 movement 9 uses some of the available gaps making them
unavailable for movement 10.
 We call this effect “impedance”.
 The magnitude of this effect depends on the arrival rate and
capacity of higher ranked movements.
 The probability that a vehicle attempting to make
movement 9 will be waiting for a gap can be estimated as
 the ratio of the demand for gaps by vehicles making movement
9 (i.e. λ9) and the capacity associated with movement 9 (cm,9).
 Therefore, the probability that there is no vehicle waiting to
make movement 9 (P0,9 ) when a gap becomes available for
a vehicle making movement 10 is:
28

29.  P0,9 = probability that there is no queue waiting to
make movement 9
 λ9 = arrival rate for movement 9 (vph)
 cm,9 = capacity of movement 9 (vph)
 The potential capacity (cp) of movement 10 = 192 vph,
since this is the capacity if none of the available gaps
were used by vehicles of movement 9.
 The actual movement capacity must include the
impedance effect and is computed as
 cm,10 = 192 vph x 0.48 = 92 vph.
29

30. HCM equation for determining capacity
30

31. Conflicting volumes (HCM 2000)
31

32. Conflicting volumes (HCM 2000)
32

33. Conflicting volumes (HCM 2000)
33

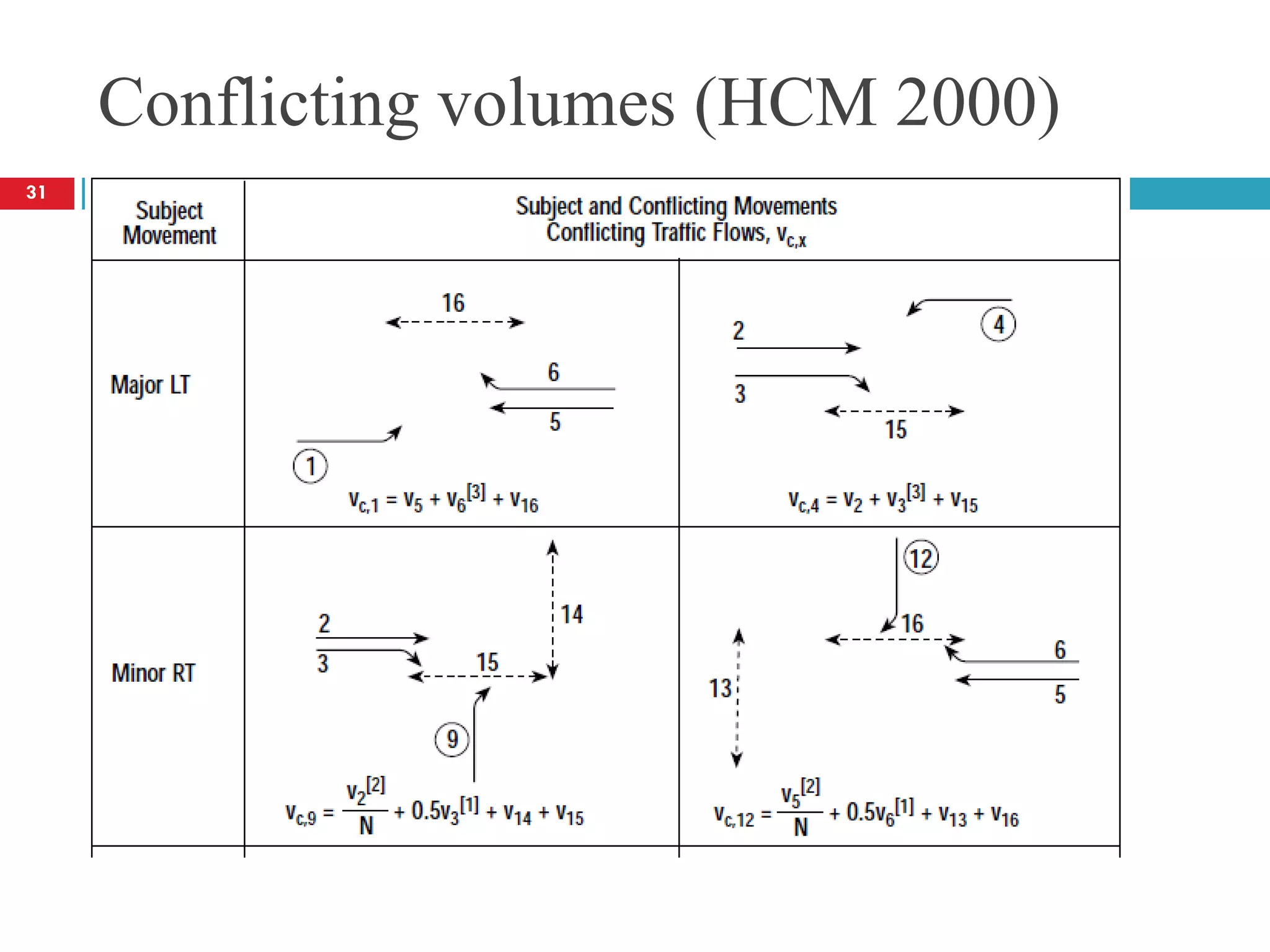
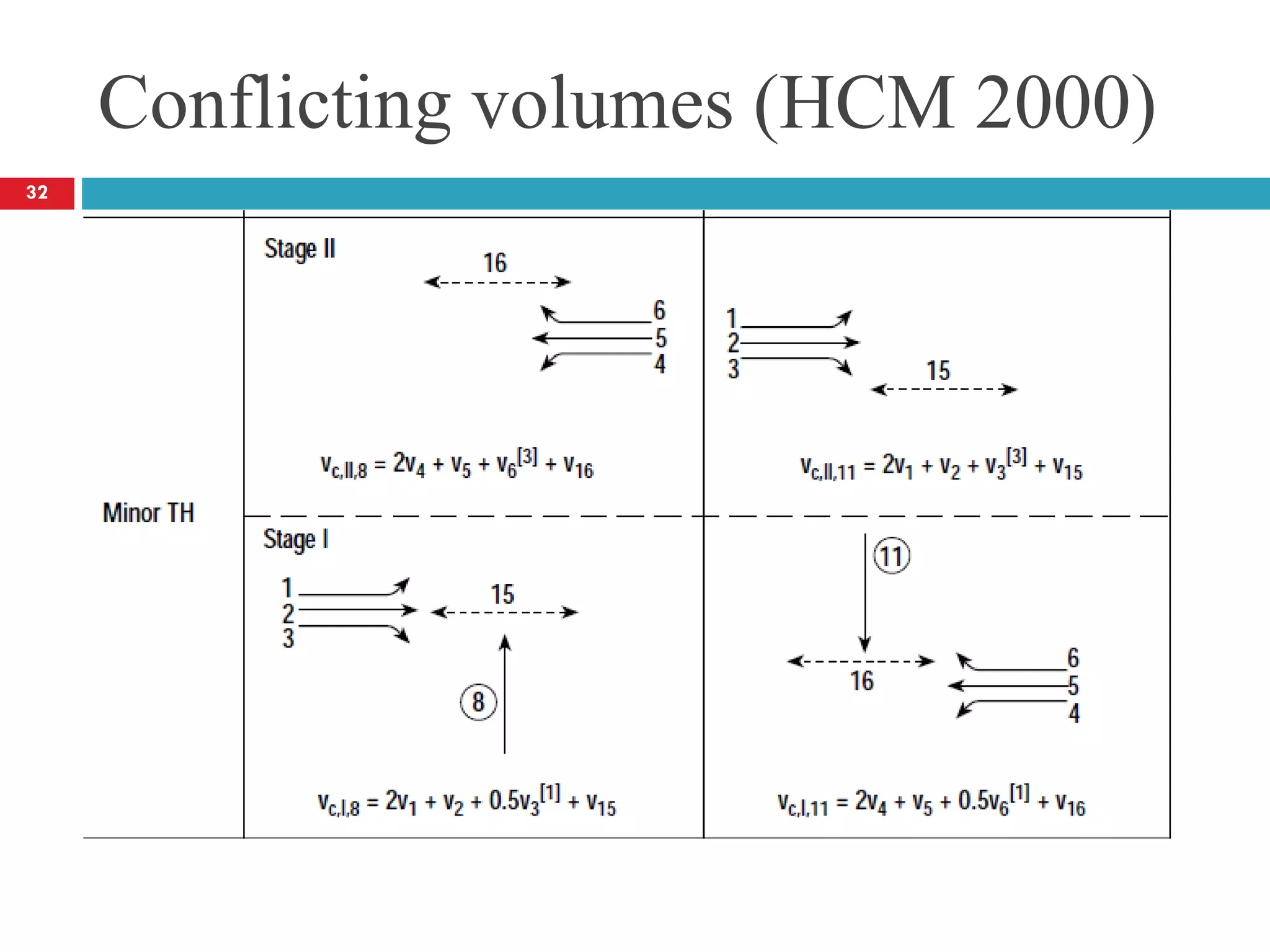
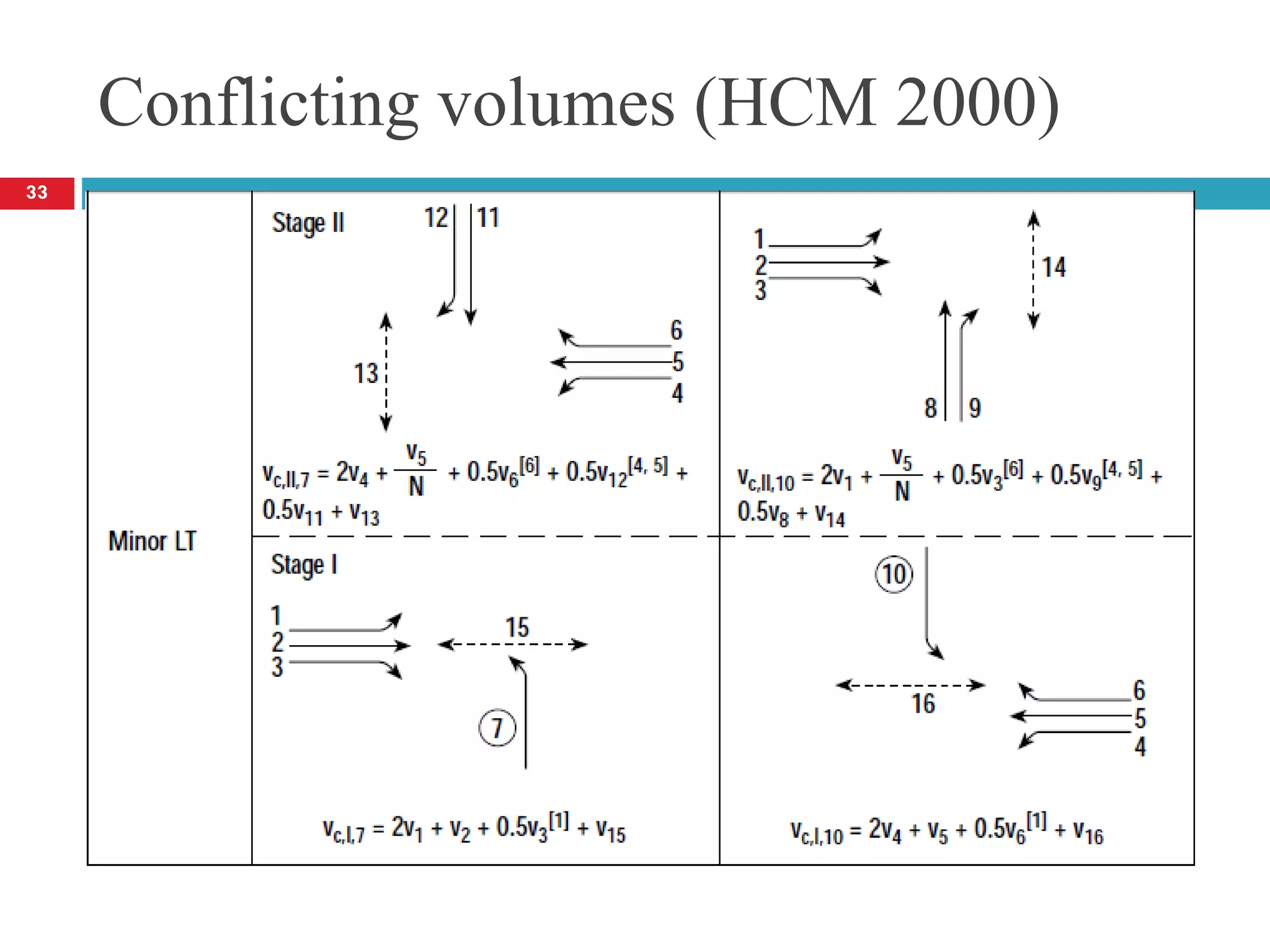
34. Conflicting volumes (HCM 2000)
 [1] If there is a right-turn lane on the major street, v3 or v6 should not be
considered.
 [2] If there is more than one lane on the major street, the flow rates in the
right lane are assumed to be v2/N or v5/N, where N is the number of through
lanes. The user can specify a different lane distribution if field data are
available.
 [3] If right-turning traffic from the major road is separated by a triangular
island and has to comply with a yield or stop sign, v6 and v3 need not be
considered.
 [4] If right-turning traffic from the minor road is separated by a triangular
island and has to comply with a yield or stop sign, v9 and v12 need not be
considered.
 [5] Omit v9 and v12 for multilane sites, or use one-half their values if the
minor approach is flared.
 [6] Omit the farthest right-turn v3 for subject movement 10 or v6 for subject
movement 7 if the major street is multilane.
34

35. Conflicting volumes (HCM 2000)
35

36. HCM critical gap equation
36

37. HCM follow-up time equation
37

38. Adjustments on tc and tf
Adjustment Values
tcHV 1.0, Two-lane major street
2.0, Four-lane major street
tcG 0.1, Movements 9 and 12
0.2, Movements 7, 8, 10 and 11
1.0, Otherwise
tcT 1.0, With two stage process
0.0, With single stage process
t3LT 0.7, Minor-street LT at T-intersection
0.0, Otherwise
tfHV 0.9, Two-lane major street
1.0, Four-lane major street
LTcTcGHVcHVcbc ttGtPttt 3−−++=
HVfHVfbf Pttt +=
38

39. Considering Impedance
 Rank 2 movements
39

40. Considering Impedance
 Then the capacity for the Rank 3 movement is
computed as
 Rank 3 movements
40

41. Considering Impedance
 Rank 4 movements
41

42. Shared Lanes
42

43. Control Delay
43

44. Length of Queues
44

45. Example
 Consider the three-leg intersection illustrated below.
Determine the average control delay and the resulting level
of service for the minor street approach.
 Assume:
 no heavy vehicles,
 no pedestrians, and
 all approaches are level (i.e. 0% grade).
 Assume an evaluation time period of 15 minutes and that
 the major street can be considered to be a two-lane roadway.
45

46. Solution
 We begin the analysis by denoted the rank of each
movement as follows:
 Rank Movement
 Rank 1: 2, 3, 5
 Rank 2: 4, 9
 Rank 3: 7
46

47. Step 1: Rank 2 movements
 RT from Minor Street (9)
 Note: Separate right turn lane on major street therefore don’t
include v3.
 vc,9 = 250 vph
 tc,9 = 6.2 seconds
 tf,9 = 3.3 seconds
 cp,9 = 794 vph
 cm,9 = 794 vph
 LT from Major Street (4)
 vc,4 = v3 +v2 = 40 + 250 = 290 vph
 tc,4 = 4.1 seconds
 tf,4 = 2.2 seconds
 cp,4 = 1283 vph
 cm,4 = 1283 vph t t t t
47

48. Step 2: Rank 3 movements
 LT from Minor Street (7)
 Note that a separate turning lane is provided for movement 3, therefore
v3 need not be included when calculating vc,7.
 vc,7 = v2 +v5 + 2v4= 250 + 300 + 2(150) = 850 vph
 tc,4 = 7.1 – 0.7 = 6.4 seconds (Adjustment for T intersection)
 tf,4 = 3.5 seconds
 cp,4 = 334 vph
 Must consider impedance created by Major Street LT vehicles.
 Normally, the minor street LT movement (7) is rank 4 and must
consider the impedance impacts from all higher priority streams
including 1, 4, and 11.
 However, for a T-intersection, movement 7 is rank 3 and is impeded
only by movement 4 (LT from major street).
 f7 = 1 – v4/cm,4 = 1 – 150/1283 = 0.88
 cm,7 = cm,7 × f7 = 334 × 0.88 = 294 vph
48

49. Step 3: Determine Shared Lane Capacity
,
40 120
540
40 120
294 794
y
y
sh
y
y m y
V
C
V
C
+
= =
  +  
 
∑
∑
49

50. Step 4: Determine Delay
 Movement 4 (LT Major)
 cm,4 = 1283 vph
 v4 = 150 vph
 T = 0.25 hour
50

51. Step 4: Determine Delay
 Movement 7 & 9 (LT & RT Minor)
 csh = 540 vph
 vsh = v7 + v9 = 40 + 120 = 160 vph
 T = 0.25 hour
 d = 14.0 seconds
51

52. Step 5: Determine Level of Service
 Movement 4 LOS = A
 Movements 7 & 9 LOS = B
52

53. Step 6: Determine Average Queue Length
 Movement 4 (LT Major)
 Q4 = 8.2 × 150/3600 = 0.34 vehicles
 Movement 7 & 9 (LT & RT Minor)
 Qsh = 14.0 × 160/3600 = 0.62 vehicles
53

54. Home Reading
 Chapter # 17 in HCM 2000
54

55. Thanks for your time
55