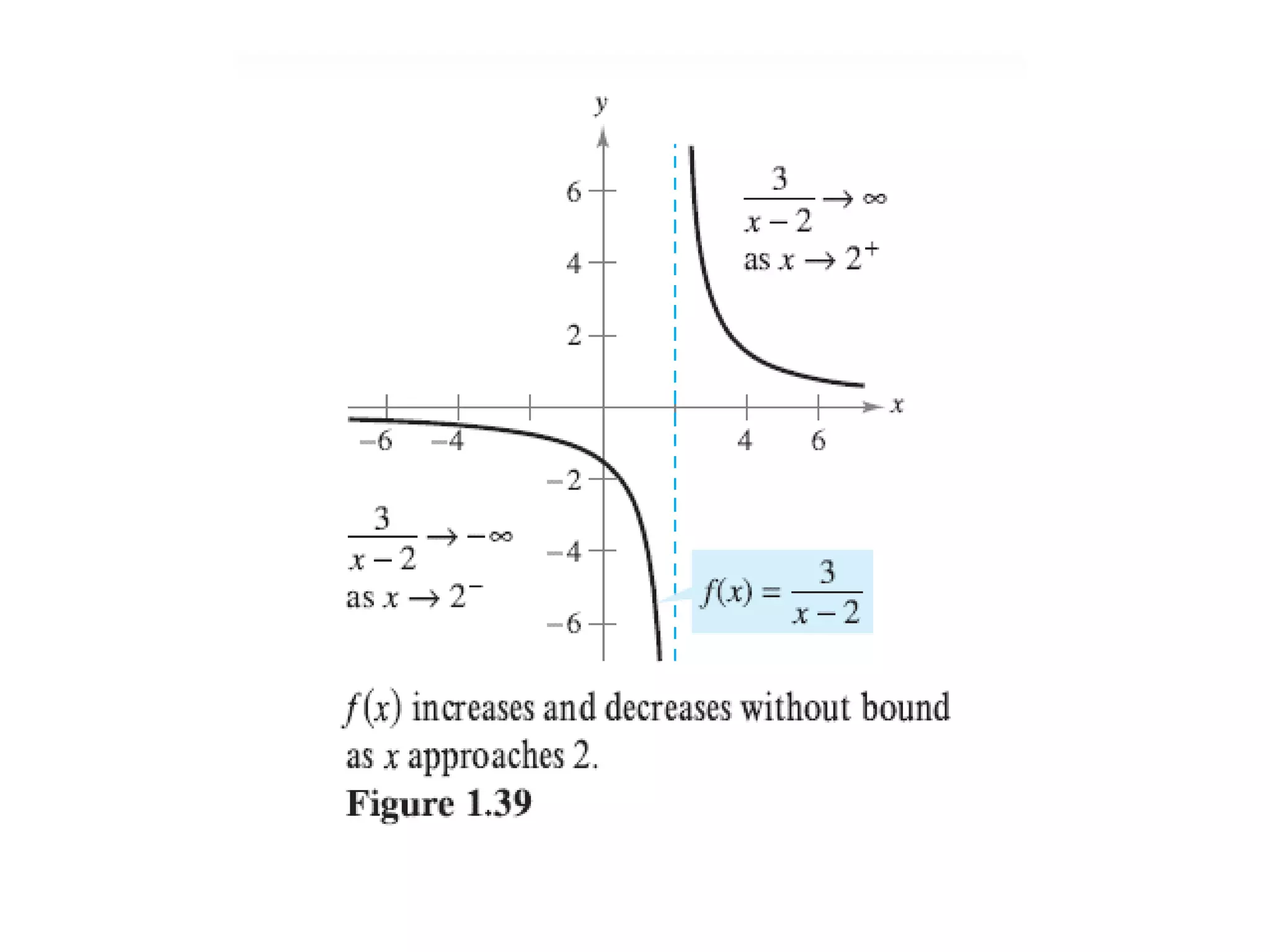
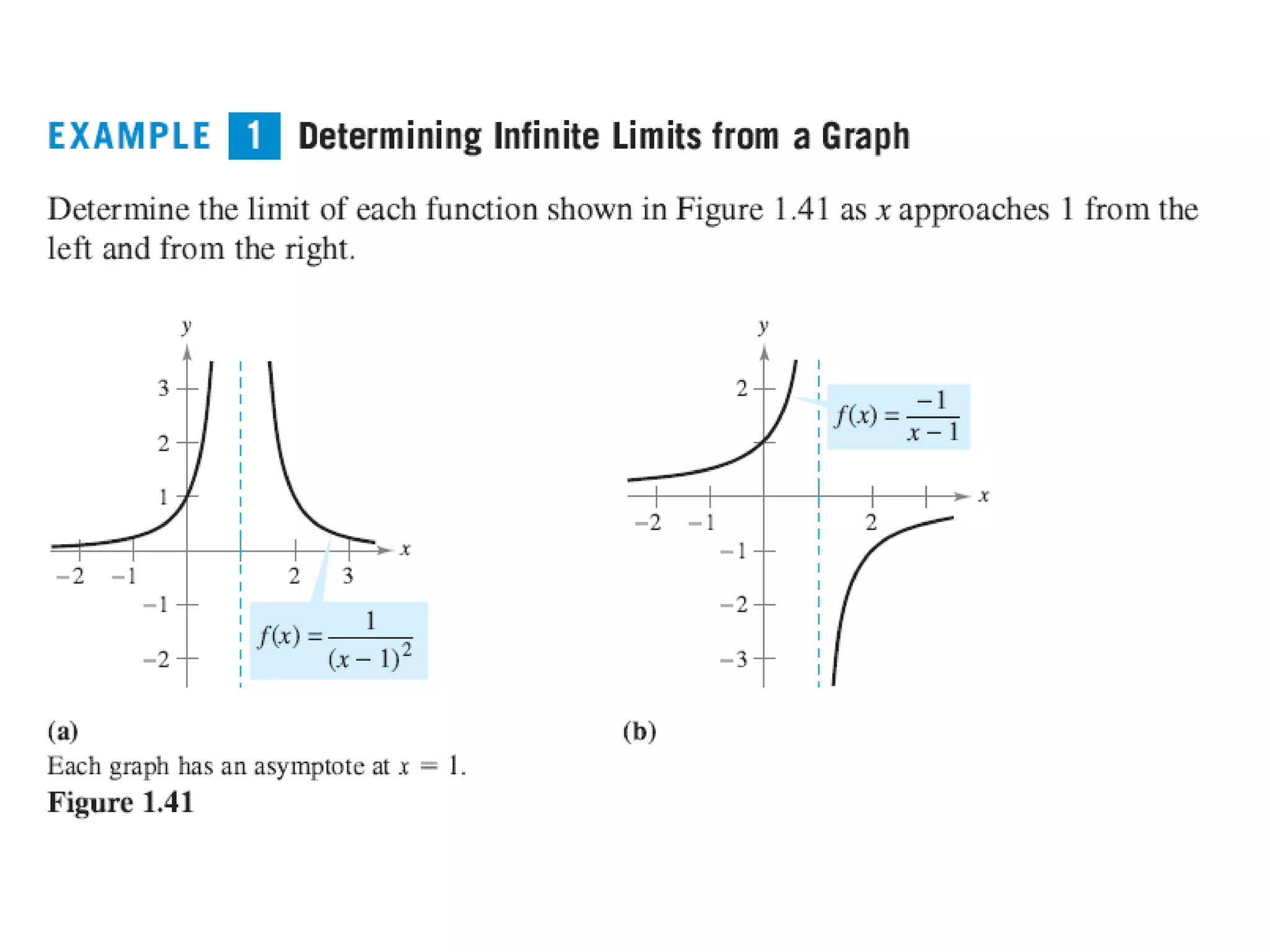
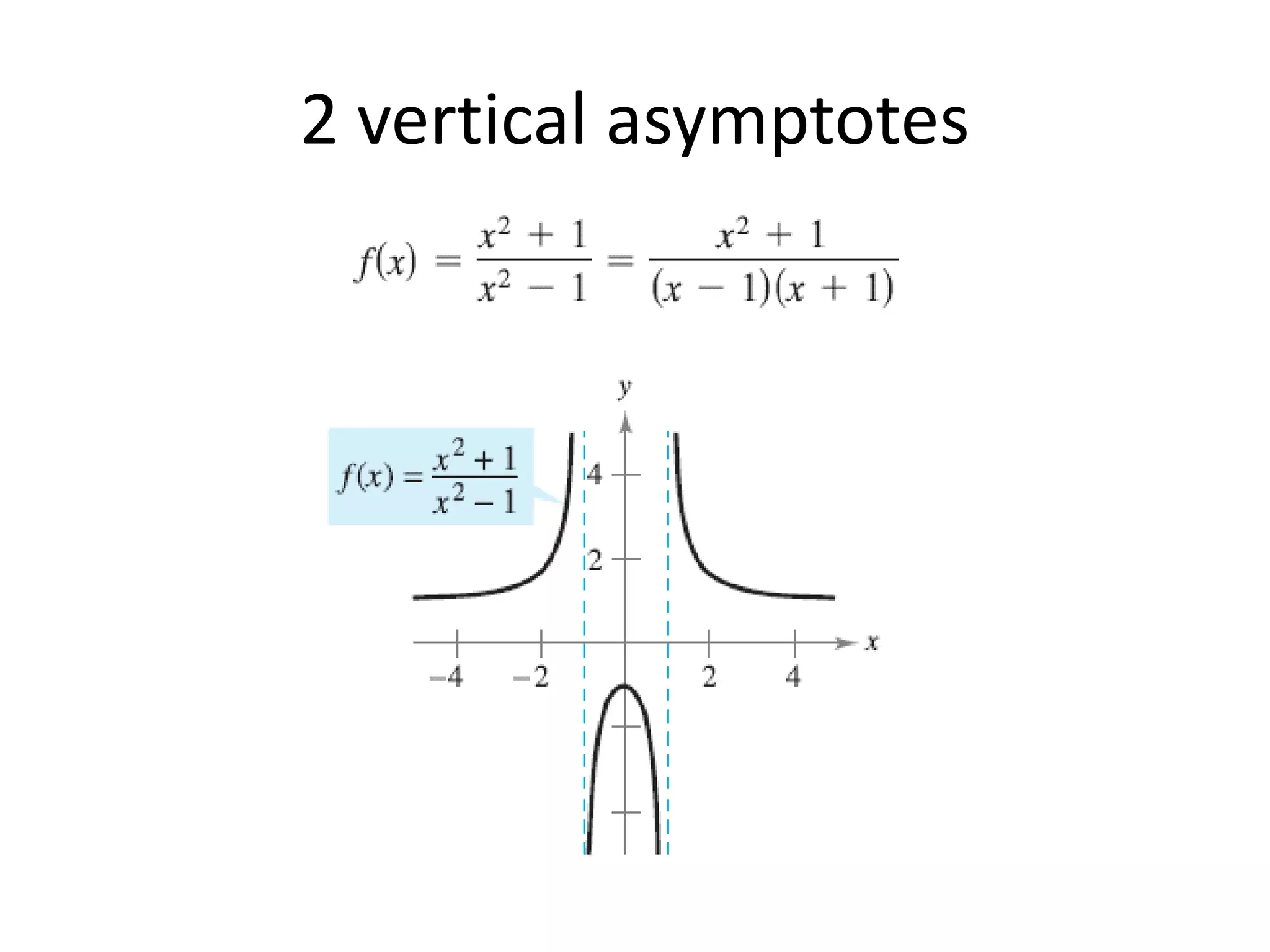
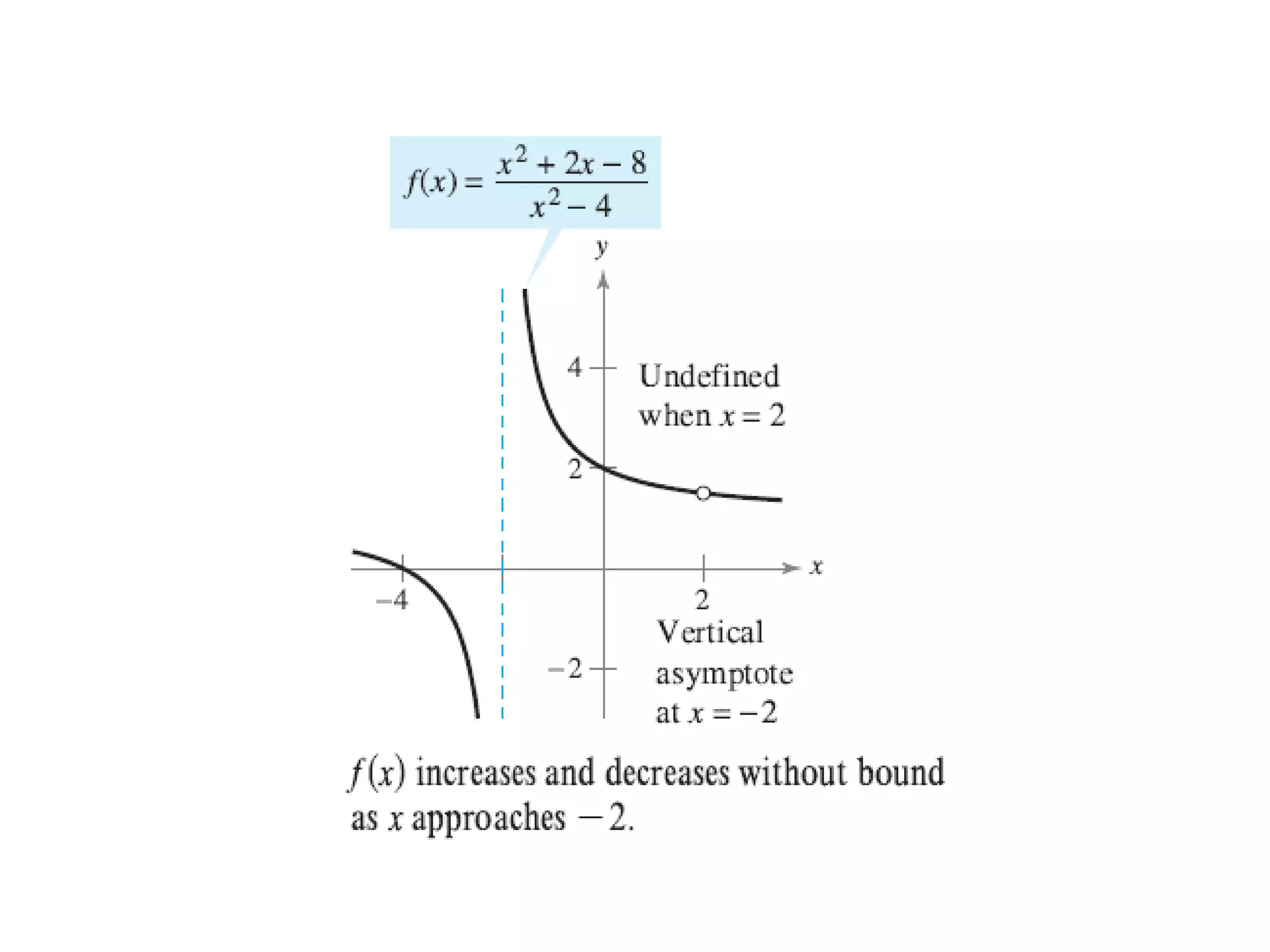
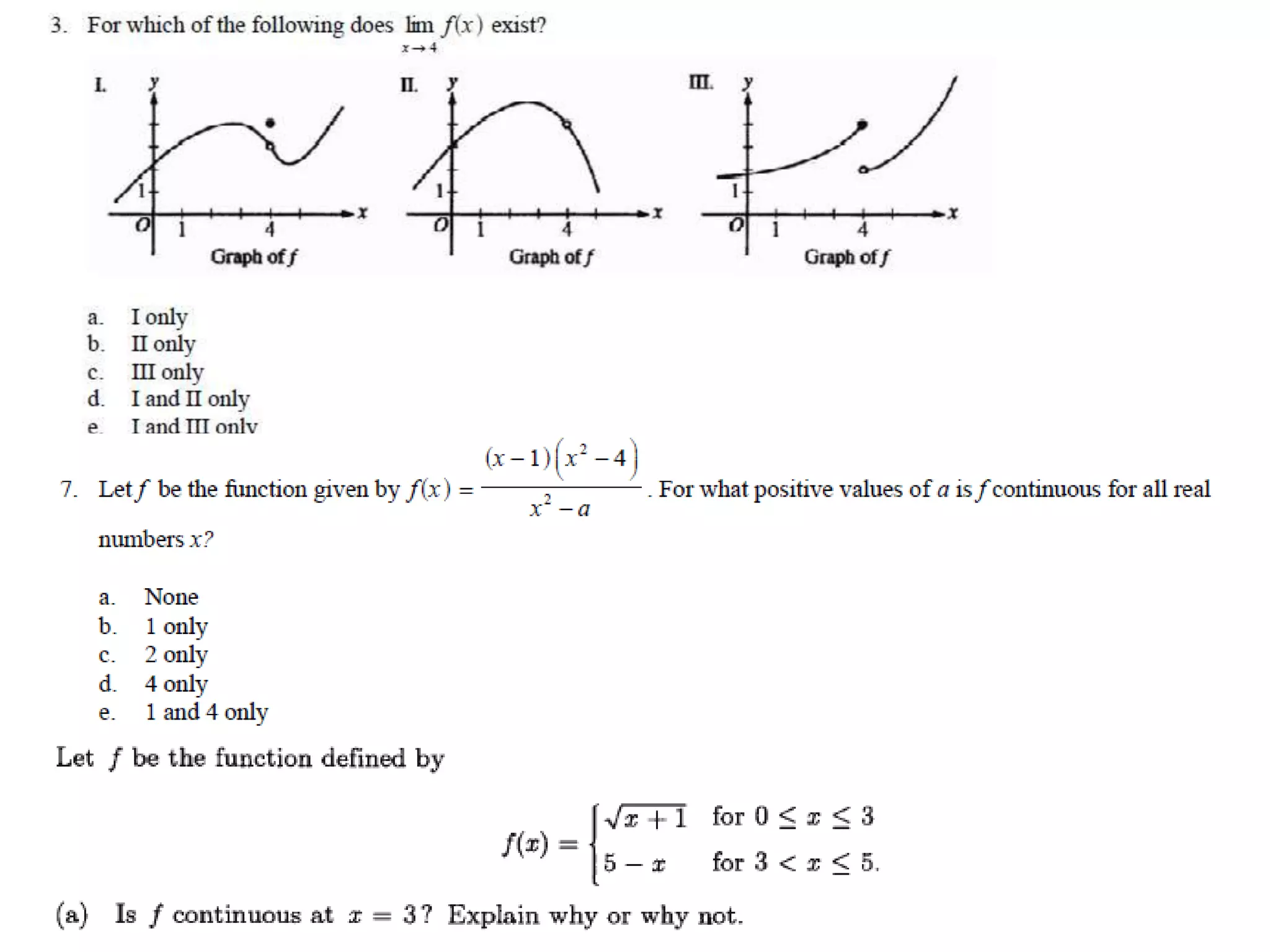
This document discusses vertical and horizontal asymptotes of functions: - Vertical asymptotes occur when the denominator is undefined, causing the limit of the function to be plus/minus infinity. - Horizontal asymptotes describe the end behavior of a graph and are found by comparing the degrees of the numerator and denominator. - Examples show how to find vertical and horizontal asymptotes by analyzing functions' forms.

1. The Lame Joke of the day..
What do cats eat for breakfast?
And now it’s time for..
Mice Krispies!

2. Vertical Asymptotes
• Vertical asymptotes occur when a function is
undefined (usually the zeros of the denom.)
• At a vertical asymptotes, the limit of the
function is +/- infinity ( does not exist)
• At the asymptote, the function increases or
decreases without bound.
• Also, )(lim)(lim xfxf
cxcx 



5. 2 vertical asymptotes

6. Practice
Find the vertical asymptotes of each function:
1
1
)(


x
xf
3
)2(
4
)(


x
xf
16
2
)( 4
2



t
tt
xf

7. Vertical Asymptotes - exceptions
• The exception is when you can cancel
common factors - YOU get a hole instead of
an asymptote

10. Limits at infinity
• How do you find the limit of a function when x
approaches +/- infinity?
– YOU FIND THE HORIZONTAL ASYMPTOTES
Tells you the end behavior of the graph.)(lim xf
x 

11. How do we find the horizontal
asymptotes?
• Compare the degrees of the numerator and
denominator.
Degrees equal: It’s the ratio of the leading
coefficients.
Degree of numerator is greatest: No asymptote. The
function is unbounded at the ends. (Goes on forever
to infinity)
Degree of denominator is greatest: y = 0 (x-axis) is
horizontal asymptote

12. Example
1
12
lim


 x
x
x

13. Example
13
52
lim 2


 x
x
x

14. Example
13
52
lim 2
3


 x
x
x

15. Practice
Evaluate each limit
xx
1
lim

13
23
lim
2


 x
x
x
13
25
lim 4
4


 x
xx
x

16. AP Calculus Warm up