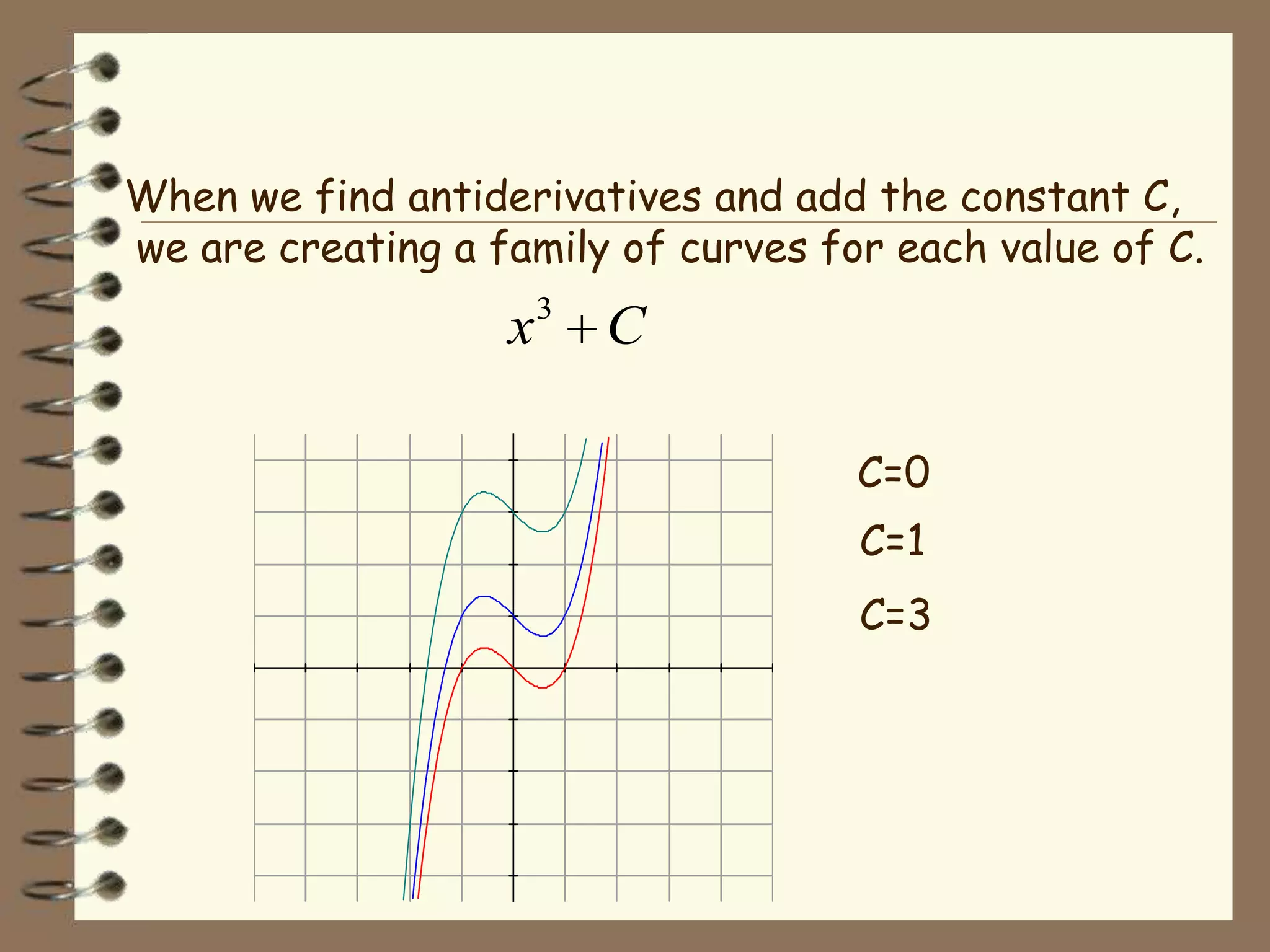
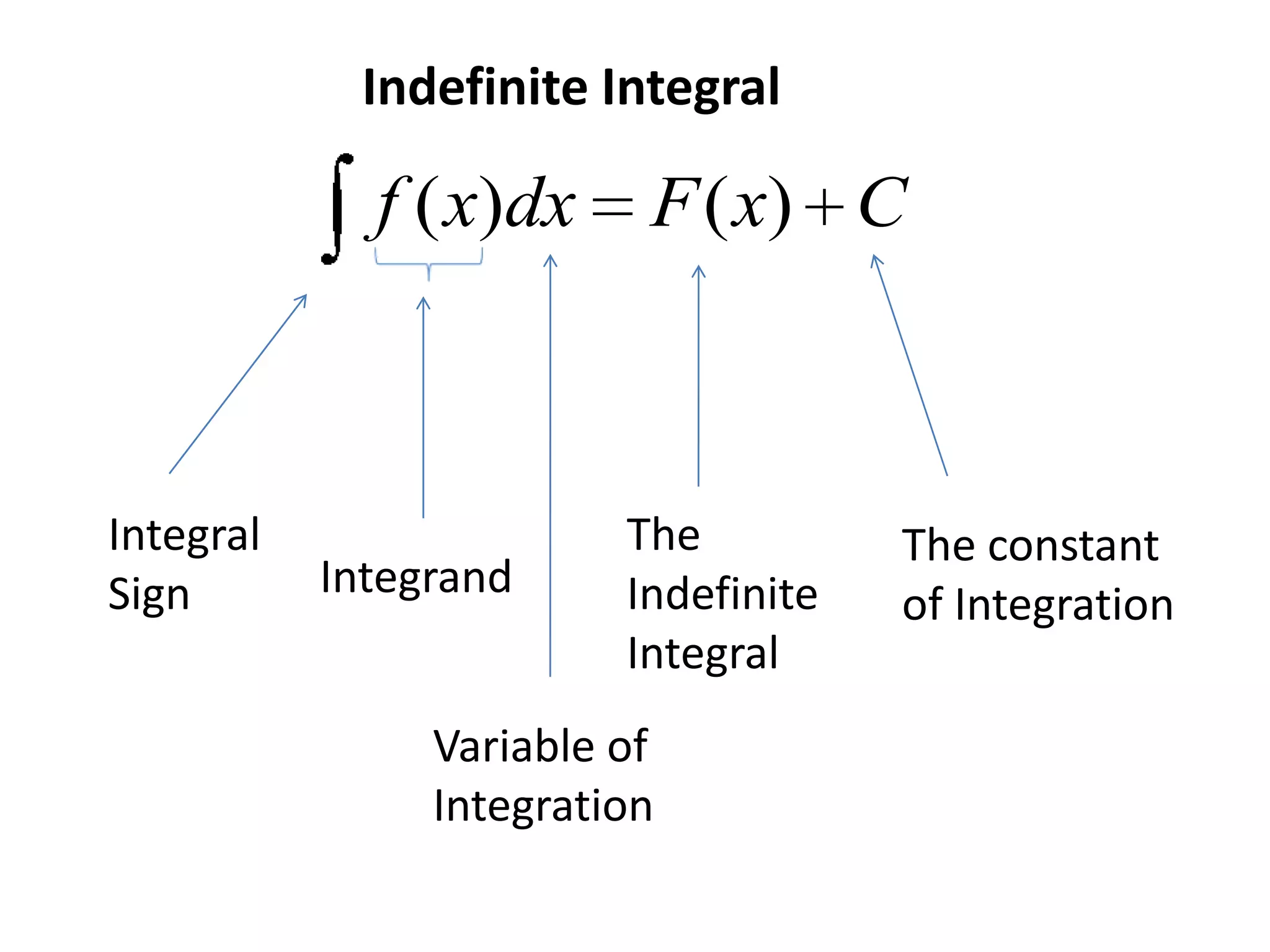
This document contains information about integration and antiderivatives. It discusses how integration undoes differentiation, finds areas, volumes, centers of mass, and position given acceleration or velocity. It also discusses that antiderivatives form a family of curves where changing the constant C results in different curves with the same derivative. Examples are provided to demonstrate basic integration rules and solving application problems using integrals.

1. Drive activity
• Please submit your drive activities.

2. Sec. 4.1: Antiderivatives

3. Uses of integration
1.
2.
3.
4.
5.
“Undoes” differentiation.
Finds the area under a curve.
Finds the volume of a solid.
Finds the center of mass.
Finds s(t) given a(t) or v(t).
*** and many more….

4. The Uniqueness of Antiderivatives
2
Suppose f x
3x , find an antiderivative of f. That is,
2
find a function F(x) such that F ' x
3x .
F x
x
3
Using the Power Rule in
Reverse
Is this the only function whose derivative is 3x2?
H x
H' x
x
3
5
3x 2
K x
x
3
11
3x 2
K' x
M x
M' x
x
3
3x 2
There are infinite functions whose derivative is 3x2
whose general form is:
C is a constant real
G x
3
x
C
number (parameter)

5. When we find antiderivatives and add the constant C,
we are creating a family of curves for each value of C.
x3 C
C=0
C=1
C=3

6. Indefinite Integral
f ( x)dx
Integral
Sign
Integrand
F ( x) C
The
Indefinite
Integral
Variable of
Integration
The constant
of Integration

7. Indefinite Integral
The indefinite integral gives a family of functions!
(Not a value)
The indefinite integral always has a constant!
Vs.
The definite integral (later) gives a numerical
value.

8. Summary
Integration is the “inverse” of differentiation.
d
F ( x) dx
dx
F ( x) C
Differentiation is the “inverse “ of integration.
d
dx
f ( x)dx
f ( x)

9. Basic Integration Rules
0dx
C
kdx
kx C
k f ( x )dx
k f ( x )dx

10. Basic Integration Rules
f ( x ) g ( x ) dx
f ( x )dx
n 1
n
x dx
x
C
n 1
Power Rule
g ( x )dx

11. Basic Integration Rules
cos xdx
sin xdx
2
sec xdx
sin x C
cos x C
tan x C

12. Basic Integration Rules
2
csc xdx
sec x tan xdx
csc x cot xdx
cot x C
sec x C
csc x C

13. Examples
Find each of the following indefinite integrals.
5
a.
x dx
b.
5 x3 dx
x
sin x dx
c.
1
6
d.
1
x
6
C
cos x C
5
4
x4
C
dx 2 x C

14. Application problem
• A ball is thrown upward with an initial
velocity of 64 ft/ sec from an initial height
of 80 feet.
a. Find the position function, s(t)
b. When does the ball hit the ground?

15. Example
A particle moves along a coordinate axis in such a way that
3
its acceleration is modeled by a t
2t for time t > 0.
If the particle is at s = 5 when t = 1 and has velocity v = - 2
at this time, where is it when t = 4?
Integrate the acceleration to find velocity:
v t
2t
3
dt
2 t
3
1
3 1
2
dt
t
3 1
t
2
t
C
2
C
Use the Initial Condition to find C for velocity:
2
1
2
C
C
v t
1
1
Integrate the Velocity to find position:
s t
t
5
1
2
1
Answer the
Question:
1 dt
t 2 dt
1
2 1
1 dt
t
2 1
1t C t
Use the Initial Condition to find C for position:
1 C
s 4
C
4
1
4 5
5
1.25
s t
t
1
1
t C
t 5