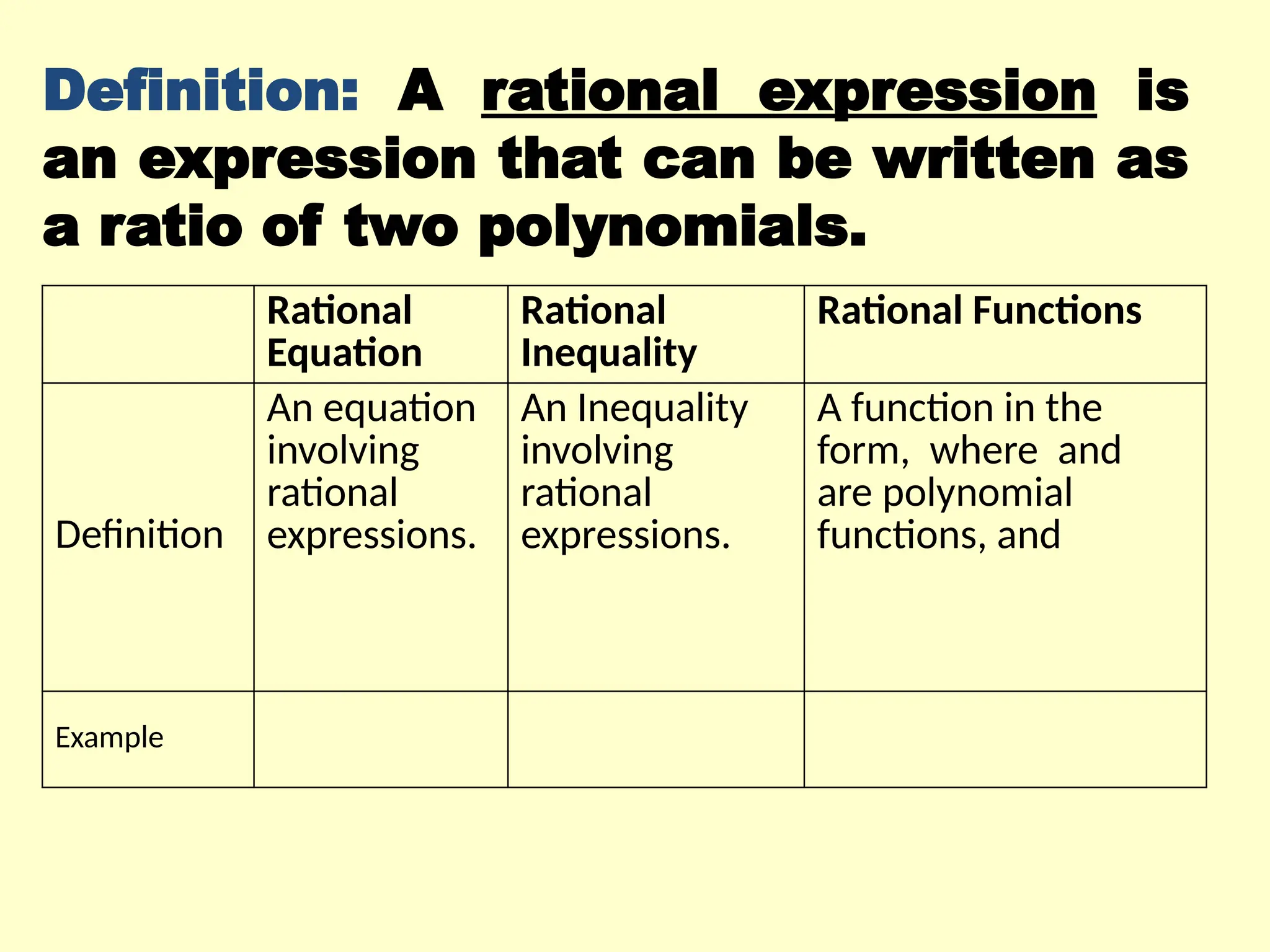
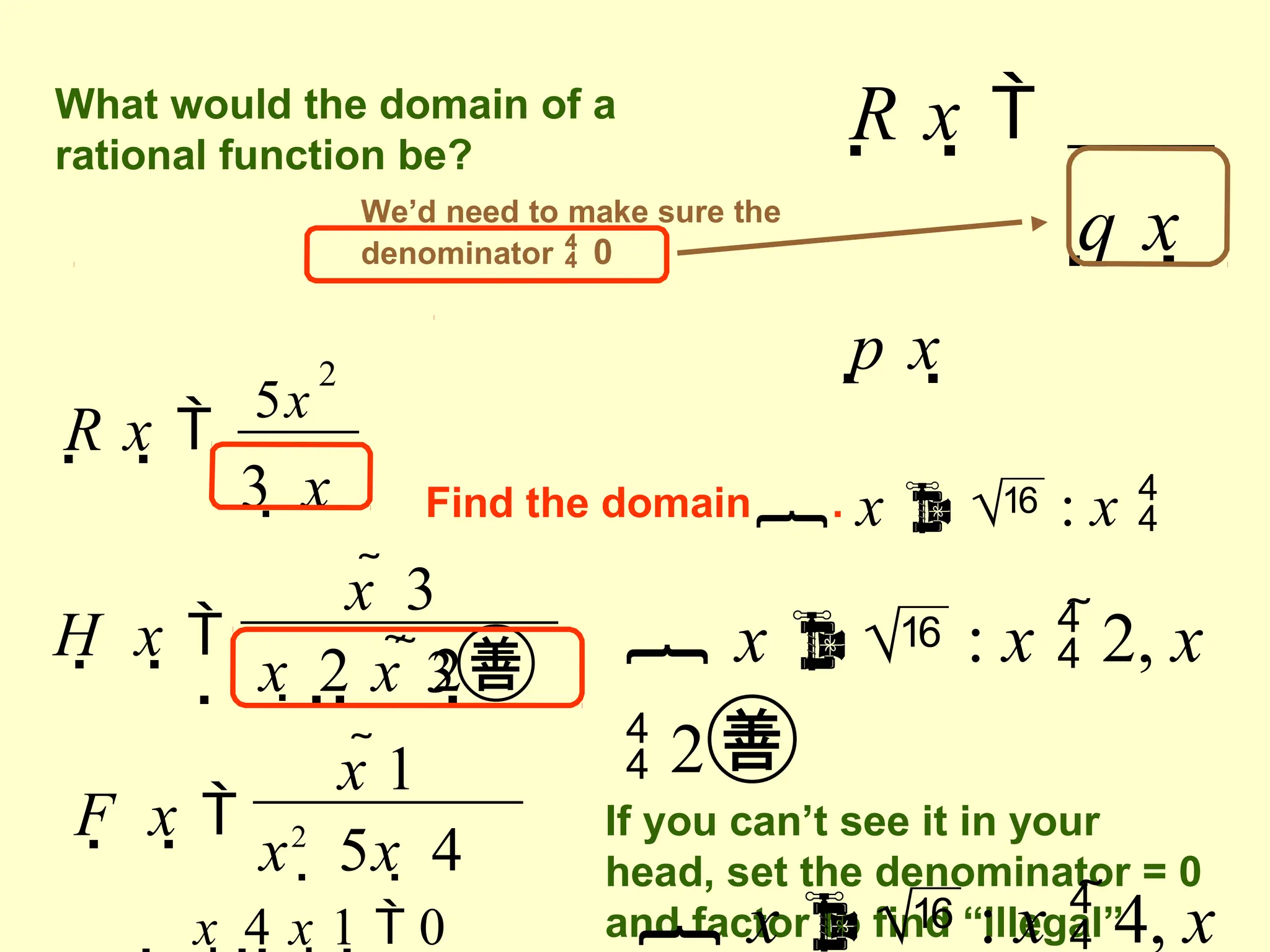
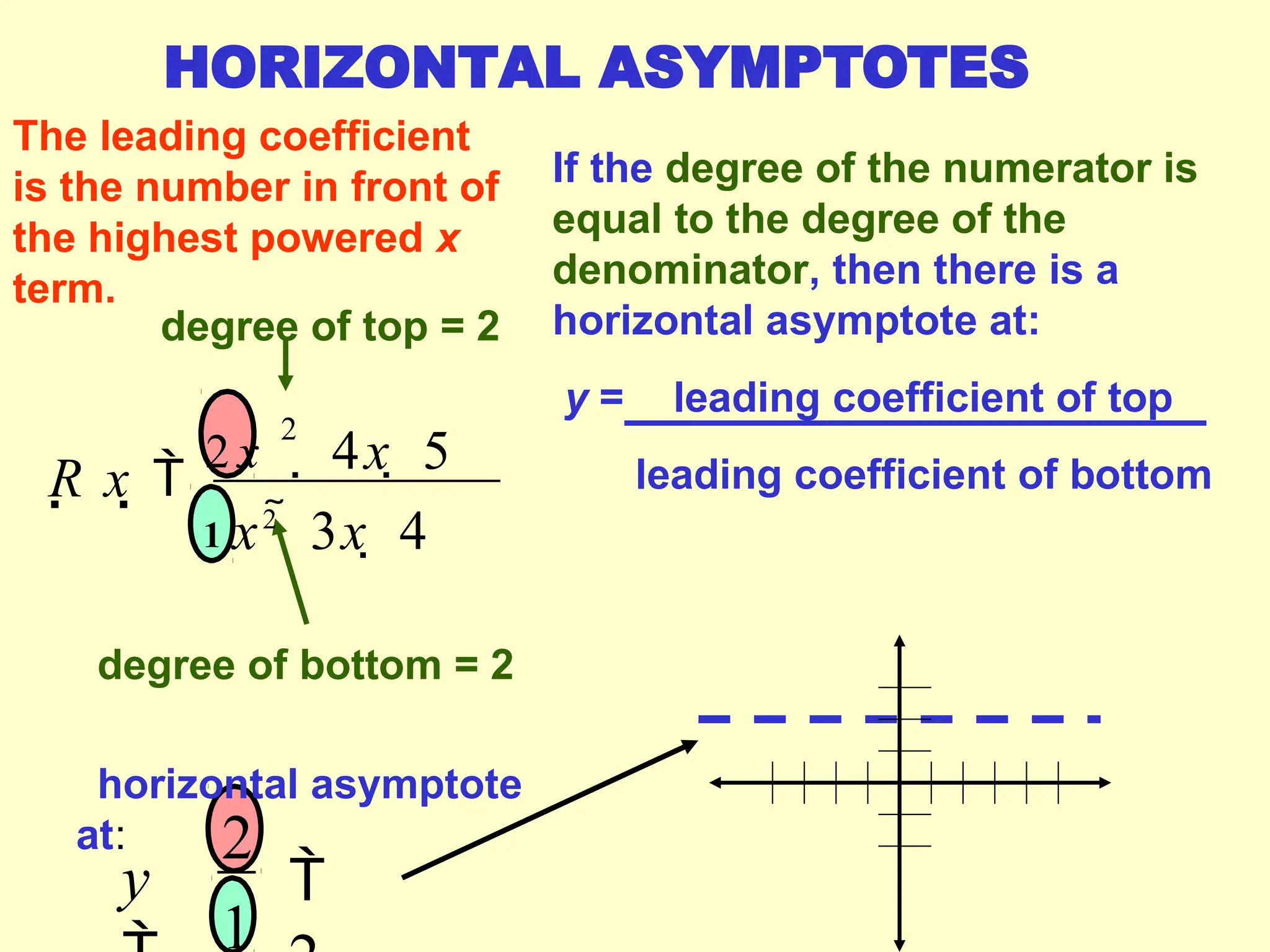
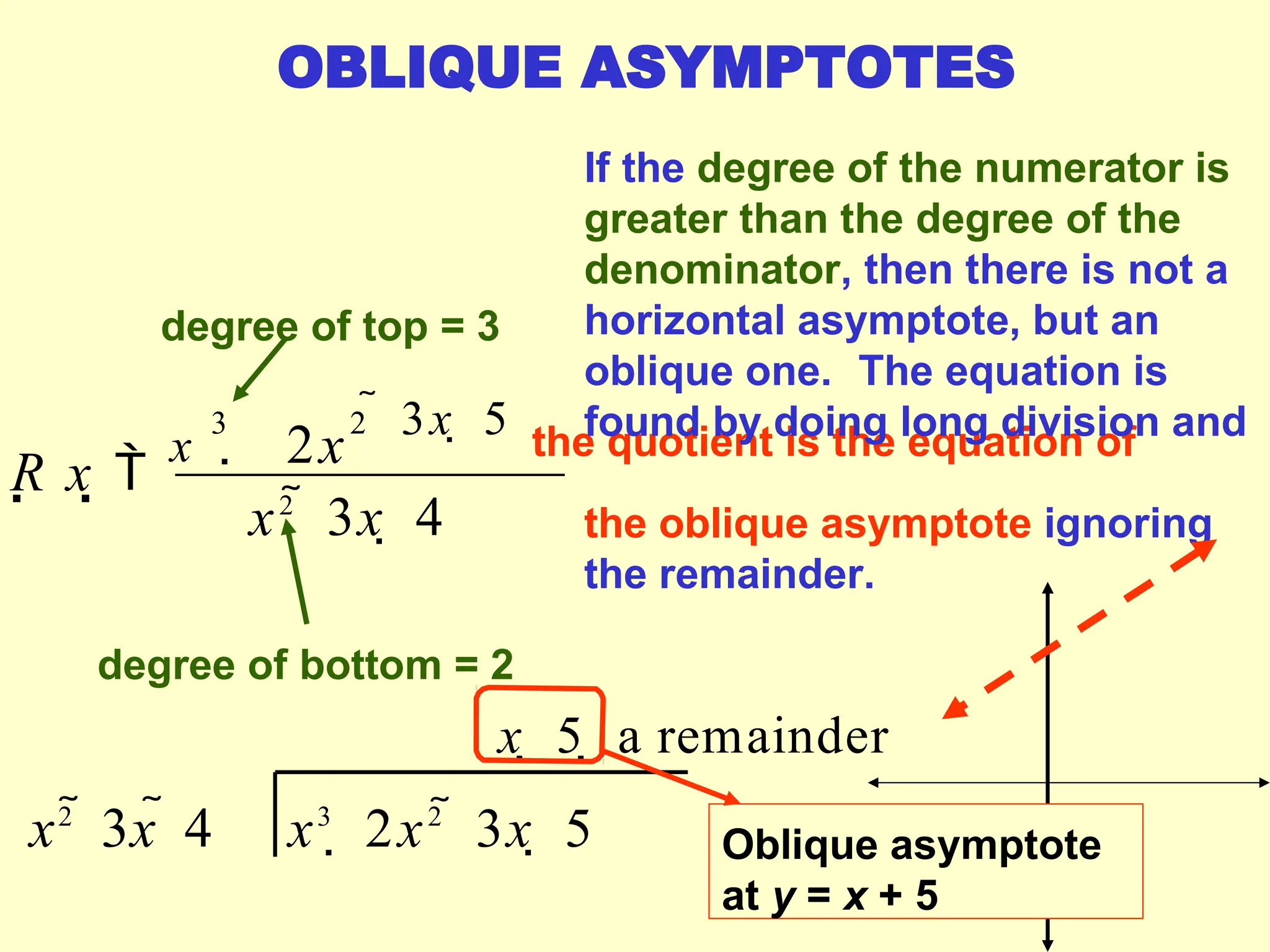
Rational functions are expressed as the ratio of two polynomials, and their domain excludes values that make the denominator zero. Vertical asymptotes occur at 'illegal' x values where the denominator equals zero, while horizontal and oblique asymptotes are determined by comparing the degrees of the numerator and denominator. To find these asymptotes, specific conditions based on the degree relationship must be met, with horizontal asymptotes involving the x-axis or leading coefficients and oblique asymptotes derived from polynomial long division.

1. RATIONAL
FUNCTIONS
A rational function is a function of the form:
R x 
p x
q x
where p and q
are polynomials
and q ≠ 0

2. Definition: A rational expression is
an expression that can be written as
a ratio of two polynomials.
Rational
Equation
Rational
Inequality
Rational Functions
Definition
An equation
involving
rational
expressions.
An Inequality
involving
rational
expressions.
A function in the
form, where and
are polynomial
functions, and
Example

3. Domain of Rational Functions
• The domain of a rational function is set
of all real numbers, except those that
make the denominator zero.
• Written as
Example:
S
=0
=5
Therefore,

4. R x 
p x
q x
What would the domain of a
rational function be?
We’d need to make sure the
denominator  0
R x 
5x
3  x
2
Find the domain. x   : x 
3
H  x 
 x  2 x  2
x  3
 x  : x  2, x
 2
If you can’t see it in your
head, set the denominator = 0
and factor to find “illegal”
F  x 
x2
 5x  4
x 1
 x  4 x 1  0  x  : x  4, x

5. Finding Asymptotes
VERTICAL
ASYMPTOTES
There will be a vertical asymptote at any
“illegal” x value, so anywhere that would make
the denominator = 0
R x 
x
 xx2
43xx14 0
 2x  5
2
Let’s set the bottom = 0
and factor and solve to
find where the vertical
asymptote(s) should be.
So there are vertical
asymptotes at x = 4
and x = -1.

6. If the degree of the numerator is
less than the degree of the
denominator, (remember degree
is the highest power on any x
term) the x axis is a horizontal
asymptote.
If the degree of the numerator is
less than the degree of the
denominator, the x axis is a
horizontal asymptote. This is
along the line y = 0.
We compare the degrees of the polynomial in the
numerator and the polynomial in the denominator to tell
us about horizontal asymptotes.
R x 
x2
 3x  4
2x  5
degree of bottom = 2
HORIZONTAL ASYMPTOTES
degree of top = 1
1
1 < 2

7. If the degree of the numerator is
equal to the degree of the
denominator, then there is a
horizontal asymptote at:
y = leading coefficient of top
leading coefficient of bottom
degree of bottom = 2
horizontal asymptote
at:
HORIZONTAL ASYMPTOTES
degree of top = 2
The leading coefficient
is the number in front of
the highest powered x
term.

1 x2
 3x  4
R x 
2 x  4x  5
2
1
2
y

8. R x 
x
x2
 3x  4
 3x  5 the quotient is the equation of
 2x
2
3
If the degree of the numerator is
greater than the degree of the
denominator, then there is not a
horizontal asymptote, but an
oblique one. The equation is
found by doing long division and
the oblique asymptote ignoring
the remainder.
degree of bottom = 2
x  5  a remainder
OBLIQUE ASYMPTOTES
degree of top = 3
x2
 3x  4 x3
 2x2
 3x  5 Oblique asymptote
at y = x + 5

9. SUMMARY OF HOW TO FIND ASYMPTOTES
Vertical Asymptotes are the values that are NOT in the
domain. To find them, set the denominator = 0 and
solve.
To determine horizontal or oblique asymptotes, compare
the degrees of the numerator and denominator.
1. If the degree of the top < the bottom, horizontal
asymptote along the x axis (y = 0)
2. If the degree of the top = bottom, horizontal asymptote
at y = leading coefficient of top over leading
coefficient of bottom
3. If the degree of the top > the bottom, oblique
asymptote found by long division.