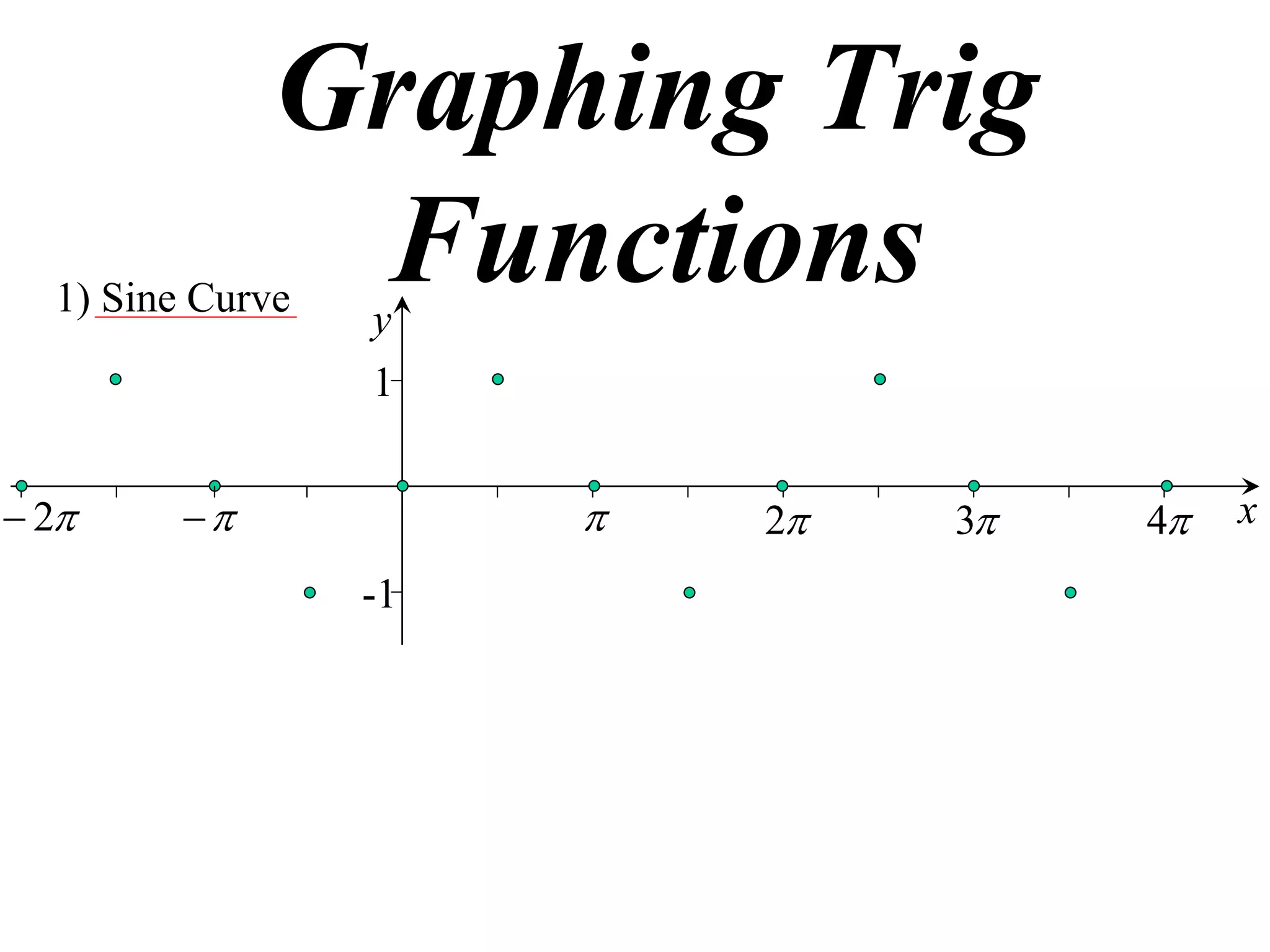
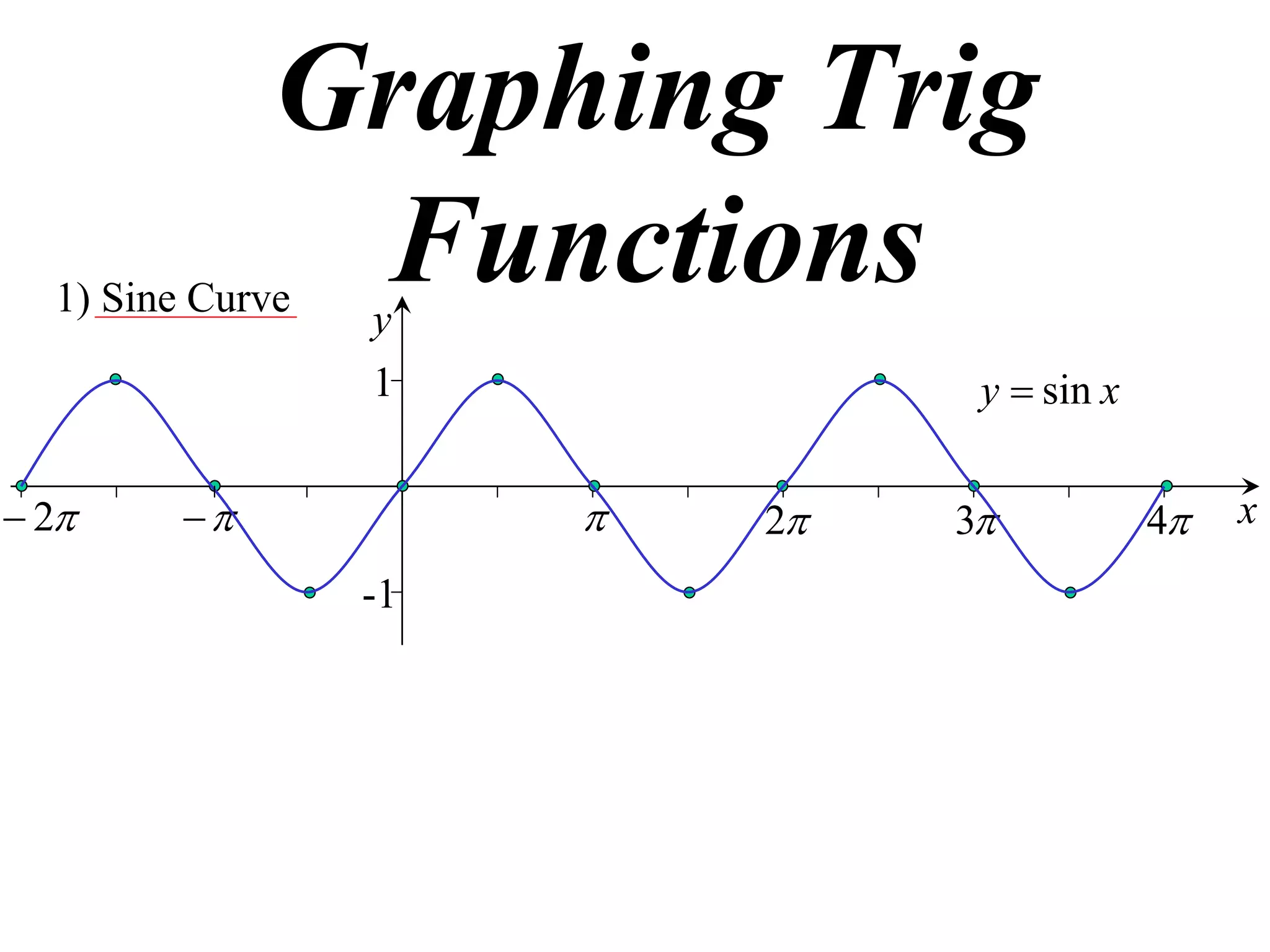
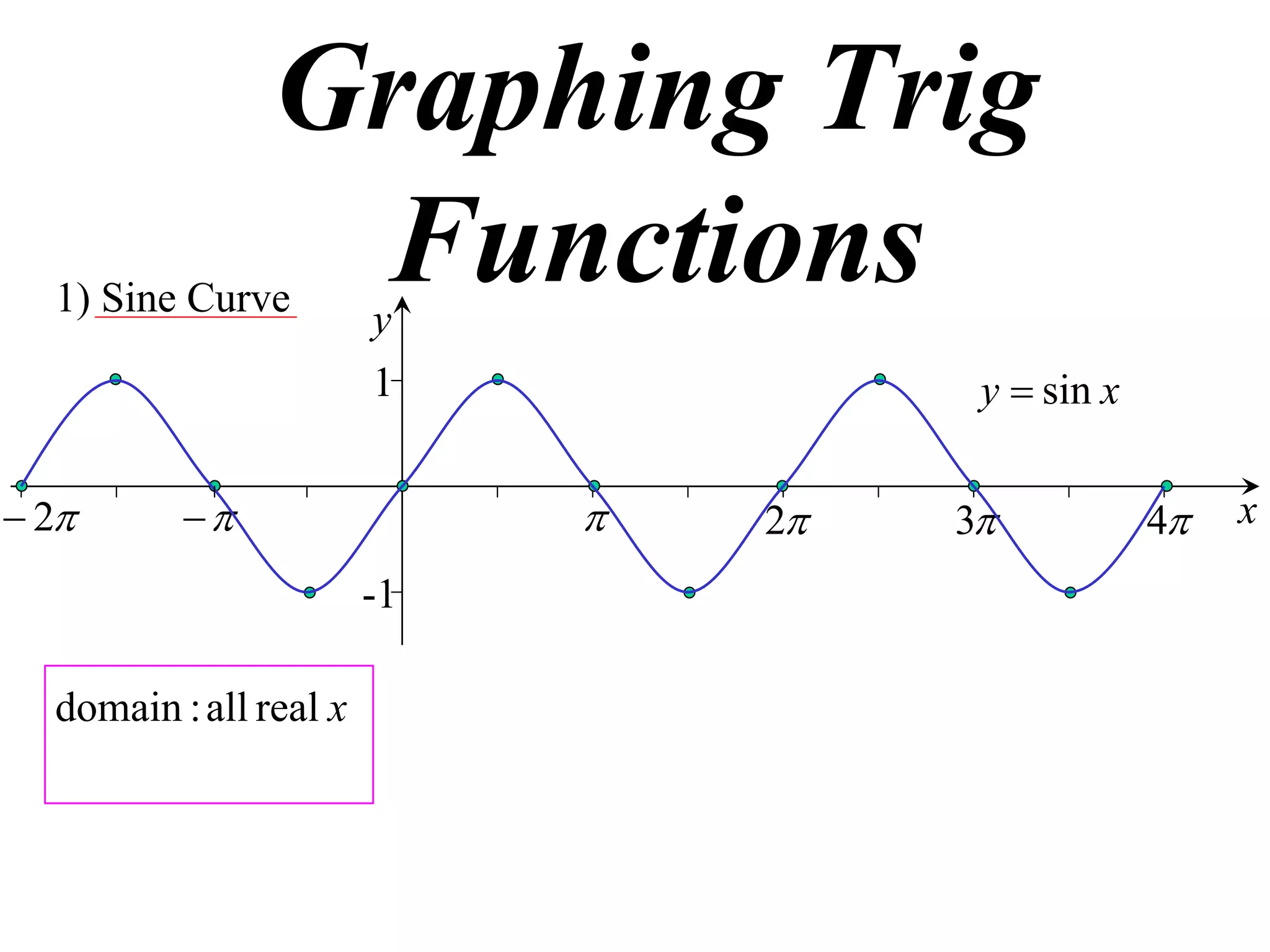
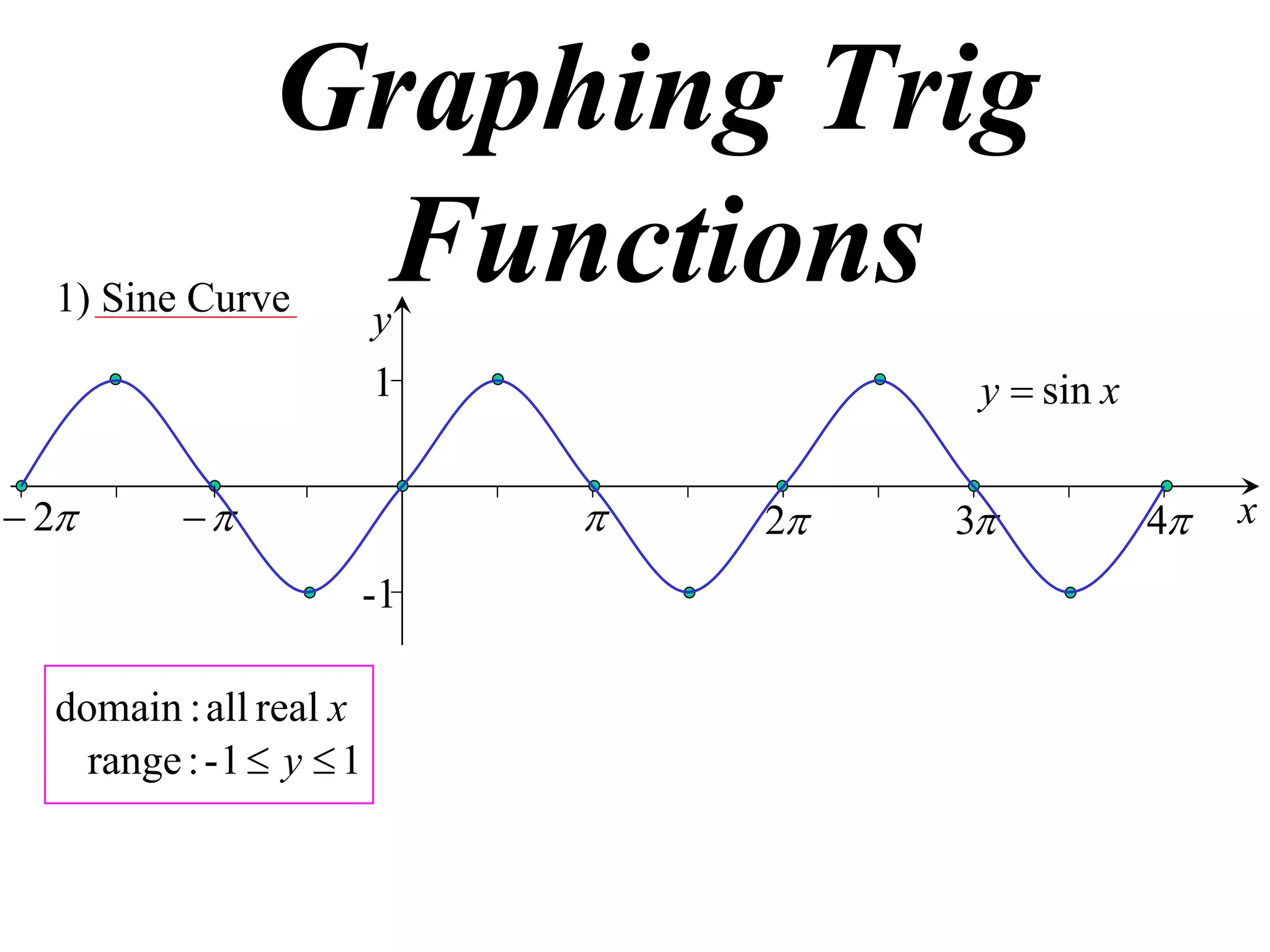
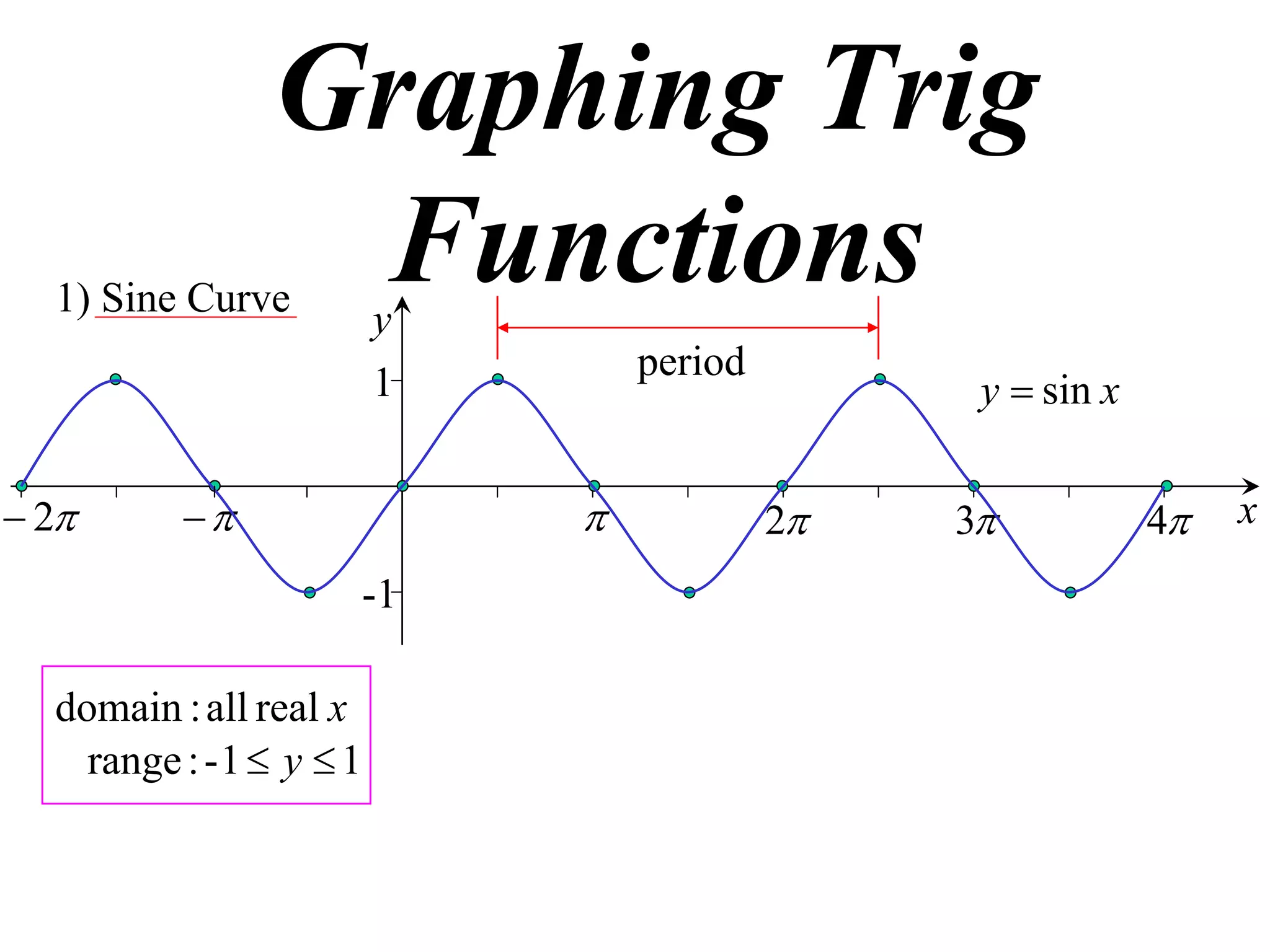
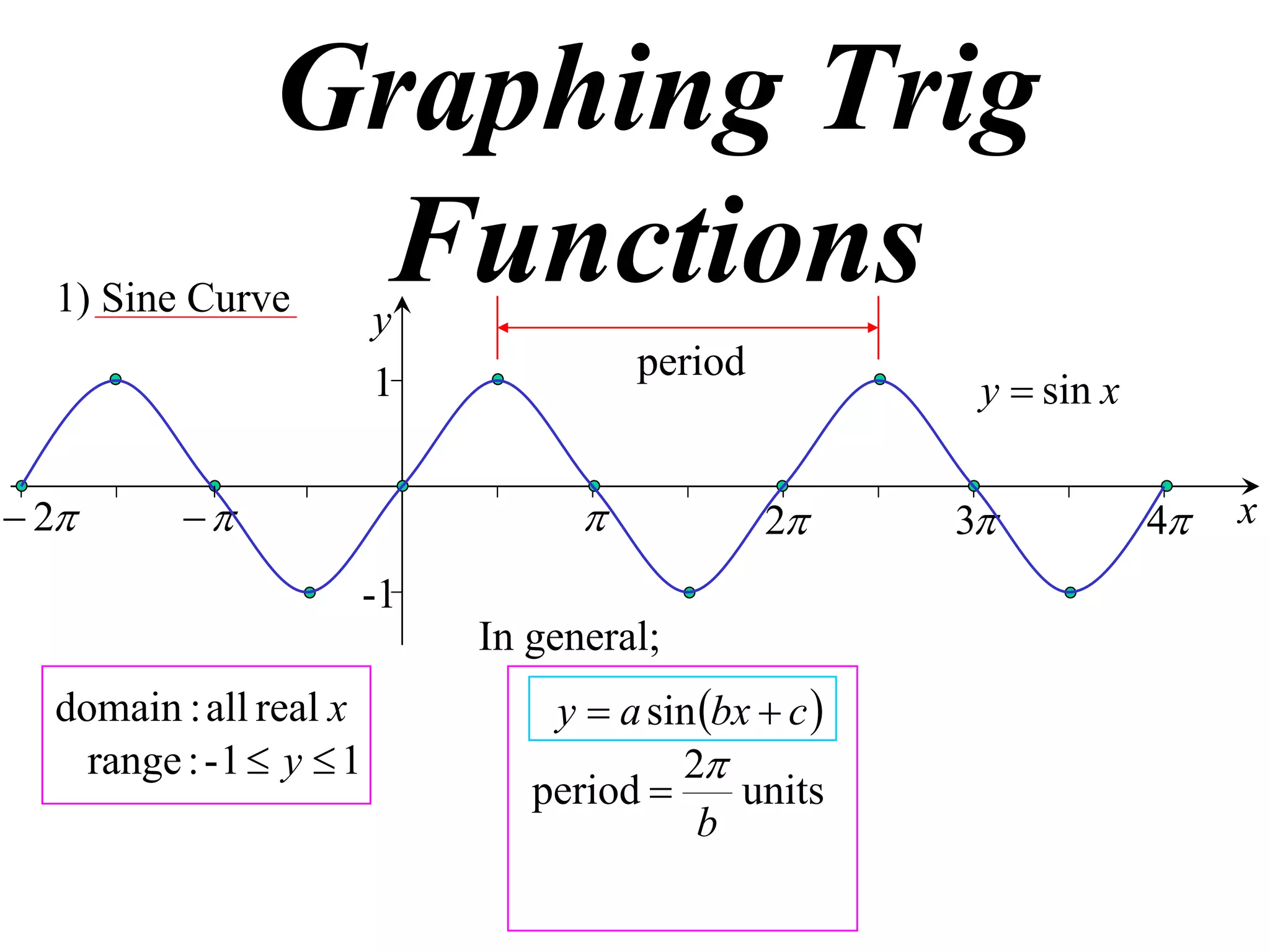
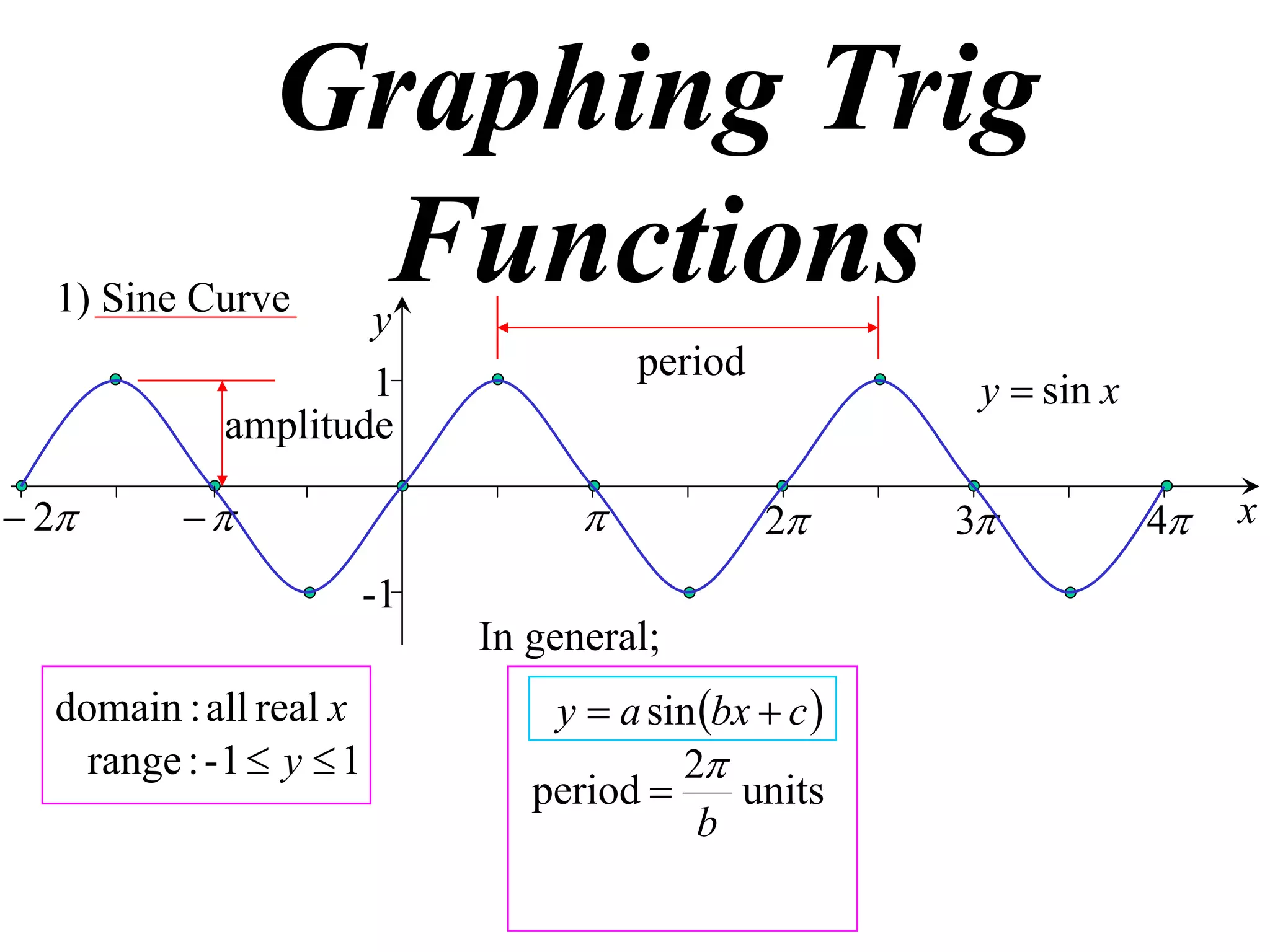
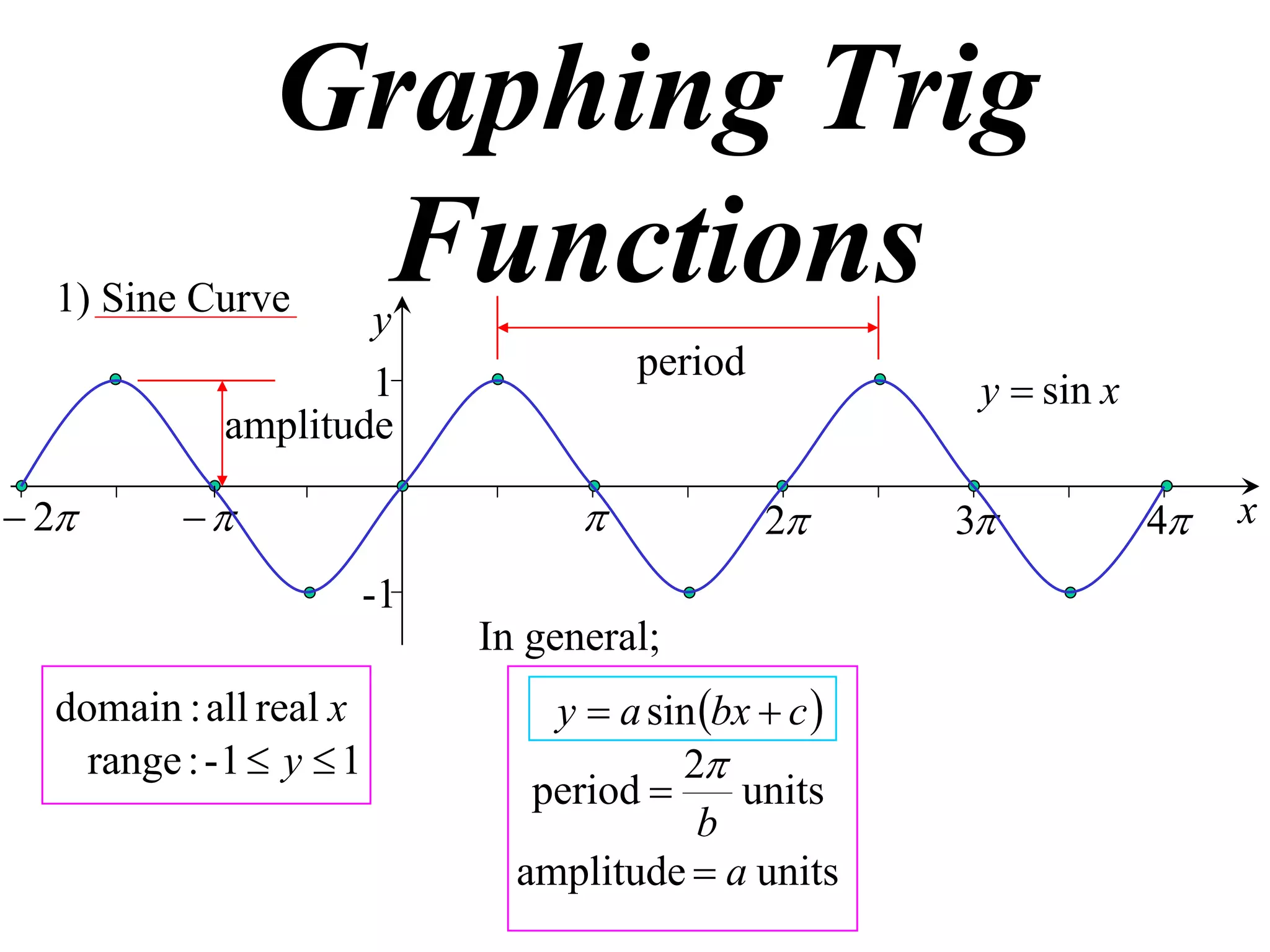
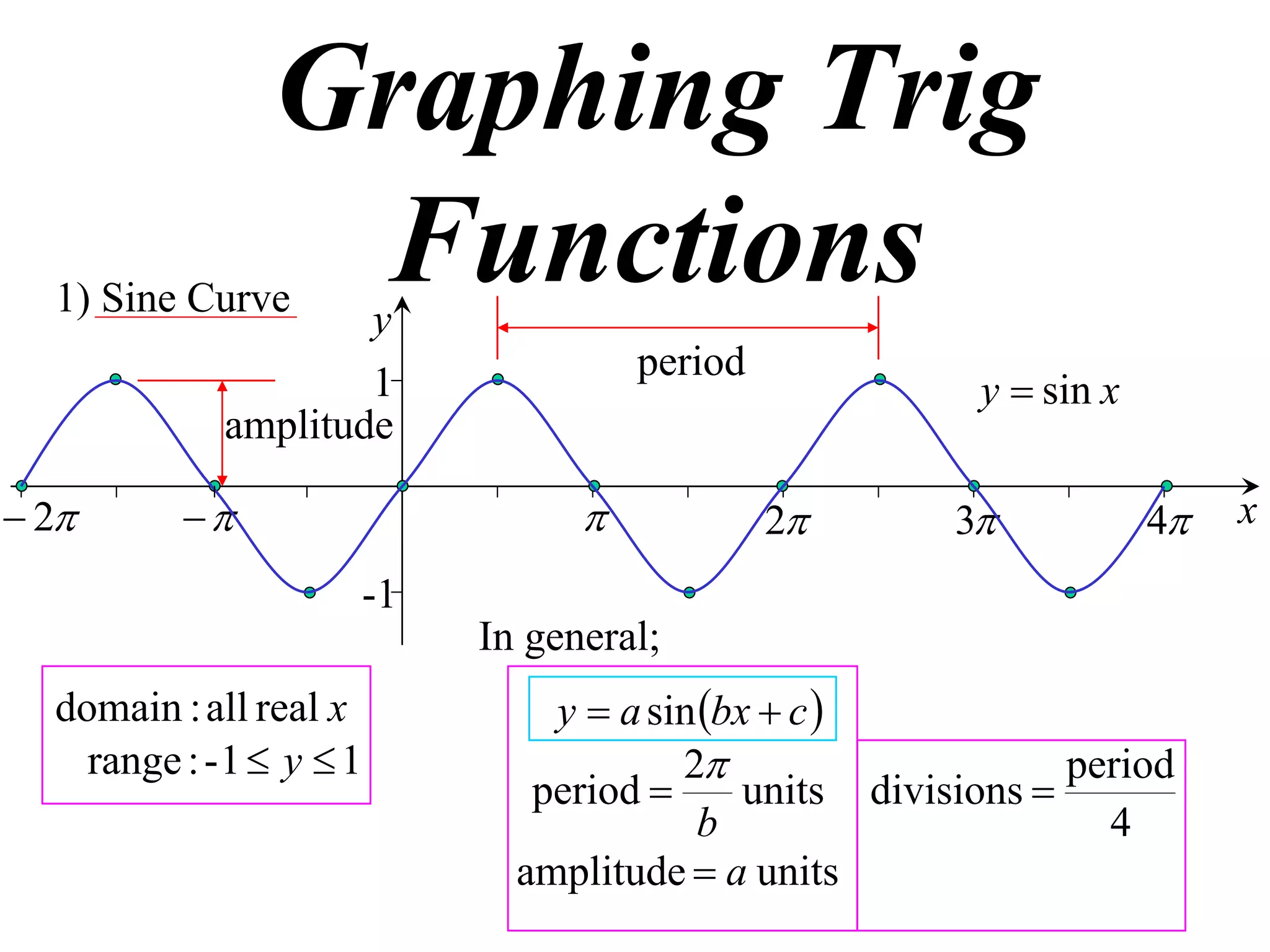
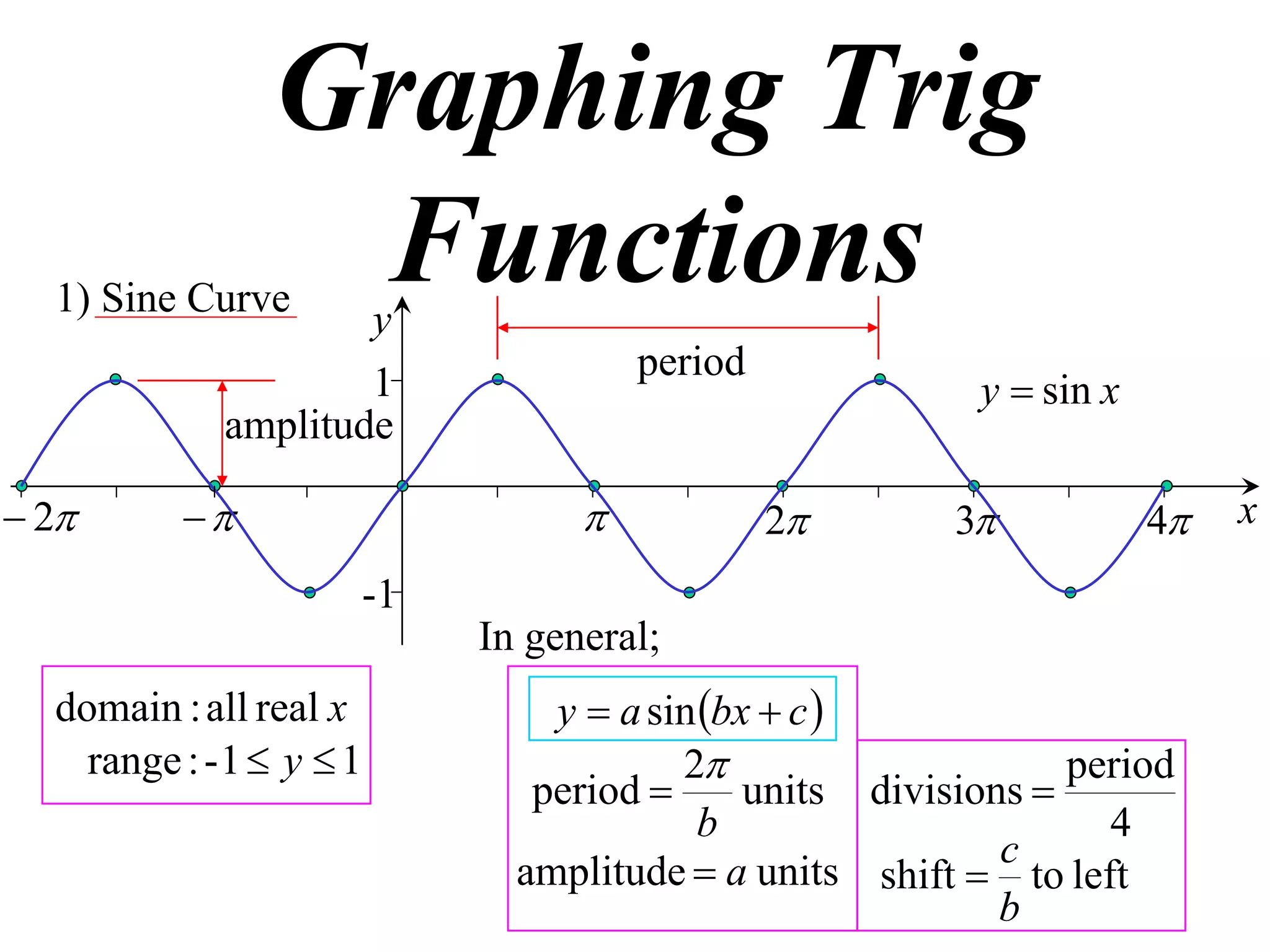
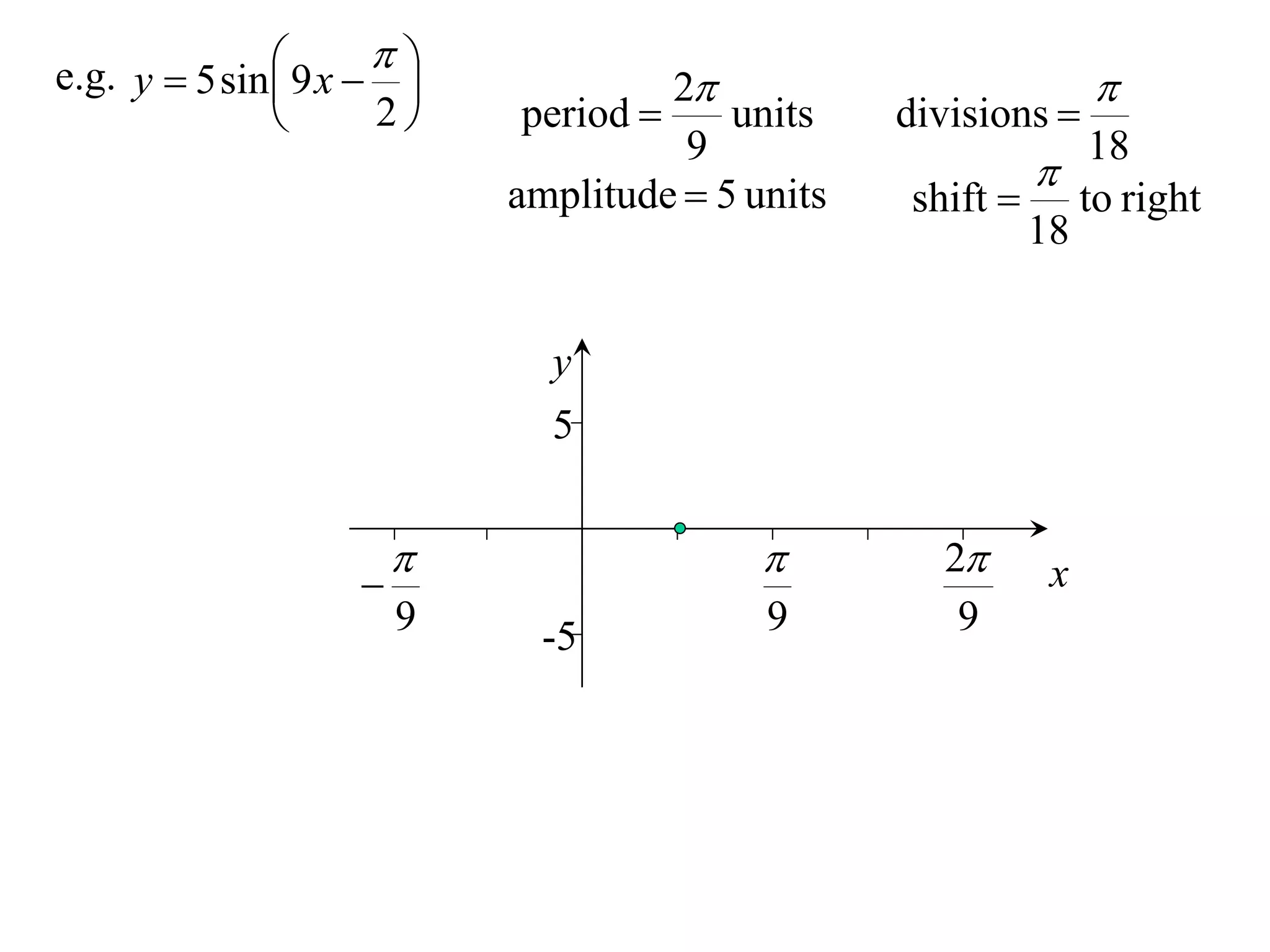
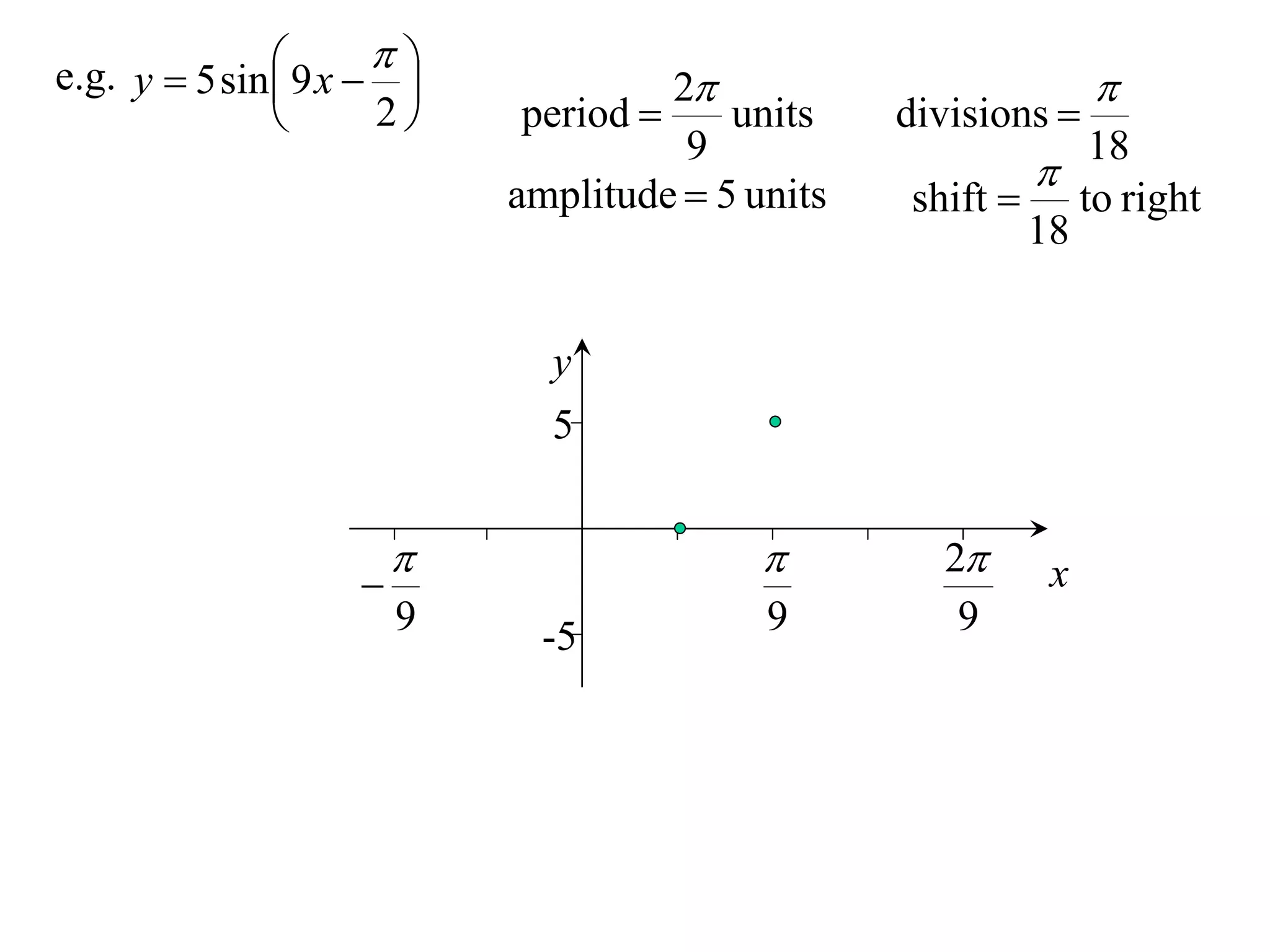
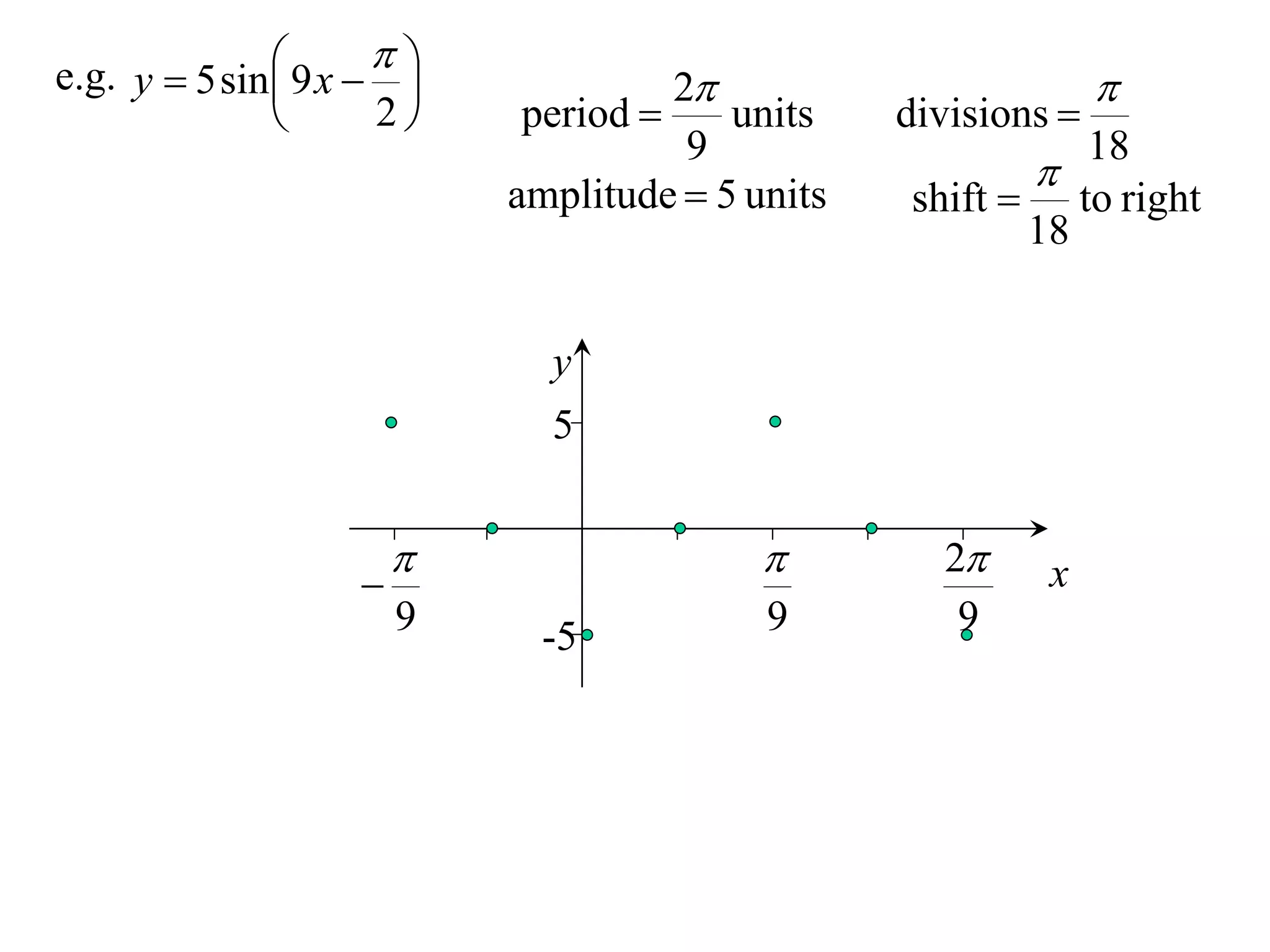
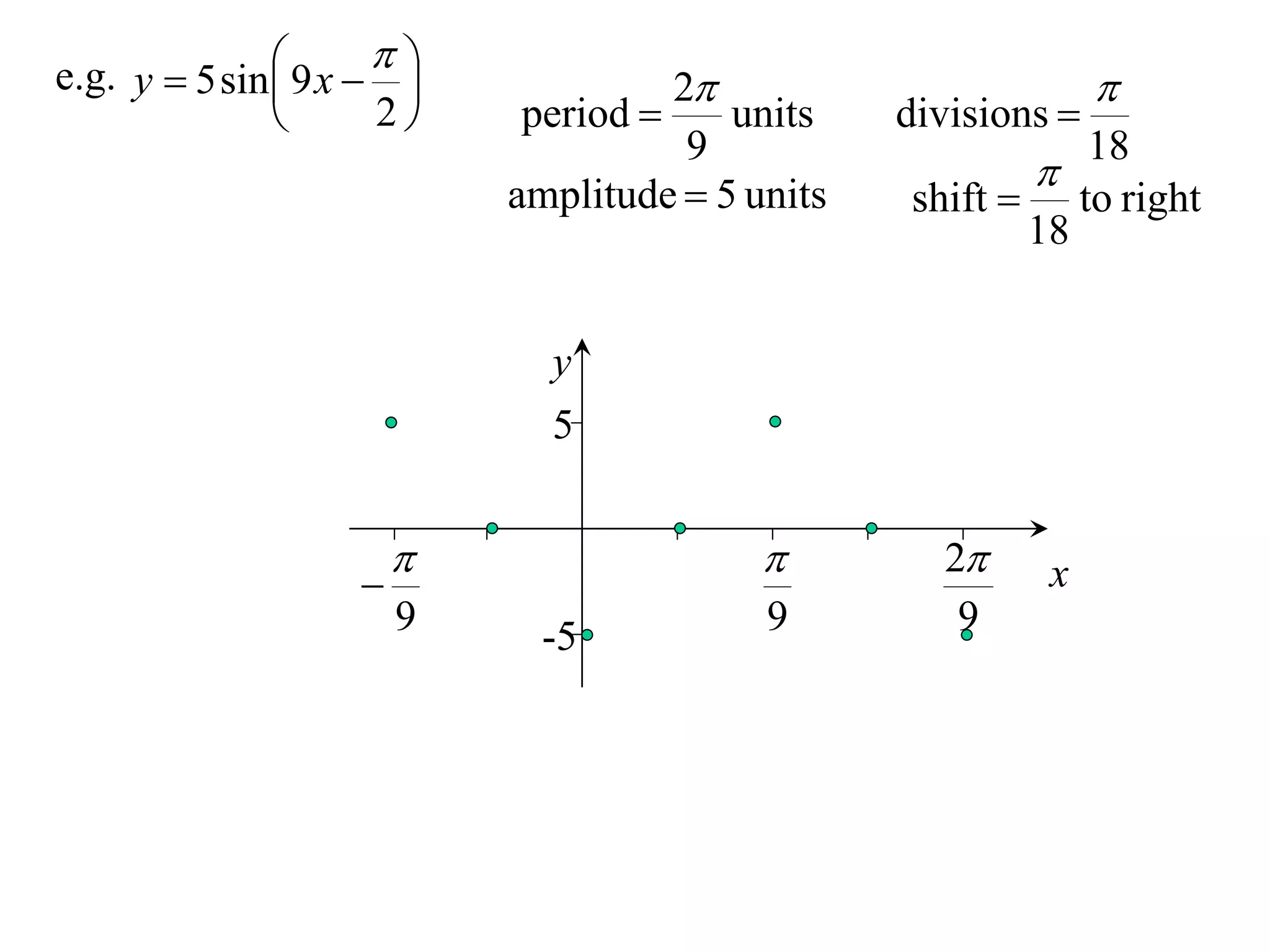
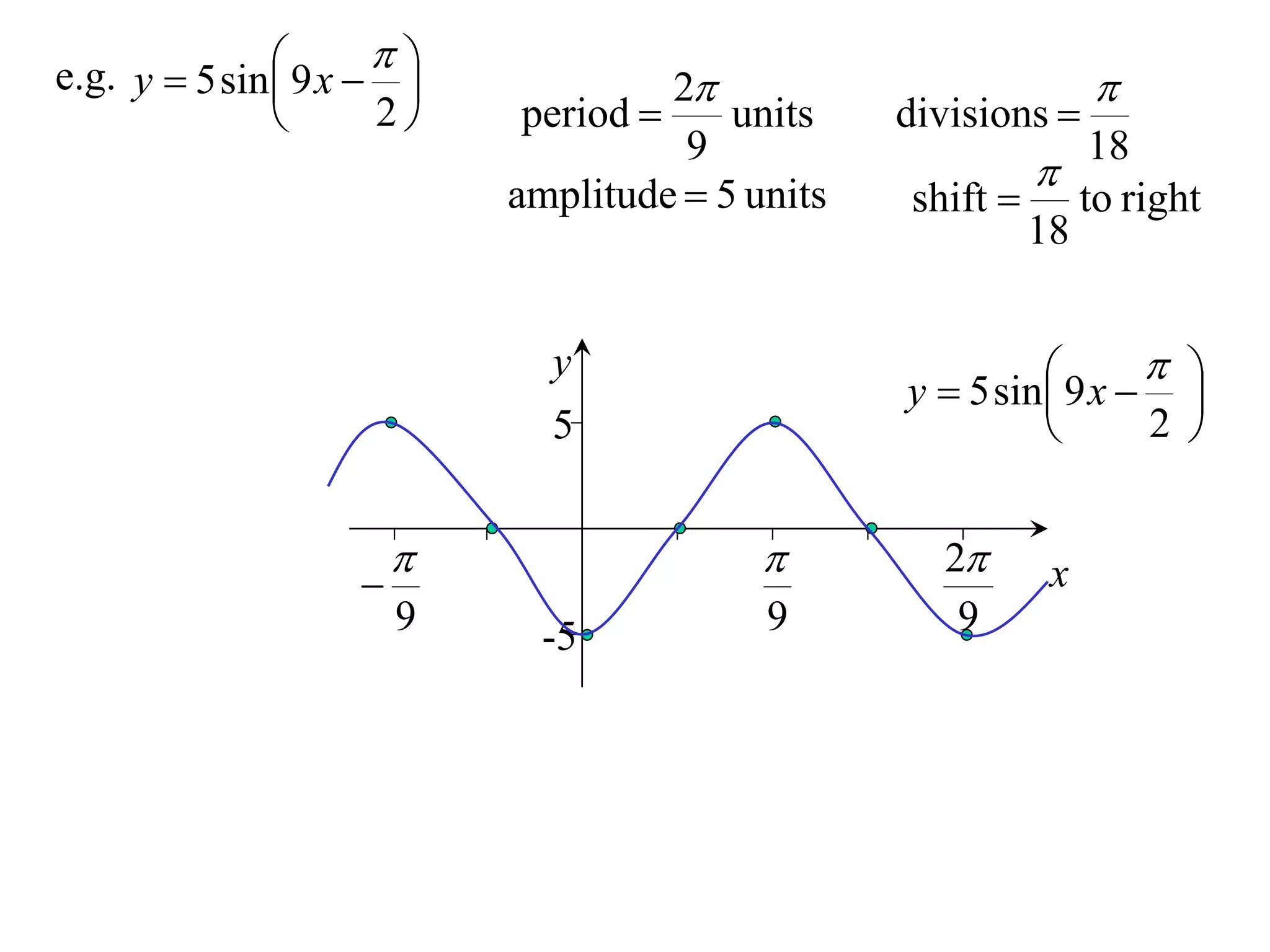
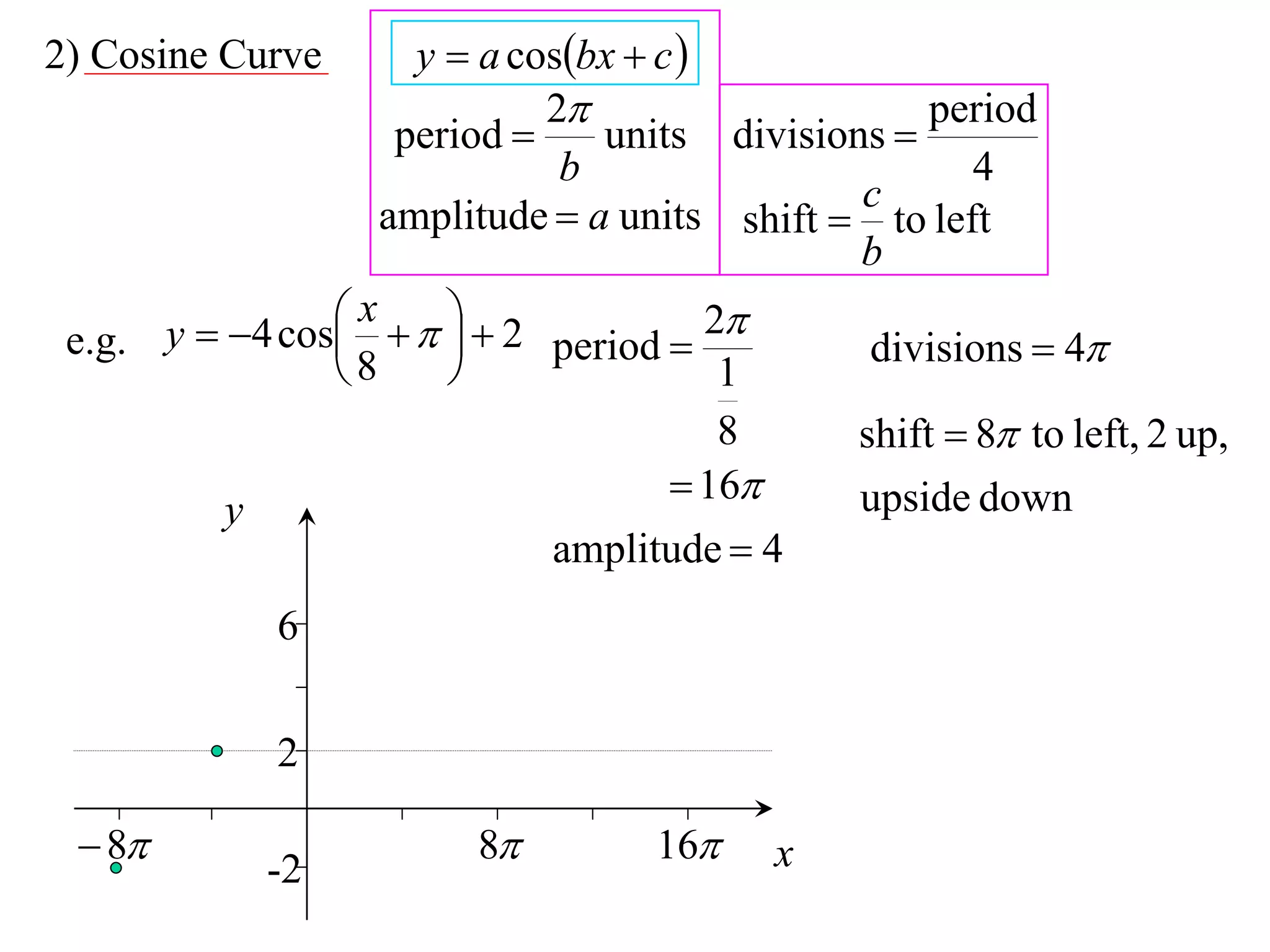
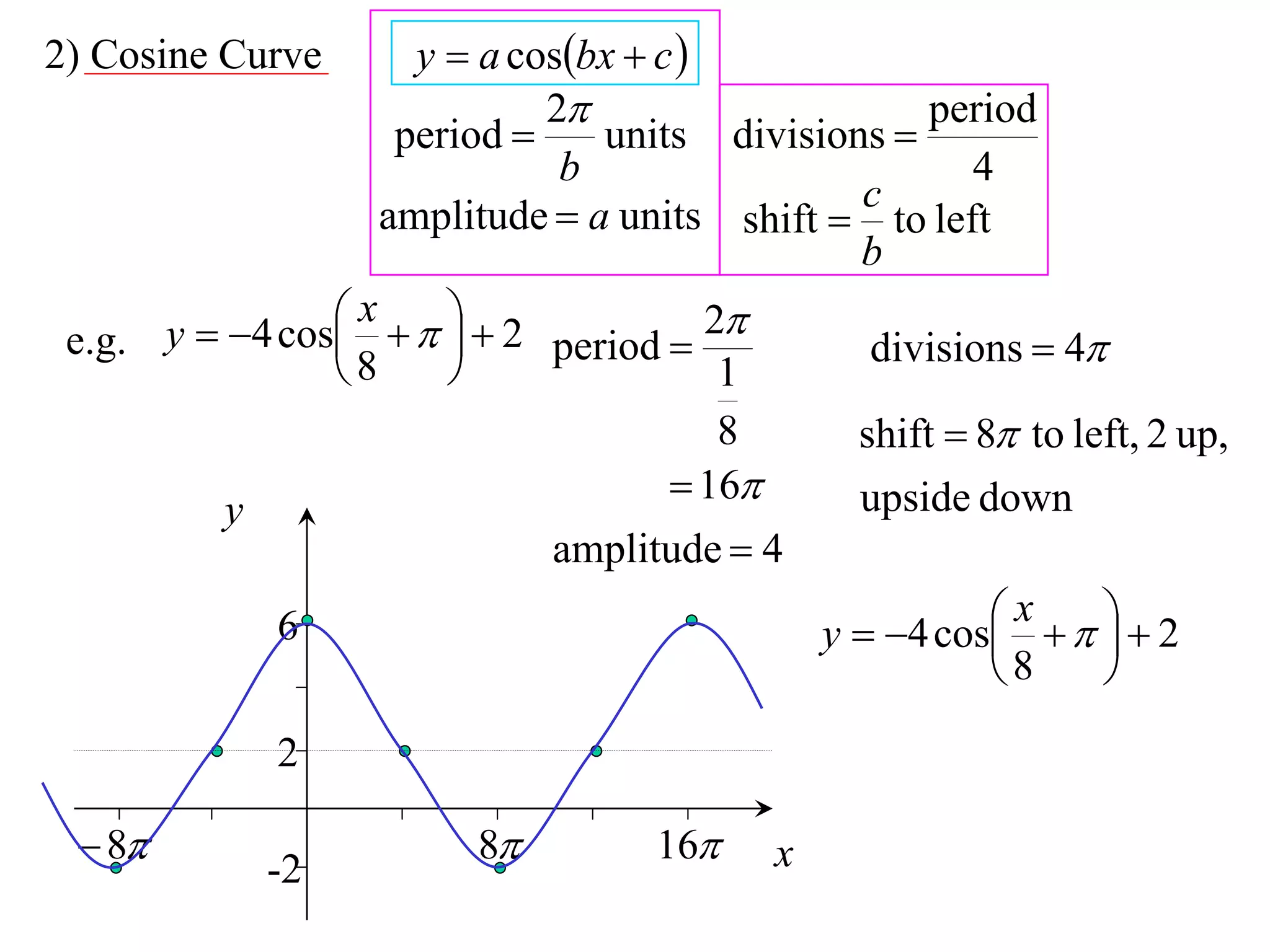
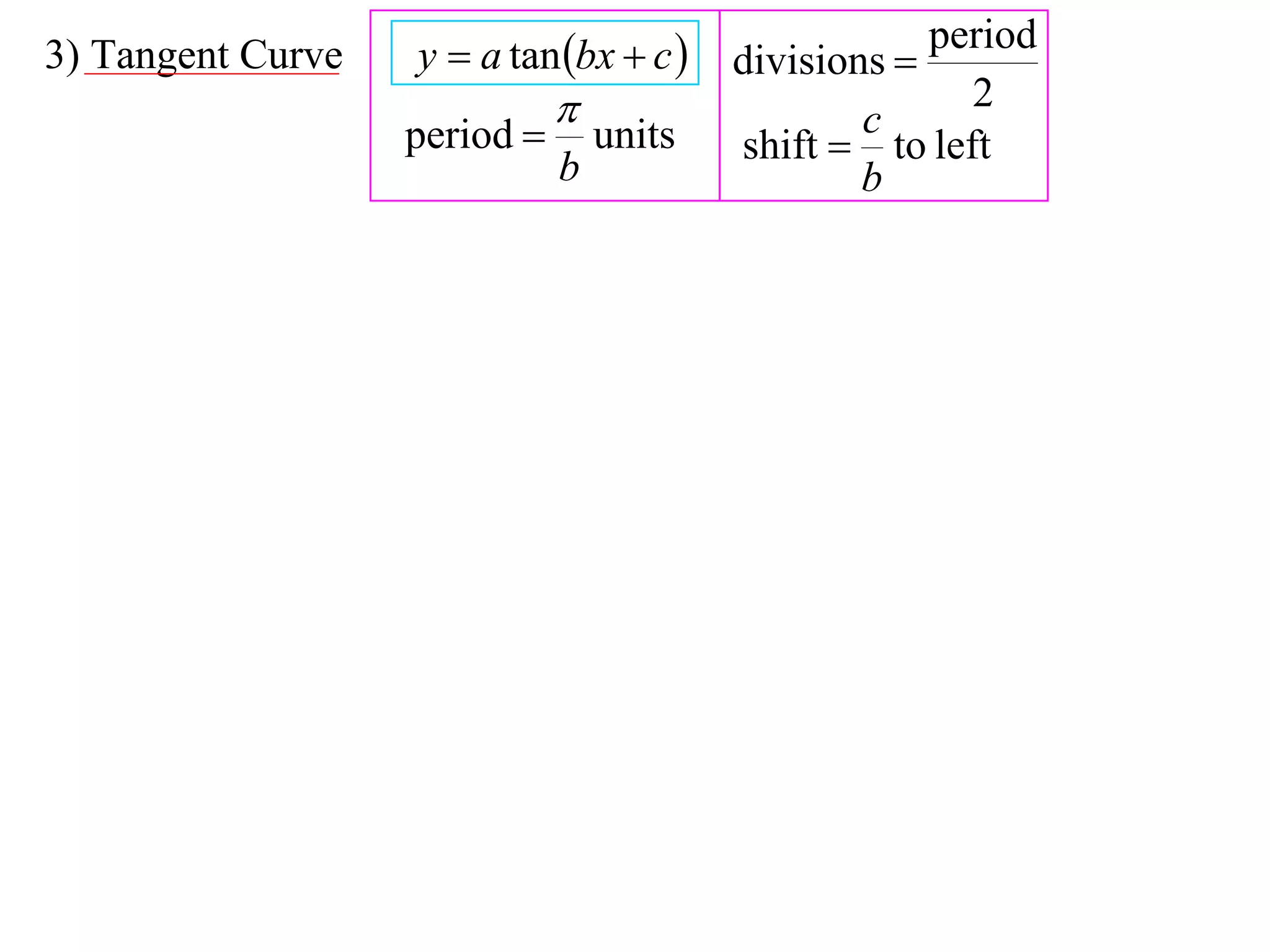
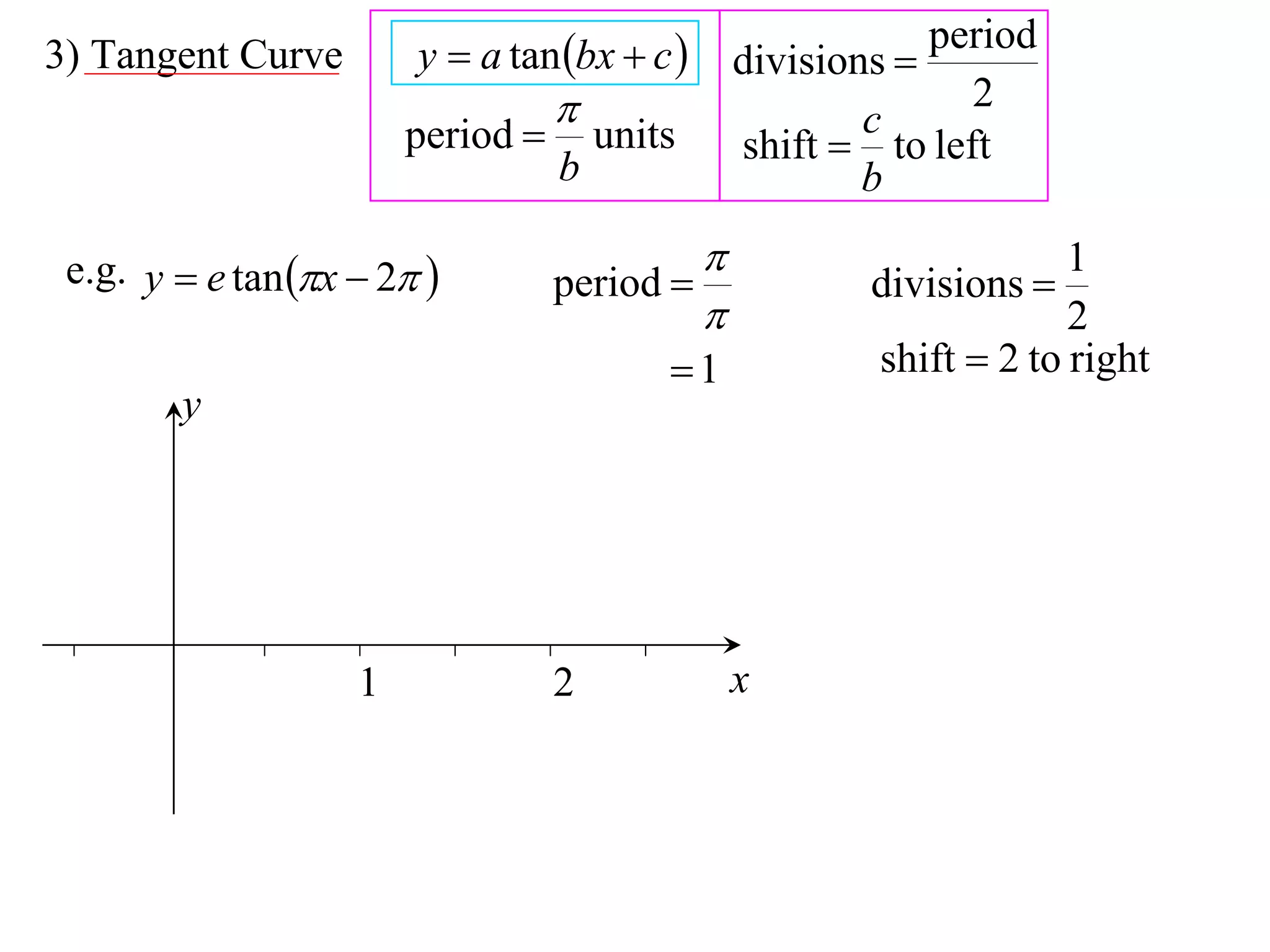
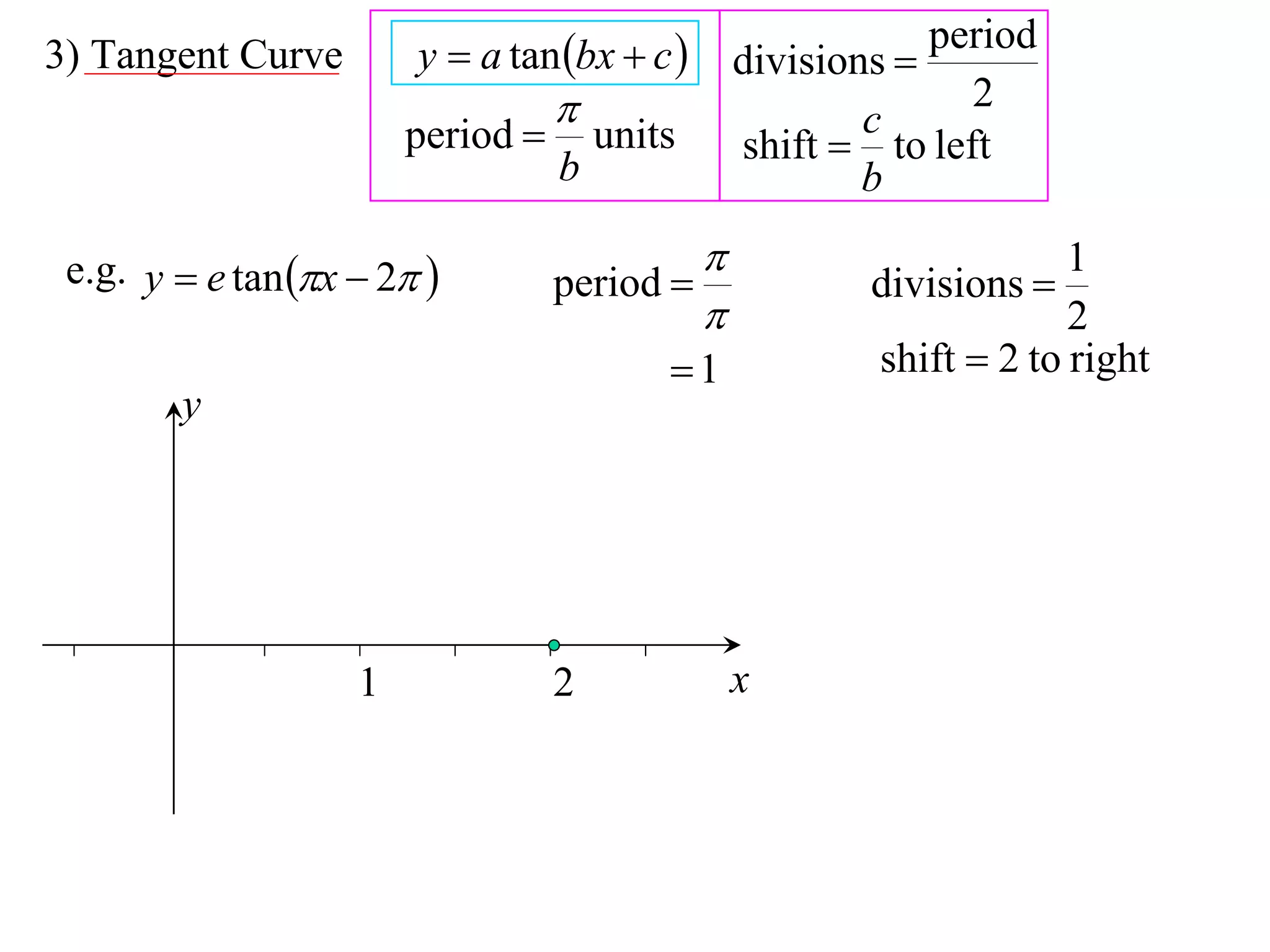
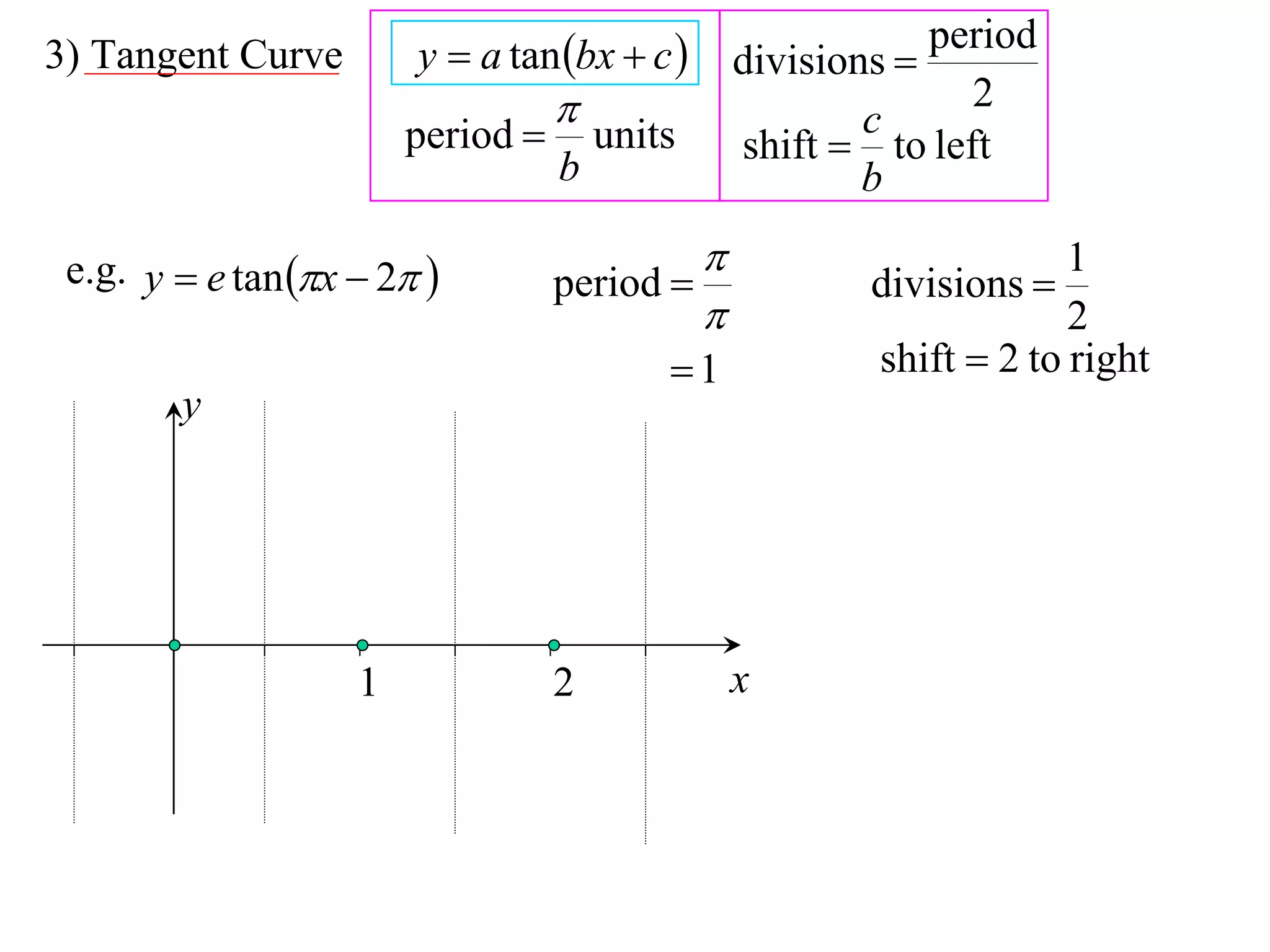
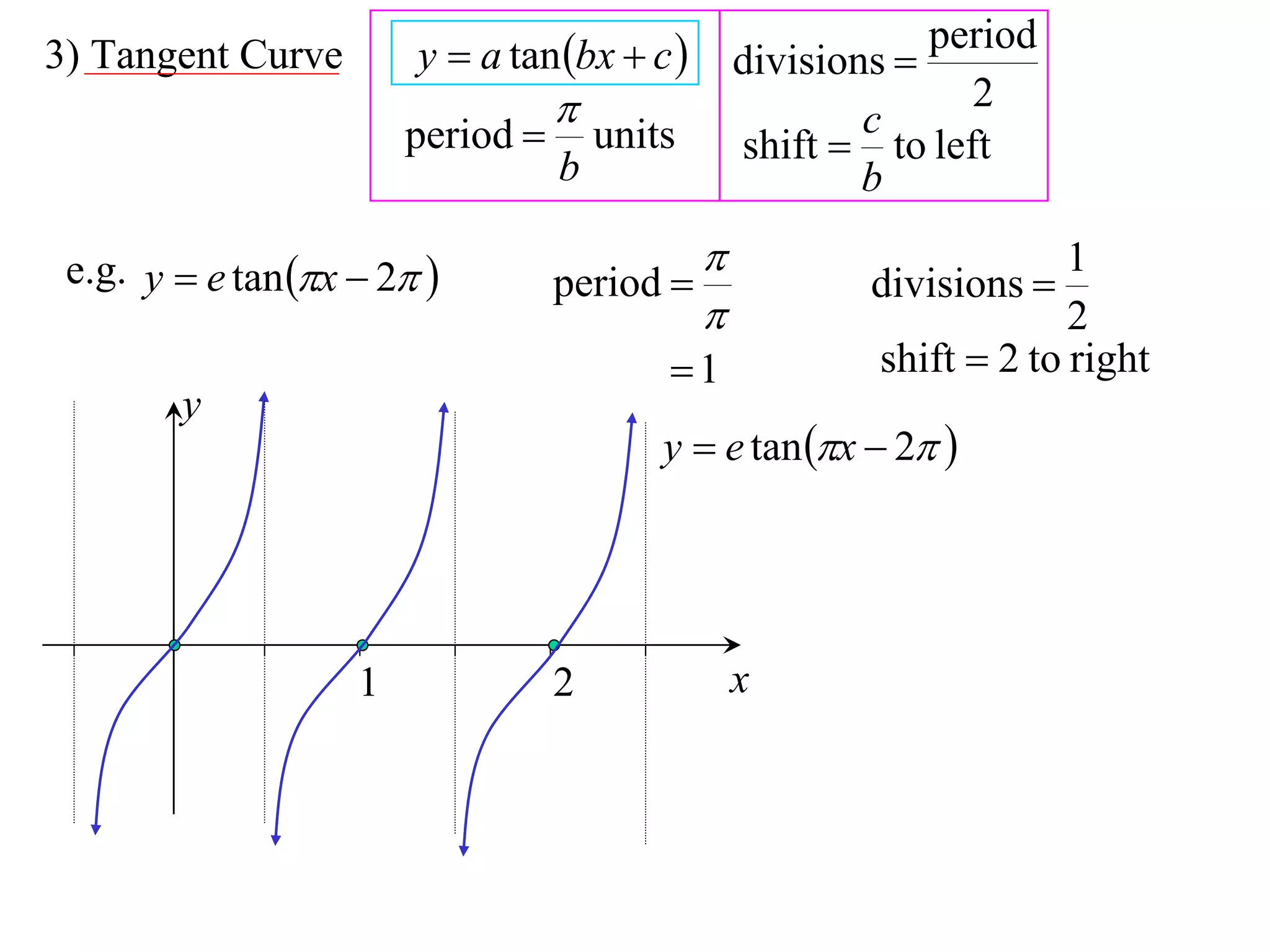
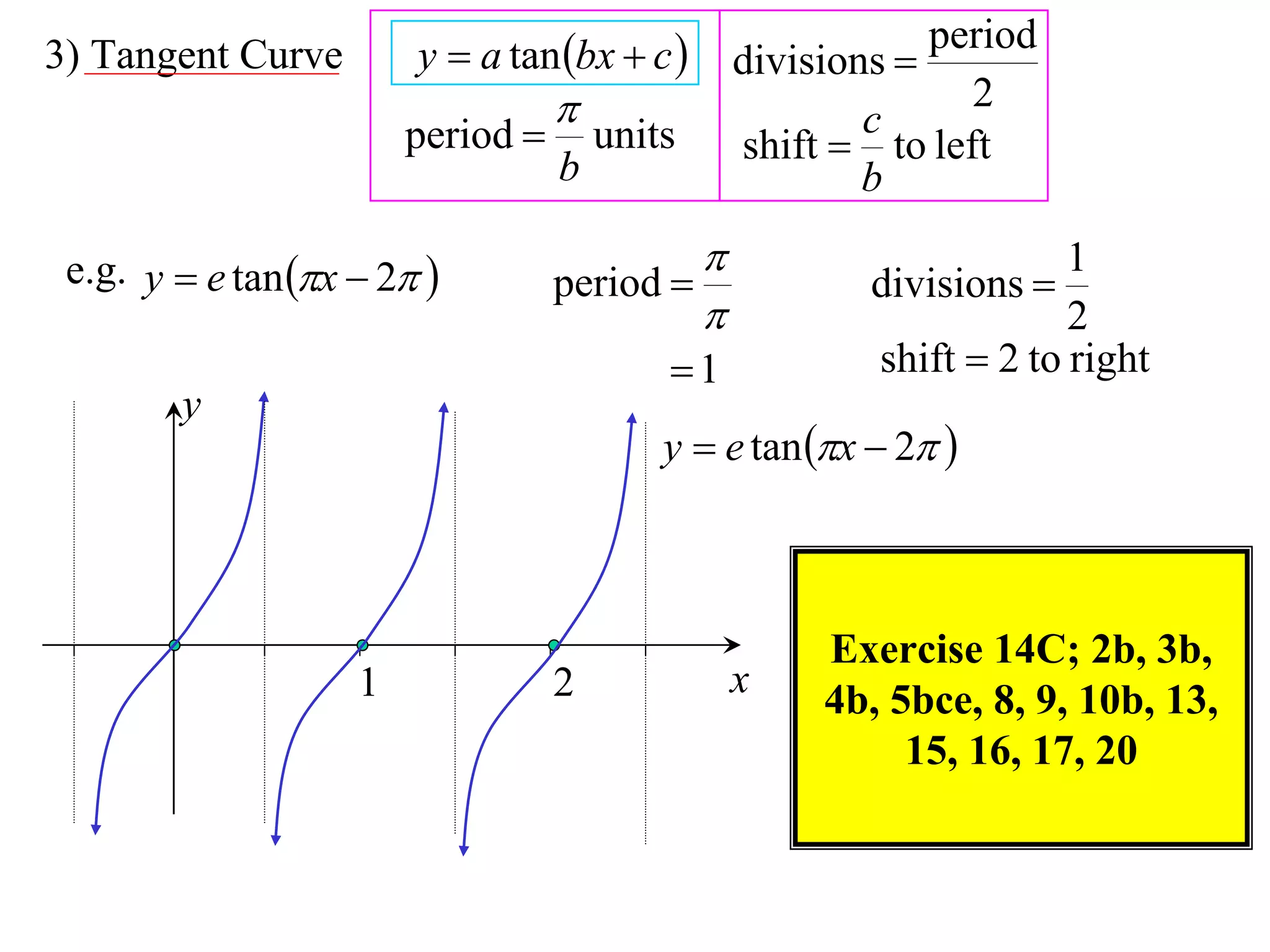
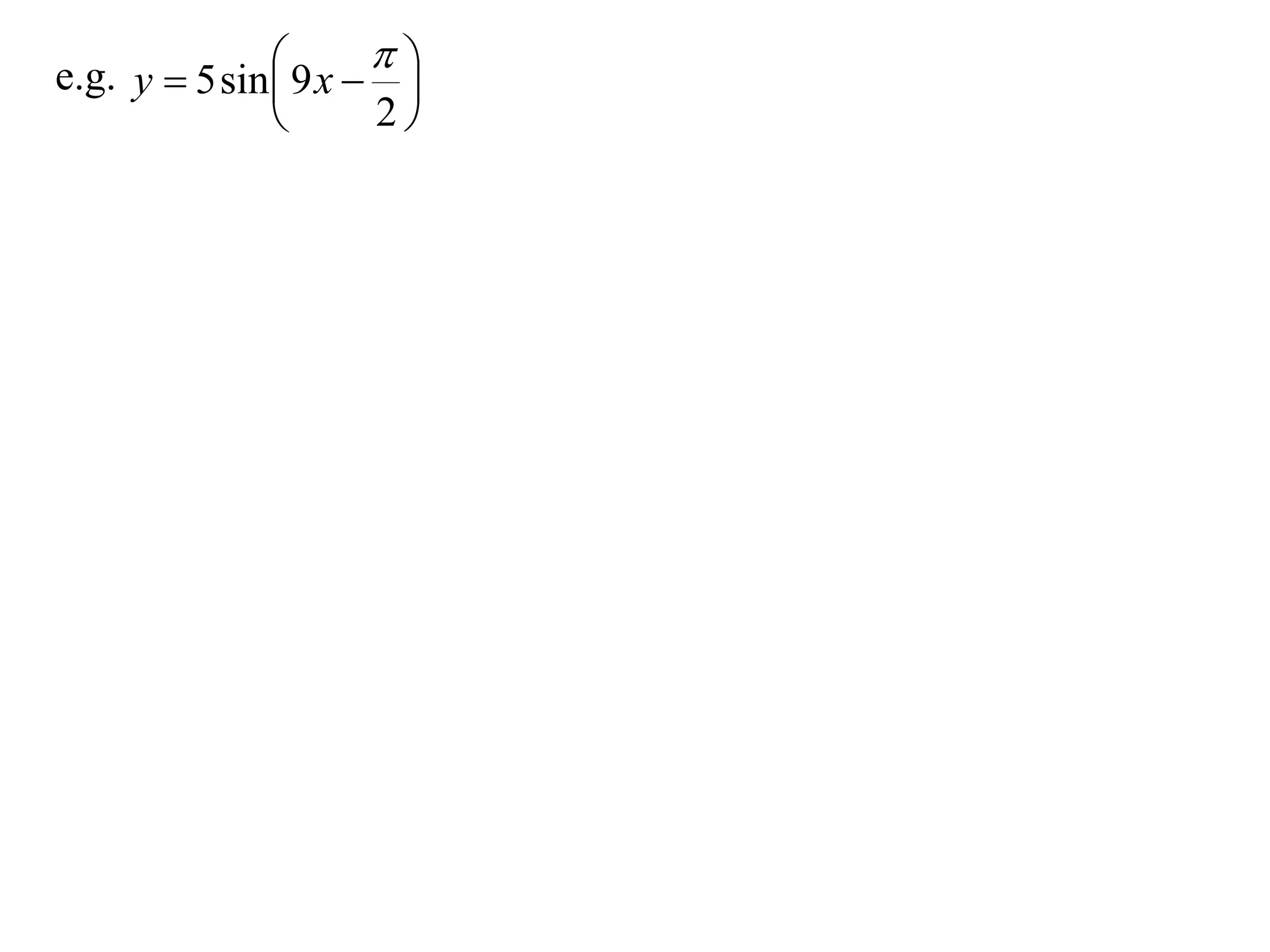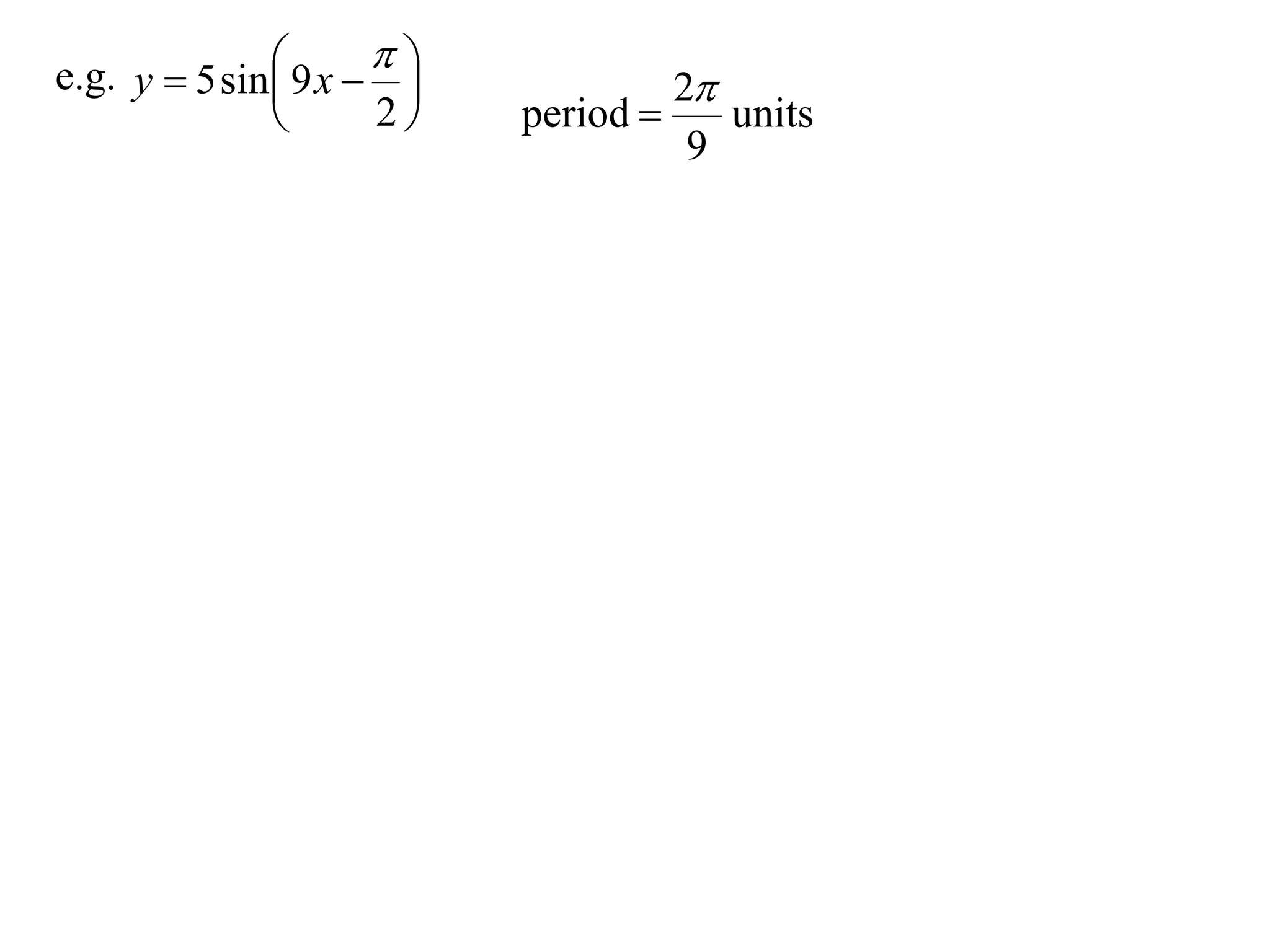The document discusses graphing trigonometric functions like sine and cosine curves. It explains that a sine curve is defined by the equation y = a sin(bx + c), where the period is 2π/b units, the amplitude is a units, and c shifts the curve left or right. A worked example graphs y = 5 sin(9x - π/2) with a period of 2π/9 units and amplitude of 5 units, shifted π/18 units to the right. The cosine curve is similarly defined by y = a cos(bx + c) with the same period, amplitude, and shift properties. An example graphs y = -4 cos((x + π)/8 + 2

1. Graphing Trig
Functions

2. Graphing Trig
1) Sine Curve
Functions

3. Graphing Trig
1) Sine Curve
Functions
y
1
-1

4. Graphing Trig
1) Sine Curve
Functions
y
1
 2   2 3 4 x
-1

5. Graphing Trig
1) Sine Curve
Functions
y
1
 2   2 3 4 x
-1

6. Graphing Trig
1) Sine Curve
Functions
y
1
 2   2 3 4 x
-1

7. Graphing Trig
1) Sine Curve
Functions
y
1
 2   2 3 4 x
-1

8. Graphing Trig
1) Sine Curve
Functions
y
1 y  sin x
 2   2 3 4 x
-1

9. Graphing Trig
1) Sine Curve
Functions
y
1 y  sin x
 2   2 3 4 x
-1
domain : all real x

10. Graphing Trig
1) Sine Curve
Functionsy
1 y  sin x
 2   2 3 4 x
-1
domain : all real x
range : - 1  y  1

11. Graphing Trig
1) Sine Curve
Functionsy
period
1 y  sin x
 2   2 3 4 x
-1
domain : all real x
range : - 1  y  1

12. Graphing Trig
1) Sine Curve
Functionsy
period
1 y  sin x
 2   2 3 4 x
-1
In general;
domain : all real x y  a sin bx  c 
range : - 1  y  1 2
period  units
b

13. Graphing Trig
1) Sine Curve
Functions
y
period
1 y  sin x
amplitude
 2   2 3 4 x
-1
In general;
domain : all real x y  a sin bx  c 
range : - 1  y  1 2
period  units
b

14. Graphing Trig
1) Sine Curve
Functions
y
period
1 y  sin x
amplitude
 2   2 3 4 x
-1
In general;
domain : all real x y  a sin bx  c 
range : - 1  y  1 2
period  units
b
amplitude  a units

15. Graphing Trig
1) Sine Curve
Functions
y
period
1 y  sin x
amplitude
 2   2 3 4 x
-1
In general;
domain : all real x y  a sin bx  c 
range : - 1  y  1 2 period
period  units divisions 
b 4
amplitude  a units

16. Graphing Trig
1) Sine Curve
Functions
y
period
1 y  sin x
amplitude
 2   2 3 4 x
-1
In general;
domain : all real x y  a sin bx  c 
range : - 1  y  1 2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b

17. 
e.g. y  5 sin  9 x  
 
 2

18. 
e.g. y  5 sin  9 x  
  2
 2 period  units
9

19. 
e.g. y  5 sin  9 x  
  2
 2 period  units
9
amplitude  5 units

20. 
e.g. y  5 sin  9 x  
  2 
 2 period  units divisions 
9 18
amplitude  5 units

21. 
e.g. y  5 sin  9 x  
  2 
 2 period  units divisions 
9 18

amplitude  5 units shift  to right
18

22. 
e.g. y  5 sin  9 x  
  2 
 2 period  units divisions 
9 18

amplitude  5 units shift  to right
18
y
5
  2
 x
9 -5 9 9

23. 
e.g. y  5 sin  9 x  
  2 
 2 period  units divisions 
9 18

amplitude  5 units shift  to right
18
y
5
  2
 x
9 -5 9 9

24. 
e.g. y  5 sin  9 x  
  2 
 2 period  units divisions 
9 18

amplitude  5 units shift  to right
18
y
5
  2
 x
9 -5 9 9

25. 
e.g. y  5 sin  9 x  
  2 
 2 period  units divisions 
9 18

amplitude  5 units shift  to right
18
y
5
  2
 x
9 -5 9 9

26. 
e.g. y  5 sin  9 x  
  2 
 2 period  units divisions 
9 18

amplitude  5 units shift  to right
18
y
5
  2
 x
9 -5 9 9

27. 
e.g. y  5 sin  9 x  
  2 
 2 period  units divisions 
9 18

amplitude  5 units shift  to right
18
y  9x   
y  5 sin  
5  2 
  2
 x
9 -5 9 9

28. 2) Cosine Curve

29. 2) Cosine Curve y  a cosbx  c 

30. 2) Cosine Curve y  a cosbx  c 
2
period  units
b

31. 2) Cosine Curve y  a cosbx  c 
2
period  units
b
amplitude  a units

32. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
amplitude  a units

33. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b

34. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2
e.g. y  4 cos 
 8 

35. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period 
8  1
8
 16

36. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period 
8  1
8
 16
amplitude  4

37. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period  divisions  4
8  1
8
 16
amplitude  4

38. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period  divisions  4
8  1
8 shift  8 to left, 2 up,
 16 upside down
amplitude  4

39. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period  divisions  4
8  1
8 shift  8 to left, 2 up,
 16 upside down
y
amplitude  4
6
2
 8 8 16 x
-2

40. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period  divisions  4
8  1
8 shift  8 to left, 2 up,
 16 upside down
y
amplitude  4
6
2
 8 8 16 x
-2

41. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period  divisions  4
8  1
8 shift  8 to left, 2 up,
 16 upside down
y
amplitude  4
6
2
 8 8 16 x
-2

42. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period  divisions  4
8  1
8 shift  8 to left, 2 up,
 16 upside down
y
amplitude  4
6
2
 8 8 16 x
-2

43. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period  divisions  4
8  1
8 shift  8 to left, 2 up,
 16 upside down
y
amplitude  4
6
2
 8 8 16 x
-2

44. 2) Cosine Curve y  a cosbx  c 
2 period
period  units divisions 
b 4
c
amplitude  a units shift  to left
b
 x    2 2
e.g. y  4 cos  period  divisions  4
8  1
8 shift  8 to left, 2 up,
 16 upside down
y
amplitude  4
y  4 cos     2

x
6 
8 
2
 8 8 16 x
-2

45. 3) Tangent Curve

46. 3) Tangent Curve y  a tan bx  c 

47. 3) Tangent Curve y  a tan bx  c 

period  units
b

48. 3) Tangent Curve y  a tan bx  c  divisions 
period
 2
period  units
b

49. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b

50. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2 

51. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2  
period 

1

52. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2   1
period  divisions 
 2
1

53. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2   1
period  divisions 
 2
1 shift  2 to right

54. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2   1
period  divisions 
 2
1 shift  2 to right
y
1 2 x

55. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2   1
period  divisions 
 2
1 shift  2 to right
y
1 2 x

56. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2   1
period  divisions 
 2
1 shift  2 to right
y
1 2 x

57. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2   1
period  divisions 
 2
1 shift  2 to right
y
y  e tan x  2 
1 2 x

58. 3) Tangent Curve y  a tan bx  c  divisions 
period
 c
2
period  units shift  to left
b b
e.g. y  e tan x  2   1
period  divisions 
 2
1 shift  2 to right
y
y  e tan x  2 
Exercise 14C; 2b, 3b,
1 2 x 4b, 5bce, 8, 9, 10b, 13,
15, 16, 17, 20