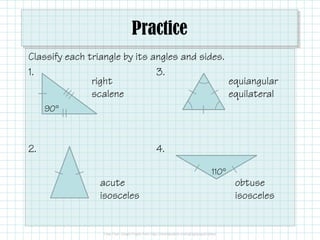
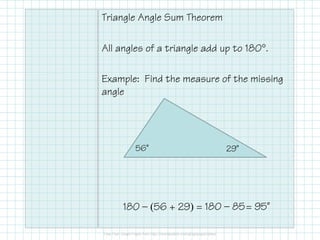
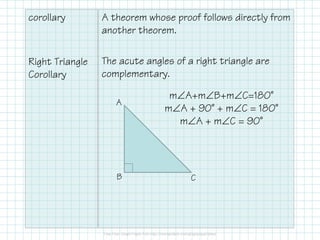
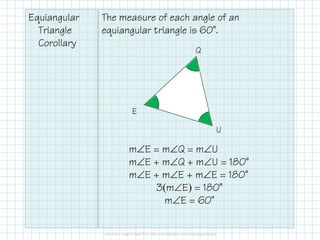
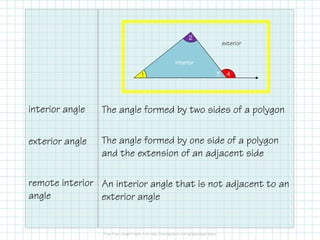
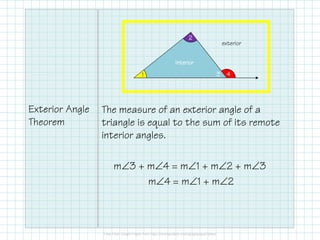
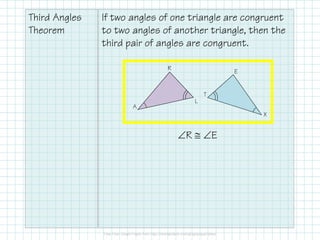
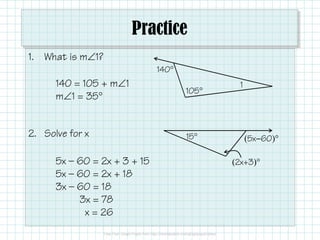
The document covers triangle classifications by side length (equilateral, isosceles, scalene) and angle measures (acute, right, obtuse, equiangular). It explains the triangle angle sum theorem and various corollaries related to right and equiangular triangles, as well as remote interior and exterior angles. The document also includes practice problems to find missing angles and to apply theorems related to triangle angles.

1. Triangle Angle Relationships
The student is able to (I can):
• Classify triangles by sides and by angles
• Find the measures of missing angles of right and• Find the measures of missing angles of right and
equiangular triangles
• Find the measures of missing remote interior and exterior
angles

2. Classifying Triangles
Recall that triangles are classified by their side lengths and
their angle measures as follows:
• By side length
— equilateral — all sides congruent (equal)
— isosceles — two or moreor moreor moreor more sides congruent— isosceles — two or moreor moreor moreor more sides congruent
— scalene — no sides congruent
• By angle measure
— acute — all acute angles
— right — one right angle
— obtuse — one obtuse angle
— equiangular — all angles congruent

3. Practice
Classify each triangle by its angles and sides.
1. 3.
90°
right
scalene
equiangular
equilateral
2. 4.
110°
acute
isosceles
obtuse
isosceles

4. Triangle Angle Sum Theorem
All angles of a triangle add up to 180°.
Example: Find the measure of the missing
angle
56˚ 29˚
180 — (56 + 29) = 180 — 85= 95˚

5. corollary
Right Triangle
Corollary
A theorem whose proof follows directly from
another theorem.
The acute angles of a right triangle are
complementary.
A
m∠A+m∠B+m∠C=180˚
m∠A + 90˚ + m∠C = 180˚
m∠A + m∠C = 90˚
B C
m∠A + m∠C = 90˚

6. Equiangular
Triangle
Corollary
The measure of each angle of an
equiangular triangle is 60˚.
E
Q
U
m∠E = m∠Q = m∠U
m∠E + m∠Q + m∠U = 180˚
m∠E + m∠E + m∠E = 180˚
3(m∠E) = 180˚
m∠E = 60˚

7. interior angle The angle formed by two sides of a polygon
1
2222
3333 4444
interiorinteriorinteriorinterior
exterior
exterior angle
remote interior
angle
The angle formed by one side of a polygon
and the extension of an adjacent side
An interior angle that is not adjacent to an
exterior angle

8. Exterior Angle
Theorem
The measure of an exterior angle of a
triangle is equal to the sum of its remote
1
2222
3333 4444
interiorinteriorinteriorinterior
exterior
Theorem triangle is equal to the sum of its remote
interior angles.
m∠3 + m∠4 = m∠1 + m∠2 + m∠3
m∠4 = m∠1 + m∠2

9. Third Angles
Theorem
If two angles of one triangle are congruent
to two angles of another triangle, then the
third pair of angles are congruent.
X
E
T
L
R
A
∠R ≅ ∠E

10. Practice
1. What is m∠1?
140°
105°
1140 = 105 + m∠1
m∠1 = 35°
2. Solve for x 15°
(2x+3)°
(5x‒60)°
5x — 60 = 2x + 3 + 15
5x — 60 = 2x + 18
3x — 60 = 18
3x = 78
x = 26