The document discusses multi-subject models of brain functional connectivity, including the use of statistical and generative models to account for subject variability in neuroimaging data. It explores methods such as Independent Component Analysis (ICA), multi-subject dictionary learning, and graphical models for analyzing brain connectivity and detecting differences in connectivity across groups. Additionally, it emphasizes the need for population-level models and proper statistical methods to improve diagnostic markers and understanding of brain function in various conditions.

1. Learning and comparing multi-subject models
of brain functional connectivity
Ga¨l Varoquaux
e INSERM/Unicog – INRIA/Parietal – Neurospin

2. Intrinsic brain structures in on-going activity?
(cognitive and systems neuroscience research)
Diagnostic markers in resting-state?
(medical applications)
Need population-level models
Statistical (generative) models
+ explicit subject variability
In order to
Accumulate data in a group
Compare subjects
G Varoquaux 2

3. Outline
1 Spatial modes of ongoing activity
2 Graphical models of brain connectivity
3 Detecting differences in connectivity
G Varoquaux 3

4. 1 Spatial modes of ongoing
activity
G Varoquaux 4

5. 1 Spatial modes of ongoing
activity
G Varoquaux 4

6. 1 Decomposing in spatial modes: a model
voxels voxels
voxels
Y E · S + N
time
time
time
=
25
Decomposing time series into:
covarying spatial maps, S
uncorrelated residuals, N
ICA: minimize mutual information across S
G Varoquaux 5

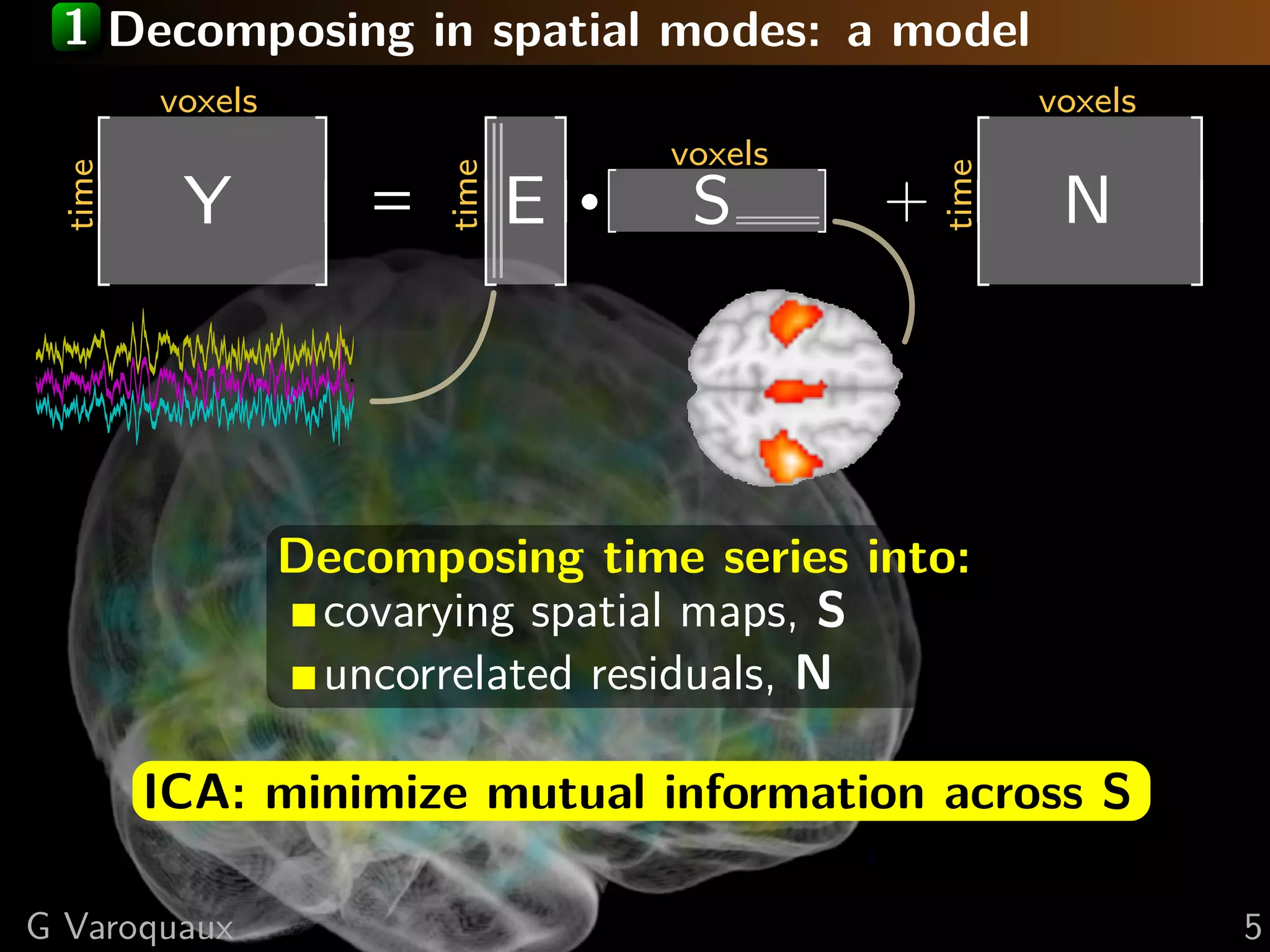
7. 1 ICA on multiple subjects: group ICA
Estimate common spatial maps S:
voxels voxels
voxels
Y
1
E
1
· S + N
1
time
time
time
=
·
· ·
· ·
·
s s s
Y E · S + N
time
time
time
=
G Varoquaux [Calhoun HBM 2001] 6

8. 1 ICA on multiple subjects: group ICA
Estimate common spatial maps S:
voxels voxels
voxels
Y
1
E
1
· S + N
1
time
time
time
=
·
· ·
· ·
·
s s s
Y E · S + N
time
time
time
=
Concatenate images, minimize norm of residuals
Corresponds to fixed-effects modeling:
i.i.d. residuals Ns
G Varoquaux [Calhoun HBM 2001] 6

9. 1 ICA: Noise model
Observation noise: minimize group residuals (PCA):
voxels voxels
voxels
Y W · B + O
time
time
time
concat =
Learn interesting maps (ICA):
voxels voxels
·
sources
sources
B = M S
G Varoquaux 7

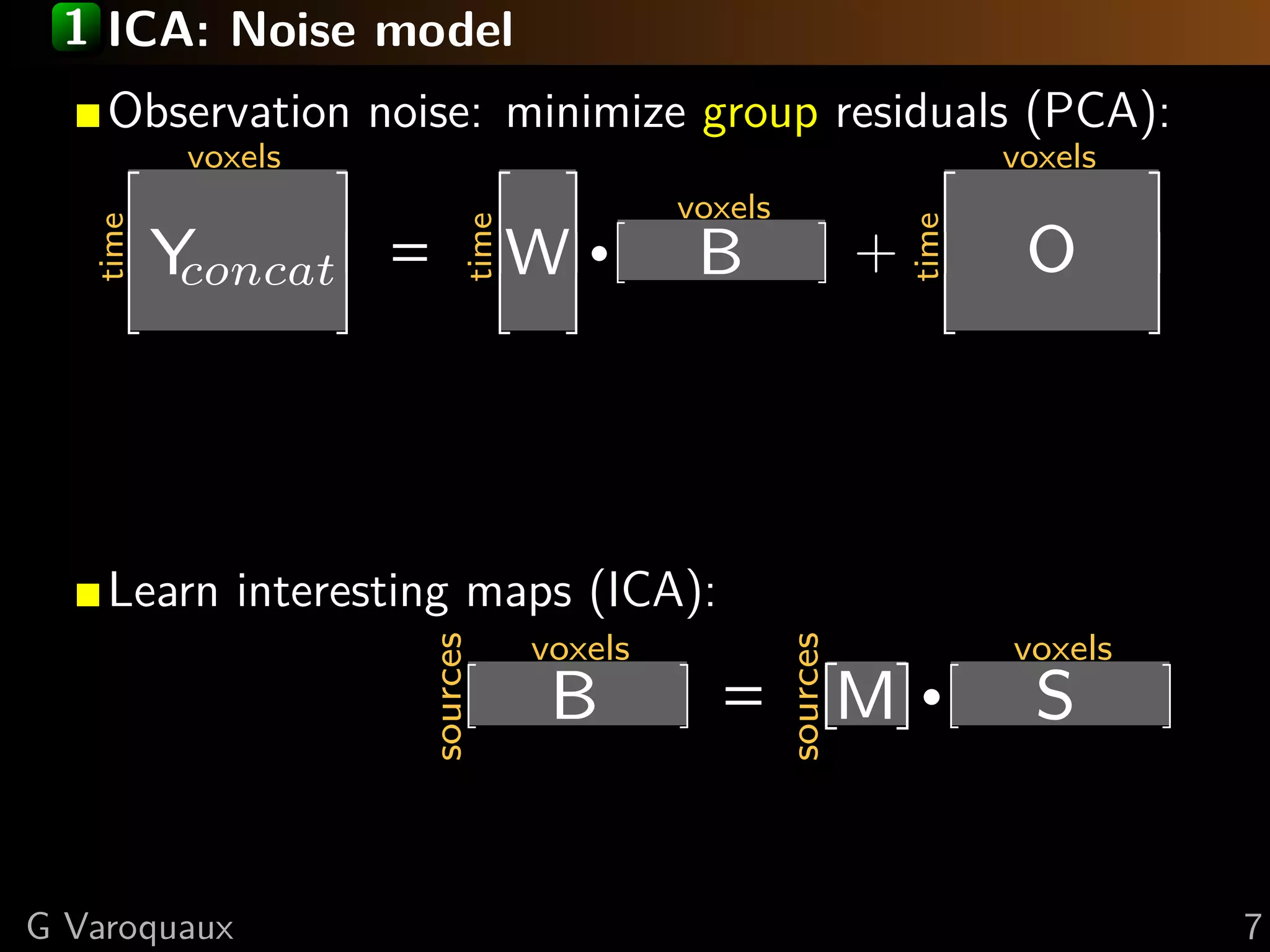
10. 1 CanICA: random effects model
Observation noise: minimize subject residuals (PCA):
voxels voxels
Subject
voxels
Y W · P + Os
time
time
time
s = s s
Select signal similar across subjects (CCA):
voxels
P1
Group
voxels
·
subjects
sources
.
.
. = Λ· B + R
Ps
Learn interesting maps (ICA):
voxels voxels
·
sources
sources
B = M S
G Varoquaux [Varoquaux NeuroImage 2010] 8

11. 1 CanICA: experimental validation
Reproducibility across controls groups
no CCA CanICA MELODIC
.36 (.02) .72 (.05) .51 (.04)
Qualitative observation: less ’noise’ components
G Varoquaux [Varoquaux NeuroImage 2010] 9

12. 1 Noise in the ICA maps
How to describe noise versus signal?
⇓ ⇓
Blobs standing out
Background noise
G Varoquaux [Varoquaux ISBI 2010] 10

13. 1 Noise in the ICA maps
How to describe noise versus signal?
Joint
distribution:
Blobs standing out = long-tailed distribution
Background noise = isotropic central mode
G Varoquaux [Varoquaux ISBI 2010] 10

14. 1 Noise in the ICA maps
How to describe noise versus signal?
⇓ ⇓
Thresholding
Joint
distribution:
G Varoquaux [Varoquaux ISBI 2010] 10

15. 1 ICA as a sparse decomposition
⇒
voxels
·( voxels voxels
(
sources
sources
B = M S + Q
Interesting sources S are sparse
Q: Gaussian noise
Thresholding ICA = sparse recovery
Experimental validation: on sub-sampled signal:
more robust than other approaches
G Varoquaux [Varoquaux ISBI 2010] 11

16. 1 The group-level ICA maps
Visual system
map 0, reproducibility: 0.54
-74
V1 0 9
map 1, reproducibility: 0.52
-91
V1-V2 3 -3
map 3, reproducibility: 0.47
-80 40 4
extrastriate
map 25, reproducibility: 0.34
-78 -30 24
superior parietal
G Varoquaux [Varoquaux NeuroImage 2010] 12

17. 1 The group-level ICA maps
Motor system
map 4, reproducibility: 0.47
part of
-25 -1 62
motor
map 21, reproducibility: 0.36
part of
-21 -42 54
motor
map 32, reproducibility: 0.30
part of
-8 -54 29
motor
G Varoquaux [Varoquaux NeuroImage 2010] 12

18. 1 The group-level ICA maps
Frontal structures
map 18, reproducibility: 0.37 map 23, reproducibility: 0.35
dorsal
43
frontal -30 28 10
medial wall
0 54
map 29, reproducibility: 0.31
21 pre-frontal 0 24
map 39, reproducibility: 0.26 map 37, reproducibility: 0.28
part of part of
21 prefronto-insular -34 -8 15 prefronto-insular -42 -3
G Varoquaux [Varoquaux NeuroImage 2010] 12

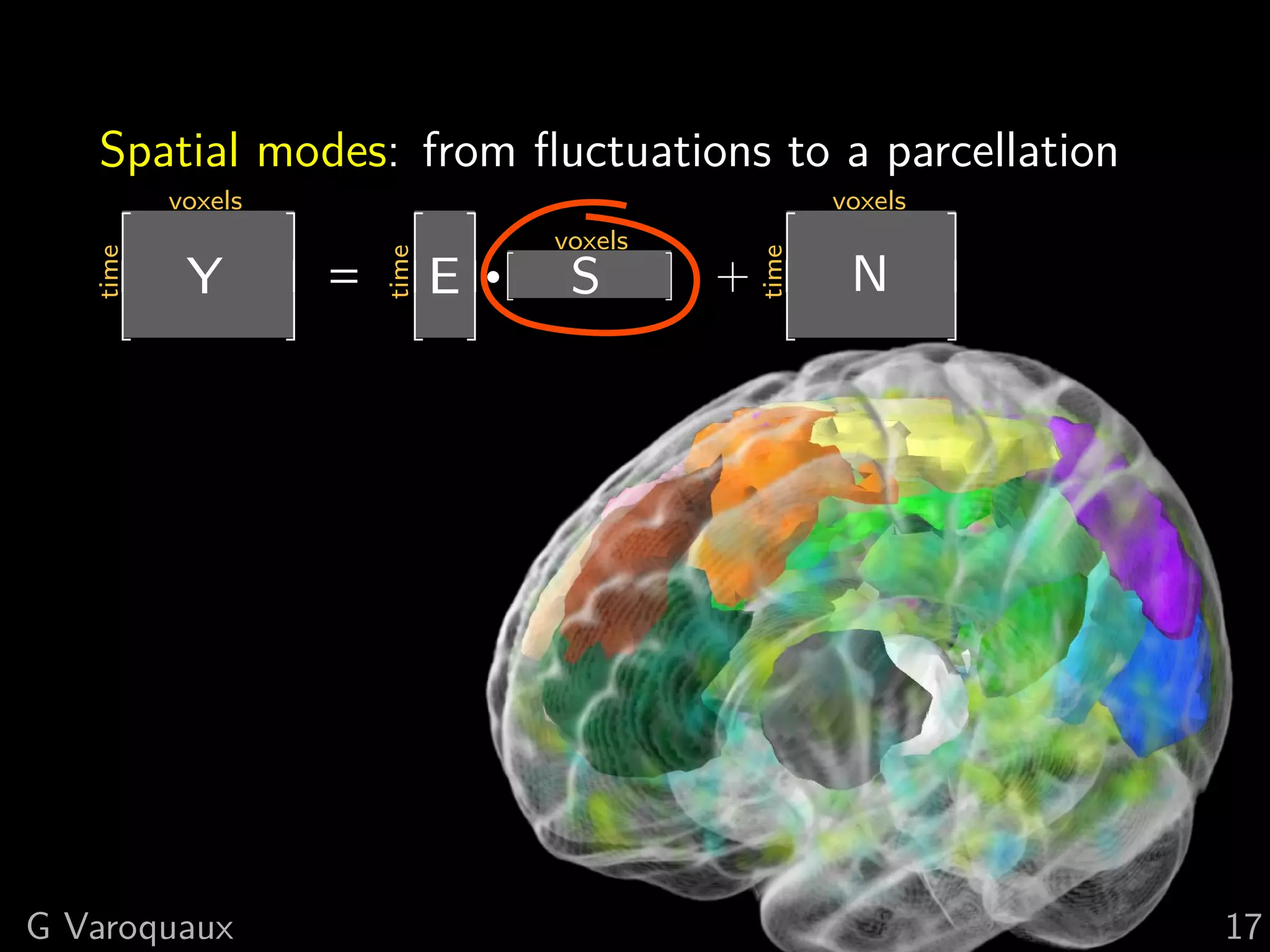
19. 1 The group-level ICA maps
ICA extracts a brain parcellation
However
No overall control of residuals
Does not select for what we interpret
G Varoquaux [Varoquaux NeuroImage 2010] 12

20. 1 Multi-subject dictionary learning
Subject Group
Time series maps maps
25 x
Subject level spatial patterns:
Ys = Us Vs T + Es , Es ∼ N (0, σI)
Group level spatial patterns:
Vs = V + Fs , Fs ∼ N (0, ζI)
Sparsity and spatial-smoothness prior:
1
V ∼ exp (−ξ Ω(V)), Ω(v) = v 1 + vT Lv
2
G Varoquaux [Varoquaux Inf Proc Med Imag 2011] 13

21. 1 Multi-subject dictionary learning
Estimation: maximum a posteriori
argmin Ys − Us Vs T 2
Fro + µ Vs − V 2
Fro + λ Ω(V)
Us ,Vs ,V sujets
Data fit Subject Penalization: sparse
variability and smooth maps
Alternate optimization on Us , Vs , V:
Update Us : standard dictionary learning procedure
[Mairal2010]
Update Vs : ridge regression on (Vs − V)T
Update V: proximal operator for λ Ω:
S
1 s
argmin v −v 2
2 + γ Ω(v) = prox ¯,
v V = mean Vs
¯
v s=1 2
γ/
S Ω s
G Varoquaux [Varoquaux Inf Proc Med Imag 2011] 14

22. 1 Multi-subject dictionary learning
Estimation: maximum a posteriori
argmin Ys − Us Vs T 2
Fro + µ Vs − V 2
Fro + λ Ω(V)
Us ,Vs ,V sujets
Data fit Subject Penalization: sparse
variability and smooth maps
Parameter selection
µ: comparing variance (PCA spectrum) at subject
and group level
λ: cross-validation
G Varoquaux [Varoquaux Inf Proc Med Imag 2011] 14

23. 1 Multi-subject dictionary learning
Individual maps + Atlas of functional regions
G Varoquaux [Varoquaux Inf Proc Med Imag 2011] 15

24. 1 Multi-subject dictionary learning
Multi-subject dictionary learning ICA
G Varoquaux [Varoquaux Inf Proc Med Imag 2011] 16

25. 1 Multi-subject dictionary learning
Multi-subject dictionary learning ICA
G Varoquaux [Varoquaux Inf Proc Med Imag 2011] 16

26. 1 Multi-subject dictionary learning
Default mode Base ganglia
G Varoquaux [Varoquaux Inf Proc Med Imag 2011] 16

27. Spatial modes: from fluctuations to a parcellation
voxels voxels
voxels
Y E · S + N
time
time
time
=
G Varoquaux 17

28. Associated time series:
voxels voxels
voxels
Y E · S + N
time
time
time
=
G Varoquaux 17

29. 2 Graphical models of brain
connectivity
Modeling the correlations between
regions
G Varoquaux 18

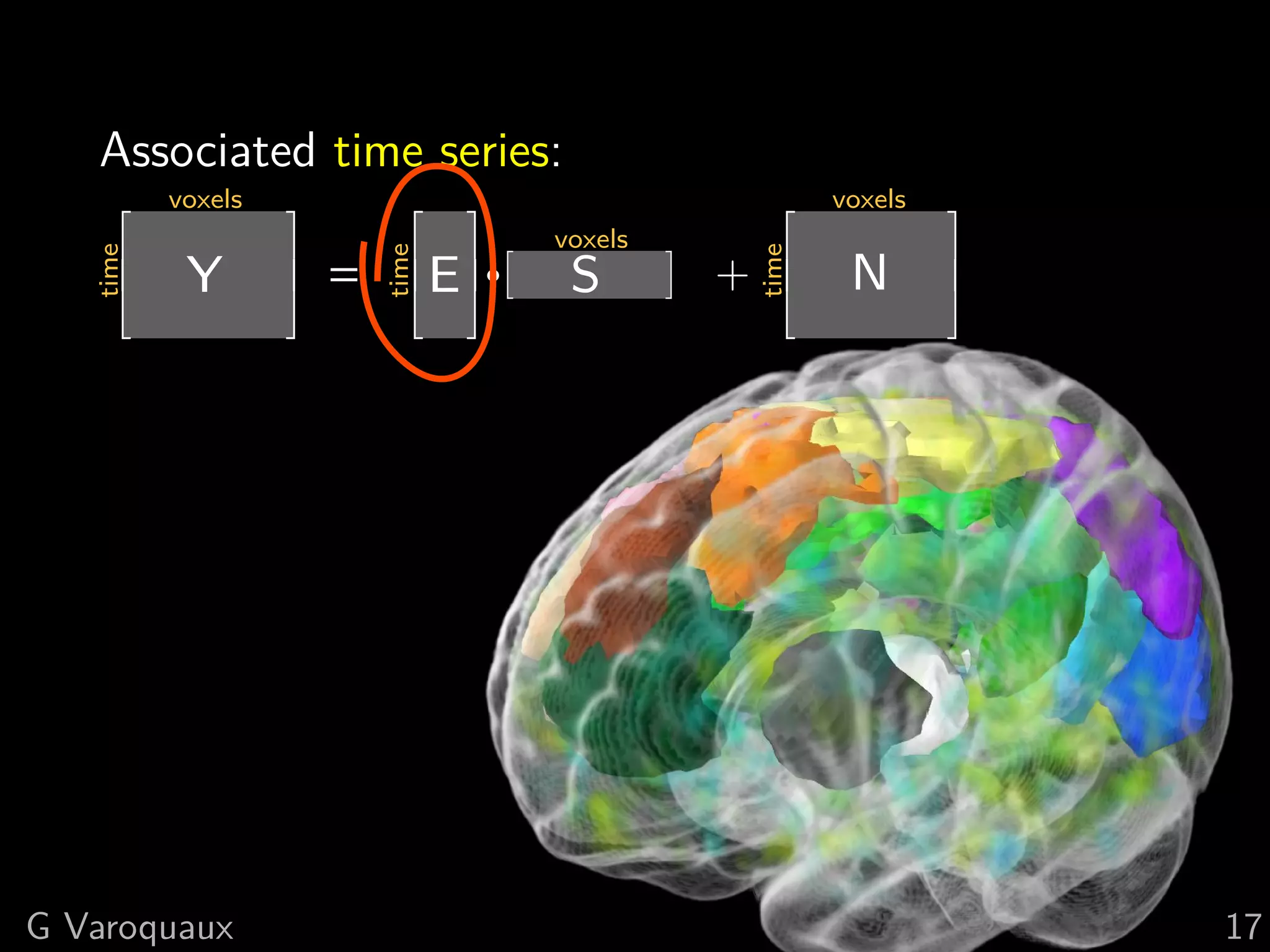
30. 2 Graphical model for correlation
Specify the probability of observing fMRI data
Multivariate normal P(X) ∝ |Σ−1 |e − 2 X Σ X
1 T −1
Parametrized by inverse covariance matrix K = Σ−1
Observations: Direct connections:
Covariance matrix Inverse covariance
1 1
2 2
0 0
3 3
4 4
[Smith 2011, Varoquaux NIPS 2010]
G Varoquaux 19

31. 2 Penalized sparse inverse covariance estimation
Maximum a posteriori: fit models with a prior
K = argmax L(Σ|K) + f (K)
ˆ
K 0
Standard sparse inverse-covariance estimation:
Prior: many pairs of regions are not connected
Lasso-like problem:
1 penalization f (K) = |Ki,j |
i=j
G Varoquaux 20

32. 2 Penalized sparse inverse covariance estimation
Maximum a posteriori: fit models with a prior
K = argmax L(Σ|K) + f (K)
ˆ
K 0
Our contribution: Population prior:
same independence structure across subjects
⇒ Estimate together all {Ks } from {Σs }
ˆ
A. Gramfort
Group-lasso (mixed norms):
21 penalization f {Ks } = λ (Ks )2
i,j
i=j s
Convex optimization problem
G Varoquaux [Varoquaux NIPS 2010] 20

33. 2 Population-sparse graph perform better
ˆ
Σ−1
Sparse
inverse
Population
prior
Likelihood of new data (nested cross-validation)
Subject data, Σ−1 -57.1
Subject data, sparse inverse 43.0
Group average data, Σ−1 40.6
Group average data, sparse inverse 41.8
Population prior 45.6
G Varoquaux [Varoquaux NIPS 2010] 21

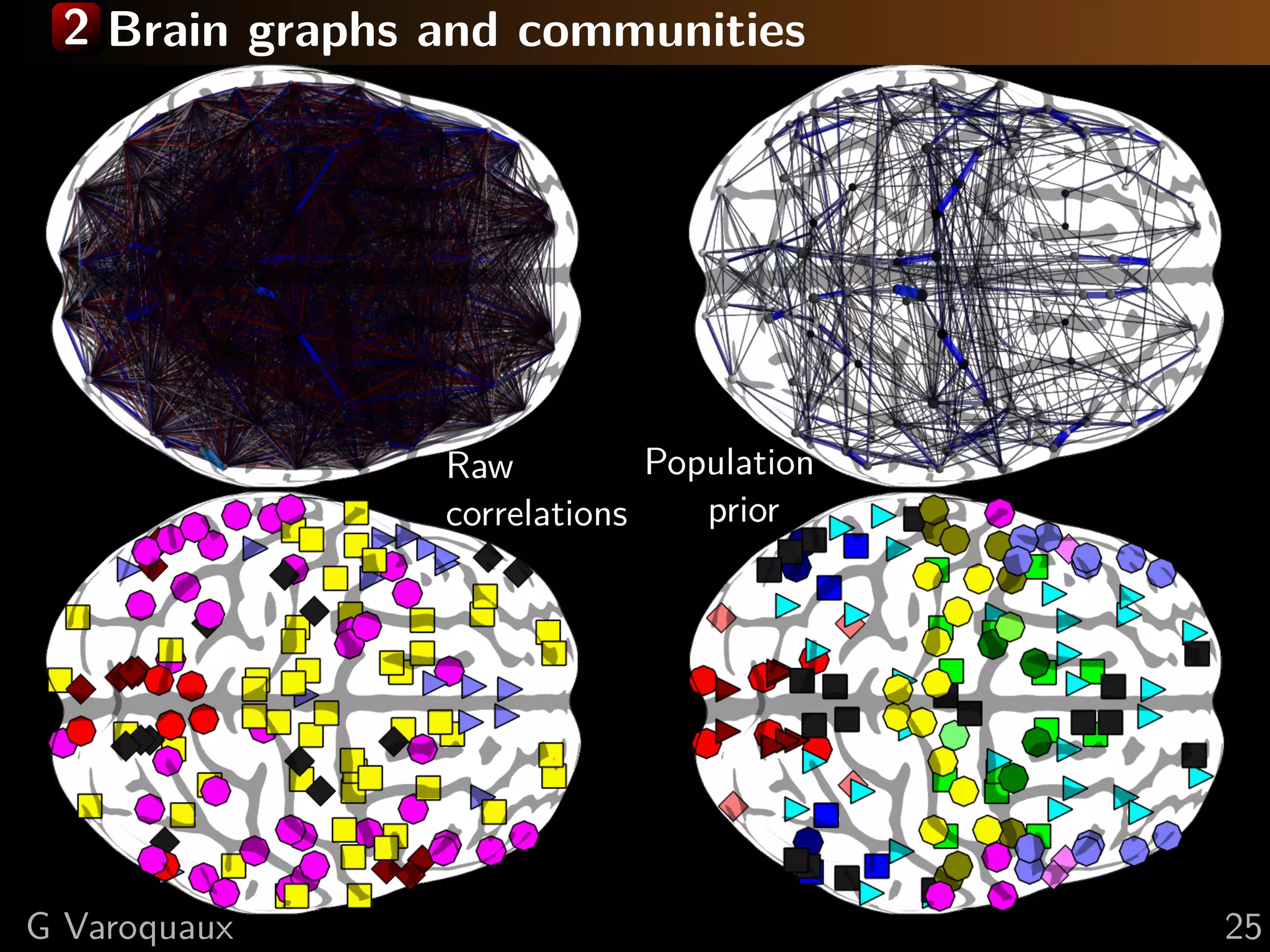
34. 2 Brain graphs
Raw Population
correlations prior
G Varoquaux [Varoquaux NIPS 2010] 22

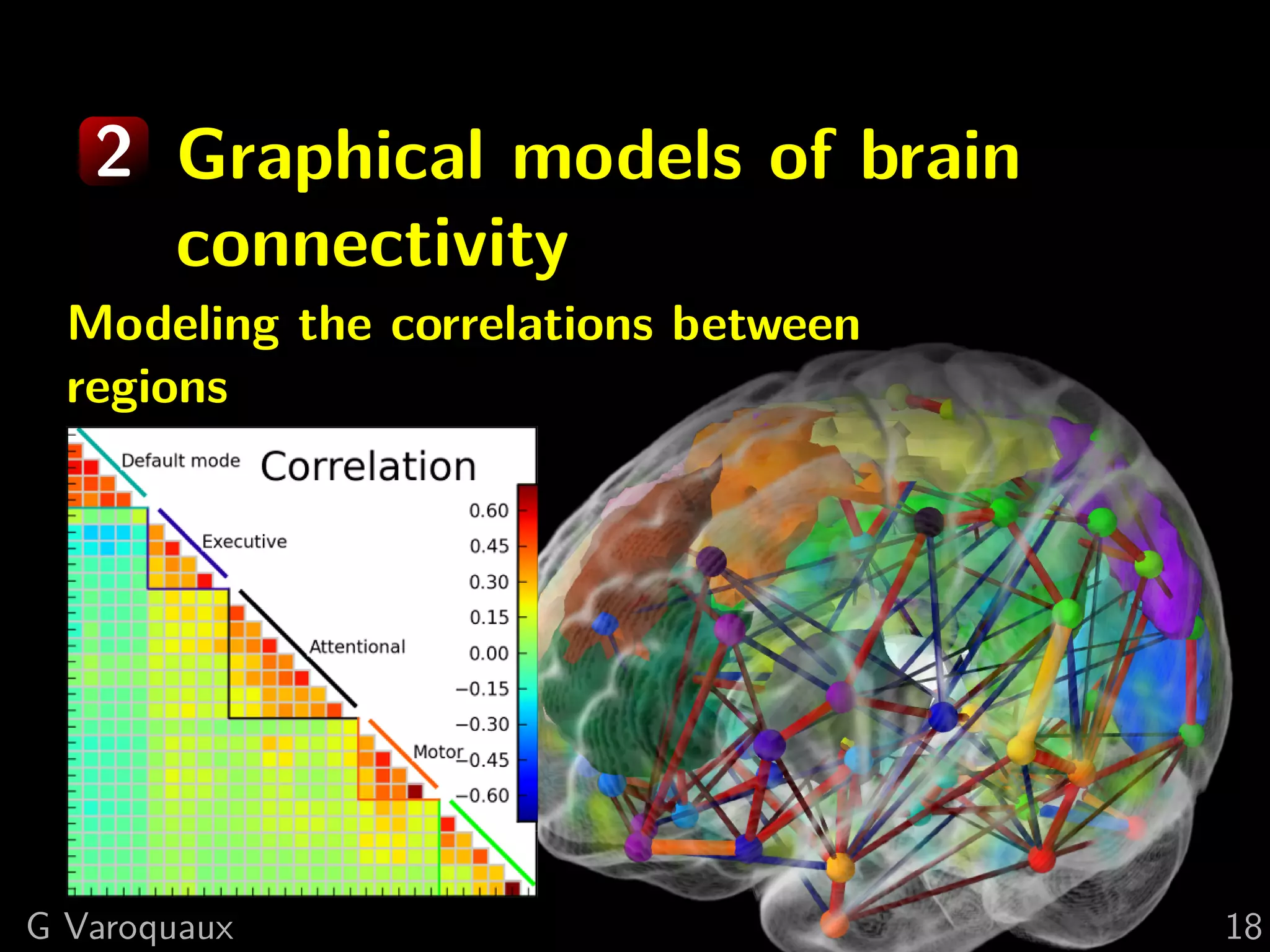
35. 2 Graphs of brain function?
Cognitive function arises from the interplay of
specialized brain regions:
The functional segregation of local areas [...]
contrasts sharply with their global integration during
perception and behavior [Tononi 1994]
A proposed measure of functional segregation
Graph modularity =
divide in communities to
maximize intra-class connections
versus extra-class
G Varoquaux 23

36. 2 Graph cuts to isolate functional communities
Find communities to maximize modularity:
  2 
k A(Vc , Vc )  A(V , Vc ) 
Q=  − 
c=1 A(V , V ) A(V , V )
A(Va , Vb ) is the sum of edges going from Va to Vb
Rewrite as an eigenvalue problem [White 2005]
1
1
0
0
A · 1 1 0 0
⇒ Spectral clustering = spectral embedding + k-means
Similar to normalized graph cuts
G Varoquaux 24

37. 2 Brain graphs and communities
Raw Population
correlations prior
G Varoquaux 25

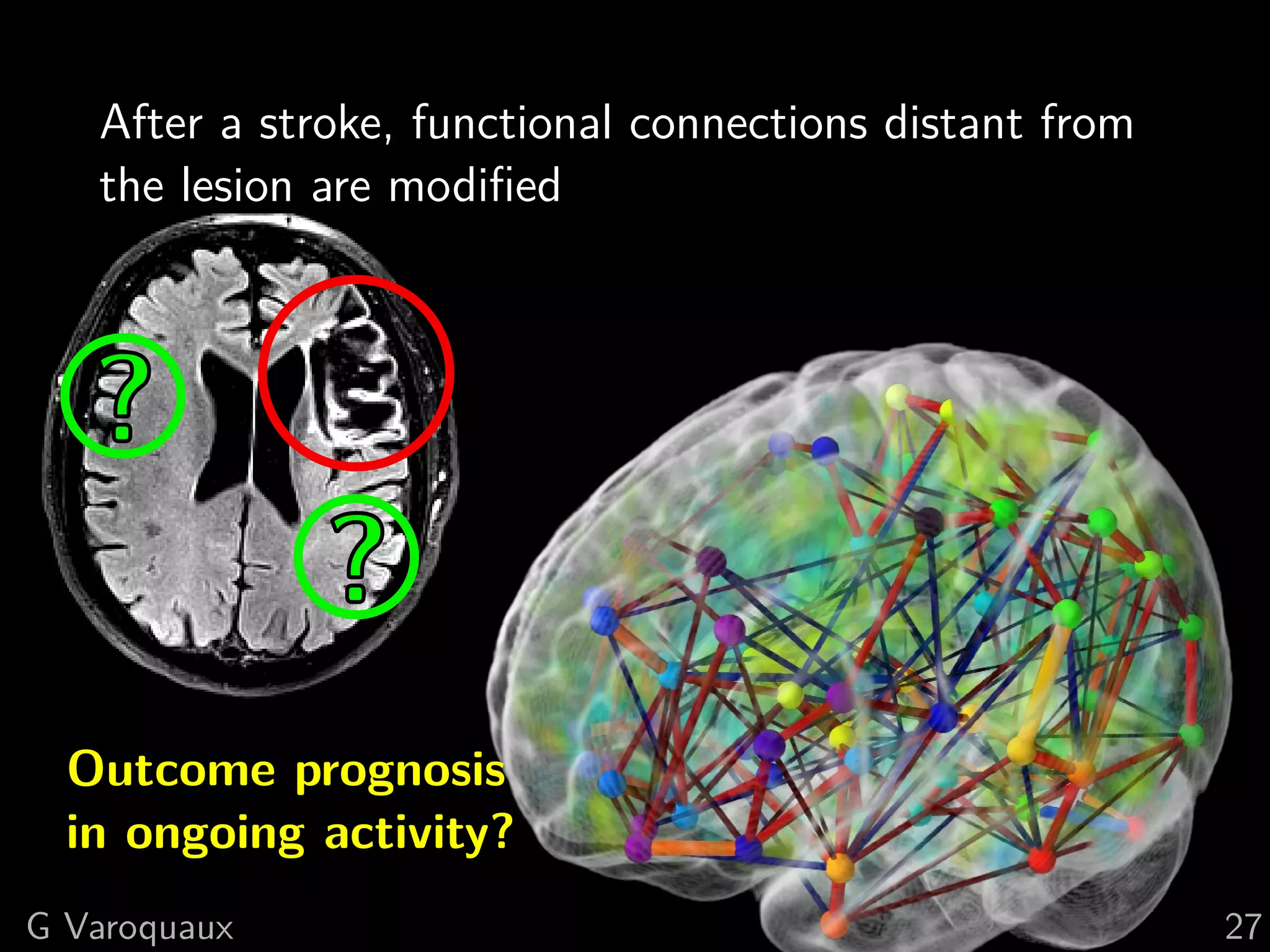
38. 2 Brain integration between communities
Proposed measure for functional integration:
mutual information (Tononi)
1
Integration: Ic1 = log det(Kc1 )
2
Mutual information: Mc1 ,c2 = Ic1 ∪c2 − Ic1 − Is2
G Varoquaux [Varoquaux NIPS 2010] 26

39. 2 Brain integration between communities
Proposed measure for functional integration:
mutual information (Tononi)
With population prior: Occipital pole
Default mode network visual areas Medial visual areas
Fronto-parietal Lateral visual
networks areas
Fronto-lateral Posterior inferior
network temporal 1
Pars Posterior inferior
opercularis temporal 2
Raw Dorsal motor Right Thalamus
correlations: Cingulo-insular
Ventral motor network
Auditory Left Putamen
Basal ganglia
G Varoquaux [Varoquaux NIPS 2010] 26

40. Map functional connections of individuals
in a population
G Varoquaux 27

41. After a stroke, functional connections distant from
the lesion are modified
?
?
Outcome prognosis
in ongoing activity?
G Varoquaux 27

42. 3 Detecting differences in
connectivity
G Varoquaux 28

43. 3 Failure of univariate approach on correlations
Subject variability spread across correlation matrices
0 0 0 0
5 5 5 5
10 10 10 10
15 15 15 15
20 20 20 20
25 Control 25 Control 25 Control Large lesion
25
0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25
Cannot apply univariate statistics
Σ1 Σ2 dΣ = Σ2 − Σ1
dΣ = Σ2 − Σ1 is not definite positive
⇒ Describes impossible observations (negative variance)
G Varoquaux 29

44. 3 Failure of univariate approach on correlations
Subject variability spread across correlation matrices
0 0 0 0
5 5 5 5
10 10 10 10
15 15 15 15
20 20 20 20
25 Control 25 Control 25 Control Large lesion
25
0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25
Cannot apply univariate statistics
in contradiction with Gaussian models:
parameters not independent
Σ does not live in a vector space
G Varoquaux 29

45. 3 Simulation on a toy problem
Simulate two processes with different inverse covariance
K1 : K1 − K2 : Σ1 : Σ1 − Σ2 :
Add jitter in observed covariance... sample
MSE(K1 − K2 ): MSE(Σ1 − Σ2 ):
Non-local effects and non homogeneous noise
G Varoquaux 30

46. 3 Theoretical settings: comparison of estimates
Observations in 2 populations: X1 and X2
ˆ ˆ
Goal: comparing estimates: θ(X1 ) and θ(X1 )
Asymptotic normality: θ(X1 ) ∼ N θ1 , I(θ1 )−1
ˆ
I(θ²)
-1
θ²
I(θ¹)
-1
θ¹
G Varoquaux 31

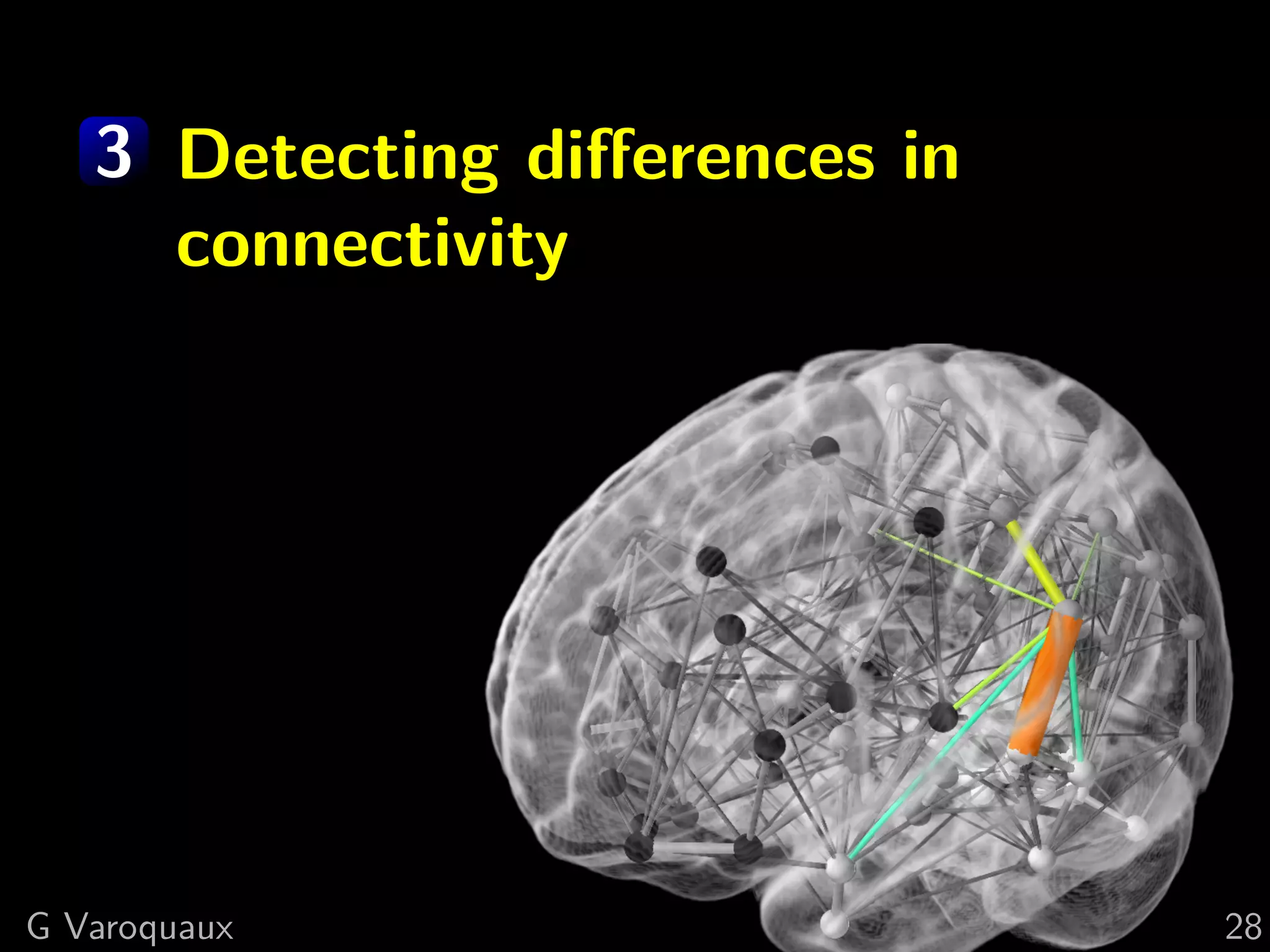
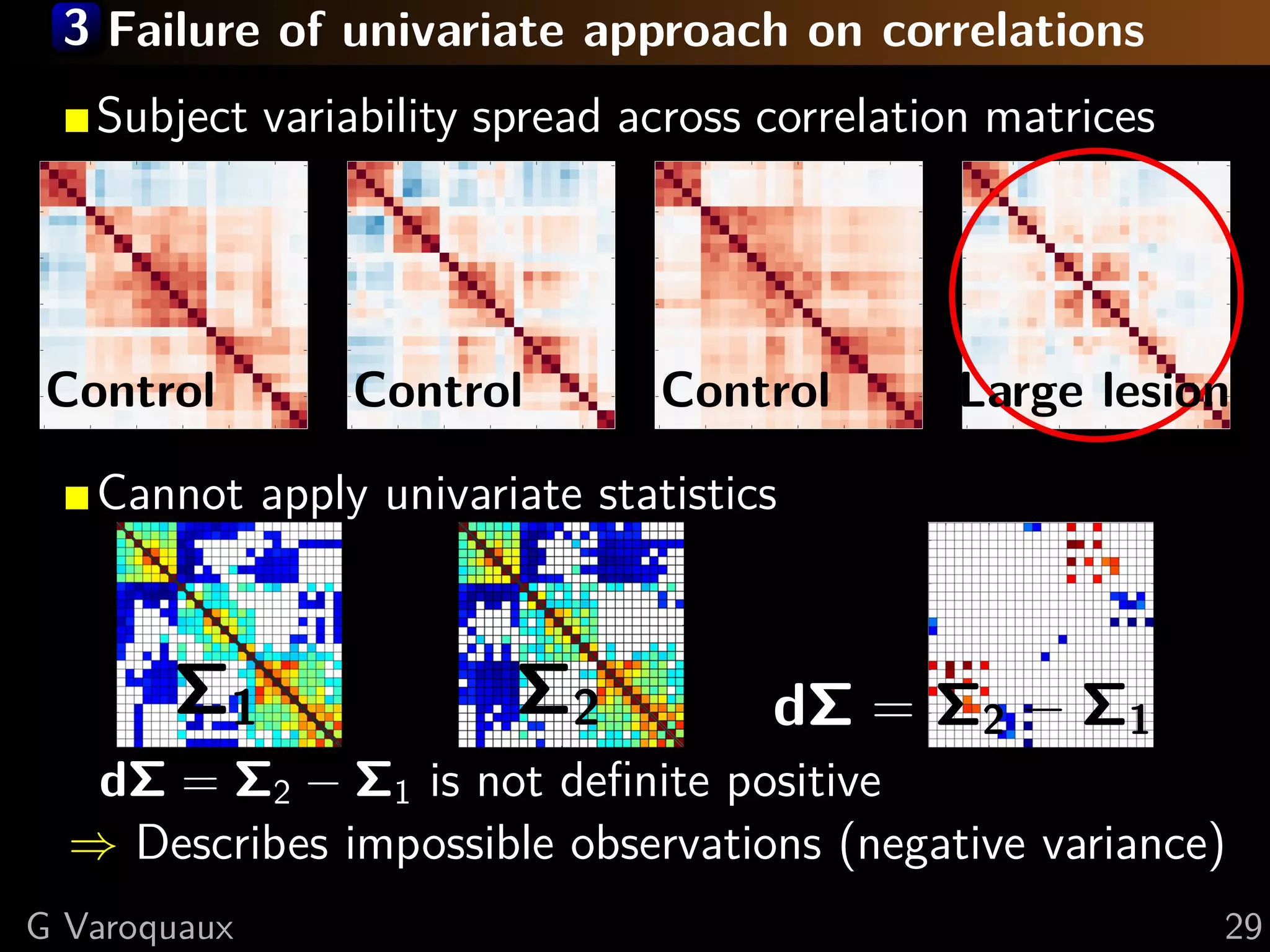
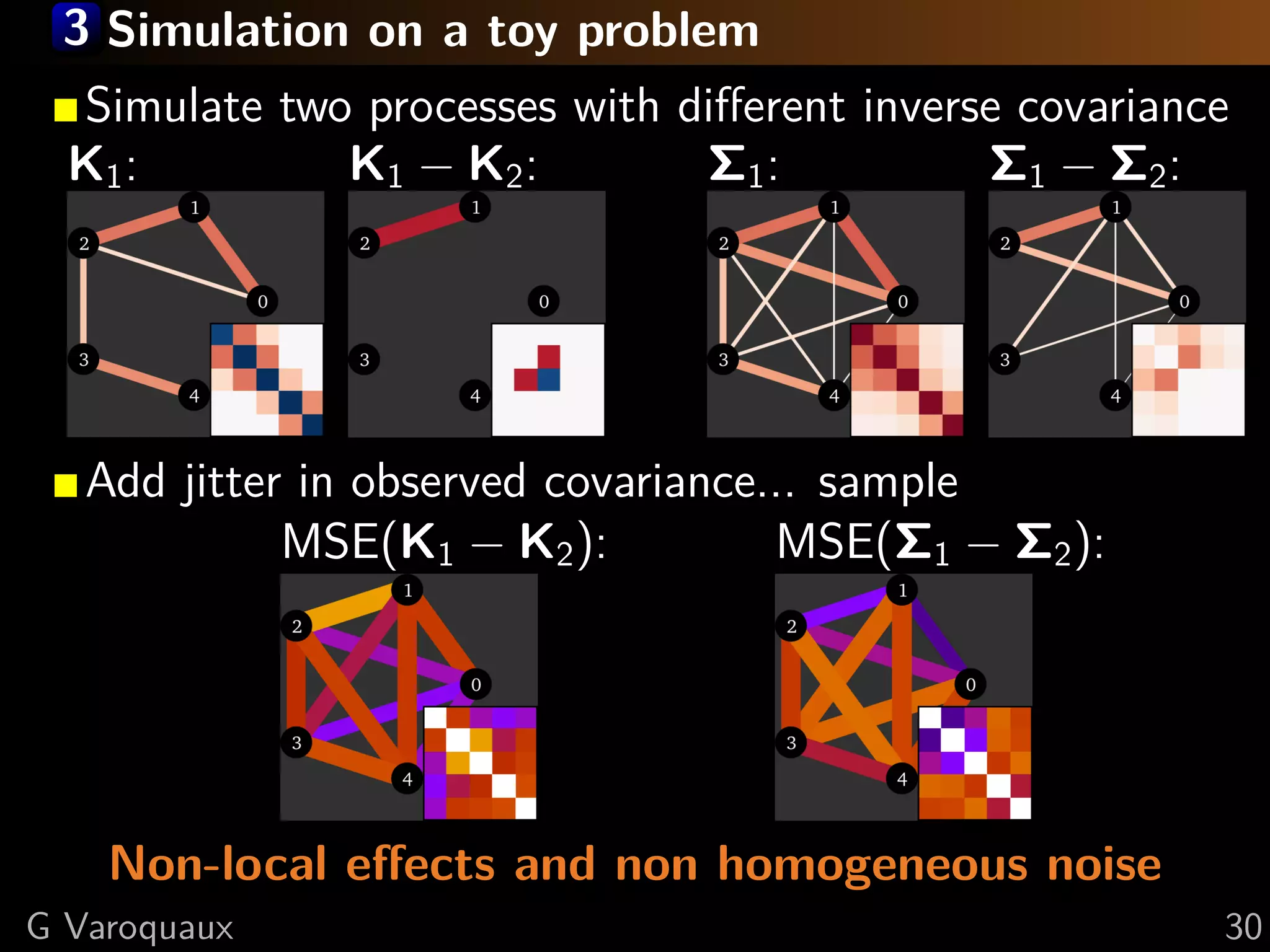
47. 3 Theoretical settings: comparison of estimates
[Rao 1945] Fisher information I defines a metric on
the manifold of models.
We use it to choose a global parametrization for
comparisons
if old
an
M
G Varoquaux 31

48. 3 Covariance manifold – Symn
+
Metric tensor (Fisher information) [Lenglet 2006]
dΣ1 , dΣ2 Σ = 1 trace(Σ−1 dΣ1 Σ−1 dΣ2 )
2
+
Nice properties of the Symn manifold (Lie group):
metric can be fully integrated, gives rise to global
mapping to a vector space (Logarithmic map).
Σ1 , Σ2 = log Σ1 − 2 Σ2 Σ1 − 2
2 1 1 2
Σ1
,
Locally: Σ1 , Σ2 ∝ trace(Σ1 − 2 Σ2 Σ1 − 2 ) − p
1 1
Σ1
= dΣ Fro
dΣ = Σ1 Σ2 Σ1
−1/2 −1/2
where
G Varoquaux 32

49. 3 Reparametrization for uniform error geometry
Logarithmic mapping:
−−
−→
Σ1 ∈ Symn Σ2 ∈ Symn → Σ1 Σ2 ∈ R 2 p (p−1)
1
+ +
Controls
Patient
Controls
Patient
G Varoquaux 33

50. 3 Reparametrization for uniform error geometry
Logarithmic mapping:
−−
−→
Σ1 ∈ Symn Σ2 ∈ Symn → Σ1 Σ2 ∈ R 2 p (p−1)
1
+ +
−−
−→
d(Σ1 , Σ2 ) = Σ1 Σ2 2
old
a nif
M
Tangen
dΣ t
Controls
Patient
G Varoquaux 33

51. 3 Statistics...
Do intrinsic statistics on the parameterization:
Mean (Frechet mean)
PDF
Parameter-level hypothesis testing
G Varoquaux 34

52. 3 Random effects on the covariance manifold
Population-level covariance distribution
Generalized isotropic normal distribution:
 
1
p(Σ) = k(σ) exp− 2 Σ Σ 2 Σ
 (1)
2σ
Population mean:
Σ = argmin ΣΣi 2
Σ (2)
Σ i
Efficient gradient descent algorithm
Principled computation of:
group mean Σ and spread σ
likelihood of new data
G Varoquaux 35

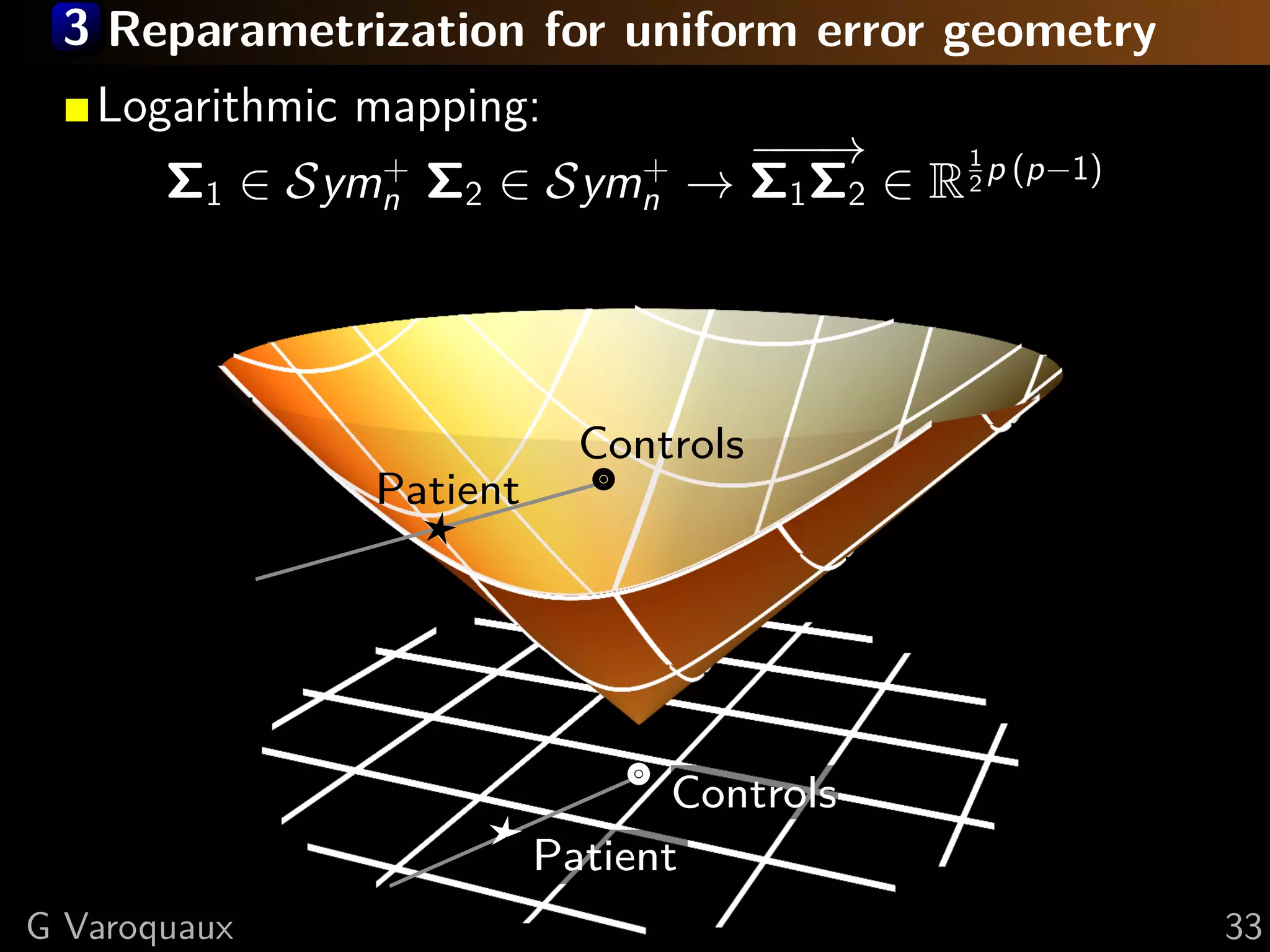
53. 3 Random effects on the covariance manifold
Population-level covariance distribution
Generalized isotropic normal distribution:
 
1
p(Σ) = k(σ) exp− 2 Σ Σ 2 Σ
 (1)
2σ
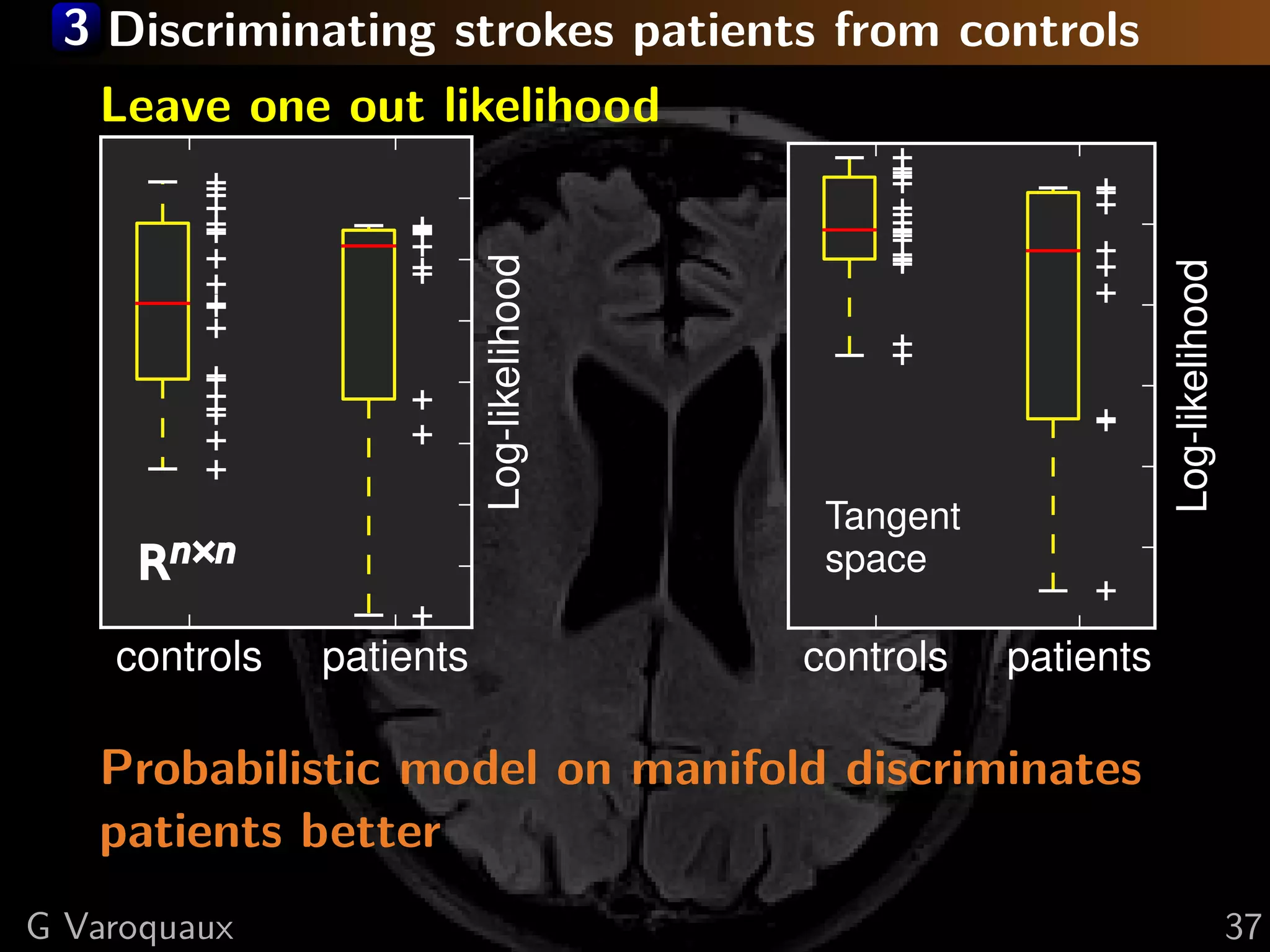
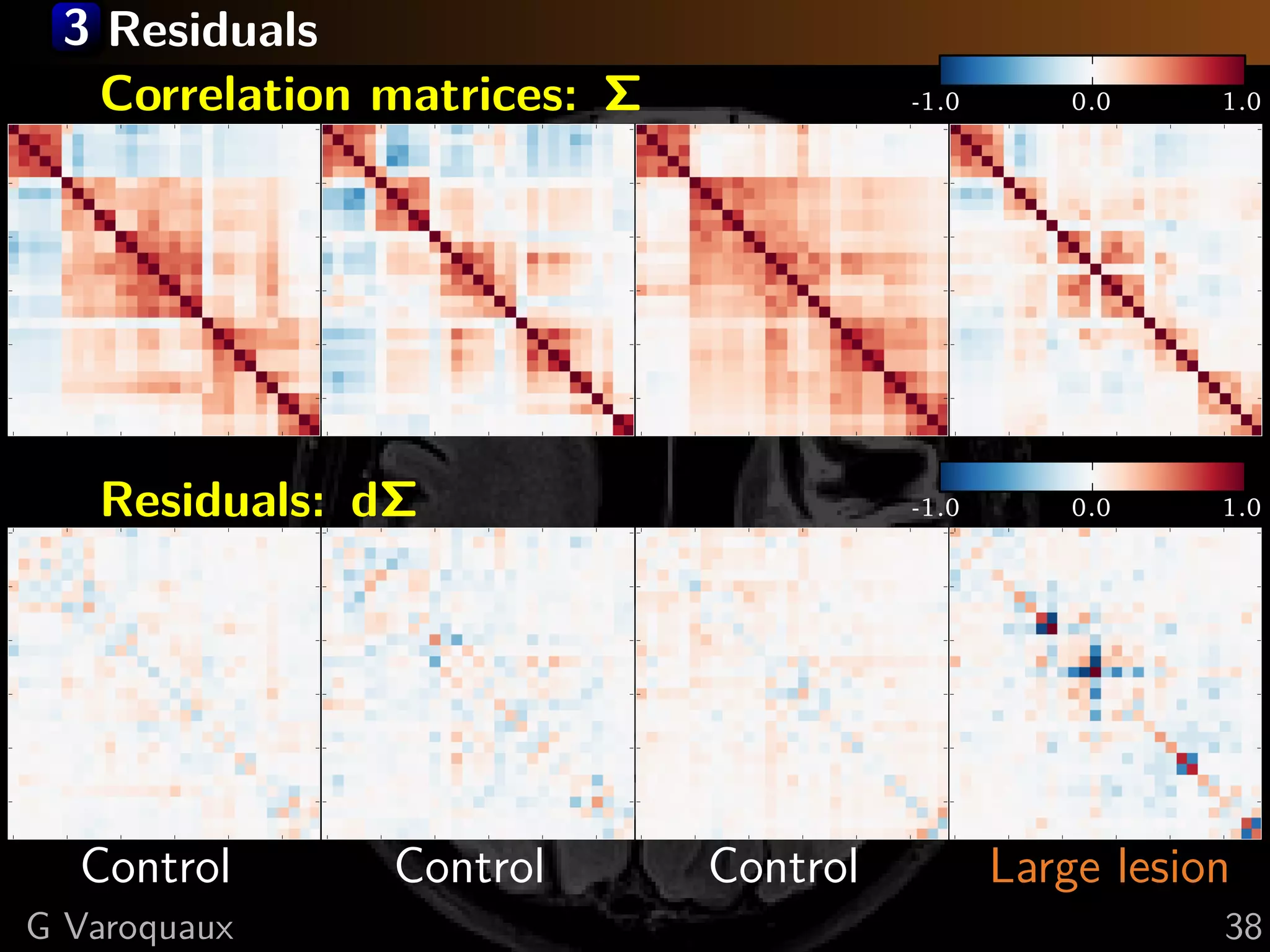
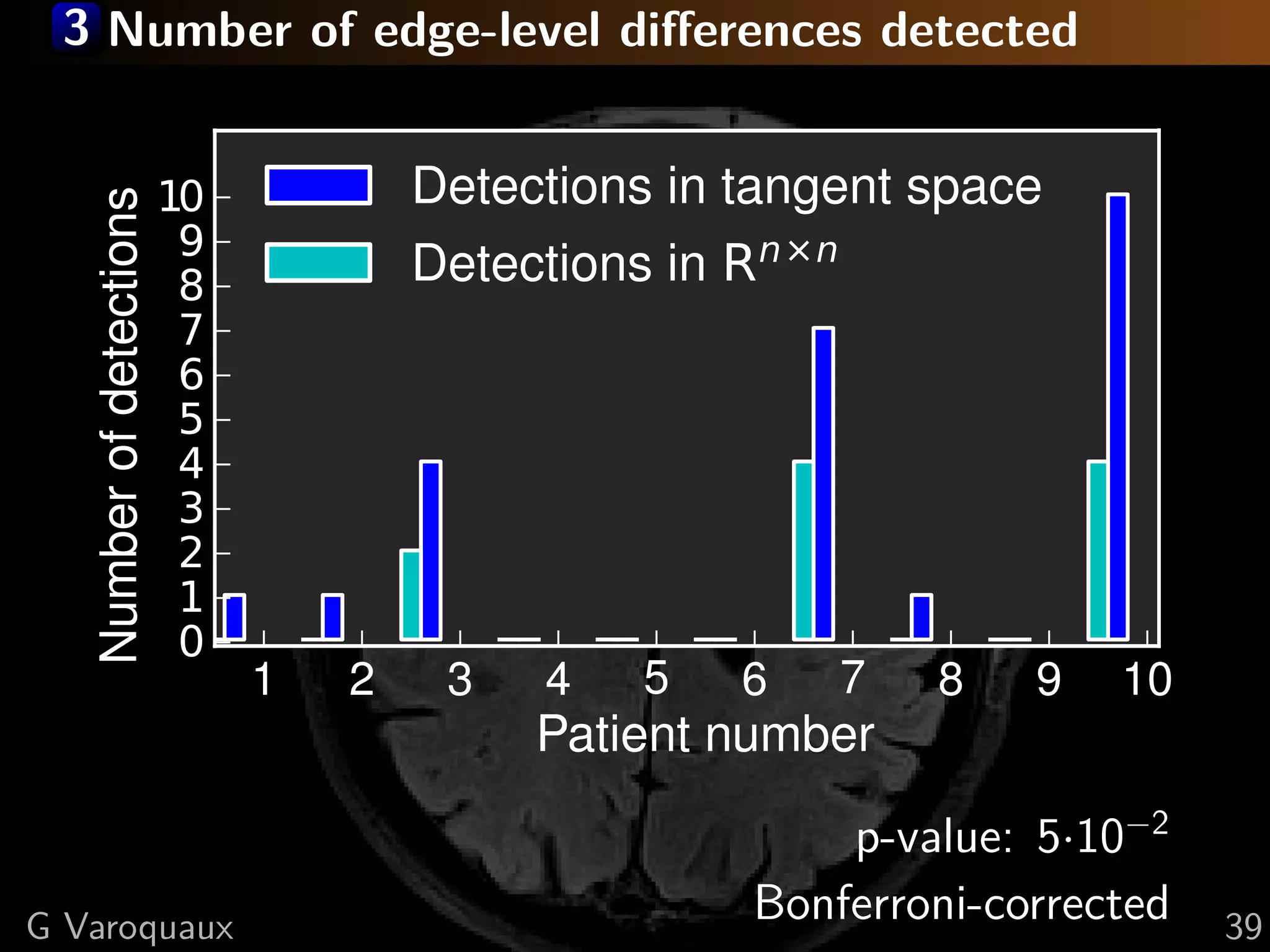
Edge-level statistics
Under null hypothesis: subject ∈ group model (1)
−→
dΣ ∼ N (0, σI) : Independant coefficients
⇒ Univariate statistics on dΣi,j
[Varoquaux MICCAI 2010]
G Varoquaux 35

54. 3 Discriminating strokes patients from controls
20 controls – 10 stroke patients, all different
A. Kleinschmidt F. Baronnet
G Varoquaux 36

55. 3 Discriminating strokes patients from controls
Leave one out likelihood
Log-likelihood
Log-likelihood
Tangent
n×n space
R
controls patients controls patients
Probabilistic model on manifold discriminates
patients better
G Varoquaux 37

56. 3 Residuals
0
Correlation matrices: Σ
0 0
-1.0
0
0.0 1.0
5 5 5 5
0 10 10 10
5 15 15 15
0 20 20 20
5 25 25 25
0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25
0
Residuals: dΣ
0 0
-1.0
0
0.0 1.0
5 5 5 5
0 10 10 10
5 15 15 15
0 20 20 20
5 25 25 25
0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25
Control Control Control Large lesion
G Varoquaux 38

57. 3 Number of edge-level differences detected
10 Detections in tangent space
Number of detections
9
8 Detections in Rn×n
7
6
5
4
3
2
1
0
1 2 3 4 5 6 7 8 9 10
Patient number
p-value: 5·10−2
G Varoquaux
Bonferroni-corrected 39

58. 3 Post-stroke covariance modifications
p-value: 5·10−2
Bonferroni-corrected
G Varoquaux 40

59. 3 Post-stroke covariance modifications
p-value: 5·10−2
Bonferroni-corrected
G Varoquaux 40

60. Thanks
B. Thirion, J.B. Poline, A. Kleinschmidt
Resting state analysis S. Sadaghiani
Dictionary learning F. Bach, R. Jenatton
Sparse inverse covariance A. Gramfort
Strokes F. Baronnet
Matrix-variate MFX P. Fillard
Software: in Python
scikit-learn: machine learning
F. Pedegrosa, O. Grisel, M. Blondel . . .
Mayavi: 3D plotting
P. Ramachandran
G Varoquaux 41

61. Multi-subject functional connectivity mapping
A consistent full-brain model
Probabilistic generative model
With explicit inter-subject variability
Suitable for inference
Y = E · S + N
25
Population-level data analysis
Functional atlases
Large-scale graphical models
Inter-subject discrimination
G Varoquaux 42

62. Bibliography
[Varoquaux NeuroImage 2010] G. Varoquaux, S. Sadaghiani, P. Pinel, A.
Kleinschmidt, J.B. Poline, B. Thirion A group model for stable multi-subject ICA
on fMRI datasets, NeuroImage 51 p. 288 (2010)
http://hal.inria.fr/hal-00489507/en
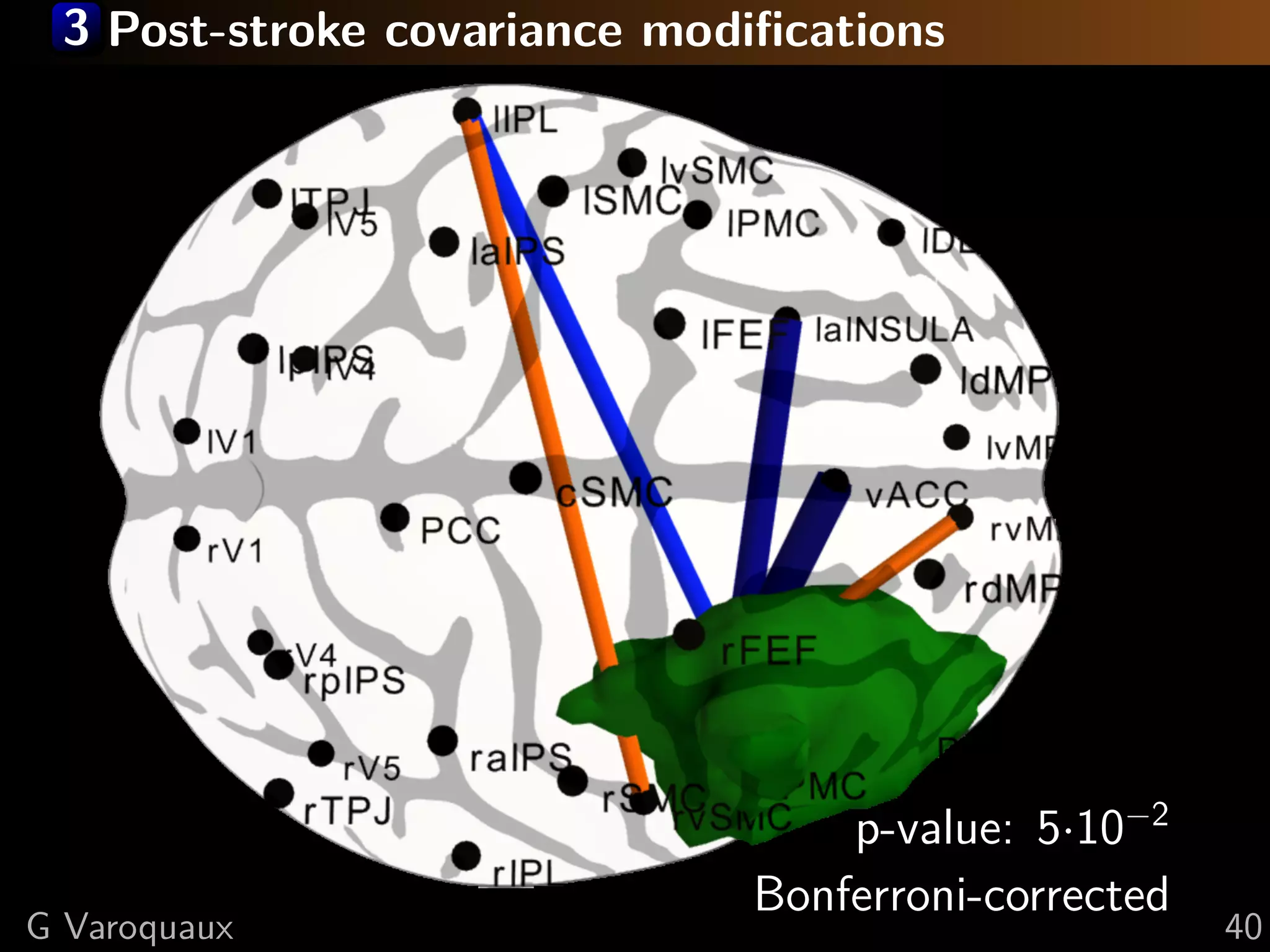
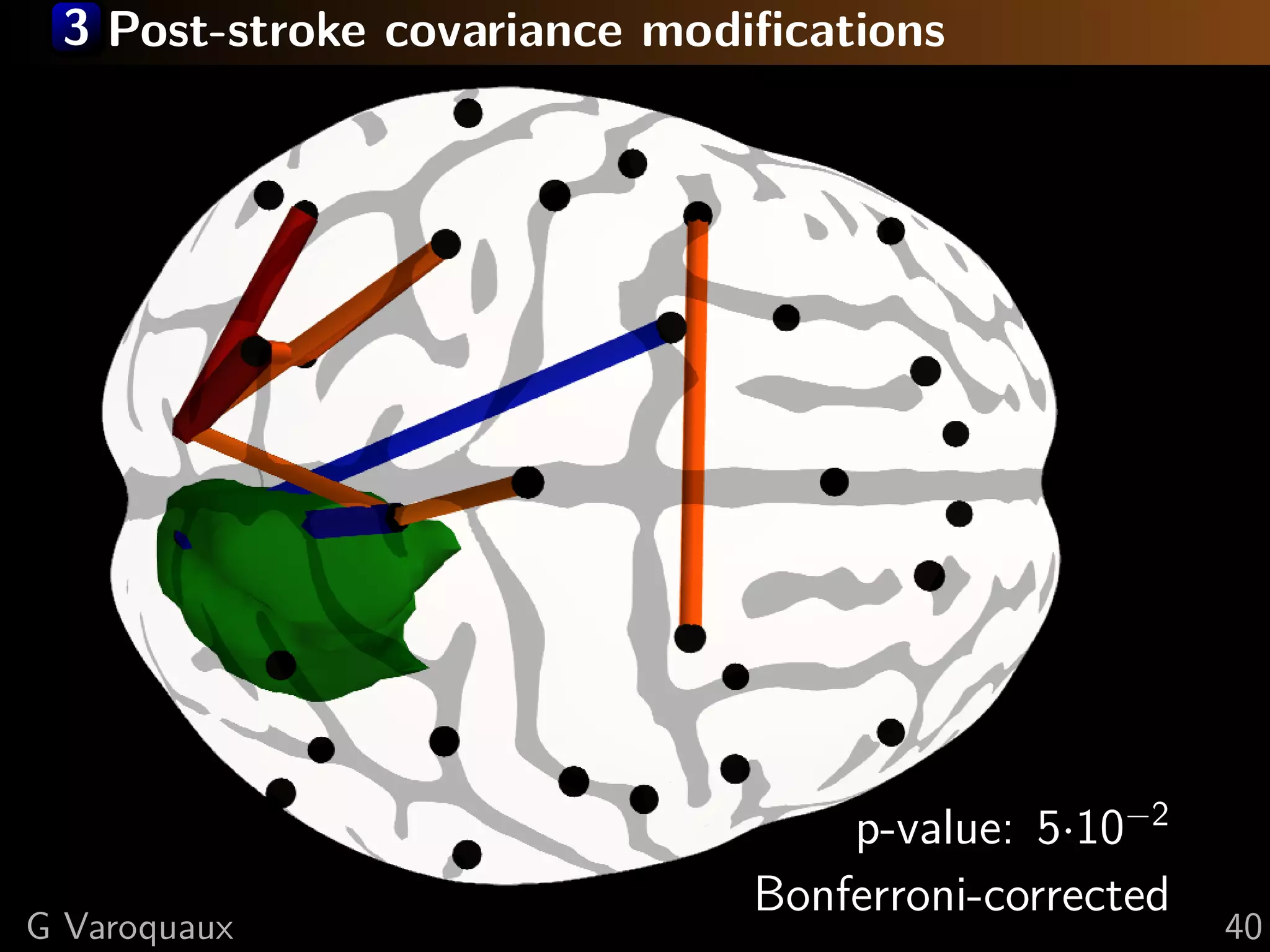
[Varoquaux MICCAI 2010] G. Varoquaux, F. Baronnet, A. Kleinschmidt, P.
Fillard and B. Thirion, Detection of brain functional-connectivity difference in
post-stroke patients using group-level covariance modeling, MICCAI (2010)
http://hal.inria.fr/inria-00512417/en
[Varoquaux NIPS 2010] G. Varoquaux, A. Gramfort, J.B. Poline and B. Thirion,
Brain covariance selection: better individual functional connectivity models using
population prior, NIPS (2010)
http://hal.inria.fr/inria-00512451/en
[Varoquaux IPMI 2011] G. Varoquaux, A. Gramfort, F. Pedregosa, V. Michel,
and B. Thirion, Multi-subject dictionary learning to segment an atlas of brain
spontaneous activity, Information Processing in Medical Imaging p. 562 (2011)
http://hal.inria.fr/inria-00588898/en
[Ramachandran 2011] P. Ramachandran, G. Varoquaux Mayavi: 3d visualization
of scientific data, Computing in Science & Engineering 13 p. 40 (2011)
http://hal.inria.fr/inria-00528985/en
G Varoquaux 43