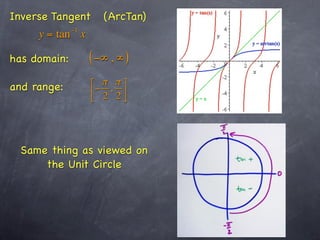
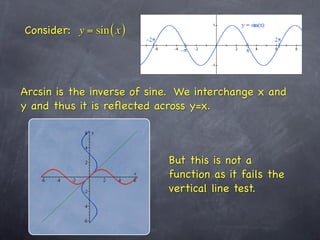
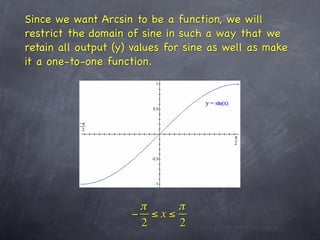
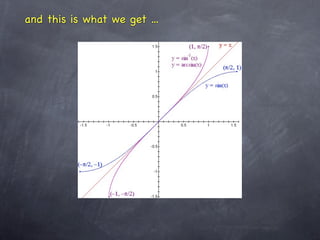
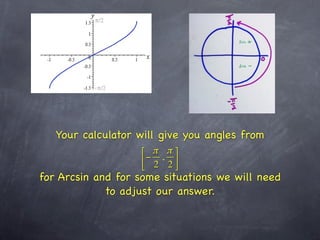
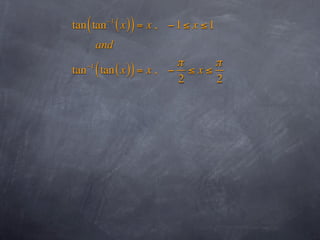This document discusses inverse trigonometric functions including arcsine, arccosine, and arctangent. It explains that arcsine is the inverse of sine, with domain [-1,1] and range [-π/2, π/2]. Arccosine has domain [-1,1] and range [0,π]. Arctangent has domain (-∞, ∞) and range [-π/2, π/2]. The document also notes that applying the inverse function twice returns the original value, and the outer function's domain takes precedence when functions are composed. It recommends graphing the inverse trig functions to better understand their properties.

1. 7.4 Inverse Trig Functions
2 Corinthians 12:9-10
But he said to me, "My grace is sufficient for you, for
my power is made perfect in weakness." Therefore I
will boast all the more gladly about my weaknesses, so
that Christ's power may rest on me. That is why, for
Christ's sake, I delight in weaknesses, in insults, in
hardships, in persecutions, in difficulties. For when I am
weak, then I am strong.

2. Consider: y = sin ( x )

3. Consider: y = sin ( x )
Arcsin is the inverse of sine. We interchange x and
y and thus it is reflected across y=x.

4. Consider: y = sin ( x )
Arcsin is the inverse of sine. We interchange x and
y and thus it is reflected across y=x.

5. Consider: y = sin ( x )
Arcsin is the inverse of sine. We interchange x and
y and thus it is reflected across y=x.
But this is not a
function as it fails the
vertical line test.

6. Since we want Arcsin to be a function, we will
restrict the domain of sine in such a way that we
retain all output (y) values for sine as well as make
it a one-to-one function.
π π
− ≤x≤
2 2

7. and this is what we get ...

8. Inverse Sine (Arcsin)
−1
y = sin x
has domain: [ −1 , 1]
⎡ π π ⎤
and range: ⎢ − 2 , 2 ⎥
⎣ ⎦

9. Inverse Sine (Arcsin)
−1
y = sin x
has domain: [ −1 , 1]
⎡ π π ⎤
and range: ⎢ − 2 , 2 ⎥
⎣ ⎦
Same thing as viewed on
the Unit Circle

10. Your calculator will give you angles from
⎡ π π ⎤
− , ⎥
⎢ 2 2 ⎦
⎣
for Arcsin and for some situations we will need
to adjust our answer.

11. Inverse Cosine (ArcCos)
−1
y = cos x
has domain: [ −1 , 1]
and range: [ 0, π ]
Same thing as viewed on
the Unit Circle

12. Inverse Tangent (ArcTan)
−1
y = tan x
has domain: ( −∞ , ∞ )
and range: ⎡ π π ⎤
⎢ − 2 , 2 ⎥
⎣ ⎦
Same thing as viewed on
the Unit Circle

13. Recall ... ( )
f f ( x) = x
−1
and f ( f ( x )) = x
−1
and that the outer function’s domain takes precedence.
Therefore:

14. Recall ... (
f f ( x) = x
−1
)
and f ( f ( x )) = x
−1
and that the outer function’s domain takes precedence.
Therefore:
sin ( sin −1
( x )) = x , −1 ≤ x ≤1
and
π π
sin ( sin ( x )) = x , − ≤ x ≤
−1
2 2

15. Recall ... (
f f ( x) = x
−1
)
and f ( f ( x )) = x−1
and that the outer function’s domain takes precedence.
Therefore:
sin ( sin −1
( x )) = x , −1 ≤ x ≤1
and
π π
sin ( sin ( x )) = x , − ≤ x ≤
−1
2 2
cos ( cos −1
( x )) = x , −1 ≤ x ≤1
and
cos −1
( cos ( x )) = x , 0≤ x ≤π

16. tan ( tan −1
( x )) = x , −1 ≤ x ≤1
and
π π
tan ( tan ( x )) = x , − ≤ x ≤
−1
2 2

17. tan ( tan −1
( x )) = x , −1 ≤ x ≤1
and
π π
tan ( tan ( x )) = x , − ≤ x ≤
−1
2 2
Please know that you calculator doesn’t graph these very
well. If time allows, graph y = sin x, y = cos x, y = tan x
−1 −1 −1
and discuss the limitations of our calculator.
Be sure you know what the graph really looks like!

18. No HW
Our most profitable lessons are learned from failure,
not success.
Frank Davidson