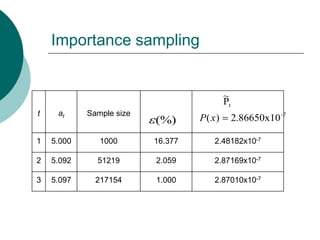
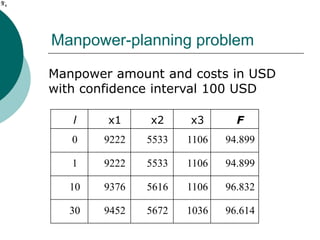
The document discusses nonlinear stochastic programming using the Monte Carlo method, covering aspects like stochastic unconstrained optimization, Monte Carlo estimators, and gradient-based algorithms. It presents a methodology for optimizing sample sizes and statistical testing of optimality in optimization problems, alongside specific applications such as manpower planning. The conclusions highlight the effectiveness of the proposed approach for reliable testing of optimality in a wide range of stochastic optimization scenarios.

1. Lecture 4
Nonlinear Stochastic Programming
by the Monte-Carlo method
Leonidas Sakalauskas
Institute of Mathematics and Informatics
Vilnius, Lithuania <sakal@ktl.mii.lt>
EURO Working Group on Continuous Optimization

2. Content
 Stochastic unconstrained optimization
 Monte Carlo estimators
 Statistical testing of optimality
 Gradient-based stochastic algorithm
 Rule for Monte-Carlo sample size regulation
 Counterexamples
 Nonlinear stochastic constrained optimization
 Convergence Analysis
 Counterexample

3. Stochastic unconstrained
optimization
Let us consider the stochastic unconstrained
optimization problem
F ( x) Ef x, min
n
x R
-elementary event in the probability space , , Px ,
n
f :R R, - random function:
Px - the measure, defined by probability density
function:
p : Rn R

4. Monte-Carlo samples
We assume here that the Monte-Carlo samples of a
certain size N are provided for any x R n
Y ( y1, y 2 ,..., y N ),
the sampling estimator of the objective function
N
1
F ( x) f ( x, y j )
N j 1
and sampling variance can be computed
N
2 1 j
2
D ( x) f ( x, y ) F ( x)
N 1 j 1

5. Gradient
Assume the stochastic gradient is evaluated using
the same random sample:
N
1 j
g ( x) g ( x, y ),
N j 1

6. Covariance matrix
and the sampling covariance matrix is computed as
well
N
1 j j
T
A( x) g x, y g x g x, y g x
N n j 1

7. Gradient search procedure
0 n
Let some initial point x be given and the
random sample of a certain initial size N0 be generated at
this point, as well as, the Monte-Carlo estimates be
computed.
The iterative stochastic procedure of gradient search can
be used further:
x t 1
x t ~( x t )
g

8. Monte-Carlo sample size problem
There is no a great necessity to compute
estimators with a high accuracy on starting the
optimisation, because then it suffices only to
approximately evaluate the direction leading to
the optimum.
Therefore, one can obtain not so large samples at
the beginning of the optimum search and, later
on, increase the size of samples so as to get the
estimate of the objective function with a desired
accuracy just at the time of decision making on
finding the solution to the optimisation problem.

9. Monte-Carlo sample size problem
The following version for regulating the
sample size is proposed:
n Fish( , n, N t n)
Nt 1
min max ~ t T t 1 ~ t n, N min , N max
(G ( x ) ( A( x )) (G ( x )

10. Statistical testing of the optimality
hypothesis
The optimality hypothesis could be accepted for some
point x t with significance
1
if the following condition is satisfied
(N t n) (G ( x t ))T ( A( x t )) 1
(G ( x t ))
Tt 2 Fish( , n, N t n)
n

11. Statistical testing of the optimality
hypothesis
Next, we can use the asymptotic normality again and
decide that the objective function is estimated with a
permissible accuracy , if its confidence bound does
not exceed this value:
~ t
D( x ) / N t

12. Importance sampling
Let consider an application of SP to
estimation of probabilities of rare events:
t2 ( t a )2 (t a )2 t2
1 2
1 2 2 2
P( x ) e dt e e e dt
2 x 2 x
a2 t 2 t2
1 at
2 2
1 2
e dt g (a , t ) e dt
2 x a 2 x a
a2
at
where: g (a , t ) e 2

13. Importance sampling
Assume a be the parameter that should
be chosen.
The second moment is :
t2 t2
2 1 2 2
1 2 at a 2
2
D ( x, a) g (a , t ) e dt e dt
2 x a 2 x a
a2 t 2 a2 t2
1 at
2 2
e 2
e dt e dt
2 x 2 x a

14. Importance sampling
Assume a be the parameter that should
be chosen.
The second moment is :
t2 t2
2 1 2 2
1 2 at a 2
2
D ( x, a) g (a , t ) e dt e dt
2 x a 2 x a
a2 t 2 a2 t2
1 at
2 2
e 2
e dt e dt
2 x 2 x a

15. Importance sampling
Select the parameter a in order to minimize
the variance:
1,20
1,00
0,80
2 2
2 D ( x, a) P ( x) 0,60
P( x ) P 2 ( x ) 0,40
0,20
0,00
0,00 2,00 4,00 6,00 8,00
a

16. Importance sampling
~
Pt
t at Sample size
(%) P( x ) 2.86650x10 -7
1 5.000 1000 16.377 2.48182x10-7
2 5.092 51219 2.059 2.87169x10-7
3 5.097 217154 1.000 2.87010x10-7

17. Manpower-planning problem
The employer must decide upon a base
level of regular staff at various skill levels.
The recourse actions available are regular
staff overtime or outside temporary help in
order to meet unknown demand of service
at minimum cost (Ermolyev and Wets
(1988)).

18. Manpower-planning problem
x j : base level of regular staff at skill level j = 1, 2, 3
y j ,t : amount of overtime help
z j ,t : amount of temporary help,
cj : cost of regular staff at skill level j = 1, 2, 3
qj : cost of overtime,
rj : cost of temporary help
wt : demand of services at period t,
t : absentees rate for regular staff at time t,
ratio of amount of skill level j per amount of
j 1 : j-1 required,

19. Manpower-planning problem
The problem is to choose the number of staff
on three levels x ( x1 , x2 , x3 ) in order to
minimize the expected costs:
3 12 3
F ( x, z ) cj xj E min ( (q j y j , t rj z j ,t ))
j 1 t 1 j 1
s.t. xj 0, y j ,t 0, z j ,t 0,
3 3
(y j ,t z j ,t ) wt t xj , t 1, 2, , 12,
j 1 j 1
y j ,t 0.2 t xj, j 1, 2, 3, t 1, 2, , 12,
j 1 (x j yj 1, t zj 1, t ) (x j yj 1, t zj 1, t ) 0, j 1, 2, 3, t 1, 2, , 12.
the demands are normal: N( t, 2
) , t l t
t

20. X 12
3
Manpower-planning problem
Manpower amount and costs in USD
with confidence interval 100 USD
l x1 x2 x3 F
0 9222 5533 1106 94.899
1 9222 5533 1106 94.899
10 9376 5616 1106 96.832
30 9452 5672 1036 96.614

21. Nonlinear Stochastic Programming
 Constrained continuous (nonlinear )stochastic
programming problem is in general
F0 ( x) Ef 0 x, f 0 ( x, z ) p ( z )dz min
Rn
F1 ( x) Ef1 x, f1 ( x, z ) p ( z )dz 0,
Rn
n
x .

22. Nonlinear Stochastic Programming
Let us define the Lagrange function
L( x, ) F0 ( x) F1 ( x)
L( x, ) El ( x, , )
l ( x, , ) f 0 ( x, ) f1 ( x, )

23. Nonlinear Stochastic Programming
Procedure for stochastic optimization:
t 1 t ~
x x x L( x t , t
)
t 1 t ~ t ~
max[0, ( F1 ( x ) DF1 ( x t ))]
0 0 0
N , , x - initial values
- parameters of
0, 0 optimization

24. Conditions and testing of optimality
F0 ( x ) F1 ( x ) 0, F1 ( x ) 0
~ 1 ~
(N n) ( x L)' A ( x L) / n Fish( , n, N n)
~ t ~ t
F1 ( x ) DF1 ( x ) 0 2 i
DFi / N i

25. Analysis of Convergence
In general the sample size is increased
as geometric progression:
t
N
t 1
N
t i t Q
N
i 0
N
1

26. Wrap-Up and conclusions
 The approach presented in this lecture is
grounded by the termination procedure and
the rule for adaptive regulation of size of
Monte-Carlo samples, taking into account the
statistical modeling accuracy.

27. Wrap-Up and Conclusions
 The computer study shows that the approach
developed provides us the estimator for a
reliable testing of the optimality hypothesis in a
wide range of dimensionality of stochastic
optimization problem (2<n<100)
 Termination procedure proposed allows us to
test the optimality hypothesis and to evaluate
reliably the confidence intervals of the
objective and constraint functions