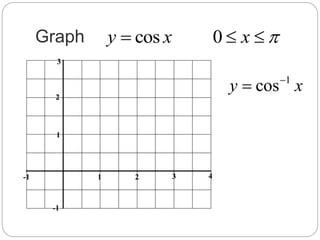
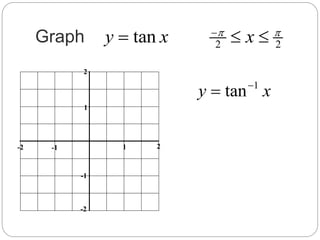
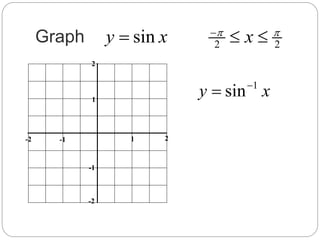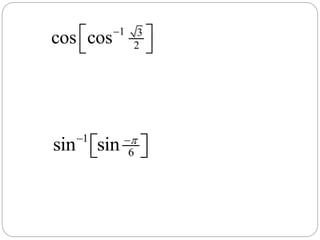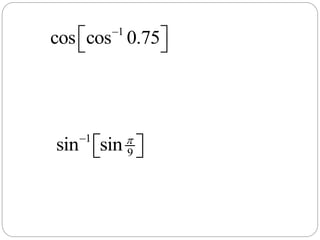This document discusses inverse trigonometric functions. It defines inverse functions as the relation obtained by interchanging the x and y values of a function. It notes that the inverse of a one-to-one function will also be a function, and the domain of a function is the range of its inverse. Graphs of the inverse sine, cosine, and tangent functions are shown between -π and π. Examples are given of evaluating inverse trigonometric functions at exact values and approximate values. Practice problems for students are listed at the end.

1. Inverse Sine, Cosine, and Tangent
Functions
*One-to-One Function
6.1 Inverse Trigonometric
Functions

2. Function and One-to-One
Function One-to-one
 For each x, there is
exactly one y.
 The graph “passes”
the vertical line test.
 For each y, there is
exactly one x.
 The graph “passes”
the horizontal line
test.
 If a function is one-to-
one, the inverse will
also be a function.

3. Inverse -
 The relation obtained by interchanging the x and
y values of a function.
 The inverse of a function that is NOT one-to-one
can be made a function by limiting the domain of
the original function to make it one-to-one.
 The domain of a function is the range of its
inverse.
 The range of a function is the domain of its
inverse.

4. Graph 2 2siny x x 
  
-2 -1
2
1
-2
-1
21
1
siny x


5. Graph cos 0y x x   
-1 4321
3
-1
2
1
1
cosy x


6. Graph 2 2tany x x 
  
-2 -1
2
1
-2
-1
21
1
tany x


7. Evaluate – exact value
 1 1
2sin

8. Evaluate – exact value
 1 2
2sin 

9. Evaluate – exact value
 1
cos 0

10. Evaluate – exact value
 1 1
2cos


11. Evaluate – exact value
 1
tan 1

12. Evaluate – exact value
 1
tan 3


13. Evaluate - approximation
1
sin 0.37
 1
cos 0.82

 1
tan 4.21

0.38
2.53
1.34 

14. 1 3
2cos cos
 
 
1
6sin sin  
  

15. 1
cos cos 0.75
  
1
9sin sin 
  

16. p. 457 # 1 - 4, 13 - 44
Assignment