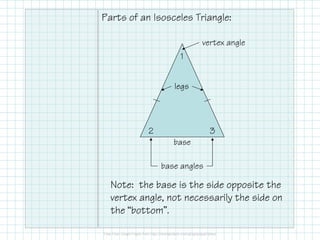
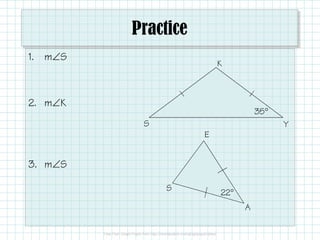
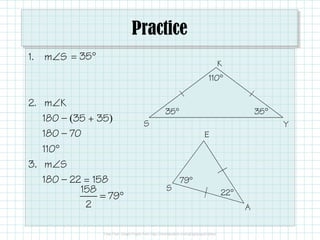
The document covers properties and theorems related to isosceles and equilateral triangles, including the isosceles triangle theorem and its converse, as well as the equilateral triangle corollary. It explains how to identify these triangles by their side lengths and angle measures, and provides practice problems to reinforce the concepts. Additionally, it clarifies terminology, such as identifying the base and vertex angles of isosceles triangles.

1. Isosceles and Equilateral Triangles
The student is able to (I can):
• Identify isosceles and equilateral triangles by side length
and angle measureand angle measure
• Use the Isosceles Triangle Theorem to solve problems
• Use the Equilateral Triangle Corollary to solve problems

2. Parts of an Isosceles Triangle:
1
legs
vertex angle
2 3
base
base angles
Note: the base is the side opposite the
vertex angle, not necessarily the side on
the “bottom”.

3. Isosceles
Triangle
Theorem
If two sides of a triangle are congruent,
then the angles opposite the sides are
congruent.
C
B
A
AB CB A C≅ ⇒ ∠ ≅ ∠
Converse of
the Isosceles
Triangle
Theorem
If two angles of a triangle are congruent,
then the sides opposite those angles are
congruent.
F
E
D
D F DE FE∠ ≅ ∠ ⇒ ≅

4. Equilateral
Triangle
Corollary
Converse of
If a triangle is equilateral, then it is
equiangular.
If a triangle is equiangular, then it is
C
B
A
AB BC CA
A B C
≅ ≅
⇒ ∠ ≅ ∠ ≅ ∠
Converse of
the Equilateral
Triangle
Corollary
If a triangle is equiangular, then it is
equilateral.
D E F
DE EF FD
∠ ≅ ∠ ≅ ∠
⇒ ≅ ≅
F
E
D

5. Practice
1. m∠S
2. m∠K
35°
S
K
Y
3. m∠S
S Y
S
E
A
22°

6. Practice
1. m∠S
2. m∠K
180 — (35 + 35)
35°
S
K
Y
= 35°
35°
110°
180 — (35 + 35)
180 — 70
110°
3. m∠S
180 — 22 = 158
S Y
S
E
A
22°= °
158
79
2
79°