This document provides information on wave quantum mechanics and electron configurations. It discusses:
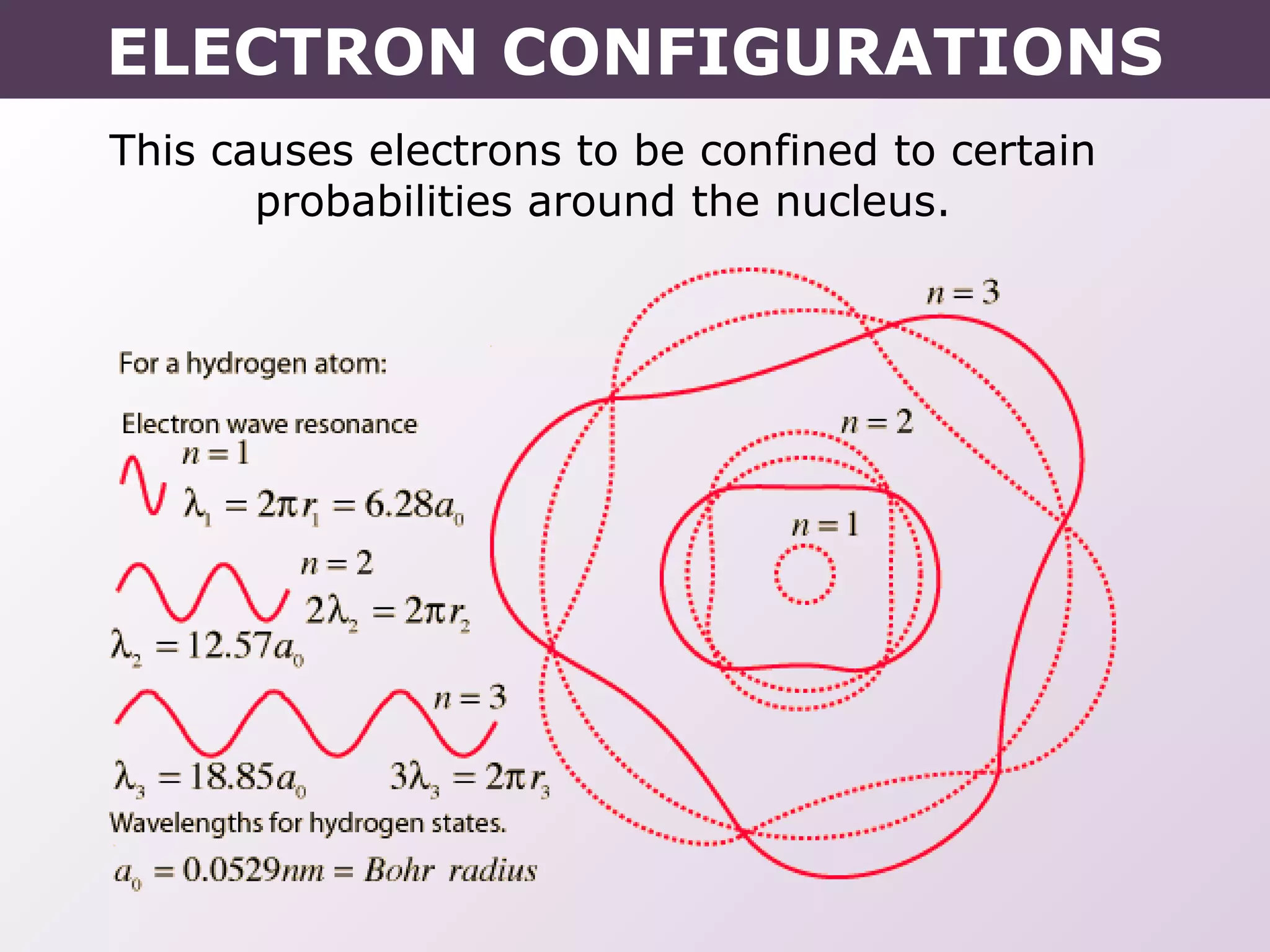
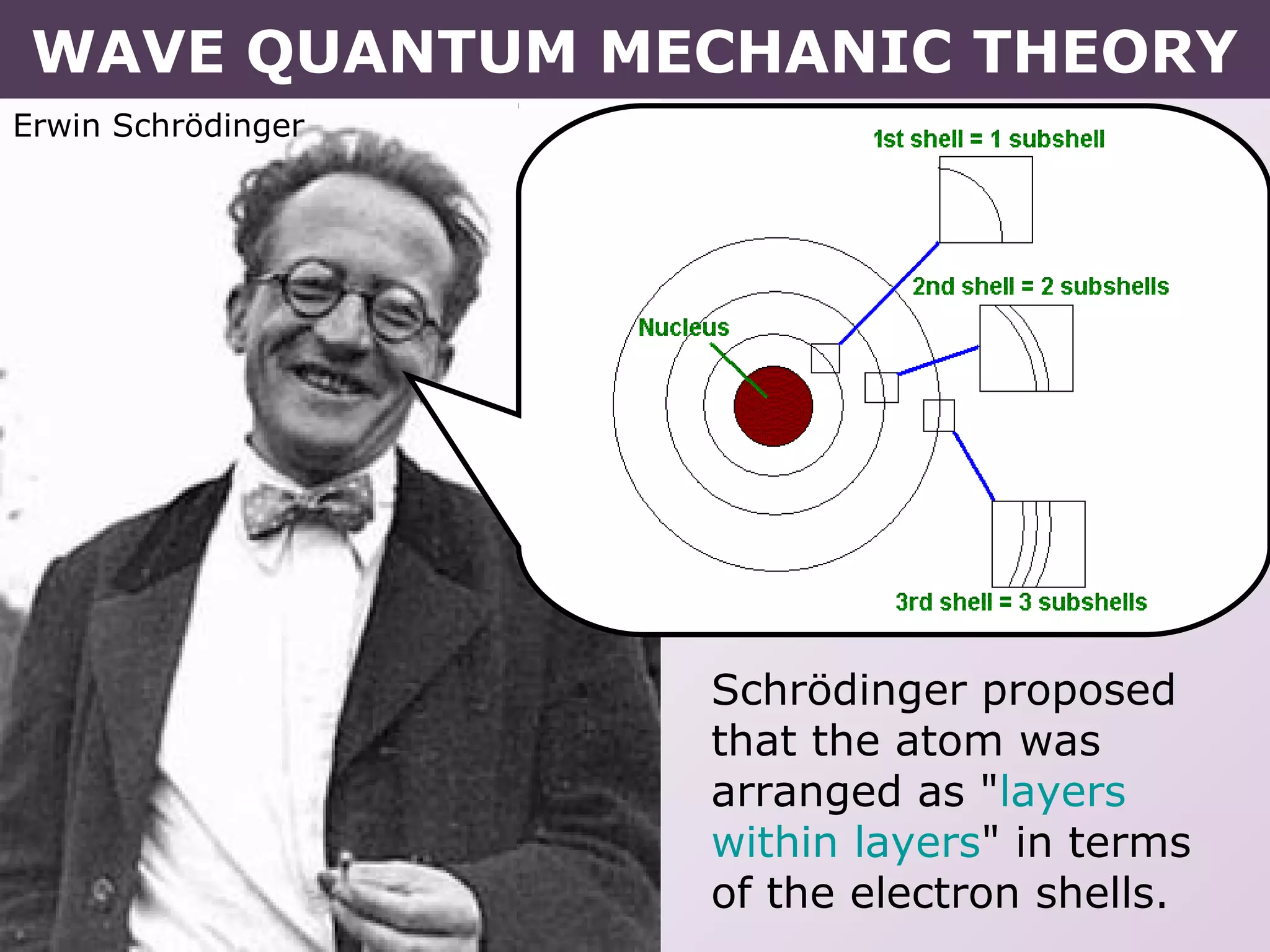
- Erwin Schrodinger's contributions to developing quantum mechanics and proposing the wave-like nature of electrons.
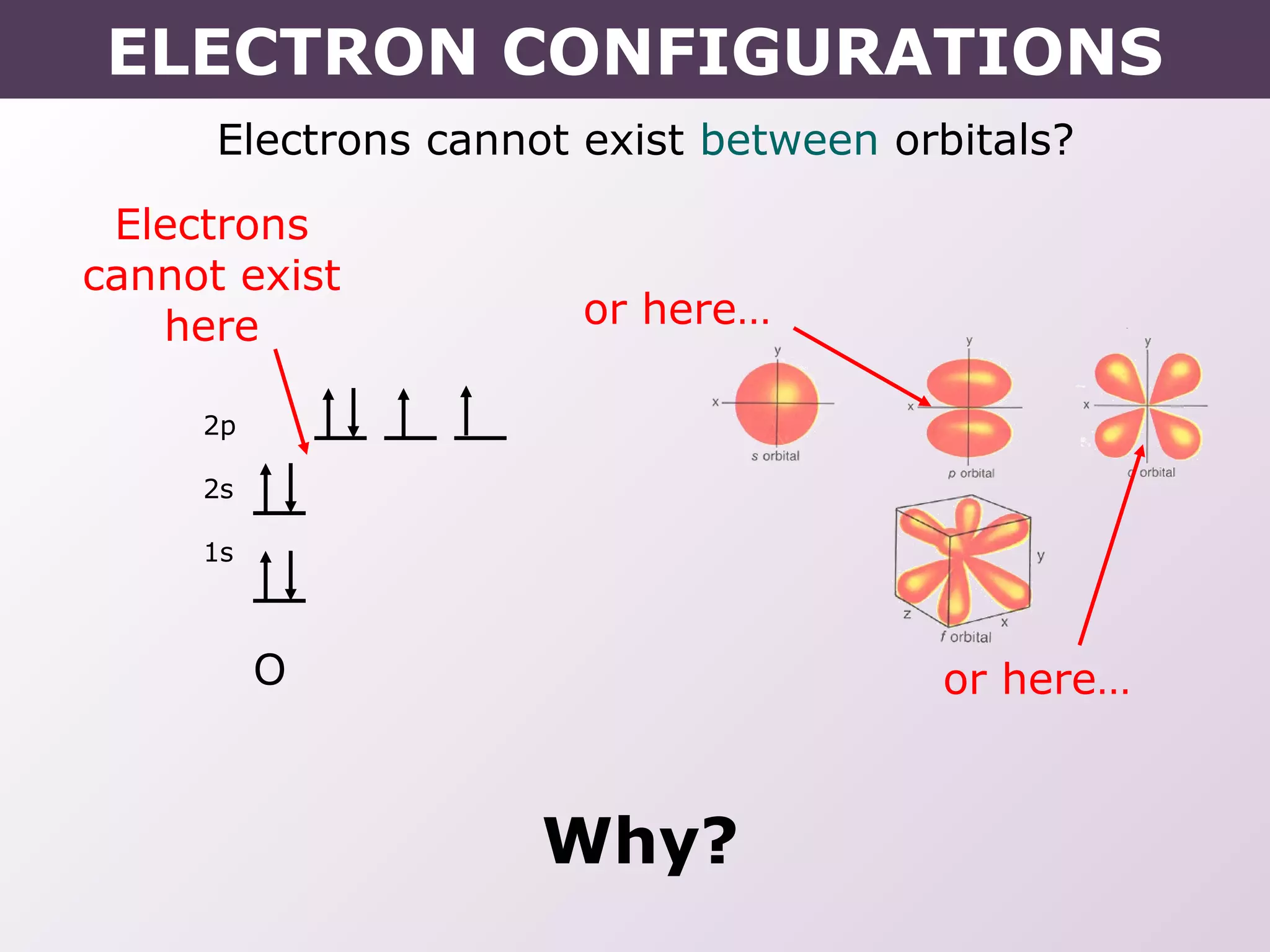
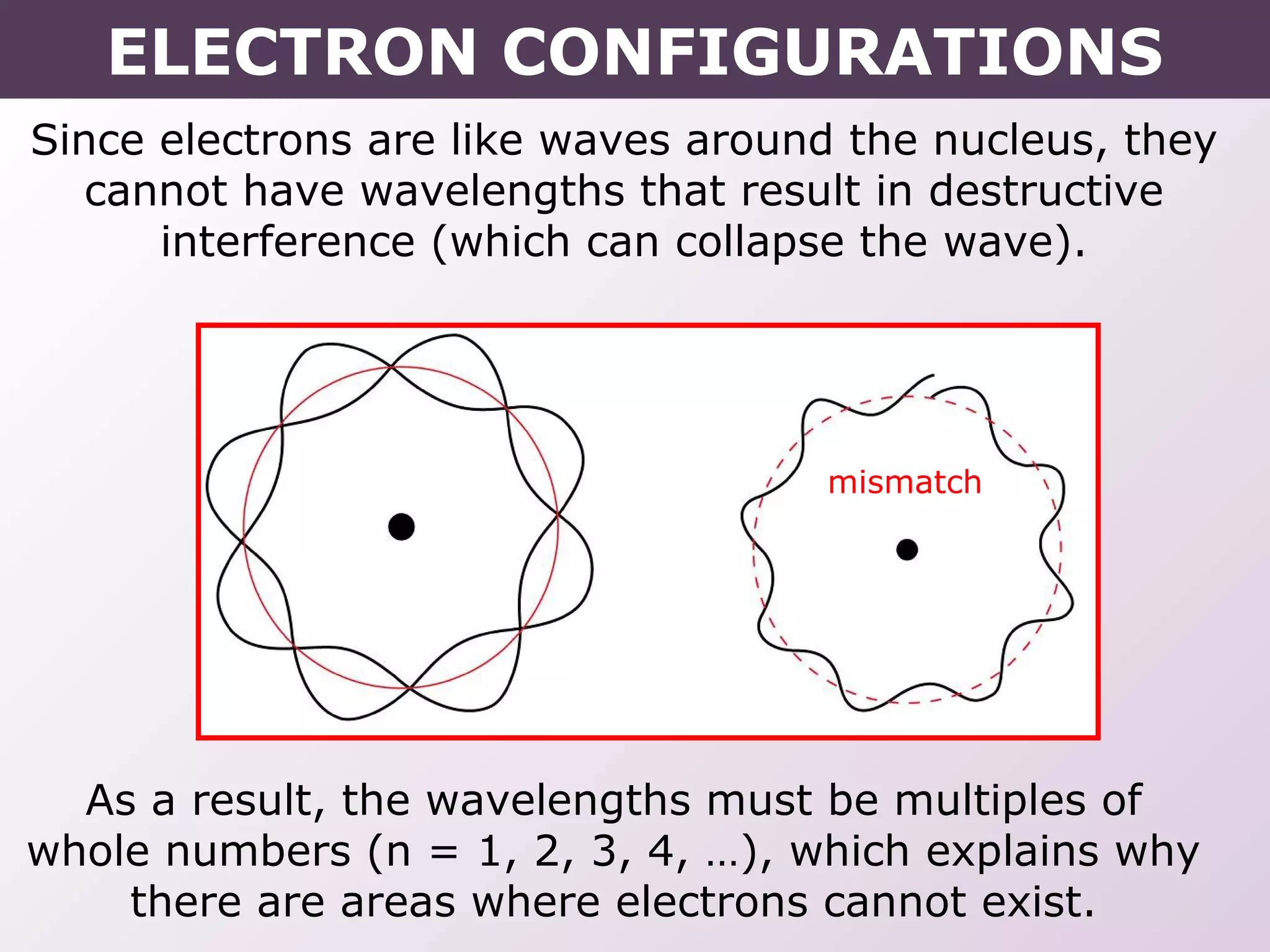
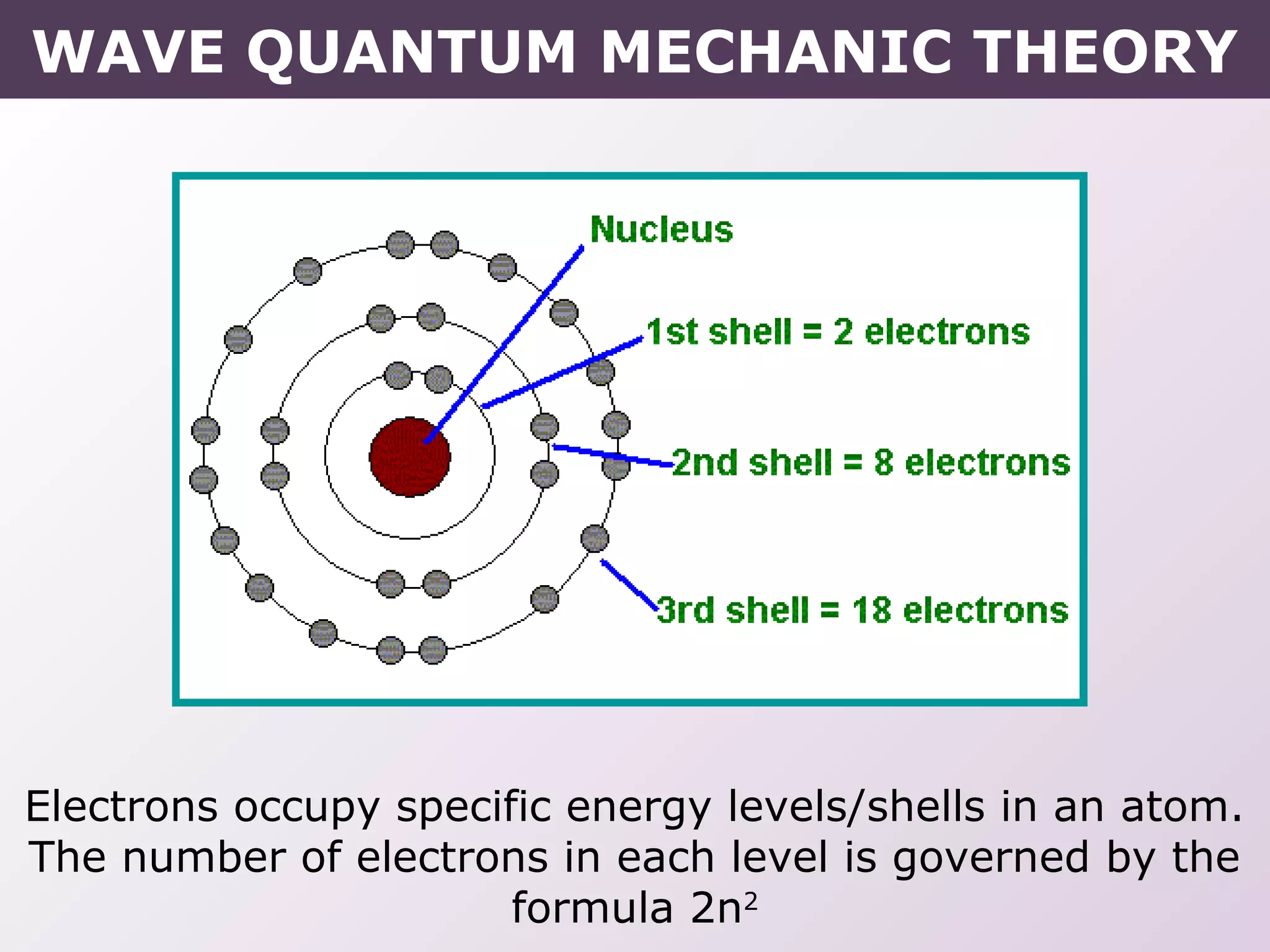
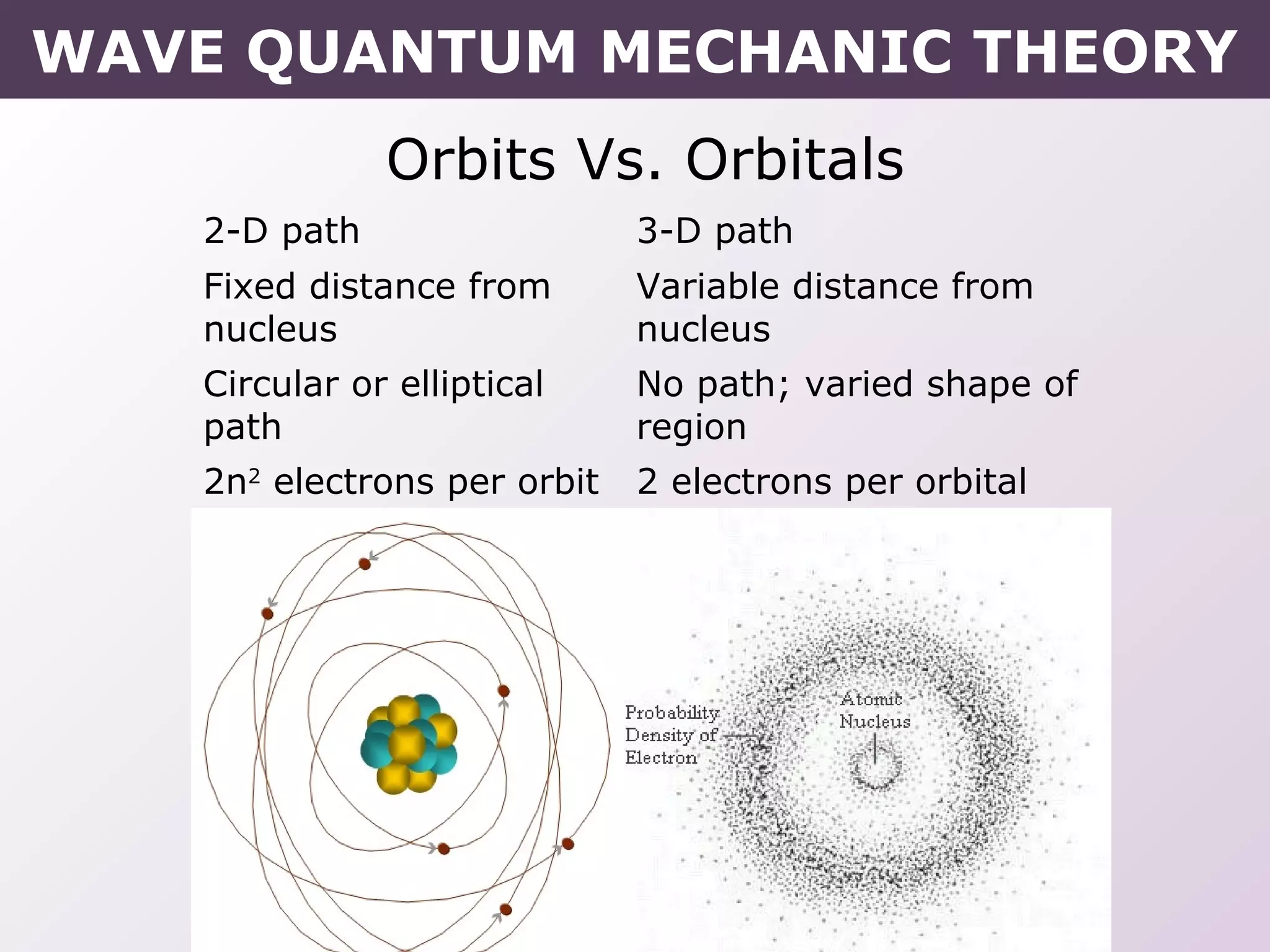
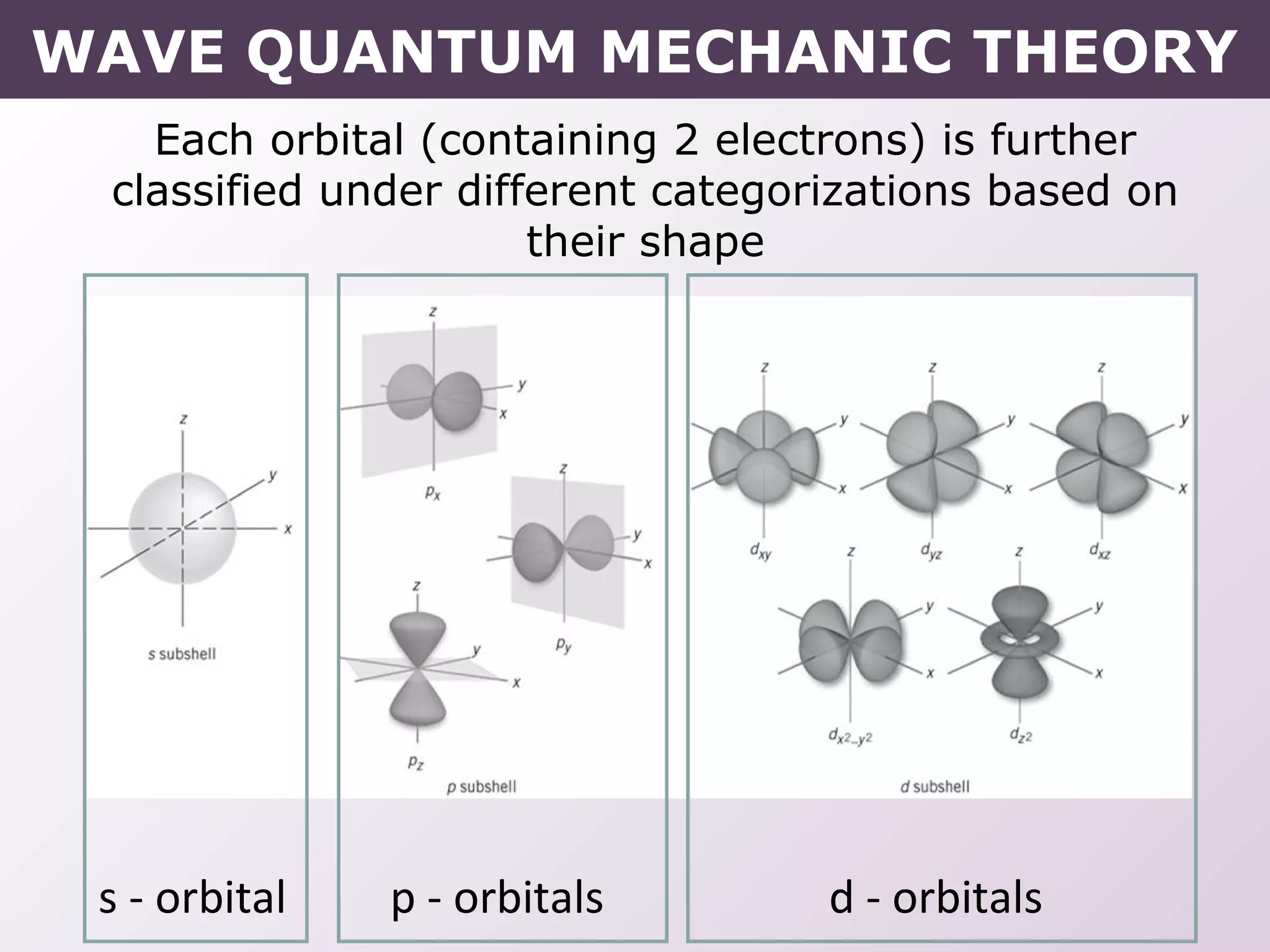
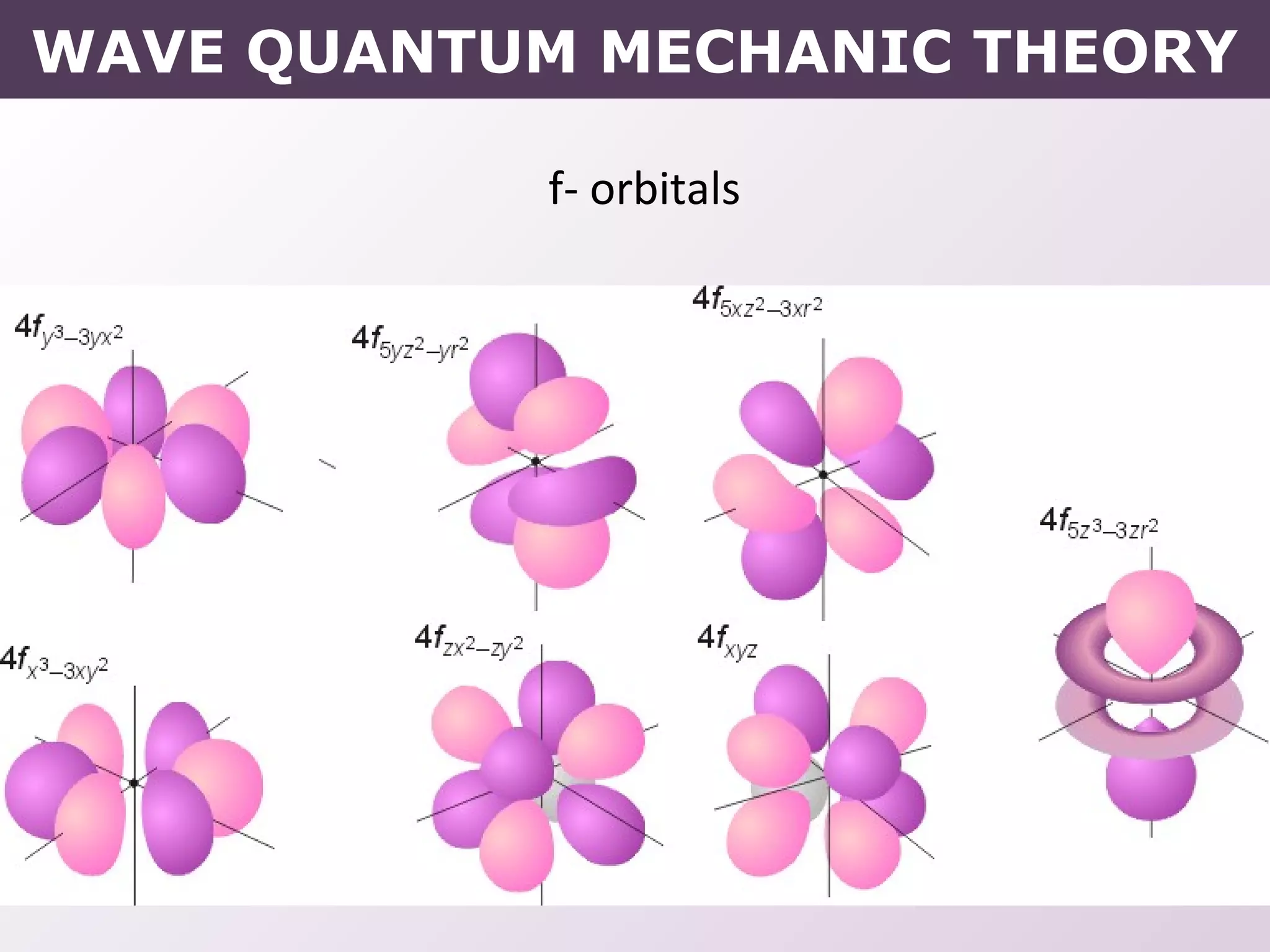
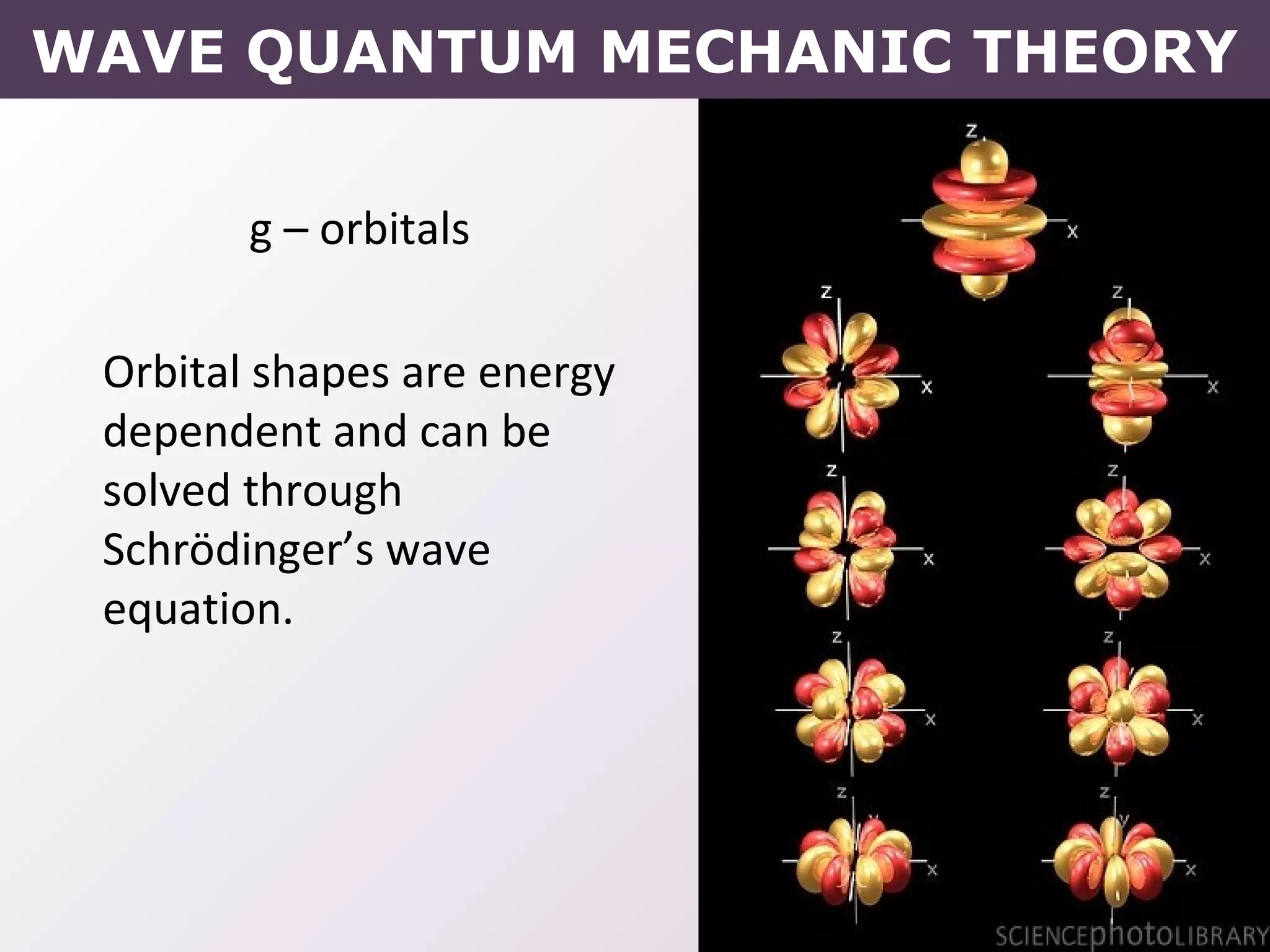
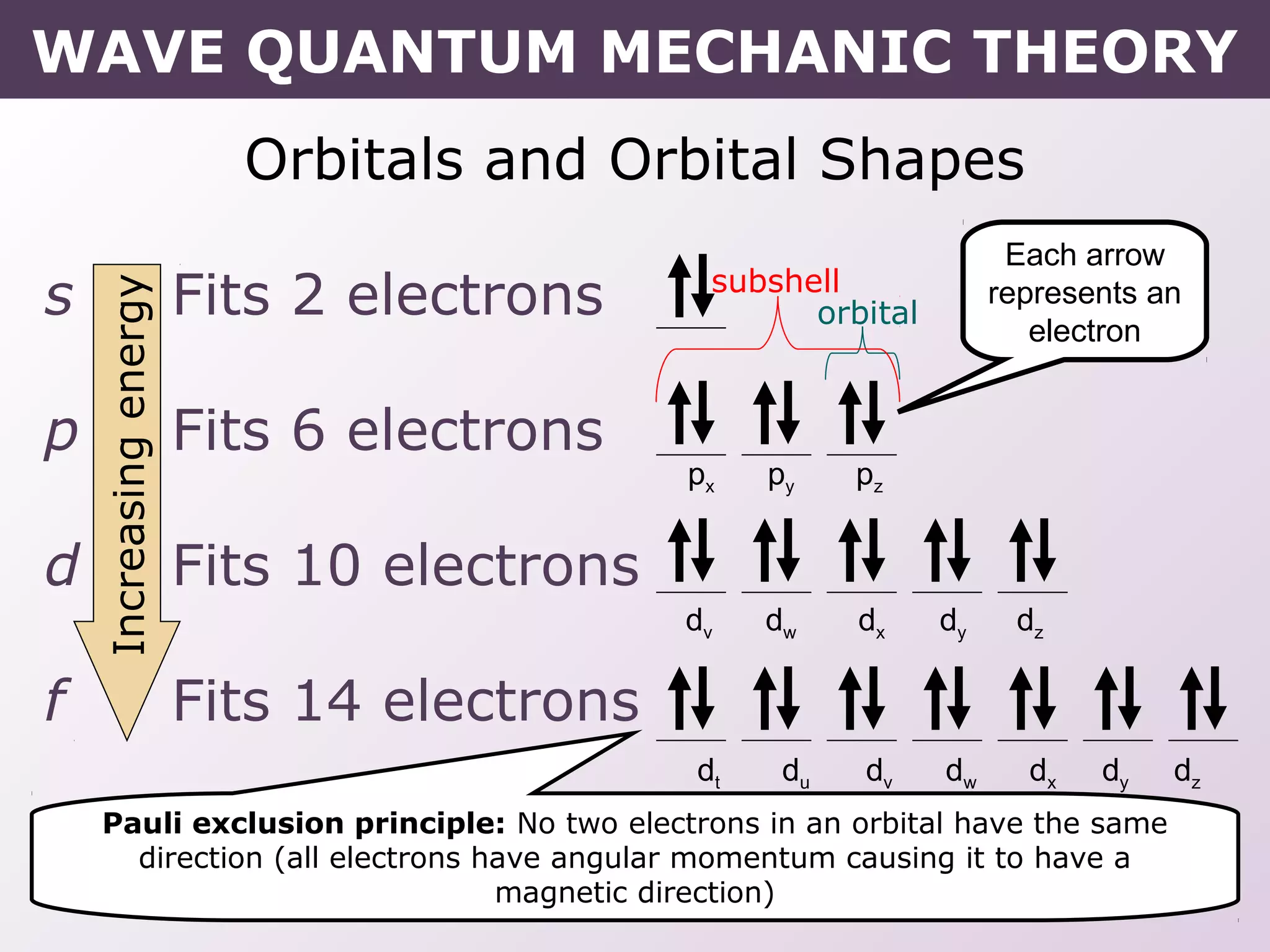
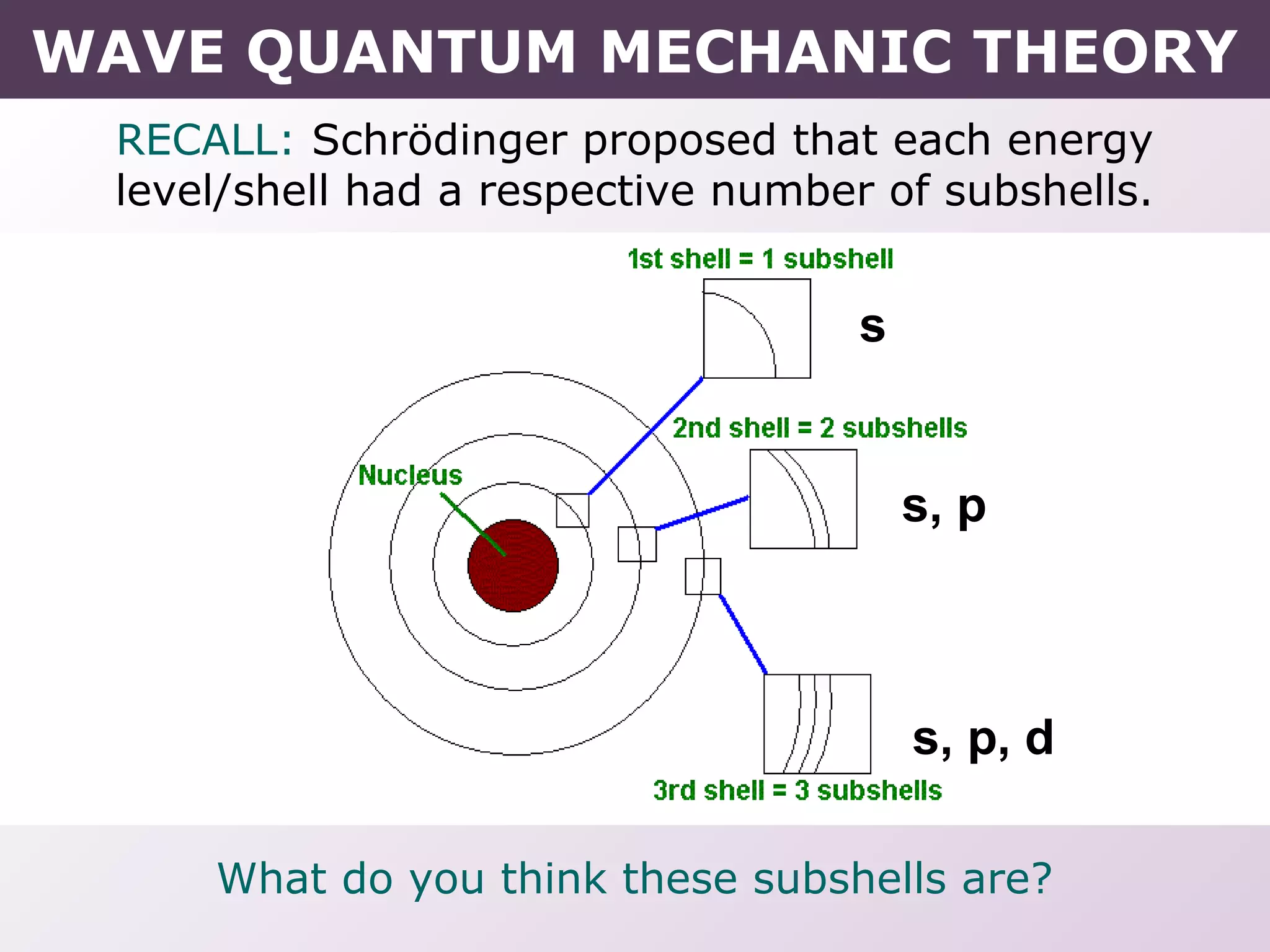
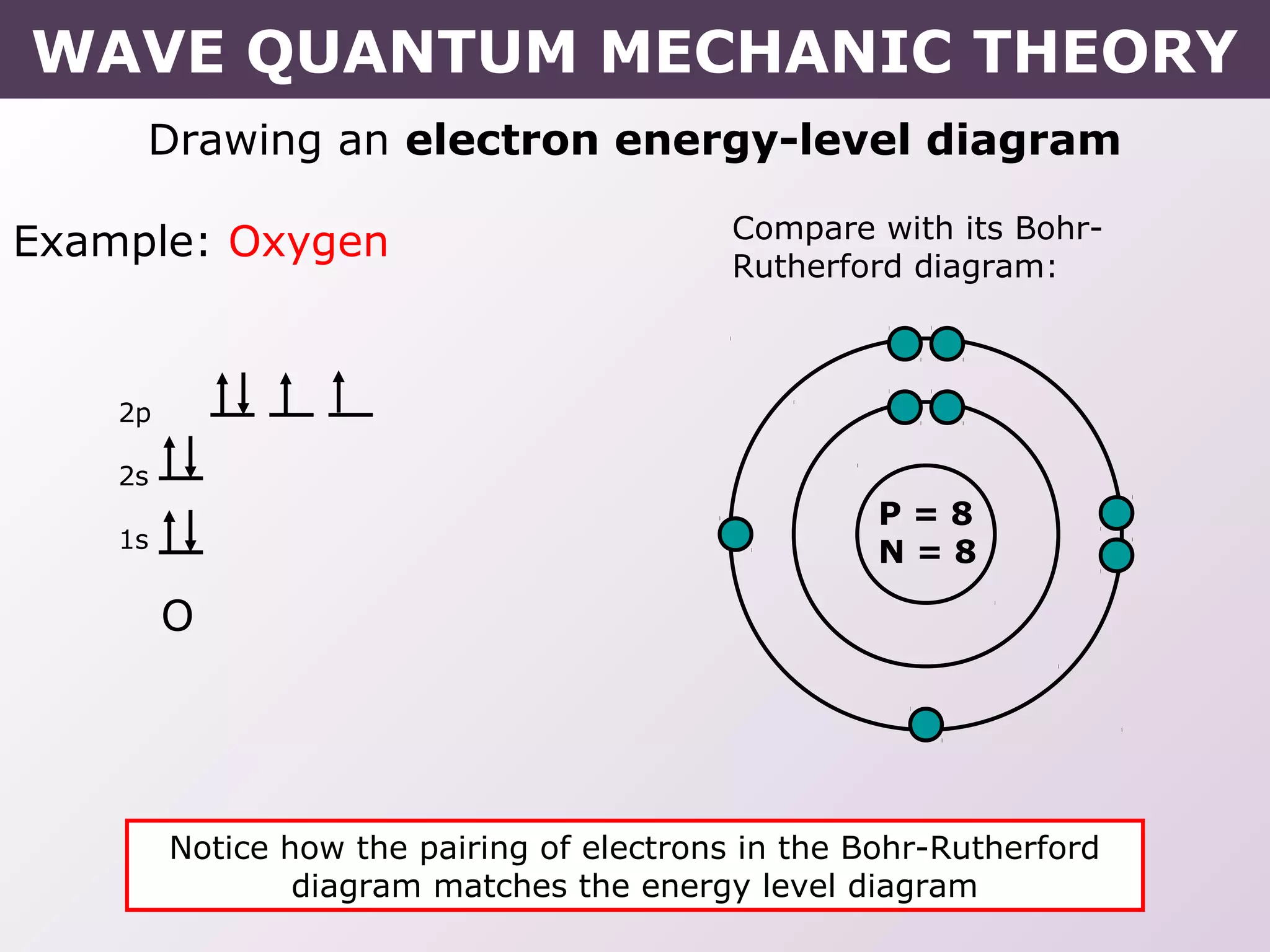
- How electrons occupy distinct energy levels and orbitals around the nucleus, with specific shapes defined by Schrodinger's wave equation.
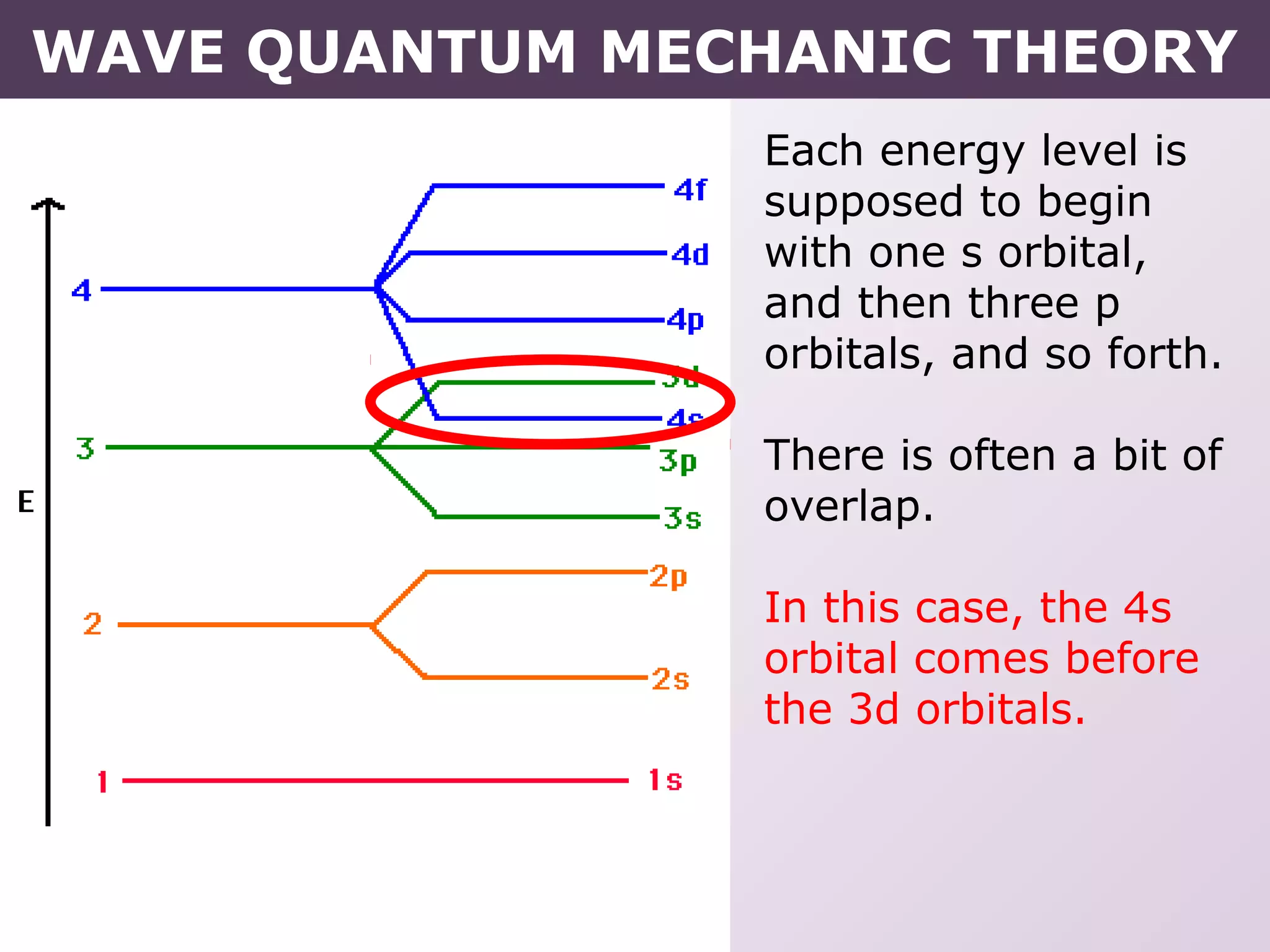
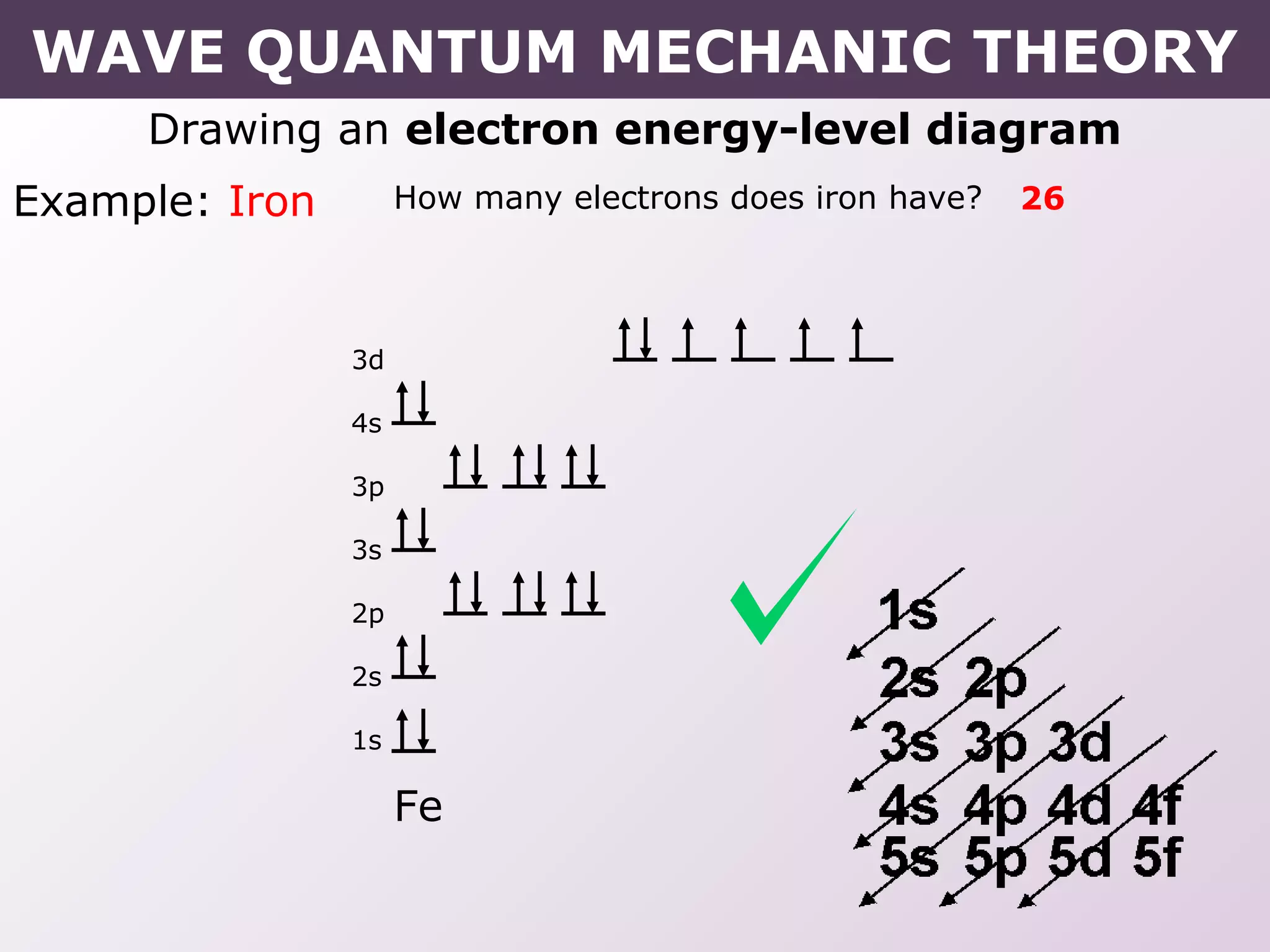
- Rules for building up electron configurations, including Hund's rule and the Aufbau principle for filling orbitals in order of increasing energy.
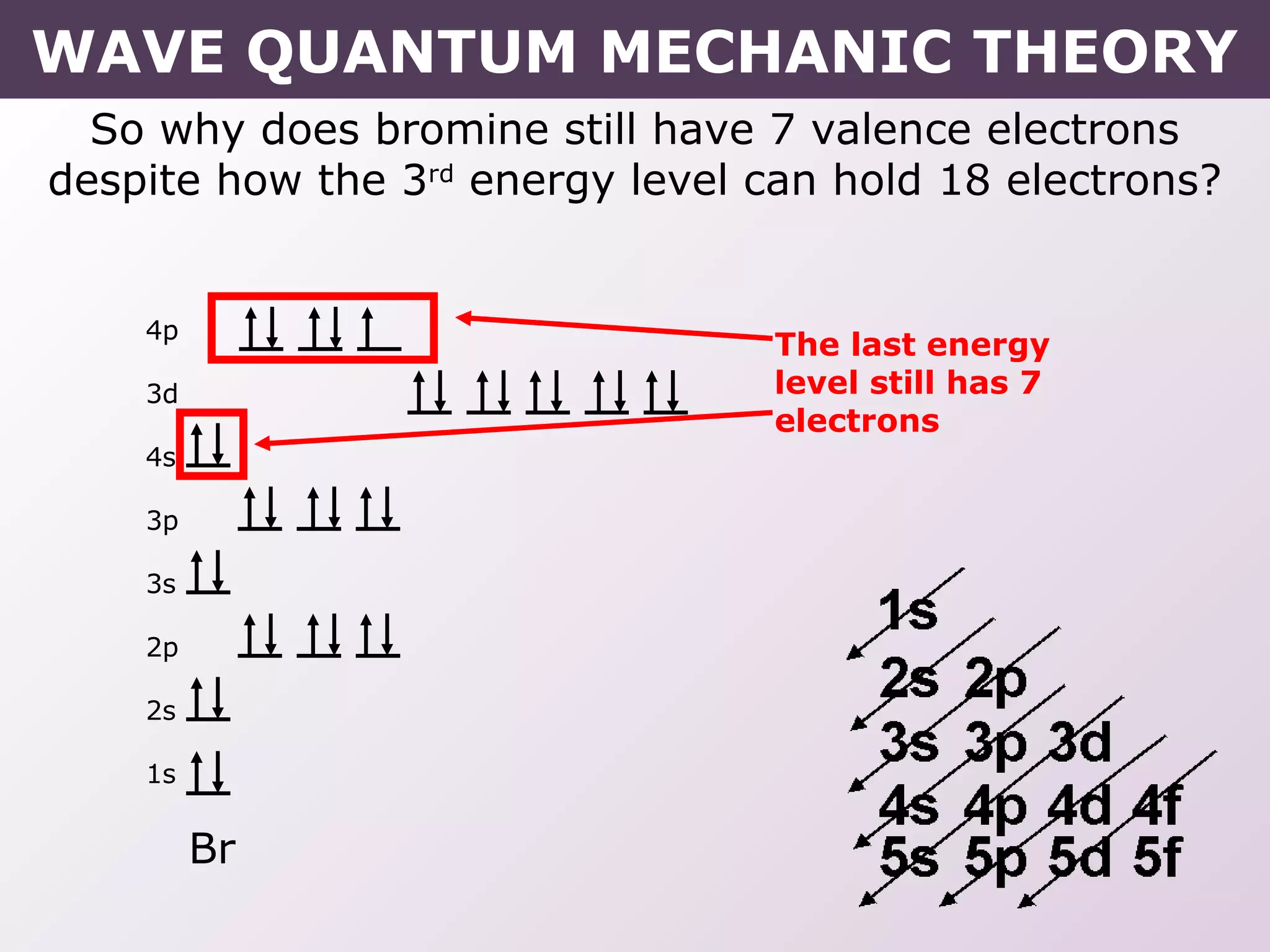
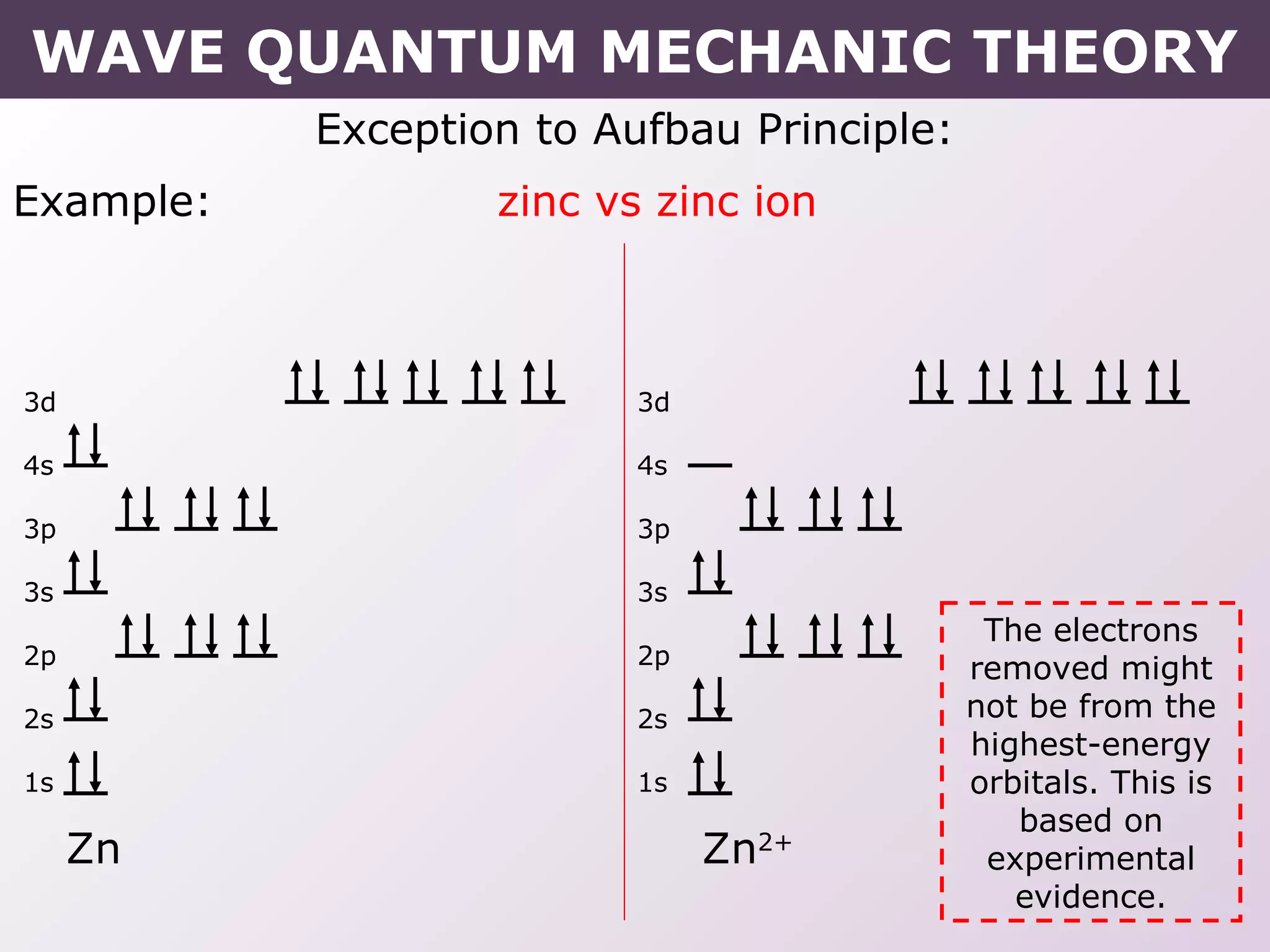
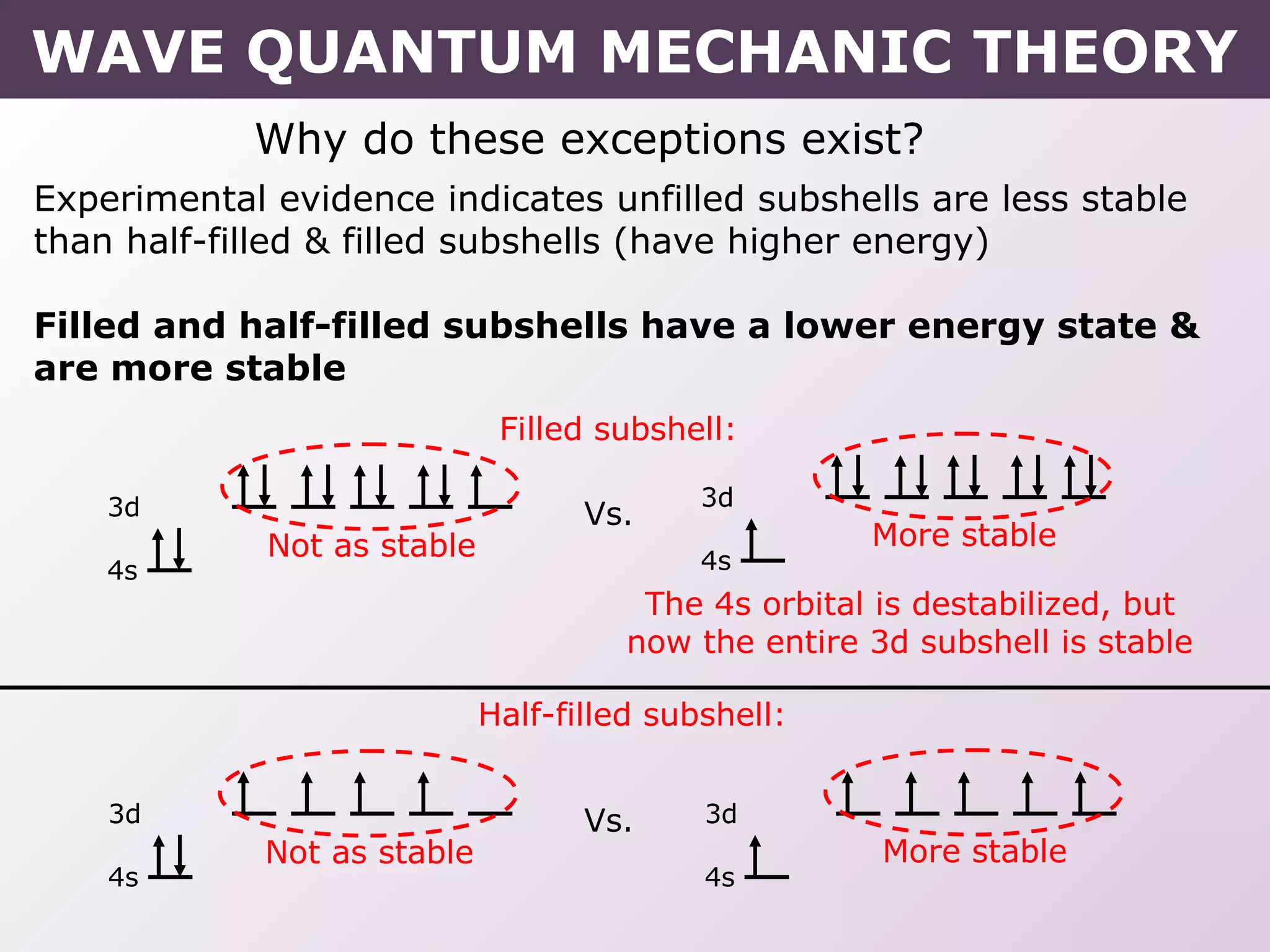
- Exceptions to the Aufbau principle seen in some transition metals where half or fully filled subshells are more stable.
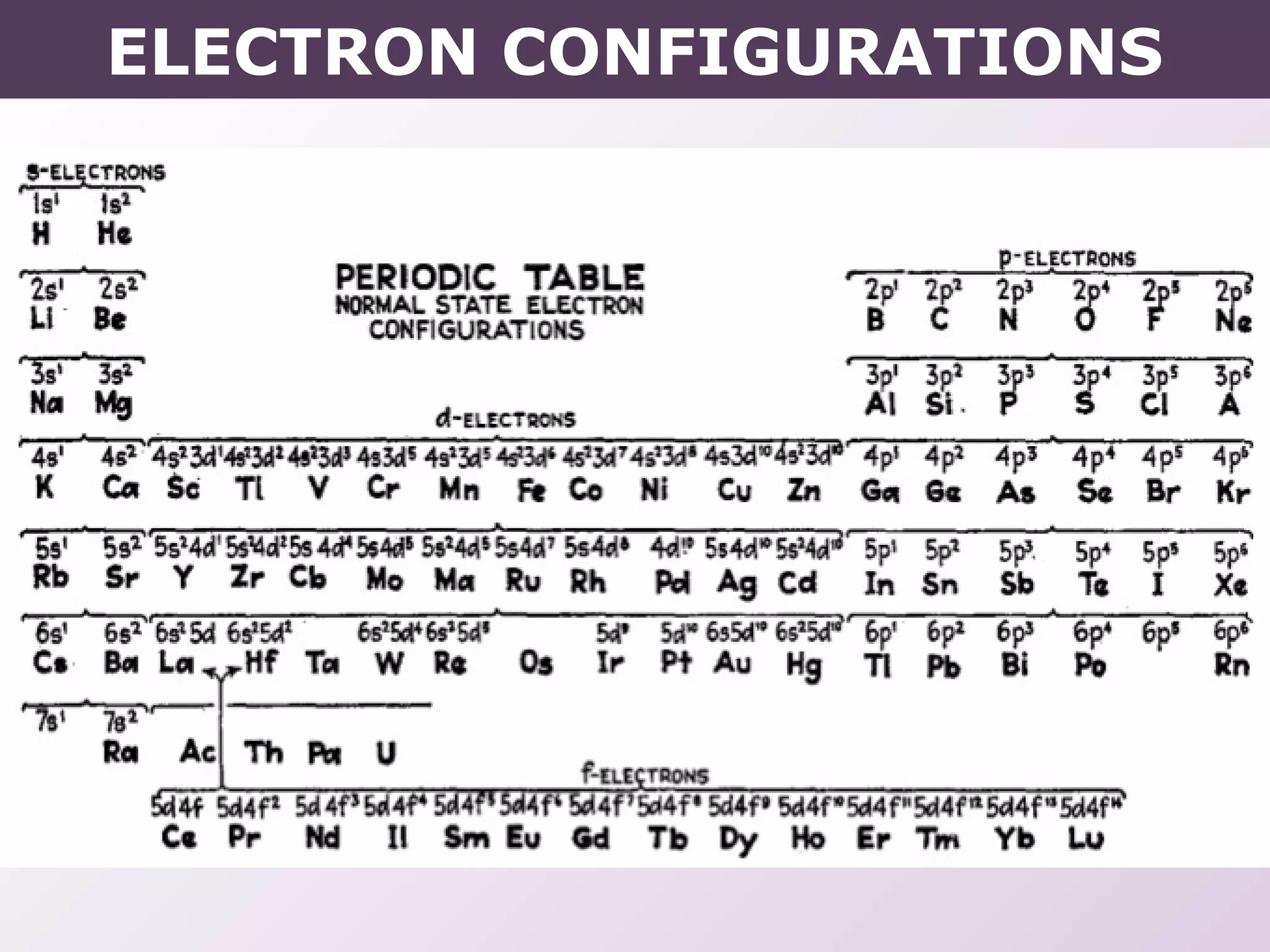
- How electron configurations are written using shorthand notation based on noble gas cores.



















![Writing Electron Configurations
Shorthand form of Electron configurations:
Cl: 1s2
2s2
2p6
3s2
3p5
Sn: 1s2
2s2
2p6
3s2
3p6
4s2
3d10
4p6
5s2
4d10
5p2
Cl: [Ne] 3s2
3p5
Sn: [Kr] 5s2
4d10
5p2
Same configuration as Neon
Same configuration as krypton
In the shorthand version, the “core electrons” of an
atom are represented by the preceding noble gas
ELECTRON CONFIGURATIONS](https://image.slidesharecdn.com/tang02-wavequantummechanicmodel-150908172700-lva1-app6892/75/Tang-02-wave-quantum-mechanic-model-38-2048.jpg)
![Explaining multivalent metals:
Electrons are lost to achieve stability:
Cd: [Kr]5s2
4d10
becomes Cd2+
We can now explain why some transition metals can form
multiple ions:
Pb: [Xe]6s2
4f14
5d10
6p2
becomes Pb2+
or Pb4+
Fe: [Ar]4s2
3d6
becomes Fe2+
or Fe3+
3d
4s
3d
4s
ELECTRON CONFIGURATIONS](https://image.slidesharecdn.com/tang02-wavequantummechanicmodel-150908172700-lva1-app6892/75/Tang-02-wave-quantum-mechanic-model-41-2048.jpg)