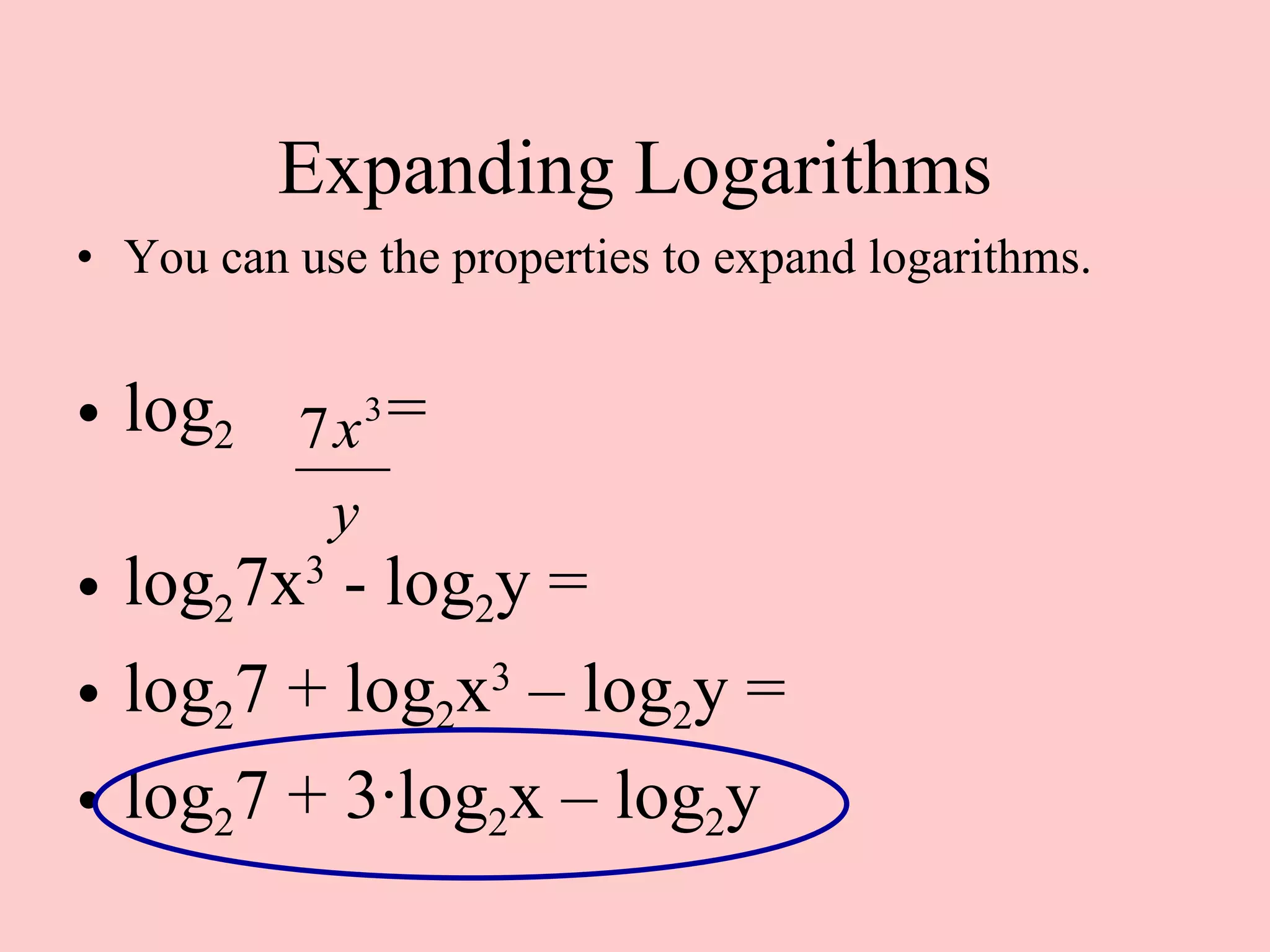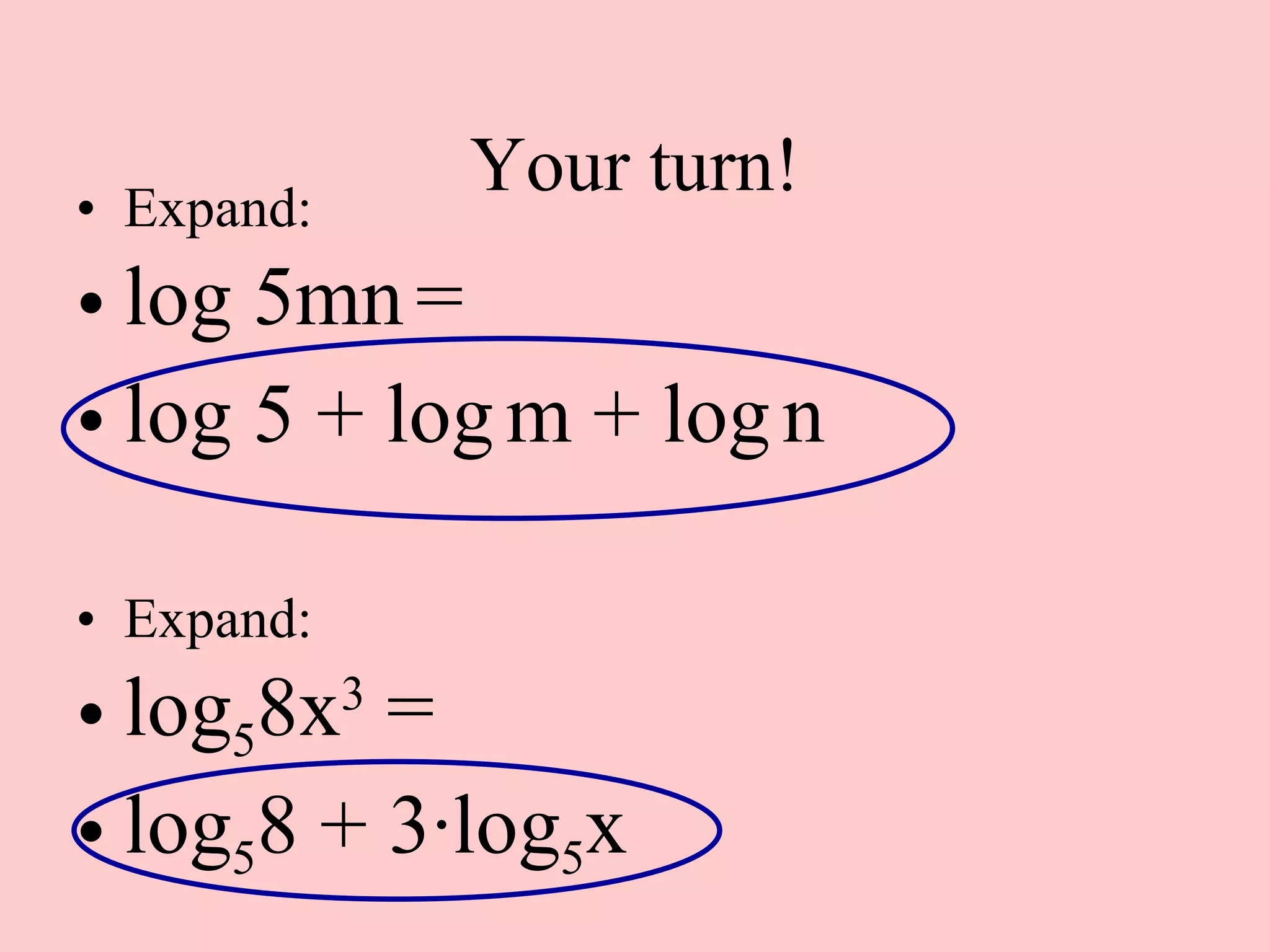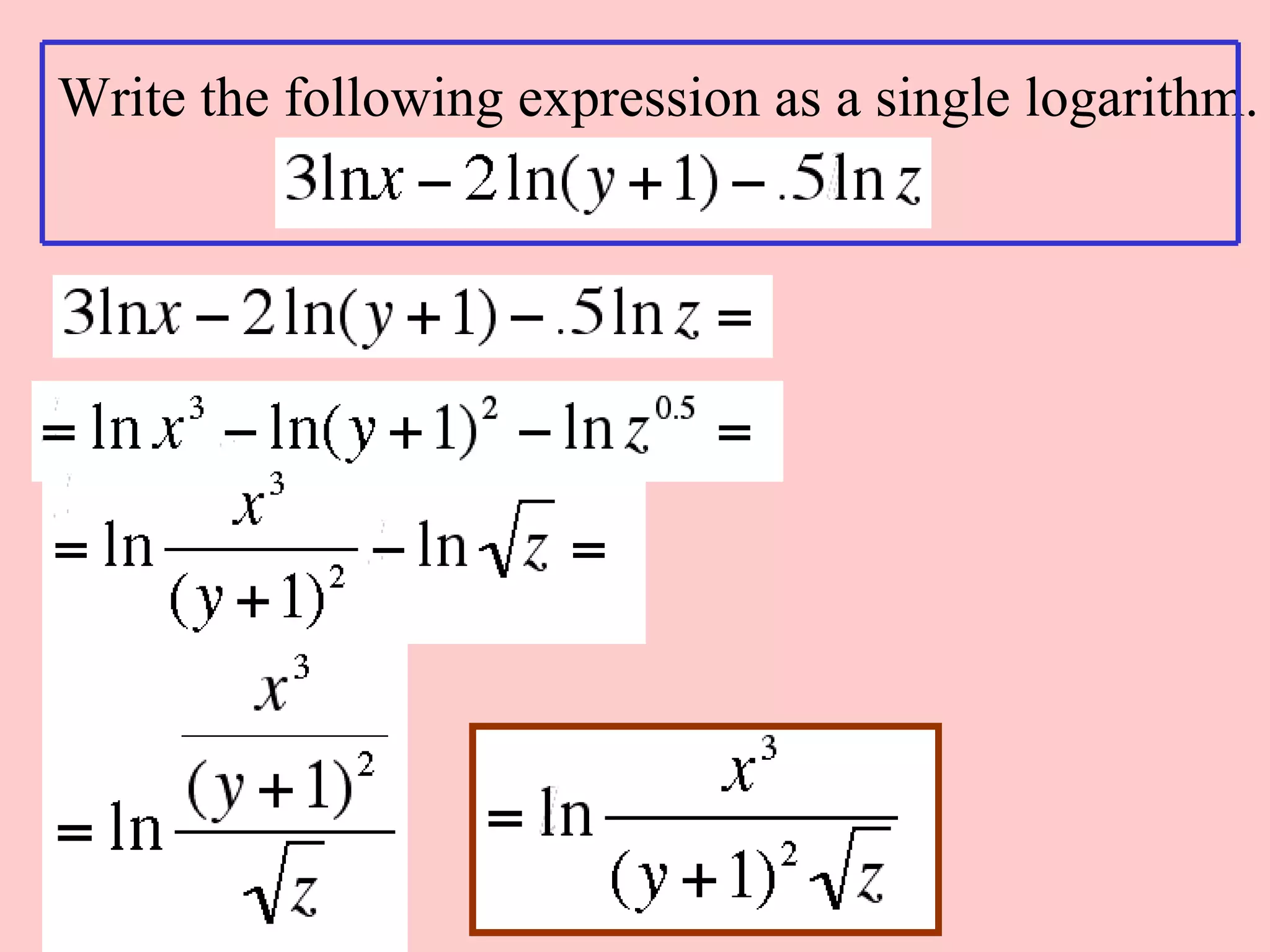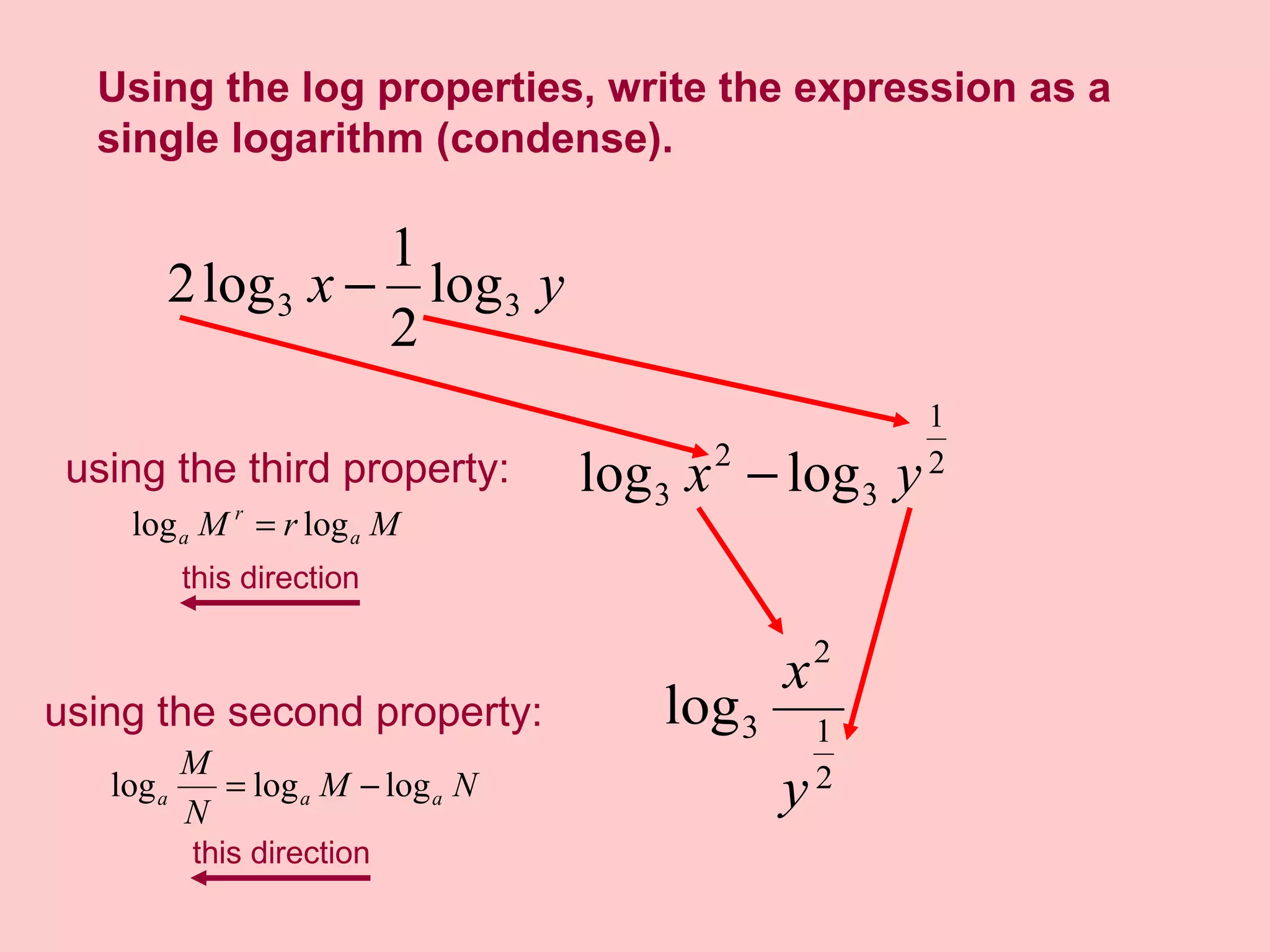
This document discusses properties of logarithms, including: 1) Logarithms with the same base "undo" each other according to the inverse function relationship between logarithms and exponents. 2) Logarithmic expressions can be expanded using properties to write them as sums or differences of individual logarithmic terms, or condensed into a single logarithm. 3) The change of base formula allows converting between logarithms with different bases, with common uses being to change to base 10 or the base of natural logarithms.

1. Properties of Logarithms

2. Since logs and exponentials of the same base are inverse functions of each other they “undo” each other. Remember that: This means that: inverses “undo” each each other = 5 = 7

3. CONDENSED EXPANDED Properties of Logarithms = = = = (these properties are based on rules of exponents since logs = exponents) 3. 2. 1.

4. Using the log properties, write the expression as a sum and/or difference of logs (expand). using the second property: When working with logs, re-write any radicals as rational exponents. using the first property: using the third property:

5. Using the log properties, write the expression as a single logarithm (condense). using the third property: using the second property: this direction this direction

6. Use log 5 3 ≈.683 and log 5 7≈1.209 Approximate: log 5 3/7 = log 5 3 – log 5 7 ≈ .683 – 1.209 = -.526 log 5 21 = log 5 (3 ·7)= log 5 3 + log 5 7≈ .683 + 1.209 = 1.892

7. Use log 5 3 ≈.683 and log 5 7≈1.209 Approximate: log 5 49 = log 5 7 2 = 2 log 5 7 ≈ 2(1.209)= 2.418

8. Expanding Logarithms You can use the properties to expand logarithms. log 2 = log 2 7x 3 - log 2 y = log 2 7 + log 2 x 3 – log 2 y = log 2 7 + 3 · log 2 x – log 2 y

9. Your turn! Expand: log 5mn = log 5 + log m + log n Expand: log 5 8x 3 = log 5 8 + 3 · log 5 x

10. Condensing Logarithms log 6 + 2 log2 – log 3 = log 6 + log 2 2 – log 3 = log (6 ·2 2 ) – log 3 = log = log 8

11. Write the following expression as a single logarithm.

12. Your turn again! Condense: log 5 7 + 3 · log 5 t = log 5 7t 3 Condense: 3log 2 x – (log 2 4 + log 2 y)= log 2

13. More Properties of Logarithms This one says if you have an equation, you can take the log of both sides and the equality still holds. This one says if you have an equation and each side has a log of the same base , you know the "stuff" you are taking the logs of are equal.

14. (2 to the what is 8?) (2 to the what is 16?) (2 to the what is 10?) There is an answer to this and it must be more than 3 but less than 4, but we can't do this one in our head. Let's put it equal to x and we'll solve for x . Change to exponential form. use log property & take log of both sides (we'll use common log) use 3rd log property solve for x by dividing by log 2 use calculator to approximate Check by putting 2 3.32 in your calculator (we rounded so it won't be exact)

15. Common and Natural Logarithms

16. Change of Base Formula The 2 bases we are most able to calculate logarithms for are base 10 and base e. These are the only bases that our calculators have buttons for. For ease of computing a logarithm, we may want to switch from one base to another. The new base, a, can be any integer>1, but we often let a=10 or a=e. (We know how to calculate common logs and natural logs!)

17. Common Logarithms A common logarithm has a base of 10. If there is no base given explicitly, it is common. You can easily find common logs of powers of ten. You can use your calculator to evaluate common logs.

18. Change of base formula: u, b, and c are positive numbers with b ≠1 and c≠1. Then: log c u = log c u = (base 10) log c u = (base e)

19. Compute What is the log, base 5, of 29? Does this answer make sense? What power would you raise 5 to, to get 29? A little more than 2! (5 squared is 25, so we would expect the answer to be slightly more than 2.)

20. Use the Change-of-Base Formula and a calculator to approximate the logarithm. Round your answer to three decimal places. Since 3 2 = 9 and 3 3 = 27, our answer of what exponent to put on 3 to get it to equal 16 will be something between 2 and 3. put in calculator

21. Example Find log 6 8 using common logarithms. Solution: First, we let a = 10, b = 6, and M = 8. Then we substitute into the change-of-base formula:

22. Example We can also use base e for a conversion. Find log 6 8 using natural logarithms. Solution: Substituting e for a, 6 for b and 8 for M , we have

23. Examples: Use the change of base to evaluate: log 3 7 = (base 10) log 7 ≈ log 3 1.771 (base e) ln 7 ≈ ln 3 1.771

24. Solving equations Use the properties we have learned about exponential & logarithmic expressions to solve equations that have these expressions in them. Find values of x that will make the logarithmic or exponential equation true. For exponential equations, if the base is the same on both sides of the equation, the exponents must also be the same (equal!)

25. Sometimes it is easier to solve a logarithmic equation than an exponential one Any exponential equation can be rewritten as a logarithmic one, then you can apply the properties of logarithms Example: Solve:

26. SOLVE

27. SOLVE

28. Acknowledgement I wish to thank Shawna Haider from Salt Lake Community College, Utah USA for her hard work in creating this PowerPoint. www.slcc.edu Shawna has kindly given permission for this resource to be downloaded from www.mathxtc.com and for it to be modified to suit the Western Australian Mathematics Curriculum. Stephen Corcoran Head of Mathematics St Stephen’s School – Carramar www.ststephens.wa.edu.au

29. Change-of-Base Formula The base you change to can be any base so generally we’ll want to change to a base so we can use our calculator. That would be either base 10 or base e . “common” log base 10 “natural” log base e Example for TI-83 If we generalize the process we just did we come up with the: LOG LN