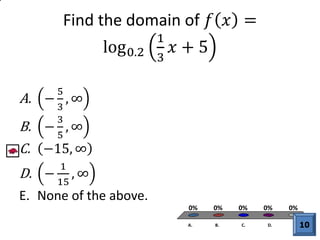
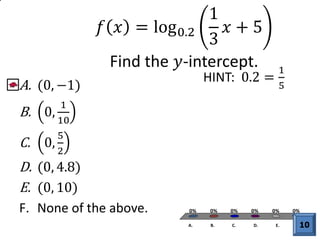
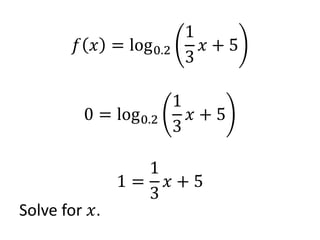The document discusses logarithmic functions, particularly focusing on their inverse relationship with exponential functions. It includes examples of finding the domain of a logarithmic function, sketching its graph, and identifying intercepts. Various methods and questions are presented related to transforming and analyzing logarithmic functions.

1. 3.3 Logarithmic Functions
Graph and apply transformations to
the graphs of logarithmic functions.
http://nicktoons.nick.com/videos/clip/stimpys-big-day-log-song-1.html

2. GRAPH AND APPLY TRANSFORMATIONS
TO THE GRAPHS OF LOGARITHMIC
FUNCTIONS.

3. An Example…
Let 푓 푥 = log0.2
1
3
푥 + 5 .
A. Find the domain of 푓.
B. Sketch the graph of 푓 by hand
and give coordinates of the 푦- and
푥- intercepts when they exist.

4. In your homework, you learned that
logarithmic functions are simply the
inverse of exponential functions. This
means that the domain of any logarithm
originates from the __________ of the
exponential function that is it’s inverse.
A. domain
B. range
C. zeros
D. discontinuities
0% 0% 0% 0%
10
A. B. C. D.

5. For any logarithmic function,
0% 0% 0% 0%
A. B. C. D.
푓 푥 = log푏 푥
the inverse function is
푓−1 푦 = 푏푦 .
What is the range of the exponential
function 푓−1 푦 = 푏푦?
A. −∞, ∞
B. −∞, 0 ∪ 0, ∞
C. 0, ∞
D. [0, ∞)
10

6. So, the domain of
푓 푥 = log푏 푔 푥
is all 푥 such that…
0% 0% 0% 0% 0%
A. B. C. D. E.
A. 푔 푥 < 0
B. 푔 푥 ≥ 0
C. 푔 푥 ≠ 0
D. 푔 푥 > 0
E. None of the above.
10

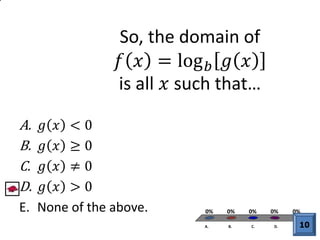
7. We know that when
푓 푥 = log푏 [푔 푥 ] ,
the domain is all 푥
such that 푔 푥 > 0.
Back to our problem…
푓 푥 = log0.2
1
3
푥 + 5
1
3
푥 + 5 > 0
Solve for 푥 to find the
domain of 푓.

8. Find the domain of 푓 푥 =
0% 0% 0% 0% 0%
A. B. C. D. E.
log0.2
1
3
푥 + 5
A. −
5
3
, ∞
B. −
3
5
, ∞
C. −15, ∞
D. −
1
15
, ∞
E. None of the above.
10

9. An Example…
Let 푓 푥 = log0.2
1
3
푥 + 5 .
A. Find the domain of 푓.
B. Sketch the graph of 푓 by hand
and give coordinates of the 푦- and
푥- intercepts when they exist.

10. OK, so the instructions say to sketch by hand, but…
…instead we are just using the MyLabsPlus graphing
system.
First you will have to choose a tool from the palette.
Recall that we are looking for the graph of the inverse of
an exponential function.
For each plotted point, (푥, 푦) that we find on the graph of
an exponential function, we find (푦, 푥) on the graph of the
logarithmic function.

11. Which of the following is the
“Logarithm tool”?
0% 0% 0% 0%
A. B. C. D.
A.
B.
C.
D.
10

12. Actually, if you’re not sure, MyLabsPlus makes it
really easy for you!
Just hover the mouse over each tool and it will
pop up with a box that says it’s name.
Click on the tool and then click anywhere in the
coordinate plane to launch the input boxes…

13. The default values for a logarithm
function are shown in the blue
boxes to the left.
They correspond to the function
푓 푥 = log 푥
Compare this to the
transformation form of the
logarithmic function
푓 푥 = 퐶 ⋅ log푏 퐴 푥 − 퐵 + 퐷
= 퐶
= 푏
= 퐴
= 퐷 = 퐵
Check this box if 퐶 < 0.
Check this box if 퐴 < 0.

14. Write our function
0% 0% 0% 0% 0%
A. B. C. D. E.
푓 푥 = log0.2
1
3
푥 + 5
in the form
푓 푥 = 퐶 ⋅ log푏 퐴 푥 − 퐵 + 퐷.
A. 푓 푥 = log0.2
1
3
푥 − −15
B. 푓 푥 = log0.2
1
3
푥 − 15
C. 푓 푥 = log0.2
1
3
푥 − 5
D. 푓 푥 = log0.2
1
3
푥 − −5
E. None of the above. 10

15. By comparing
푓 푥 = log0.2
1
3
푥 − −15
to
푓 푥 = 퐶 ⋅ log푏 퐴 푥 − 퐵 + 퐷
we can see that
퐶 = Vertical Scale = 1
푏 = base = 0.2
퐴 = Horizontal Scale =
1
3
퐵 = Horizontal Shift = −15
퐷 = Vertical Shift = 0

16. An Example…
Let 푓 푥 = log0.2
1
3
푥 + 5 .
A. Find the domain of 푓.
B. Sketch the graph of 푓 by hand
and give coordinates of the 푦- and
푥- intercepts when they exist.

17. Finding the 푦-intercept is done the same
way for every function, including
logarithms. Which of the following is the
method that will find the 푦-intercept?
A. Set the function equal to zero and
0% 0% 0% 0% 0%
A. B. C. D. E.
solve for 푥.
B. Find 푓(0).
C. Solve for 푥. Then replace 푥 with
푓−1 푦 .
D. Apply the quadratic formula.
E. None of the above.
10

18. 푓 푥 = log0.2
1
3
푥 + 5
푓 0 = log0.2
1
3
⋅ 0 + 5
푓 0 = log0.2 5
Recall (from your homework) that log푏 푥 is
defined as the exponent we must raise 푏 to in
order to get 푥.
0.2? = 5

19. 푓 푥 = log0.2
1
3
푥 + 5
Find the 푦-intercept.
0% 0% 0% 0% 0% 0%
A. B. C. D. E. F.
A. (0, −1)
B. 0,
1
10
C. 0,
5
2
D. (0, 4.8)
E. (0, 10)
F. None of the above.
10
HINT: 0.2 =
1
5

20. An Example…
Let 푓 푥 = log0.2
1
3
푥 + 5 .
A. Find the domain of 푓.
B. Sketch the graph of 푓 by hand
and give coordinates of the 푦- and
푥- intercepts when they exist.

21. Finding the 푥-intercept is done the same
way for every function, including
logarithms. Which of the following is the
method that will find the 푥-intercept?
A. Set the function equal to zero and
0% 0% 0% 0% 0%
A. B. C. D. E.
solve for 푥.
B. Find 푓(0).
C. Solve for 푥. Then replace 푥 with
푓−1 푦 .
D. Apply the quadratic formula.
E. None of the above.
10

22. 푓 푥 = log0.2
1
3
푥 + 5
0 = log0.2
1
3
푥 + 5
Solve for 푥.

23. This is not as difficult as it might look.
Recall from your homework that
0% 0% 0% 0% 0%
A. B. C. D. E.
log푏 ? = 0
A. log푏 푏 = 0
B. log푏 0 = 0
C. log푏
1
푏
= 0
D. log푏 1 = 0
E. None of the above.
10
HINT: 푏0 =?

24. 푓 푥 = log0.2
1
3
푥 + 5
0 = log0.2
1
3
푥 + 5
1 =
1
3
푥 + 5
Solve for 푥.

25. 푓 푥 = log0.2
1
3
푥 + 5
Find the 푥-intercept.
0% 0% 0% 0% 0% 0%
A. B. C. D. E. F.
A. 18, 0
B. −
4
3
, 0
C. 2, 0
D. −15, 0
E. −12, 0
F. None of the above.
10