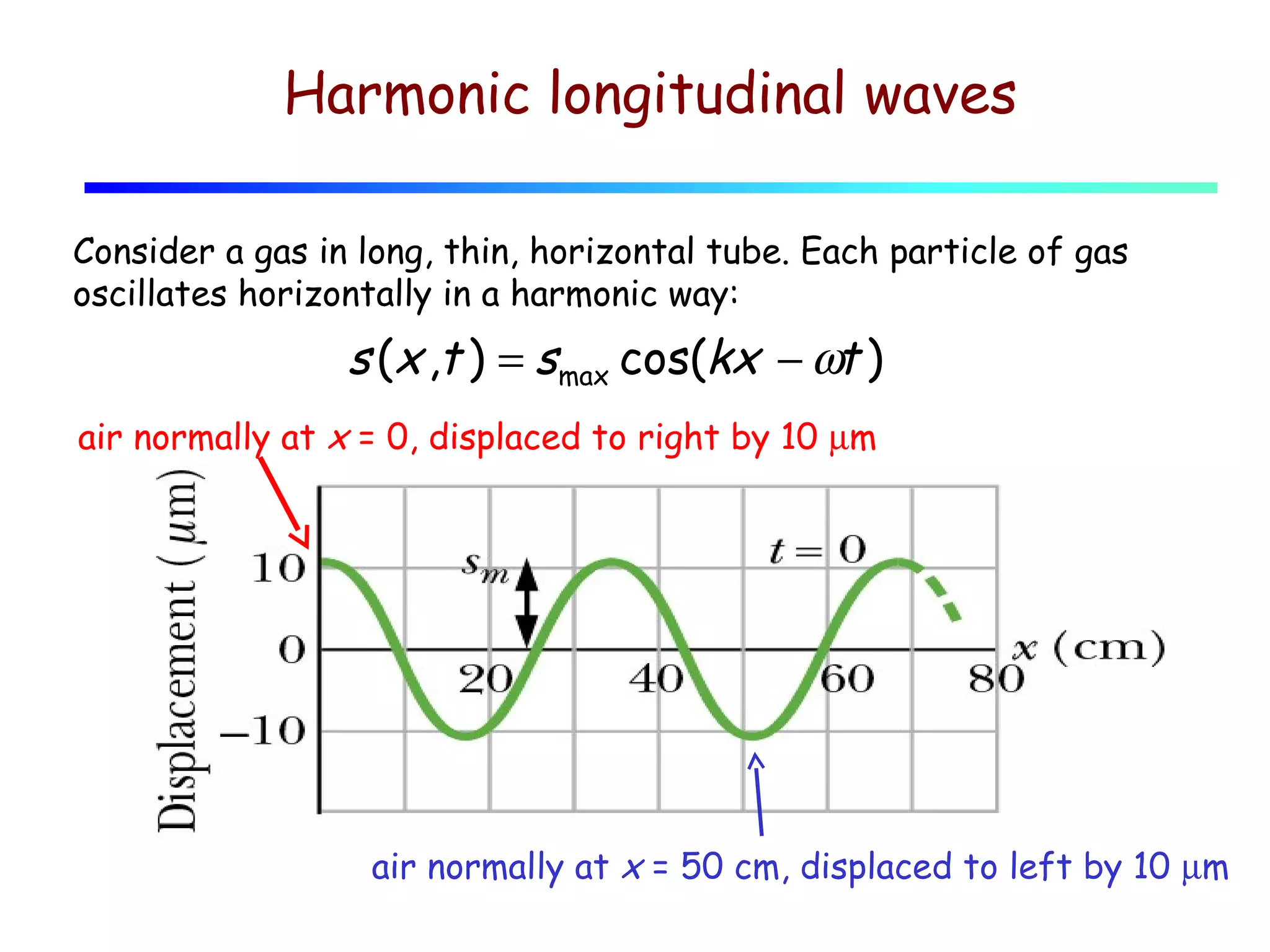
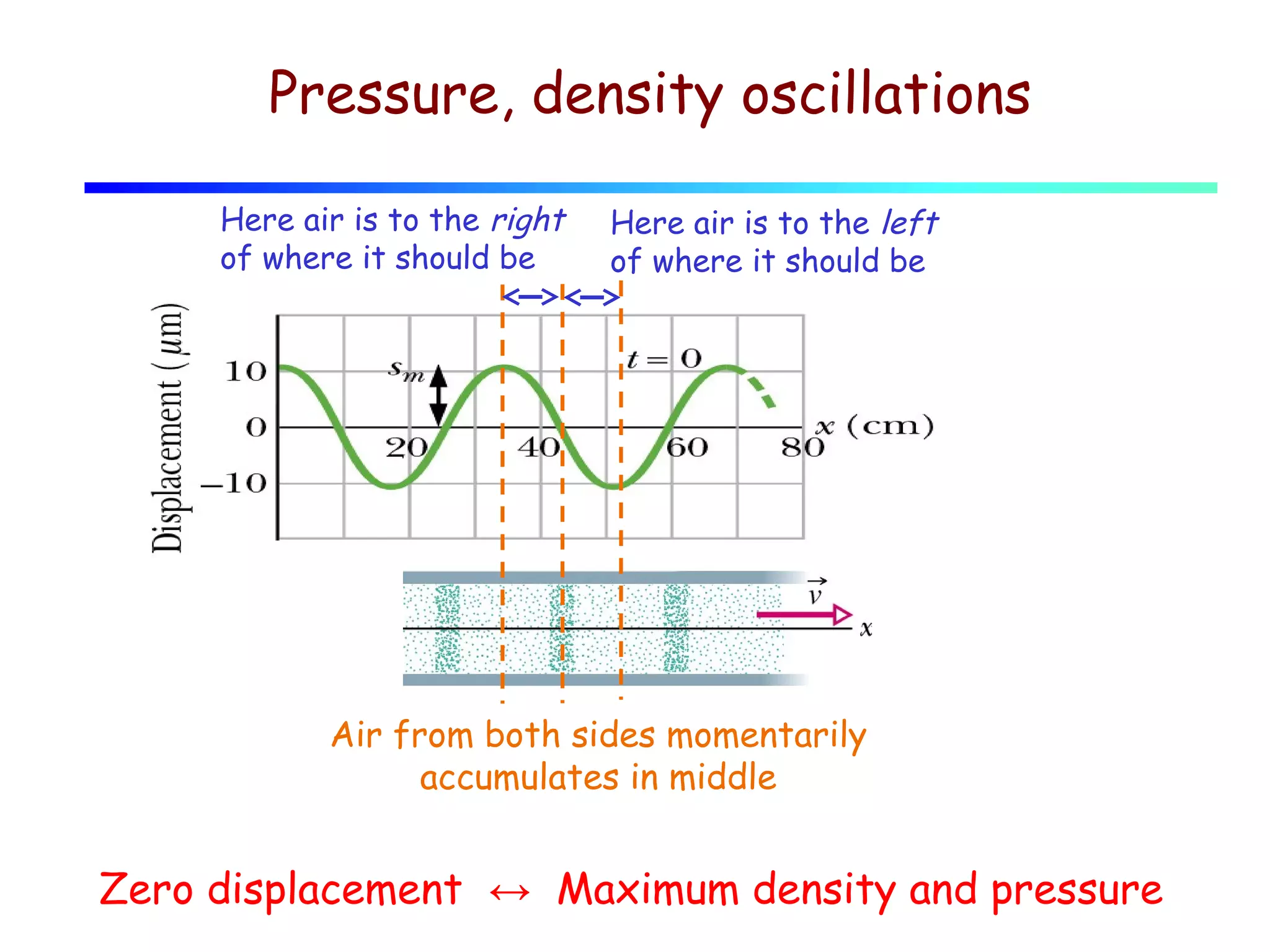
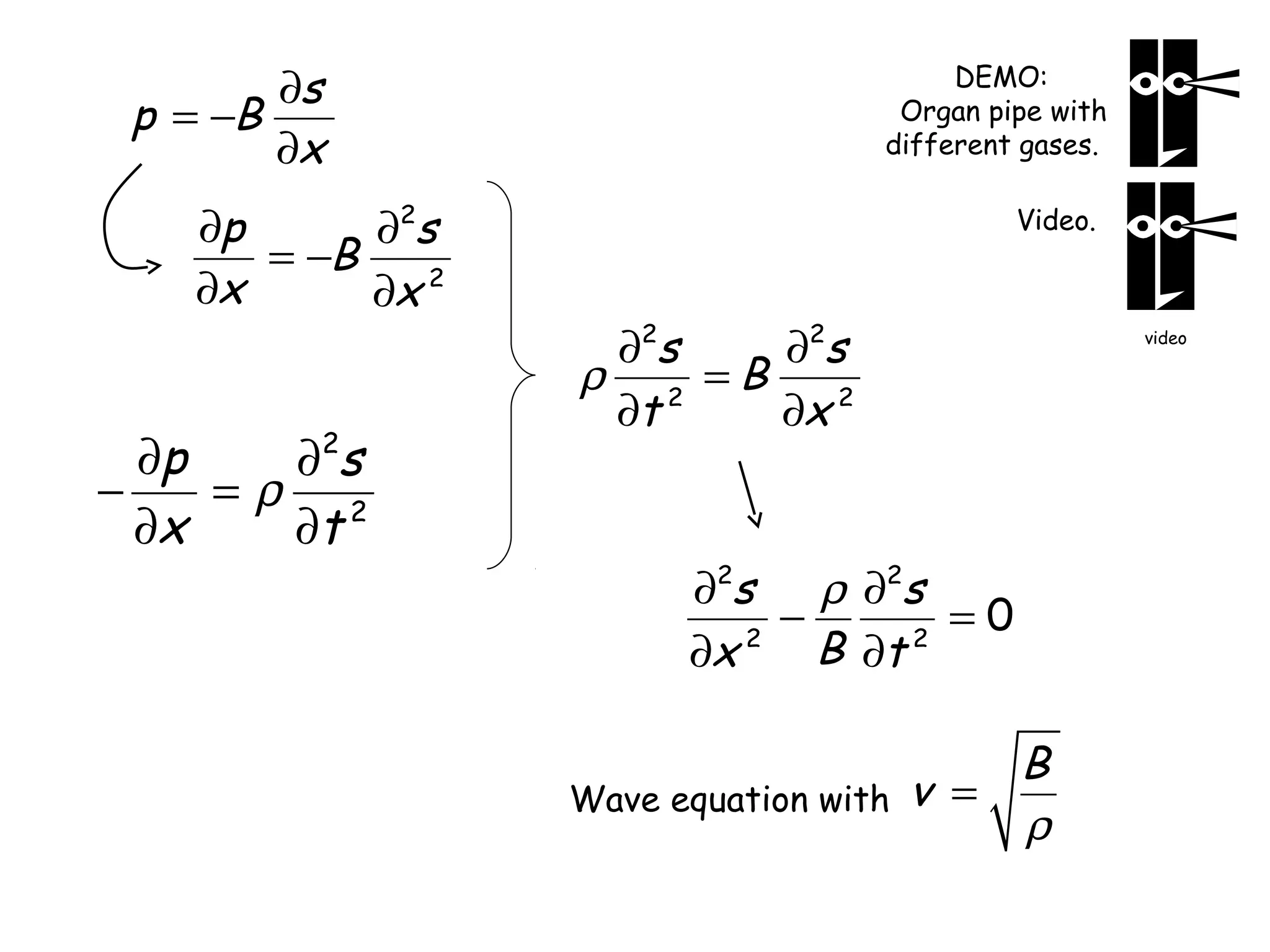
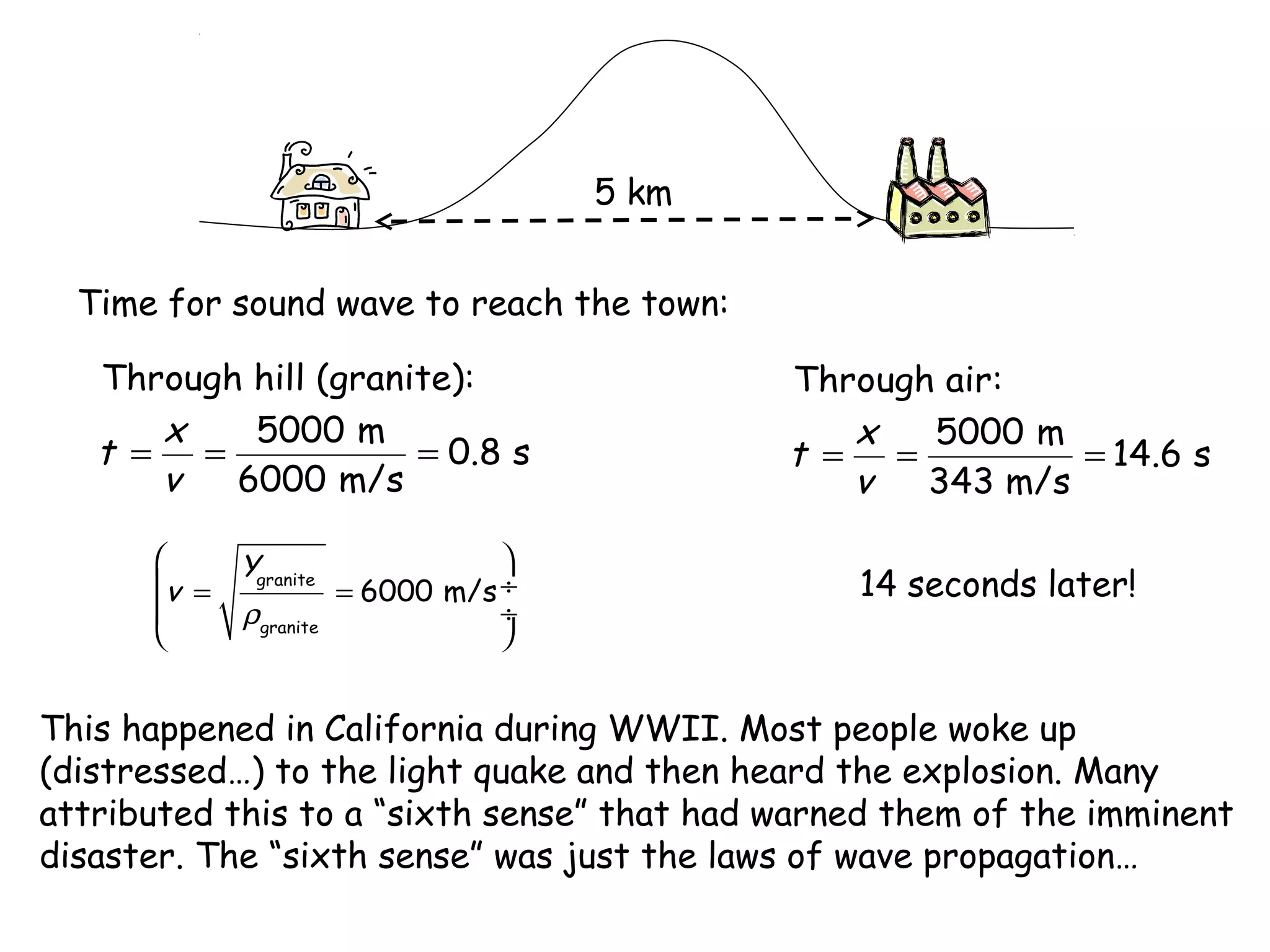
1) Sound waves propagate as periodic longitudinal oscillations of particles in a medium, causing oscillations in pressure and density around the equilibrium values. 2) The speed of sound in a medium depends on its bulk modulus and density, following the equation v = √(B/ρ). 3) Sound intensity decreases with the square of the distance from the source, following the inverse square law. It can be calculated from the sound pressure or particle displacement using equations provided.

1. Lecture 7
Sound waves. Speed of sound.
Intensity.

2. ACT: Dust in front of loudspeaker
Consider a small dust particle, suspended in air (due to buoyancy)
speaker
dust particle
When you turn on the speaker, the dust particle
A. oscillates back and forth horizontally, and moves slowly to the
right
B. steadily moves to the right
C. oscillates back and forth horizontally
DEMO:
Candle

3. Pressure/density oscillations
Gas in equilibrium: pressure and density are uniform.
Sound wave: periodic longitudinal oscillations of particles in
the gas
Consider one slice of air:
1. Oscillation to the right causes pressure to increase
2. Increase in force causes neighboring air to be
displaced
→ sound wave propagates
3. Slice of air oscillates back to region of low pressure
The small volumes of air do not propagate with wave,
they only oscillate around their equilibrium position. DEMO:
Sound in
vacuum.

4. Harmonic longitudinal waves
Consider a gas in long, thin, horizontal tube. Each particle of gas
oscillates horizontally in a harmonic way:
s (x ,t ) = smax cos(kx − ωt )
air normally at x = 0, displaced to right by 10 µm
air normally at x = 50 cm, displaced to left by 10 µm

5. Pressure, density oscillations
Here air is to the right
of where it should be
Here air is to the left
of where it should be
Air from both sides momentarily
accumulates in middle
Zero displacement ↔ Maximum density and pressure

6. Pressure and density oscillations
It all boils down to a phase difference:
Displacement
s (x ,t ) = smax cos(kx − ωt )
Pressure
p (x ,t ) = pmax sin(kx − ωt )
Note that p is the gauge pressure. The pressure of air in equilibrium
is patm. The oscillations give a total pressure ptotal (x ,t ) = patm + p (x ,t )
Density
∆ρ (x ,t ) = ∆ρmax sin(kx − ωt )
Density oscillations are also about the regular air density.
Total density is ρtotal (x ,t ) = ρ0 + ∆ρ (x ,t )

7. Relation between displacement and pressure
Consider a pipe of cross-sectional area A filled with air,
and a small element at x with thickness Δx.
In equilibrium:
p0
x
p0
Δx
Due to a wave, element moves and changes its size
x+s
p0 + p1
p0 + p2
Δx + Δs

8. Pressure and displacement are related through the
bulk modulus of the air!
(gauge pressure)
p
B =−
∆V
V
V = A ∆x
∆V = A ∆s
∆V
∆s
∂s
=

→
∆x →0
V
∆x
∂x
∂s (x ,t )
p (x ,t ) = −B
∂x
The harmonic case:
s (x ,t ) = smax cos(kx − ωt )
→
p (x ,t ) = Bksmax sin(kx − ωt )
pmax

9. Sound wave speed
p0
x
p0
x+s
p0 + p1
Δ x + Δs
Δx
Net force on the element:
Acceleration of the element:
Mass of the element:
∂2s
( p1 − p2 )A = ρA ∆x
∂t 2
( p1 − p2 )
∂2s
=ρ 2
∆x
∂t
p0 + p2
F = ( p1 − p2 )A
∂2s
a = 2
∂t
∆m = ρ A ∆x
∆x → 0
∂p
∂2s
−
=ρ 2
∂x
∂t

10. ∂s
p = −B
∂x
∂p
∂2s
= −B
∂x
∂x 2
∂p
∂2s
−
=ρ 2
∂x
∂t
DEMO:
Organ pipe with
different gases.
Video.
∂2s
∂2s
ρ 2 =B
∂t
∂x 2
video
∂2s
ρ ∂2s
−
=0
2
2
B ∂t
∂x
Wave equation with
B
v =
ρ

11. In-class example: Sonar
A sound wave in water has a frequency of 1000 Hz. What is
its wavelength? (B water = 2.0 GPa, ρ water = 1000 kg/m3)
A.
B.
C.
D.
E.
1.4 mm
0.14 m
14 m
1400 m
None of the above
B
2.0 × 109 Pa
v =
=
= 1414 m/s
3
3
ρ
10 kg/m
λ=
v 1414 m/s
=
= 1.4 m
f
1000 Hz

12. Wave speed, in general
F
String: v =
µ
In general:
Sound in a fluid: v =
restoring force property
v =
inertial property
Sound in a solid:
v =
Y
ρ
B
ρ

13. ACT: A sixth sense?
A large ammunition factory and a town are separated by a rocky
hill, at a horizontal distance of about 5 km. An accident produces a
huge explosion in the middle of the night. What do the town
inhabitants experience?
A. First the room shakes, and then they hear an
explosion.
B. First they hear an explosion, and then the
room shakes.
C. They hear an explosion and the room shakes at
the same time.

14. 5 km
Time for sound wave to reach the town:
Through hill (granite):
x
5000 m
t = =
= 0.8 s
v
6000 m/s

v =


Ygranite
ρgranite

= 6000 m/s ÷
÷

Through air:
x
5000 m
t = =
= 14.6 s
v
343 m/s
14 seconds later!
This happened in California during WWII. Most people woke up
(distressed…) to the light quake and then heard the explosion. Many
attributed this to a “sixth sense” that had warned them of the imminent
disaster. The “sixth sense” was just the laws of wave propagation…

15. Intensity
P
I =
area
Average power (over time) in wave
Area of the surface where this power is distributed
Example: A siren emits a sound of power 2W at 100 m from you.
How much power reaches your ear (eardrum area = 0.7 cm2)
Sphere of
Intensity at distance r from source:
area 4π r 2
r
P
2W
IR = at source =
= 1.6 × 10 −5 W/m2
2
4π r 2
4π ( 100 m )
Power absorbed by eardrum:
(
)(
)
Peardrum = IR × ( area of eardrum ) = 1.6 × 10 −5 W/m2 0.7 × 10 −4 m2 = 1.1 nW

16. Distance and amplitude
At distance r from the source, the power is Pr µ Ir µ
We also know that P µ ( Amplitude )
2
Amplitude decreases as
1
r
1
r2

17. Intensity for harmonic waves
I =
P
=
A
r r
F ×
v
A
=
Fxv x
ds
= p
dt
A
s (x ,t ) = smax cos(kx − ωt )
p (x ,t ) = Bksmax sin(kx − ωt )
I = Bk ωs
2
max
sin (kx − ω )
t
2
=
ds
= smaxω sin(kx − ωt )
dt
1
2
Bk ωsmax
2
B
v =
ρ
Or, in terms of pmax = Bksmax
Useful to include
frequency effects
1
2
I =
ρ B ω 2smax
2
2
pmax
I =
ρB

18. Sound intensity level
β = 10log
I
I0
with I 0 = 10 −12 W/m2
Units: decibels
Threshold of human hearing: 10-12 W/m2
Normal conversation: 10-6 W/m2
Threshold of pain: 1 W/m2
→ β =0
→ β = 65 decibels
→ β = 120 decibels
Twice the decibels does NOT feel twice as loud!